Задача о разделении множества на группы.
Какова вероятность оказаться в одной группе?
Эта задача по комбинаторике и теорверу удостоилась отдельного урока, поскольку тянет на добротный реферат или даже курсовик, ввиду многообразия вариантов. Также она может пригодиться в ваших прикладных исследованиях. Но довольно лирики.
Общая постановка задачи: множество, состоящее из 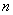 объектов, случайно делится на две, три или бОльшее количество групп. Сколькими способами это можно сделать? Какова вероятность того, что два (три или бОльшее количество) определённых объекта окажутся в одной группе? В разных группах? объектов, случайно делится на две, три или бОльшее количество групп. Сколькими способами это можно сделать? Какова вероятность того, что два (три или бОльшее количество) определённых объекта окажутся в одной группе? В разных группах?
В учебных задачах часто речь идёт о людях, но, конечно же, это могут быть и неодушевлённые предметы.
Задача 1
Класс из 26 человек случайным образом делится на две равные группы. Сколькими способами это можно сделать? Какова вероятность того, что два друга окажутся в одной группе? В разных группах?
И, прежде чем решать, пара важных замечаний.
Во-первых, разделение на группы имеет случайный характер, то есть любая комплектация групп равновозможна и равновероятна. При этом сам алгоритм разбиения значения не имеет – годится любая подходящая жеребьёвка, вплоть до некой псевдослучайности, когда Марьванна указывает перстом на учеников в соответствии со своими бабочками в голове. При этом субъективные факторы (пожелания учеников, пристрастия учителя и т. п.) исключаются.
Во-вторых, группы будем считать РАЗНЫМИ, одна займётся рисованием, другая – лепкой. Назовём их первой группой и второй группой.
Решение данной задачи часто вызывает затруднения, и в таких случаях я рекомендую следующий приём: уменьшить количество объектов и конкретизировать условие. После чего, разобравшись с решением, перенести рассуждения на бОльшее множество.
А посему назовём друзей Петя, Боря и рассмотрим коллектив, состоящий из 4 человек, добавим Аню, Иру.
Очевидно, что в результате разделения у нас получится две группы по два человека в каждой; нетрудно перечислить все возможные варианты:
ПБ АИ
АИ ПБ,
это когда друзья оказались в одной группе, и ещё:
ПА БИ
ПИ БА
БА ПИ
БИ ПА
Итого: 6 возможных вариантов
Заметим, что если не принимать во внимание, какая группа первая, а какая вторая, то варианта будет всего три, но мы договорились считать группы РАЗНЫМИ. Также обращаю внимание, что порядок расположения людей в самих группах значения не имеет, так, если мы возьмём разбиение ПБ АИ и переставим друзей: БП АИ, то это будет считаться той же комбинацией. И это вовсе не занудство. Не всем читателям понятны эти моменты, и к тому же, задачи могут быть разными! Будьте внимательны! Если внутри групп распределяются какие-нибудь роли, то количество вариантов увеличится.
Но вернёмся в основное русло. Поскольку в нашем распоряжении есть все элементарные исходы и они равновозможны (что очень важно), то применИмо классическое определение вероятности:
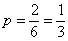 – вероятность того, что друзья окажутся в одной группе; – вероятность того, что друзья окажутся в одной группе;
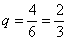 – вероятность того, что они окажутся в разных группах. – вероятность того, что они окажутся в разных группах.
Контроль: 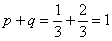 , ч. т. п. , ч. т. п.
Хорошо. Теперь увеличим коллектив до 6 человек, добавим Олю, Юлю, в результате получится две группы по три ученика:
*** ***
В принципе, и здесь не так сложно перечислить все возможные варианты, но давайте уже привлечём на помощь комбинаторику, по формуле количества сочетаний:
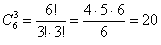 способами можно выбрать трёх человек из шести в первую группу. При этом, очевидно, все возможные варианты разбиения учтены. …Если это не совсем понятно, повторИте, что такое сочетания. способами можно выбрать трёх человек из шести в первую группу. При этом, очевидно, все возможные варианты разбиения учтены. …Если это не совсем понятно, повторИте, что такое сочетания.
Итак, общее число исходов определено, разбираемся с благоприятствующими исходами.
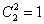 способом можно выбрать друзей в первую группу и способом можно выбрать друзей в первую группу и 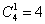 способами – третьего человека. По правилу умножения комбинаций: способами – третьего человека. По правилу умножения комбинаций: 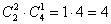 способами можно составить первую группу с Петей и Борей, а именно, это варианты: способами можно составить первую группу с Петей и Борей, а именно, это варианты:
ПБА ИОЮ
ПБИ АОЮ
ПБО АИЮ
ПБЮ АИО
Аналогично проведём рассуждения для второй группы: 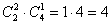 способами можно выбрать друзей и третьего человека во 2-ю группу: способами можно выбрать друзей и третьего человека во 2-ю группу:
ИОЮ ПБА
АОЮ ПБИ
АИЮ ПБО
АИО ПБЮ
Итого: 4 + 4 = 8 случаев, когда Петя и Боря оказываются в одной группе.
По классическому определению вероятности:
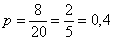 – вероятность того, что друзья окажутся в одной группе. – вероятность того, что друзья окажутся в одной группе.
Вероятность того, что они окажутся в разных группах проще вычислить с помощью теоремы о сумме вероятностей событий, образующих полную группу:
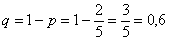
Но, как вариант, можно не полениться продолжить комбинаторные рассуждения:
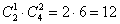 способами можно выбрать одного друга из двух и двух девушек из четырёх в первую группу. А именно, это все возможные варианты первой группы с Петей без Бори: способами можно выбрать одного друга из двух и двух девушек из четырёх в первую группу. А именно, это все возможные варианты первой группы с Петей без Бори:
ПАИ БОЮ
ПАО БИЮ
ПАЮ БИО
ПИО БАЮ
ПИЮ БАО
ПОЮ БАИ
и с Борей без Пети:
БАИ ПОЮ
БАО ПИЮ
БАЮ ПИО
БИО ПАЮ
БИЮ ПАО
БОЮ ПАИ
Итого: 6 + 6 = 12 вариантов.
Таким образом, по классическому определению:
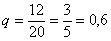
И после сего обстоятельного разбора не составит труда решить задачу для 26 учеников.
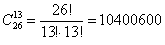 способами выбрать 13 человек из 26, или что фактически то же самое – разделить класс на две равные части. способами выбрать 13 человек из 26, или что фактически то же самое – разделить класс на две равные части.
Для расчёта больших значений можно использовать калькулятор по теорверу или же проявить хитрость и оптимизировать вычисления (см. ниже). Заметим, кстати, ещё одну вещь – комбинаторику не интересует, случайны или не случайны комбинации, она просто констатирует их количество.
Теперь рассчитаем количество благоприятствующих исходов:
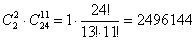 способами можно выбрать 2 друзей и ещё 11 человек (из оставшихся 24) в первую группу. способами можно выбрать 2 друзей и ещё 11 человек (из оставшихся 24) в первую группу.
И такое же количество вариантов для второй группы:
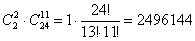
Итого: 2496144 + 2496144 = 4992288.
Таким образом, по классическому определению:
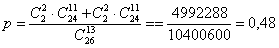 – вероятность того, что два друга окажутся в одной группе. И обещанная техника: – вероятность того, что два друга окажутся в одной группе. И обещанная техника:
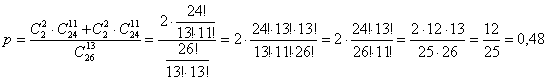
По теореме сложения вероятностей противоположных событий:
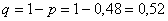 – вероятность того, что друзья окажутся в разных группах. – вероятность того, что друзья окажутся в разных группах.
Ответ: 10400600 способами, 0,48; 0,52
Анализируя решение, напрашивается гипотеза, что с увеличением общего количества учеников, вероятность 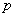 стремится к 0,5. Проверим так ли это. Сначала составим общую формулу для коллектива из чётного количества стремится к 0,5. Проверим так ли это. Сначала составим общую формулу для коллектива из чётного количества 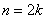 людей: людей:
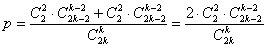 – вероятность того, что два определённых человека окажутся в одной группе. – вероятность того, что два определённых человека окажутся в одной группе.
Распишем сочетания и упростим факториалы:
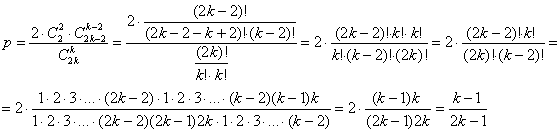
Для самоконтроля подставим рассчитанные в задаче значения 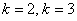 и и 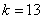 . .
Осталось вычислить простенький предел последовательности при 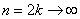 , впрочем, тут всё и так видно: , впрочем, тут всё и так видно:
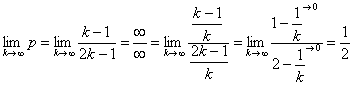
Разумеется, множество объектов можно делить и не на равные группы, принципиально решение не изменится:
Задача 2
Класс из 25 человек случайным образом делится на две группы, 12 и 13 человек.
Вопросы те же, что и в предыдущей задаче.
Решение: найдём общее число исходов:
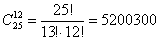 способами можно выбрать 12 человек из 25 (то есть составить две искомые группы). Очевидно, что это количество можно вычислить и «зеркально»: способами можно выбрать 12 человек из 25 (то есть составить две искомые группы). Очевидно, что это количество можно вычислить и «зеркально»:
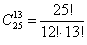
Теперь подсчитаем благоприятствующие исходы:
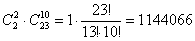 способами можно выбрать двух друзей и ещё 10 человек в группу из 12 человек. способами можно выбрать двух друзей и ещё 10 человек в группу из 12 человек.
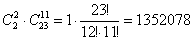 способами можно выбрать двух друзей и ещё 11 человек в группу из 13 человек. способами можно выбрать двух друзей и ещё 11 человек в группу из 13 человек.
Итого: 1144066 + 1352078 = 2496144 способами можно выполнить разделение на группы так, чтобы друзья оказались в одной группе.
По классическому определению вероятности:
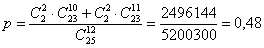 – вероятность того, что два друга окажутся в одной группе. – вероятность того, что два друга окажутся в одной группе.
Найдём противоположную вероятность, и тут можно пойти двумя путями.
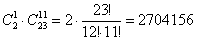 способами можно выбрать одного друга из двух и ещё 11 человек в группу из 12 человек (тем самым учтены все благоприятствующие исходы). способами можно выбрать одного друга из двух и ещё 11 человек в группу из 12 человек (тем самым учтены все благоприятствующие исходы).
По классическому определению:
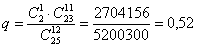 – вероятность того, что друзья окажутся в разных группах. – вероятность того, что друзья окажутся в разных группах.
Либо через сумму вероятностей противоположных событий:
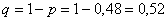
Ответ: 5200300 способами, 0,48; 0,52
Любопытно, что вероятности получились точно такими же, как и при разделении 26 человек на две равные группы!
Задание: вывести общие формулы этих вероятностей для группы, состоящей из нечётного количества 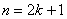 объектов, объектов, 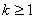 (целое), при их случайном разбиении на две группы численностью (целое), при их случайном разбиении на две группы численностью 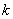 и и 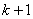 объектов. объектов.
С решением можно свериться в конце урока, на всякий пожарный ещё раз формулы и справка по многоэтажным дробям.
И, конечно, творческое задание, тоже для самостоятельного решения:
Задача 3
В коробке перемешано 5 пар перчаток разных размеров. Катя наугад выбирает пять перчаток. Какова вероятность, что среди них окажется подходящая ей пара 8-го размера? Сколько перчаток нужно выбрать, чтобы эта вероятность превысила 0,5? Была максимальной?
Будьте внимательны ;) Решаем, сверяемся и усложняем задание, впрочем, это ещё не сложность:
Задача 4
Партия из 20 товаров, среди которых три нестандартных, случайным образом делится на две равные части для их отправки на два маркетплейса. Какова вероятность, что на один из маркетплейсов поступят все три нестандартных товара?
Иными словами, здесь нужно вычислить вероятность того, что три определённых объекта окажутся в одной группе и решение напоминает первые задачи:
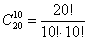 способами можно разделить товары на две равные группы, заметьте, что по условию, это значение можно не считать. способами можно разделить товары на две равные группы, заметьте, что по условию, это значение можно не считать.
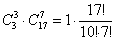 способами можно выбрать 3 нестандартных и 7 других товаров в первую группу. И столькими же способами – во вторую. способами можно выбрать 3 нестандартных и 7 других товаров в первую группу. И столькими же способами – во вторую.
По классическому определению вероятности:
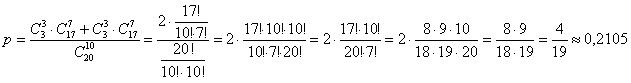 – вероятность того, что на один из маркетплейсов поступят все три нестандартных товара. – вероятность того, что на один из маркетплейсов поступят все три нестандартных товара.
Ответ: 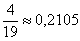
Желающие могут факультативно подсчитать количество других комбинаций, а также вывести предельные формулы вероятностей, когда количество объектов 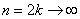 . Трудностей тут никаких, выкладки почти такие же, как в Задаче 1, главное, грамотно разгрести факториалы. Аналогично можно рассчитать вероятности того, что в одной группе окажутся 4, 5 или бОльшее количество определённых объектов. . Трудностей тут никаких, выкладки почти такие же, как в Задаче 1, главное, грамотно разгрести факториалы. Аналогично можно рассчитать вероятности того, что в одной группе окажутся 4, 5 или бОльшее количество определённых объектов.
И, разумеется, множество объектов можно делить и на бОльшее количество частей:
Задача 5
Студенческая группа, состоящая из 18 человек, случайным образом делится на три равные части для выполнения примерно одинаковых по сложности лабораторных работ. Какова вероятность, что у одной из подгрупп будет существенное преимущество перед другими, если в группе 2 отличника? Предположим, Вы «обычный» студент и состоите в данной группе. Какова Ваша вероятность оказаться в «сильной» подгруппе?
Вывести общие формулы вероятностей для группы из 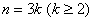 человек. человек.
А вот это уже что-то! Думаем и решаем самостоятельно, используйте «по цепочке» правило умножения комбинаций, по аналогии с Задачей 8 указанного урока.
И, конечно, ещё раз выражаю благодарность за ваши письма! Эта скромная статья появилась как раз благодаря обратной связи. Если у вас есть или появятся какие-то дополнительные выкладки по теме, обязательно пишите! – всем будет интересно. Напоминаю, что есть усложнённая версия задачи, где помимо распределения объектов по группам, им внутри групп присваиваются различные атрибуты / роли.
Желаю творческих и не только успехов!
Решения и ответы:
Задание: 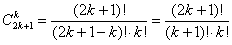 способами можно выполнить разбиение на две группы. способами можно выполнить разбиение на две группы.
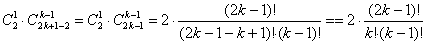 способами можно выполнить разделение на две группы так, чтобы два определённых объекта оказались в разных группах. способами можно выполнить разделение на две группы так, чтобы два определённых объекта оказались в разных группах.
По классическому определению:
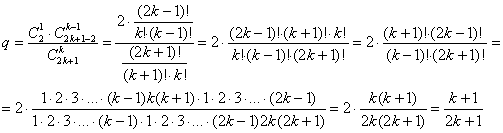
– вероятность того, что два определённых объекта окажутся в разных группах.
По теореме сложения вероятностей противоположных событий:
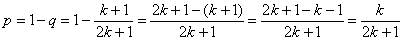 – вероятность того, что они окажутся в одной группе. – вероятность того, что они окажутся в одной группе.
Ответ: 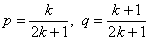
Примечание: нетрудно заметить, что эти вероятности (для нечётного количества объектов 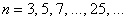 ) совпадают с соответствующими вероятностями для чётного количества объектов: ) совпадают с соответствующими вероятностями для чётного количества объектов: 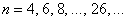 . .
Задача 3. Решение: 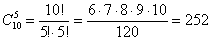 способами можно выбрать 5 перчаток из коробки. способами можно выбрать 5 перчаток из коробки.
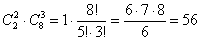 способами можно выбрать две нужные перчатки и три другие. способами можно выбрать две нужные перчатки и три другие.
По классическому определению вероятности:
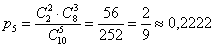 – вероятность того, что среди 5 извлечённых перчаток окажется подходящая пара. – вероятность того, что среди 5 извлечённых перчаток окажется подходящая пара.
! Перчатки, оставшиеся в коробке, по условию, во внимание не принимаются!
Теперь пусть Катя извлекает 6 перчаток, это можно сделать:
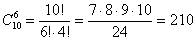 способами. способами.
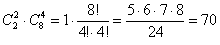 способами можно выбрать нужную пару и 4 другие перчатки. способами можно выбрать нужную пару и 4 другие перчатки.
По классическому определению:
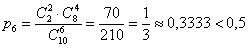
Семь перчаток можно извлечь 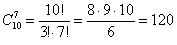 способами. способами.
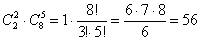 способами можно выбрать нужную пару и 5 других перчаток. способами можно выбрать нужную пару и 5 других перчаток.
По классическому определению, 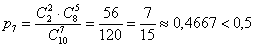 . .
Восемь перчаток можно извлечь 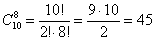 способами. способами.
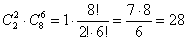 способами можно выбрать нужную пару и 6 других перчаток. способами можно выбрать нужную пару и 6 других перчаток.
По классическому определению, 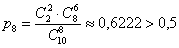 . .
И, очевидно, что эта вероятность будет максимальной (единица), если выбрать все перчатки из коробки.
Ответ: 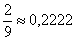 , не менее 8 перчаток, все перчатки. , не менее 8 перчаток, все перчатки.
Задача 5. Решение: по правилу умножения комбинаций:
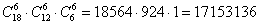 способами можно выбрать 6 человек в первую подгруппу и 6 человек во вторую подгруппу и 6 человек в третью подгруппу. Это произведение учитывает все возможные разбиения группы на 3 равные части – чуть больше 17 млн. вариантов, в принципе, не так уж по меркам комбинаторики и много. способами можно выбрать 6 человек в первую подгруппу и 6 человек во вторую подгруппу и 6 человек в третью подгруппу. Это произведение учитывает все возможные разбиения группы на 3 равные части – чуть больше 17 млн. вариантов, в принципе, не так уж по меркам комбинаторики и много.
Подсчитаем количество благоприятствующих исходов, а именно комбинации, где оба отличника оказываются в одной подгруппе, то есть она получает существенное преимущество перед остальными подгруппами.
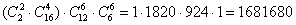 способами можно выбрать 2 отличников и 4 других студентов в первую подгруппу и 6 студентов во вторую подгруппу и 6 студентов в третью подгруппу. Но это ещё не всё. способами можно выбрать 2 отличников и 4 других студентов в первую подгруппу и 6 студентов во вторую подгруппу и 6 студентов в третью подгруппу. Но это ещё не всё.
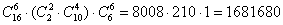 способами можно выбрать 6 неотличников из 16 в первую подгруппу и 2 отличников с 4 неотличниками во вторую подгруппу и 6 неотличиков в третью подгруппу. способами можно выбрать 6 неотличников из 16 в первую подгруппу и 2 отличников с 4 неотличниками во вторую подгруппу и 6 неотличиков в третью подгруппу.
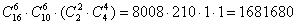 способами можно выбрать 6 неотличников из 16 в первую подгруппу и 6 неотличников и 10 во вторую подгруппу и третью подгруппу с 2 отличниками. способами можно выбрать 6 неотличников из 16 в первую подгруппу и 6 неотличников и 10 во вторую подгруппу и третью подгруппу с 2 отличниками.
Все три значения получись одинаковыми, что неудивительно, ведь подгруппы равноправны. Их можно просуммировать, или, как вариант, утроить первую цепочку благоприятствующих исходов:
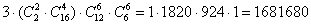 – подразумевая, что на первом месте мы последовательно рассмотрели первую, вторую и третью подгруппы. – подразумевая, что на первом месте мы последовательно рассмотрели первую, вторую и третью подгруппы.
По классическому определению вероятности:
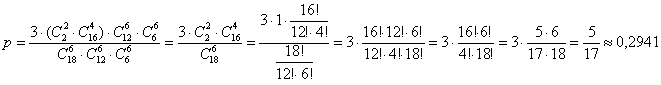 – вероятность того, что одна из подгрупп получит существенное преимущество перед другими. – вероятность того, что одна из подгрупп получит существенное преимущество перед другими.
Контроль: 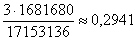 . .
Предположим, Вы неотличник и состоите в данной группе. Найдём вероятность того, что при данном разбиении Вы окажетесь в сильной подгруппе. Эта задача эквивалентна следующей: что три определённых человека (2 отличника и Вы) окажутся в одной подгруппе.
Количество благоприятствующих исходов рассчитывается аналогично:
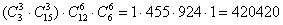 способами можно составить первую подгруппу с вашей тройкой и вторую подгруппу и третью подгруппу. способами можно составить первую подгруппу с вашей тройкой и вторую подгруппу и третью подгруппу.
Такое же количество комбинаций имеет место быть, когда ваша тройка содержится во второй и в третьей подгруппах, а посему рассчитанное значение следует утроить.
По классическому определению:
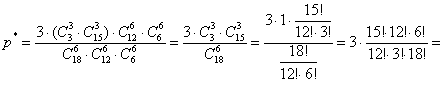
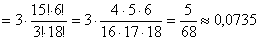 – вероятность того, что Вы окажетесь в сильной подгруппе. – вероятность того, что Вы окажетесь в сильной подгруппе.
Ответ: 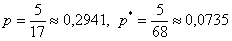 . .
Выведем общие формулы для множества 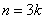 и его разбиения на 3 равные подгруппы: и его разбиения на 3 равные подгруппы:
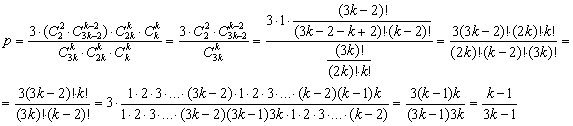
– вероятность того, два определённых человека окажутся в одной подгруппе.
Предельное значение: 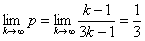
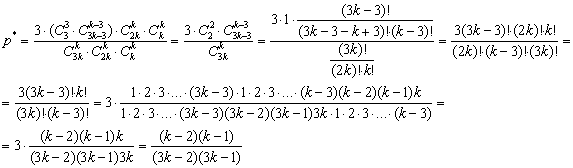
– вероятность того, три определённых человека окажутся в одной подгруппе.
Предельное значение: 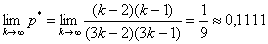
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу сайта)
|

 Высшая математика – просто и доступно!
Высшая математика – просто и доступно! Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net Наш форум, библиотека и блог: mathprofi
Наш форум, библиотека и блог: mathprofi

 Высшая математика – просто и доступно!
Высшая математика – просто и доступно! Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net Наш форум, библиотека и блог: mathprofi
Наш форум, библиотека и блог: mathprofi