


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Ряды динамики для всех
Данную тему можно отнести к статистике, причём не только математической, но дело даже не в этом. Она имеет общеобразовательный характер – вещи, о которых пойдёт речь, должен знать любой грамотный человек – от «чайника» до «самовара». У всех на слуху такие термины, как абсолютный прирост, темп роста, темп прироста и некоторые другие, однако далеко не все чётко представляют, что они обозначают. И сегодня мы не только разберёмся во всей этой кухне раз и навсегда, но и научимся быстро выполнять расчёты, в частности, в Экселе. Давно вам хотел об этом рассказать, и вот час настал…
Начнём с ключевого понятия, которое вы видите в заголовке:
ряд динамики, или что то же самое, временнОй ряд, динамический ряд – это хронологическая последовательность числовых значений некоторого показателя.
Существуют и другие определения, но, в силу специальности, версия у меня получилась математической :) И в лучших традициях проекта немедленный пример, с молочного комбината:

…Чтобы задача была актуальна во все времена и для всех стран, я использовал «денежные единицы».
Итак, перед нами показатель «Выручка от реализации мороженого» и его числовые значения за 6 месяцев, расположенные в хронологическом порядке (от самого раннего значения, последовательно – до самого позднего). Очевидно, что ряд динамики характеризует изменение выручки (в данном примере) во времени: к началу летнего сезона она возрастает, затем достегает некоторого плато и в сентябре существенно падает, что совершенно логично.
Числовые значения называют уровнями ряда и обычно обозначают «игреками» с подстрочными индексами:
![]() .
.
Это даже можно назвать неким неформальным стандартом. Как вариант, можно начать с нулевого индекса, но тогда нижеследующие формулы несколько изменятся. Кстати, в источниках, которые я видел в Сети, есть неточности и ошибки, связанные как раз с индексацией, будьте внимательны.
Каждому уровню ряда соответствует свой временнОй промежуток, это могут быть секунды, минуты, часы, дни, месяцы, кварталы, годы и иже с ними экзотика. Чаще всего временнЫе промежутки ряда одинаковы по продолжительности, как в нашем примере, и такие ряды называют регулярными.
Но это вовсе не обязательное условие. Так, нам могут быть известны данные, скажем, только за апрель, август и сентябрь – и такой набор тоже будет считаться рядом динамики, только нерегулярным. По той причине, что такие ряды, как правило, используют для анализа нерегулярных и зачастую непредсказуемых событий, а-ля вулкан выпустил 2 тонны пепла, через семь месяцев – 5 тонн, а ещё через пару лет – 3 тонны.
В учебной и научной практике, по возможности, конечно же, используют регулярные ряды ввиду их бОльшей и информативности и простоты исследования.
Далее. Ряды динамики бывают интервальными и моментными. В интервальном ряде каждый уровень относятся сразу ко всему соответствующему временнОму промежутку. Как в таблице выше: выручка от реализации мороженого составила ![]() ден. ед. – суммарно за весь апрель,
ден. ед. – суммарно за весь апрель, ![]() – суммарно за весь май и так далее.
– суммарно за весь май и так далее.
В моментном ряду числовые данные (уровни) относятся к последовательным моментам времени, чаще всего это значения показателя на начало либо конец временнОго промежутка. Можно сказать, классический пример – численность сотрудников того же комбината:

…То бишь это данные на начало года, и чтобы задача оставалась молодой, я опять не указал конкретные годы :)
Выбор интервального или моментного ряда во многом зависит от показателя, который мы исследуем. Если сложение уровней имеет содержательный смысл, то используют интервальный ряд, так, если просуммировать выручку за 6 месяцев, то мы получим её значение за полгода, и это весьма полезная информация. Однако нет никакого смысла суммировать сотрудников, скажем, за 5 лет; и для такого рода показателей уместен моментный ряд. Но это не является каким-то незыблемым правилом.
И, тавтологично у меня получилось, зато кратко – переходим к рассмотрению показателей самого ряда динамики. Их можно разделить на три большие группы: средние, базисные и цепные.
Что касаемо средних показателей, то сразу напрашивается вычислить среднее значение ряда. В случае с регулярным интервальным рядом – это простая средняя арифметическая:
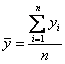 , где
, где ![]() – количество уровней, и на всякий пожарный, вдруг кто ещё не знает – загогулина наверху обозначает свёрнутую запись суммы, где переменная «и» играет роль своеобразного счётчика, изменяясь от 1 до «эн»:
– количество уровней, и на всякий пожарный, вдруг кто ещё не знает – загогулина наверху обозначает свёрнутую запись суммы, где переменная «и» играет роль своеобразного счётчика, изменяясь от 1 до «эн»:
![]()
Вычислим среднемесячную выручку от продажи мороженого:
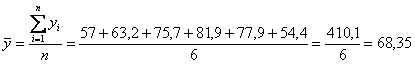 ден. ед. в среднем за месяц.
ден. ед. в среднем за месяц.
Тут всё просто. А вот у моментного ряда есть особенности. Во-первых, мы располагаем лишь моментными данными, так, в примере с сотрудниками их численность зафиксирована лишь на начало каждого года, а вот о том, как она менялась в течение года – информации нет. И во-вторых, фактически нам известны данные за ![]() временнЫх промежутков – последнее значение
временнЫх промежутков – последнее значение ![]() зафиксировано на начало 11-года, но мы ничего не знаем о количестве сотрудников в течение этого года.
зафиксировано на начало 11-года, но мы ничего не знаем о количестве сотрудников в течение этого года.
В такой ситуации используют простую среднюю хронологическую. Суть состоит в том, что за среднее значение 1-го временнОго промежутка (в нашем примере года) принимают ![]() , за среднее значение 2-го промежутка:
, за среднее значение 2-го промежутка: ![]() , за среднее значение 3-го промежутка:
, за среднее значение 3-го промежутка: ![]() , … и так далее, и за среднее значение последнего промежутка:
, … и так далее, и за среднее значение последнего промежутка: ![]() . Затем находят среднее этих значений
. Затем находят среднее этих значений
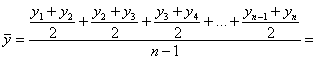
и, упрощая, получаем формулу средней хронологической:
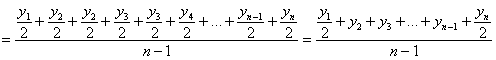
В нашем примере:
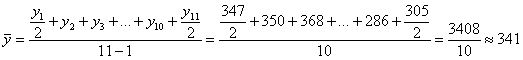 – среднегодовая численность сотрудников комбината. Округляйте, к слову, численность людей до целого человека :)
– среднегодовая численность сотрудников комбината. Округляйте, к слову, численность людей до целого человека :)
В случае неравных по величине временнЫх промежутков используют взвешенные средние, но в реальной практике – это редкость; как правило, используют регулярные ряды (с равными промежутками), поэтому в рамках настоящего урока я опущу соответствующие формулы.
И пришло время зарядить солидную задачу:
Пример 1
Известны следующие данные о деятельности молочного комбината:

Вычислить:
1) Среднюю выручку за 6 месяцев.
2) Базисные абсолютные приросты, темпы роста, темпы прироста.
3) Цепные абсолютные приросты, темпы роста, темпы прироста, и заодно, конечно, коэффициенты роста и прироста.
Абсолютные значения 1% прироста.
Средний абсолютный прирост.
Средний темп роста и средний темп прироста.
…Вроде ничего не забыл, но если что, добавлю.
Решаем, и пункт 1) уже в кармане, коль скоро ряд интервальный, то среднемесячная выручка составляет: 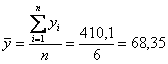 ден. ед.
ден. ед.
2) Показатели базисные. Здесь для анализа ряда выбирают фиксированную базу сравнения – чаще всего это 1-й уровень (далее по умолчанию). Проще говоря, все майские и последующие данные мы будем сравнивать с апрелем месяцем.
Абсолютный прирост базисный – это разность между данным уровнем и уровнем базисным: ![]() , начиная с
, начиная с ![]() .
.
Не пугаемся формул, тут всё просто:
![]() – разность между 2-м и 1-м уровнем, то есть в мае выручка увеличилась на 6,2 ден. ед. по отношению к апрелю;
– разность между 2-м и 1-м уровнем, то есть в мае выручка увеличилась на 6,2 ден. ед. по отношению к апрелю;
![]() – разность между 3-м и 1-м уровнем, то есть в июне выручка увеличилась на 18,7 ден. ед. по отношению к апрелю,
– разность между 3-м и 1-м уровнем, то есть в июне выручка увеличилась на 18,7 ден. ед. по отношению к апрелю,
и более кратко:
на ![]() ден. ед. увеличилась выручка в июле по отношению к апрелю;
ден. ед. увеличилась выручка в июле по отношению к апрелю;
на ![]() ден. ед. увеличилась выручка в августе по отношению к апрелю и, наконец, в сентябре, выручка уменьшилась на
ден. ед. увеличилась выручка в августе по отношению к апрелю и, наконец, в сентябре, выручка уменьшилась на ![]() ден. ед. по отношению к тому же апрелю.
ден. ед. по отношению к тому же апрелю.
Вычисления проводят на калькуляторе, а ещё удобнее – в Экселе, а результаты оформляют таблицей. Можно «горизонтально», можно «вертикально», лично я привык использовать второй вариант:
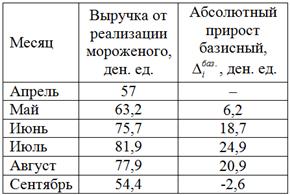
Справа вверху ставим прочерк, поскольку данные за март и соответствующий абсолютный прирост нам не известны. Иногда там рисуют ноль, и это, разумеется, грубая ошибка.
Теперь хочется выяснить, во сколько раз изменились майские и последующие значения выручки по отношению к апрелю. Это можно вычислить в разах и в процентах.
Коэффициент роста базисный – это отношение данного уровня к уровню базисному: ![]() , начиная с
, начиная с ![]() .
.
Темп рост базисный – это сей коэффициент, выраженный в процентах:
![]()
И не отходя от кассы считаем:
![]() , то есть в мае выручка увеличилась примерно в 1,1088 раз по отношению к апрелю. Или эквивалентно – составила:
, то есть в мае выручка увеличилась примерно в 1,1088 раз по отношению к апрелю. Или эквивалентно – составила: ![]() – от апрельского значения.
– от апрельского значения.
Очевидно, что при ![]() речь идёт об уменьшении, а при
речь идёт об уменьшении, а при ![]() – о неизменности, в данном примере выручки. Но последний случай на практике крайне редок.
– о неизменности, в данном примере выручки. Но последний случай на практике крайне редок.
И «родственные» показатели: коэффициент прироста базисный – это отношение абсолютного базисного прироста к базисному уровню, формулу сразу преобразуем:
![]() , то есть для нахождения коэффициента прироста достаточно вычесть единицу из коэффициента роста.
, то есть для нахождения коэффициента прироста достаточно вычесть единицу из коэффициента роста.
И, соответственно, темп прироста базисный – это оный коэффициент в процентах:
![]()
Продолжаем расчёты, коэффициент прироста:
![]() – это означает что абсолютный прирост
– это означает что абсолютный прирост ![]() выручки в мае по отношению к апрелю, составляет примерно 0,1088 от базисного уровня
выручки в мае по отношению к апрелю, составляет примерно 0,1088 от базисного уровня ![]() .
.
Или в другой формулировке, через темп прироста:
![]() – то есть выручка в мае увеличилась примерно на 10,88% по сравнению с апрелем.
– то есть выручка в мае увеличилась примерно на 10,88% по сравнению с апрелем.
! Ещё раз внимательно, не спеша прочитайте и осмыслите эти показатели! И ещё должен сказать, что с обозначениями в нашей теме бардак – кто во что горазд, зачастую используют навороченные индексы наподобие «рб» (рост базисный), «пр. баз.» (прирост базисный), что сильно затрудняет восприятие формул. Я остановился на компромиссном варианте, не отступив в то же самое время от стандартных букв ![]() (коэффициент) и
(коэффициент) и ![]() (темп).
(темп).
Для закрепления распишем ещё один период:
![]() , то есть в июне выручка увеличилась примерно в 1,3281 раз по отношению к апрелю. И сразу в процентах:
, то есть в июне выручка увеличилась примерно в 1,3281 раз по отношению к апрелю. И сразу в процентах:
![]()
Соответственно, темп прироста: ![]() – на столько процентов выросла выручка в июне относительно апреля.
– на столько процентов выросла выручка в июне относительно апреля.
В большинстве задач используют процентные показатели (темпы), и мы продолжаем заполнять таблицу, выполняя вычисления на калькуляторе или, например, в Экселе:
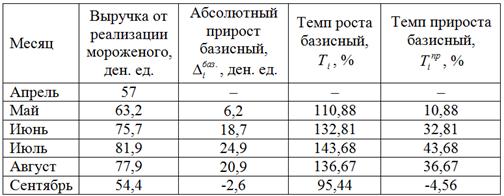
Заметьте, что в сентябре прирост выручки отрицателен: -2,6 ден. ед., что составляет ![]() относительно апрельского значения.
относительно апрельского значения.
И технический стандарт: коэффициенты принято округлять до 4 знаков после запятой, а проценты, соответственно, до 2.
Чуть позже мы посмотрим кино, как быстро выполнить вычисления в Экселе, ну а сейчас переходим к 3-му пункту, где помимо цепных, будут ещё некоторые средние показатели.
3) И, наверное, вы уже догадались, что здесь к чему. Здесь каждый последующий уровень сравнивается с предыдущим.
Так, цепной абсолютный прирост выражается формулой ![]() , начиная с
, начиная с ![]() .
.
Не позволяй душе лениться:
на ![]() ден. ед. увеличилась выручка в мае относительно апреля;
ден. ед. увеличилась выручка в мае относительно апреля;
на ![]() ден. ед. увеличилась выручка в июне относительно мая;
ден. ед. увеличилась выручка в июне относительно мая;
и давайте без протокола:
на ![]() ден. ед. увеличилась выручка в июле относительно июня;
ден. ед. увеличилась выручка в июле относительно июня;
на ![]() ден. ед. уменьшилась выручка в августе относительно июля;
ден. ед. уменьшилась выручка в августе относительно июля;
и на ![]() ден. ед. уменьшилась выручка в сентябре относительно августа.
ден. ед. уменьшилась выручка в сентябре относительно августа.
Начинаем заполнять новую таблицу:
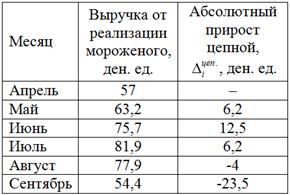
После чего напрашивается вычислить средний абсолютный прирост – это есть сумма цепных приростов, делённая на их количество:
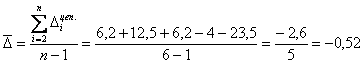 ден. ед. в среднем за один месяц. Вот такой вот несколько неожиданный результат. Что называется, «средняя температура по палате».
ден. ед. в среднем за один месяц. Вот такой вот несколько неожиданный результат. Что называется, «средняя температура по палате».
Сумма цепных приростов – это есть в точности базисный прирост за весь период:
![]() , поэтому средний абсолютный прирост можно вычислить другим способом:
, поэтому средний абсолютный прирост можно вычислить другим способом:
![]()
То есть этот показатель мы могли рассчитать ещё в предыдущем пункте, но тогда мне «на пальцах» пришлось бы объяснять, что это средняя цепных приростов. А тут всё получилось к месту.
Едем дальше. Коэффициент роста цепной – это отношение последующего уровня ряда к предыдущему:
![]() , начиная с
, начиная с ![]() , а если это отношение выражено в процентах, то получаем цепной темп роста:
, а если это отношение выражено в процентах, то получаем цепной темп роста:
![]()
И, наконец, коэффициент и темп прироста цепные – это отношение абсолютного цепного прироста к соответствующему предыдущему уровню, в разах (коэффициент) и в процентах (темп):
![]()
![]() , или, что то же самое:
, или, что то же самое: ![]()
…Всё-таки пришлось мне использовать индекс «прц» – прирост цепной, хотелось использовать другие буквы, но получился бы нестандарт.
И, наверное, вы подметили, что начальные цепные показатели совпадают с соответствующими базисными показателями, которые мы уже рассчитали в предыдущем пункте:
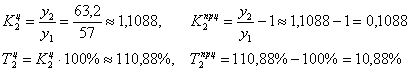
Это сравнение мая с апрелем. Выводы копипастить не буду (см. п. 2), но, конечно же, суть повторим, сравнивая уже июнь с маем:
![]()
То есть выручка в июне увеличилась примерно в 1,1978 раз относительно мая; или – июньское значение (75,7 ден. ед.) составило примерно 119,78% от майского (63,2 ден. ед.).
![]()
То есть абсолютный цепной прирост выручки в июне ![]() – составляет примерно 0,1978 от майского значения (63,2 ден. ед.). Или в темпах, что звучит понятнее: в июне выручка увеличилась примерно на 19,78% относительно мая.
– составляет примерно 0,1978 от майского значения (63,2 ден. ед.). Или в темпах, что звучит понятнее: в июне выручка увеличилась примерно на 19,78% относительно мая.
! Внимательно всё перечитайте и осознайте!
Аналогично считаем дальнейшие цепные значения, результаты заносим в таблицу. Повторюсь, что в большинстве задач требуется рассчитать темпы, но в «цепном» случае полезно добавить и коэффициенты ![]() :
:
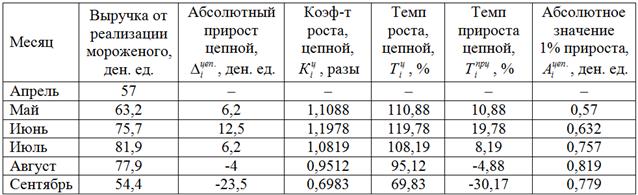
И в правой колонке я рассчитал ещё один показатель: абсолютное значение 1% прироста – это отношение абсолютного цепного прироста к соответствующему темпу прироста: ![]() – он показывает, сколько единиц (в данном примере денежных) содержится в одном проценте прироста.
– он показывает, сколько единиц (в данном примере денежных) содержится в одном проценте прироста.
Так, ![]() – то есть в одном проценте майского прироста содержится 0,57 ден. ед.;
– то есть в одном проценте майского прироста содержится 0,57 ден. ед.;
Примечание: при машинном расчёте мы берём точное значение темпа прироста и всегда получаем точное значение 1% прироста. Причина этого факта обоснована буквально через абзац.
![]() – то есть в одном проценте июньского прироста (по отношению к маю) содержится 0,632 ден. ед., и так далее.
– то есть в одном проценте июньского прироста (по отношению к маю) содержится 0,632 ден. ед., и так далее.
Абсолютное значение 1% прироста – это в точности, предыдущий уровень, делённый на 100: ![]() – взглянИте на выручку и на правую колонку в таблице выше.
– взглянИте на выручку и на правую колонку в таблице выше.
И логика тут простА: возьмём, например, майское значение 63,2 ден. ед., один процент от которого, очевидно, составляет 0,632 ден. ед. И коль скоро в июне сравнение идёт с маем, то июньский прирост +12,5 ден. ед. мы «меряем» как раз в этих «майских» процентах: ![]() – в июне по отношению к маю.
– в июне по отношению к маю.
Следует добавить, что для базисных приростов (см. пункт 2) абсолютное значение 1% прироста – есть величина постоянная, равная 1-му уровню ряда, делённому на 100:
![]() , поскольку каждый базисный прирост мы сравниваем с постоянной базой, апрельскими данными в нашем примере.
, поскольку каждый базисный прирост мы сравниваем с постоянной базой, апрельскими данными в нашем примере.
Но довольно лирики, рассчитаем ещё пару важных показателей.
Средний коэффициент роста – это есть среднее геометрическое цепных темпов роста:
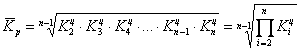 – это показатель, характеризующий, во сколько раз в среднем составило изменение выручки (в нашем примере).
– это показатель, характеризующий, во сколько раз в среднем составило изменение выручки (в нашем примере).
Справка: значок ![]() означает свёрнутую запись произведения, по аналогии с
означает свёрнутую запись произведения, по аналогии с ![]()
Считаем, и вот тут как раз и пригодился столбец с коэффициентами роста:
![]() – то есть в среднем за месяц выручка… уменьшалась в 0,9907 раз. И в данном случае этот показатель не слишком информативен, так как учитывает «провальный» сентябрь. Для анализа сезонного роста выручки осенний месяц целесообразно исключить из рассмотрения.
– то есть в среднем за месяц выручка… уменьшалась в 0,9907 раз. И в данном случае этот показатель не слишком информативен, так как учитывает «провальный» сентябрь. Для анализа сезонного роста выручки осенний месяц целесообразно исключить из рассмотрения.
Средний темп роста – это сей коэффициент, выраженный в процентах:
![]()
Средний коэффициент роста можно вычислить и другим способом, не рассчитывая цепные коэффициенты:
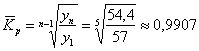
И сопоставляя формулы, легко видеть, что произведение всех цепных коэффициентов – это есть базисный коэффициент роста за весь период:
![]()
Продолжаем, средний коэффициент прироста:
![]()
и средний темп прироста:
![]() , то есть в среднем за месяц убыль выручки составляла около одного процента.
, то есть в среднем за месяц убыль выручки составляла около одного процента.
В подобных задачах почти всегда требуется сделать содержательные выводы, причём в письменной форме. И простенькая аналитика примерно такова: в течение апреля-августа произошёл существенный сезонный рост выручки, при этом максимальный прирост наблюдался в июне: +12,5 ден. ед., что составило +19,78% от майского показателя. В сентябре произошло резкое падение выручки -23,5 ден. ед. и -30,17% соответственно – от августовского значения. За счёт такого уменьшения средние показатели составили ![]() , то есть в среднем за месяц выручка уменьшалась в 0,9907 раз, что составляет
, то есть в среднем за месяц выручка уменьшалась в 0,9907 раз, что составляет ![]() .
.
То есть нужно отметить тенденцию (убывание / рост), её интенсивность; возможные причины (в содержательном плане) максимальные и минимальные значения (приросты), а также средние значения.
Это вам краткий «скелет» для выполнения сего задания. Ну а сейчас смотрим фильм о том, как это всё быстро рассчитать (если видео недоступно, копия тут)::
Следующие задачи для самостоятельного решения, и чтобы вы их-таки порешали, давайте что-нибудь творческое. История о том, как Винни-Пух спасся от наводнения, продолжаем сладкую тему:
Пример 2
Когда все спасательные операции были окончены, на ветке сидел Пух, болтая ногами, а рядом стояло десять горшков с мёдом. На другой день на ветке сидел Пух, болтая ногами, а рядом стояло четыре горшка с мёдом. На третий день на ветке сидел Пух, болтая ногами, а рядом стоял один горшок с мёдом. На четвёртый день на ветке сидел Пух один-одинёшенек.
Требуется:
1) Составить ряд динамики, полагая, что информация о количестве горшков мёда фиксировалась в одно и то же время – на начало дня.
2) Вычислить среднее значение ряда.
3) Вычислить базисные показатели: абсолютные приросты, темпы роста и темпы прироста; абсолютное значение 1% прироста (что оно означает?).
4) Вычислить средний абсолютный прирост, средний коэффициент, темп роста и темп прироста; пояснить смысл найденных значений.
И чтобы вы не «поплыли», сразу заметим, что формула 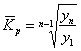 тут не годится, хотя бы по той причине, что
тут не годится, хотя бы по той причине, что ![]() и полученный результат явно не соответствует действительности. И здесь я предлагаю видоизменить формулу: вместо
и полученный результат явно не соответствует действительности. И здесь я предлагаю видоизменить формулу: вместо ![]() взять среднее значение последних двух уровней, а вместо
взять среднее значение последних двух уровней, а вместо ![]() – среднее значение первых двух уровней. И, поскольку ряд моментный (по сути три полных дня), то корень следует извлечь
– среднее значение первых двух уровней. И, поскольку ряд моментный (по сути три полных дня), то корень следует извлечь ![]() степени. Возможно, профессиональные статистики меня поправят (буду рад отзывам), но это выглядит и интерпретируется логично; в «массовых» источниках я не нашел информации по данному вопросу.
степени. Возможно, профессиональные статистики меня поправят (буду рад отзывам), но это выглядит и интерпретируется логично; в «массовых» источниках я не нашел информации по данному вопросу.
5) Сделать краткие выводы.
Чисел тут немного – и решать можно прямо на бумажке :) Пользуясь осязаемым калькулятором. Если всё это, конечно, под рукой. Как вариант, можно использовать Эксель (ссылка для самых ленивых), где я уже оформил «шапку» таблицы.
И ещё одна задача, можно сказать ребус, довольно популярный в учебной практике:
Пример 3
По данным об объеме выпуска продукции на заводе, рассчитайте отсутствующие в таблице сведения:
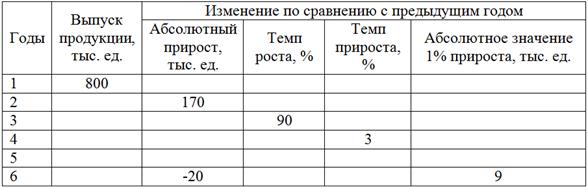
…Данных за 5-й год нет, это не опечатка. Известные значения уже забиты в Эксель, считаем. По ходу заполнения строк сверяйте уровни ряда и абсолютные значения 1% прироста, которые связаны отношением ![]() . После заполнения таблицы также можно скопировать в сторонке значения выпуска продукции и провести «прямые» вычисления по образцу Примера 1. Затем сверить таблицы – они должны совпасть. Это для тех, кто хочет потренироваться.
. После заполнения таблицы также можно скопировать в сторонке значения выпуска продукции и провести «прямые» вычисления по образцу Примера 1. Затем сверить таблицы – они должны совпасть. Это для тех, кто хочет потренироваться.
Определить средние значения показателей: выпуск продукции, абсолютный прирост, темп роста и прироста. Сделать выводы.
Примерный образец оформления задания внизу страницы.
Что ещё интересного по теме?
Уровнями ряда могут выступать не только абсолютные, но и средние, а также относительные значения. Во всех примерах урока фигурировали абсолютные значения, приведу один из них:

Но ведь характер данных может быть и другим:

Здесь уровнями выступают средние за год значения, и такой ряд, очевидно, следует считать интервальным, а не моментным.
Будьте внимательны! – всегда смотрИте, ЧТО вам предложено в условии.
Кроме того, уровни ряда могут представлять собой относительные показатели, например, темпы роста, «классический» пример:
![]()
Переводя с научного на обывательский, речь идёт о бытовой инфляции, и она сама по себе выражается темпом роста. Так, значение 112,55 означает, что во 2-м году цены на потребительские товары и услуги в среднем выросли на 12,55% по отношению к 1-му году.
И для подобных рядов можно рассчитать те же самые показатели, только со своей содержательной спецификой. Например, среднее за 11 лет количество сотрудников (средняя от средних значений). Или темпы роста ИПЦ (темпы роста темпов роста) – они нам говорят об ускорении или замедлении инфляции. И так далее, с вычислениями и интерпретацией результатов – никаких проблем.
Сверяемся с решениями, и пОмните, что сахар вреден:
Надеюсь, этот урок был полезен и он, конечно, не единственный по теме – переходим к сглаживанию временнЫх рядов.
Пример 2. Решение: 1) Составим ряд динамики:

2) Вычислим среднее значение. Поскольку ряд моментный, используем среднюю хронологическую:
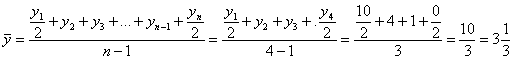 – среднедневное количество горшков с мёдом.
– среднедневное количество горшков с мёдом.
3) Вычислим базисные показатели, абсолютные приросты по формуле ![]() , начиная с
, начиная с ![]() , темпы роста по формуле
, темпы роста по формуле ![]() и темпы прироста по формуле
и темпы прироста по формуле ![]() . Результаты сведём в таблицу:
. Результаты сведём в таблицу:
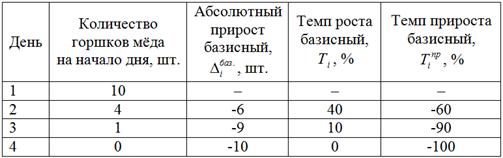
Вычислим абсолютное значение 1% прироста. Так как база сравнения ![]() постоянная, то:
постоянная, то: ![]() горшка содержится в 1% прироста (см. правый столбец). Например, во 2-й день:
горшка содержится в 1% прироста (см. правый столбец). Например, во 2-й день: ![]() горшков (абсолютный прирост), и аналогично в последующие дни.
горшков (абсолютный прирост), и аналогично в последующие дни.
4) Вычислим средний абсолютный прирост:
![]() горшка – съедал Винни-Пух в среднем за день.
горшка – съедал Винни-Пух в среднем за день.
Вычислим средний коэффициент роста, для этого найдём среднее значение первых двух уровней: ![]() и двух последних:
и двух последних: ![]() . Поскольку ряд моментный, то
. Поскольку ряд моментный, то
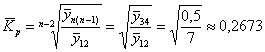
Средний темп роста:
![]() – то есть на каждый следующий день мёда оставалось в среднем 26,73% от значения предыдущего дня.
– то есть на каждый следующий день мёда оставалось в среднем 26,73% от значения предыдущего дня.
Средний темп прироста:
![]() – среднедневная убыль мёда.
– среднедневная убыль мёда.
Примечание: и это похоже на правду: если подсчитать цепные темпы прироста (что легко сделать устно), то в 1-й день Пух съел 60% мёда, во 2-й – 75% (3 горшка из 4) и в 3-й – 100% (последний горшок).
Примечание 2: средний абсолютный прирост можно рассчитать альтернативно, практически с тем же результатом: ![]() горшка.
горшка.
5) Краткие выводы: большую часть мёда, 6 горшков, Винни-Пух съел в 1-й день, что составило 60% от всех запасов, а во 2-й день – ещё три горшка, из чего следует, что Пух очень любит мёд и не может удержаться от его чрезмерного потребления, даже в экстремальных условиях. Среднедневная убыль составила ![]() горшка, а интенсивность поглощения примерно
горшка, а интенсивность поглощения примерно ![]() – в среднем за день.
– в среднем за день.
Пример 3. Решение: приступаем к заполнению таблицы.
1) Прежде всего, ставим прочерки в пустых ячейках 1-го года, что означает отсутствие данных.
2) Пользуясь формулой ![]() , находим 2-й уровень ряда:
, находим 2-й уровень ряда:
![]() тыс. ед., после чего рассчитываем недостающие показатели 2-го года:
тыс. ед., после чего рассчитываем недостающие показатели 2-го года:
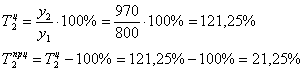
![]() тыс. ед. на 1%
тыс. ед. на 1%
Контроль: ![]()
3) С помощью формулы ![]() найдём 3-й уровень ряда:
найдём 3-й уровень ряда:
![]() тыс. ед.
тыс. ед.
Вычислим остальные показатели 3-го года:
![]() тыс. ед.
тыс. ед.
![]()
![]() тыс. ед. на 1%
тыс. ед. на 1%
Контроль: ![]()
4) Найдём темп роста ![]() и 4-й уровень ряда из формулы
и 4-й уровень ряда из формулы ![]() :
:
![]() тыс. шт.
тыс. шт.
Оставшиеся показатели:
![]() тыс. шт.
тыс. шт.
![]() тыс. ед. на 1%
тыс. ед. на 1%
Контроль: ![]()
5) Пятый уровень ряда найдём из соотношения: ![]() тыс. ед., после чего рассчитаем остальные показатели года:
тыс. ед., после чего рассчитаем остальные показатели года:
![]() тыс. ед.
тыс. ед.
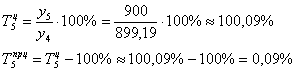
![]() тыс. ед. на 1% (Примечание: использовали точное значение
тыс. ед. на 1% (Примечание: использовали точное значение ![]() ).
).
Контроль: ![]()
6) Ну и тут по аналогии со 2-м годом:
![]() тыс. ед.
тыс. ед.
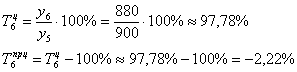
![]() тыс. ед. на 1%, что и требовалось проверить.
тыс. ед. на 1%, что и требовалось проверить.
Результаты сведём в таблицу:
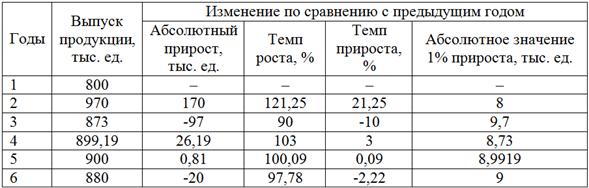
Определим средний за 6 лет выпуск продукции:
![]() тыс. ед.
тыс. ед.
Средний абсолютный прирост:
![]() тыс. ед.
тыс. ед.
Средний темп роста:
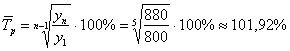
и темп прироста:
![]()
Краткие выводы: максимальное увеличение выпуска продукции наблюдалось во 2-й год: +170 тыс. ед., что составило +21,25% по отношению к 1-му году. После чего произошёл спад (-10%) и стагнация показателя. За 6 лет выпуск продукции увеличивался на 16 тыс. ед. и +1,92% в среднем за год.
Примечание: если в задаче рассматриваются только базисные или только цепные показатели, то обозначения можно упростить, не снабжая их уточняющими индексами:
![]()
О каких показателях идёт речь (базисных или цепных) будет понятно из контекста.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright