


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Сглаживание временнОго ряда
Продолжаем изучать динамические ряды. Или, что то же самое, ряды динамики, временнЫе ряды, хронологические ряды. На всякий случай вспомним, что это такое :) Это упорядоченная по времени последовательность значений некоторого показателя, например:

В первой строке указаны временнЫе промежутки, обычно они имеют равную длину, во второй – уровни ряда, в нашем примере – количество произведённой продукции в некоторых единицах. Представьте, что это молоко, самое страшное, с чем вас могут «застукать». Или фисташки. Чтобы было интереснее решать задачу :) …Да, и запОмните термин, кто ещё не успел запомнить, уровни – это циферки во второй строке.
На предыдущем уроке мы рассмотрели показатели интенсивности изменения уровней ряда, базисные, цепные, средние. Говоря простым языком, это то – насколько резво меняются значения. Так, во 2-м году производство молока выросло на ![]() единицы по отношению к 1-му году (абсолютный прирост) или в
единицы по отношению к 1-му году (абсолютный прирост) или в ![]() раз (коэффициент роста). …Хватит улыбаться. В процентах увеличение составило
раз (коэффициент роста). …Хватит улыбаться. В процентах увеличение составило ![]() (темп прироста).
(темп прироста).
Но, помимо сих и иже с ними показателей, к уровням ряда можно подойти с другой стороны. А именно, проанализировать тенденцию – вот производство продукции, оно преимущественно растёт с течением времени или уменьшается? Или остаётся примерно одним и тем же?
Другая компонента – это возможная цикличность уровней. Так, если мы исследуем продажу мороженого по месяцам, то совершенно ясно, что к летнему сезону они будут возрастать, а осенью падать. И это, очевидно, повторяется циклами, из года в год. Другой яркий пример – количество вызов такси в зависимости от времени суток. Цикличности, разумеется, может и не быть – так, скорее всего, обстоят дела в нашем примере с годовыми интервалами. …Ну если только циклично меняется мода на молоко из поклонения в поколение :)
И, наконец, в жизни есть место случайности. Уровни ряда заранее не определены, и всегда могли оказаться как побольше, так и поменьше фактически зафиксированных значений. Это обусловлено воздействием случайных факторов, заранее непредсказуемых и непрогнозируемых.
К слову о птичках. Ряд динамики лишь формально отражает изменение уровней с течением времени, но ничего нам не говорит о ФАКТОРАХ, влияющих на это изменение. И в самом деле, глядя на числа в таблице, мы не можем сказать, что именно явилось причиной именно такой динамики производства. Однако, даже за неимением информации, все факторы можно разделить на три большие группы, что мы уже сделали только что. Есть факторы, которые формируют тенденцию, цикличность и случайные колебания уровней ряда.
На практике, прежде всего, обычно исследуют тенденцию, и давайте сразу зарядим задачу:
Пример 1
Имеются следующие данные о деятельности предприятия:

Требуется исследовать тенденцию ряда:
1) методом укрупнения интервалов;
2) графическим способом;
3) методом скользящей трёхзвенной средней;
4) методом аналитического выравнивания по прямой.
По результатам пунктов 2-4 выполнить общий чертёж и спрогнозировать производство продукции в 11-м году. Ну, и конечно, сделать выводы по каждому пункту.
Решение: 1) Окидывая взглядом числа, сразу трудно сделать вывод о преимущественной тенденции: мы видим как убывание, так и возрастание значений. И самый быстрый способ анализа – это укрупнить интервалы, при этом желательно задействовать все уровни. Ещё с советских времён у нас на слуху пятилетний план.
Вычислим суммарное производство за 1-ю пятилетку, не откажу себе в удовольствии пощёлкать по кнопкам своего старого калькулятора:
![]() ед.
ед.
и за 2-ю пятилетку:
![]() ед.
ед.
Кратко и сурово: производство увеличилось.
2) Другой, простой и эффективный способ исследования – это построить график и посмотреть, что происходит. …Прямо как в той истории из истории: чтобы сбить самолёт-«невидимку» (stealth) , нужно посмотреть в небо и его сбить :)
По оси абсцисс откладываем годы, по оси ординат – уровни ряда:
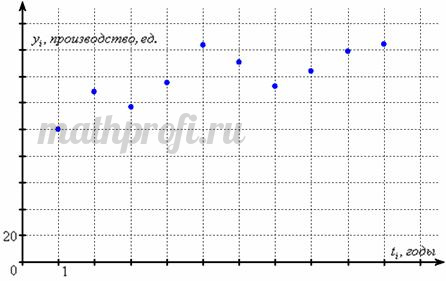
И, в общем-то всё понятно: производство, пусть со спадами, но преимущественно растёт.
3) Метод скользящей средней состоит в расчёте средних значений нескольких соседних уровней (звеньев), на практике популярно брать по три штуки.
Вычислим среднее арифметическое первых трёх уровней:
![]() ед.,
ед.,
среднее арифметическое 2-го, 3-го и 4-го уровней:
![]() ед.,
ед.,
3-го, 4-го и 5-го уровней:
![]() ед.,
ед.,
… и так далее,
и наконец, 8-го, 9-го и 10-го уровней:
![]() ед.
ед.
Вычисления удобно проводить в Экселе, а результаты оформлять таблицей:

Изобразим на том же чертеже найденные средние значения и соединим их ломаной (зелёный цвет):
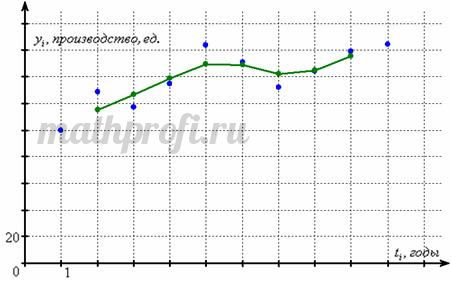
Это и есть сглаживание ряда динамики скользящей трёхзвенной средней. Скользящая средняя сглаживает колебания уровней и позволяет более чётко увидеть тенденцию.
Существуют и другие разновидности скользящих средних, с разным количеством звеньев, разными подходами к вычислению средних значений, соединённые гладкими линиями, и так далее, вариаций масса.
4) Проведём аналитическое выравнивание по прямой. С этим заданием мы уже сталкивались в других темах, и, переводя на обывательский язык, вновь поясню суть: нам нужно подобрать такую прямую, которая проходила бы как можно ближе к большинству точек. Обычно используют метод наименьших квадратов, и решение идёт по шаблону.
Заполним расчётную таблицу, в правом столбце подобьём суммы:

О том, как это быстро подсчитать в Экселе, есть видео (копия тут), впрочем, может быть, ещё запилю отдельный ролик.
Коэффициенты «а» и «бэ» искомого уравения ![]() найдём как решение системы:
найдём как решение системы:
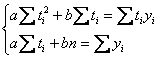 , где
, где ![]() – количество уровней, ну и нужные суммы рассчитаны:
– количество уровней, ну и нужные суммы рассчитаны:
![]()
Систему решим по формулам Крамера, и это самая настоящая нетленка. Вычислим главный определитель системы:
![]() , значит, система имеет единственное решение.
, значит, система имеет единственное решение.

Таким образом, искомое уравнение регрессии:
![]()
Уравнение показывает, что каждый год производство продукции в среднем увеличивалось примерно на 5,485 единиц.
Найдём две точки для построения прямой:
![]() ед.,
ед.,
![]() ед. – вот заодно и прогноз на 11-й год получился, и добавим, как модно говорить, линию тренда на чертёж:
ед. – вот заодно и прогноз на 11-й год получился, и добавим, как модно говорить, линию тренда на чертёж:
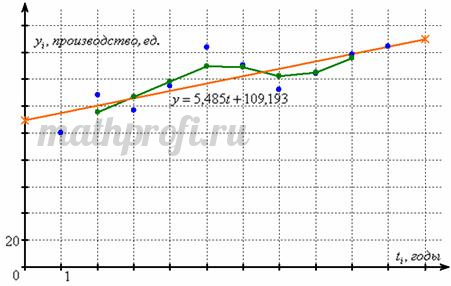
Формально, функция ![]() – есть зависимость производства от времени, однако опять же подчеркнём, что на количество произведённой продукцию, разумеется, влияют другие факторы, «оставшиеся за кадром».
– есть зависимость производства от времени, однако опять же подчеркнём, что на количество произведённой продукцию, разумеется, влияют другие факторы, «оставшиеся за кадром».
При желании или по необходимости можно найти линейный коэффициент корреляции и оценить статистическую значимость модели. Говоря проще выяснить, лажа получилась в 4-м пункте или нет. Впрочем, давайте выясним, даже интересно стало. Вычислим средние значения:
![]()
и стандартные отклонения:
![]()
промежуточные вычисления, их можно оформить 5-й строкой в таблице выше:
![]()
и:
![]()
В результате:
![]() – коэффициент корреляции положителен, достаточно близок к единице, таким образом, существует сильная прямая зависимость количества произведённой продукции от времени (хотя фактически, конечно, не от него).
– коэффициент корреляции положителен, достаточно близок к единице, таким образом, существует сильная прямая зависимость количества произведённой продукции от времени (хотя фактически, конечно, не от него).
Проверим статическую значимость коэффициента. Для этого рассмотрим нулевую гипотезу о том, что коэффициент корреляции на самом деле равен нулю ![]() (то есть полученный результат
(то есть полученный результат ![]() статистически случаен) – против альтернативной гипотезы
статистически случаен) – против альтернативной гипотезы ![]() на уровне значимости
на уровне значимости ![]() . Для проверки гипотезы используем статистический критерий
. Для проверки гипотезы используем статистический критерий ![]() .
.
Для уровня значимости ![]() и количества степеней свободы
и количества степеней свободы ![]() найдём критическое значение двусторонней критической области:
найдём критическое значение двусторонней критической области:
![]() – это значение можно определить по таблице критических точек распределения Стьюдента (ориентируемся по верхней строке) либо с помощью соответствующей функции Экселя (пункт 10в).
– это значение можно определить по таблице критических точек распределения Стьюдента (ориентируемся по верхней строке) либо с помощью соответствующей функции Экселя (пункт 10в).
…«Накладка» тут получилась с буквой «тэ малое», к временнОму ряду, она, естественно, отношения не имеет. Ну да ладно, мелочи жизни.
Вычислим наблюдаемое значение критерия:
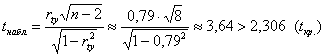 , таким образом, на уровне значимости
, таким образом, на уровне значимости ![]() гипотезу
гипотезу ![]() отвергаем в пользу гипотезы
отвергаем в пользу гипотезы ![]() .
.
Иными словами, значение ![]() статистически значимо и вряд ли объяснимо случайными факторами (малым количество наблюдений, например).
статистически значимо и вряд ли объяснимо случайными факторами (малым количество наблюдений, например).
Из статистической значимости коэффициента корреляции автоматически следует значимость коэффициента ![]() и статистическая значимость всего уравнения регрессии
и статистическая значимость всего уравнения регрессии ![]() . То есть, с точки зрения математической статистики, тенденция (рост) почти наверняка есть, и полученное уравнение хорошо характеризует динамику, в частности пригодно для прогнозирования, чем мы уже воспользовались ранее.
. То есть, с точки зрения математической статистики, тенденция (рост) почти наверняка есть, и полученное уравнение хорошо характеризует динамику, в частности пригодно для прогнозирования, чем мы уже воспользовались ранее.
Следует добавить, что линейная модель – далеко не единственная, существуют и нелинейные, в чём мы опять же уже потренировались. Всё зависит от условия той или иной задачи.
Но довольно лирики, следующая задача – самостоятельно:
Пример 2
Имеются данные о товарообороте маркетплейса за 12 месяцев отчетного года:

…Экономисты тут поинтересуются, сопоставимы ли цены, но задание техническое, инфляцией пренебрежем. Да и числа я тоже сильно округлил везде, чтобы от таблиц не рябило в глазах, сейчас важно отработать само решение.
Требуется проанализировать тенденцию динамического ряда:
1) методом укрупнения интервалов, 2) графически, 3) методом трёхзвенной скользящей средней, 4) методом аналитического выравнивания по прямой.
По результатам пунктов 2-4 выполнить чертёж.
Факультативно, а даже и не факультативно: 5) найдите коэффициент линейной детерминации и проверьте статистическую значимость уравнения регрессии на уровне значимости ![]() .
.
Ну и, конечно, сделать краткие выводы – эй, ребята, изучающие датасайенс, так что же там происходит с маркетплейсом? И предугадывая леность студента, все числа, как повелось, уже забиты в Эксель :)
Решаем, думаем, сверяемся, и тема временнЫх рядов далеко не закончена… Только аппетит появился, даже можно сказать :)
Пример 2. Решение: 1) Проведём анализ тенденции методом укрупнения интервалов, напрашивается поквартально:
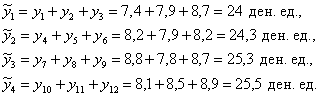
И очевидно, что товарооборот во 2-м полугодии несколько увеличился.
2) Изобразим уровни ряда на чертеже (синие точки на рисунке ниже). Из анализа их расположения трудно сделать вывод о какой-либо тенденции, скорее, они колеблются около некоторого постоянного значения.
3) Выполним сглаживание ряда трёхзвенной скользящей средней. Для этого рассчитаем средние значения по тройкам смежным интервалам:

– добавим на чертёж соответствующие точки и соединим их ломаной линией (зелёный цвет). И из внешнего вида ломаной опять же затруднительно сделать вывод о тенденции; можно предположить некоторый рост, но выглядит он неубедительно.
4) Выполним аналитическое выравнивание по прямой, используем метод наименьших квадратов. Заполним расчётную таблицу, в правом столбце подсчитаем суммы:

Коэффициенты уравения ![]() найдём как решение системы:
найдём как решение системы:
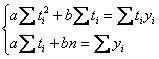 , где
, где ![]() , в данном случае:
, в данном случае:
![]()
Систему решим методом Крамера:
![]() , значит, система имеет единственное решение.
, значит, система имеет единственное решение.

Таким образом, искомое уравнение:
![]()
Найдём две точки для построения прямой:
![]()
и добавим её на чертёж:
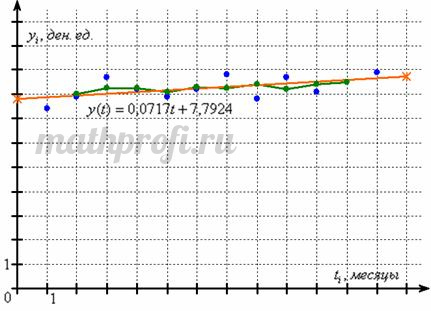
Уравнение показывает, что каждый месяц товарооборот в среднем увеличивается примерно на 0,0717 ден. ед. Соответствующая прямая показывает небольшой рост, но можно ли доверять полученным результатам с точки зрения статистики?
5) Проверим статистическую значимость модели. Найдём коэффициент детерминации. Для этого вычислим средние значения:
![]() ,
,
и стандартные отклонения:
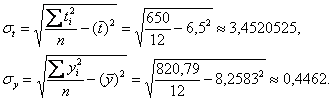
Таким образом, коэффициент корреляции:
![]()
и коэффициент детерминации:
![]() , то есть в рамках построенной модели только 30,75% вариации товарооборота объяснимо временнЫм фактором (точнее, фактором стоЯщим за ним).
, то есть в рамках построенной модели только 30,75% вариации товарооборота объяснимо временнЫм фактором (точнее, фактором стоЯщим за ним).
5) Проверим статистическую значимость коэффициента детерминации, а значит, уравнения ![]() и суть – всей модели. А именно, гипотезу о том, что на самом деле
и суть – всей модели. А именно, гипотезу о том, что на самом деле ![]() (то есть значение
(то есть значение ![]() статистически случайно) против гипотезы
статистически случайно) против гипотезы ![]() на уровне значимости
на уровне значимости ![]() . Используем критерий
. Используем критерий ![]() Фишера.
Фишера.
Для заданного уровня значимости и количества степеней свободы ![]() с помощью соответствующей функции Экселя (пункт 12) определим критическое значение критерия:
с помощью соответствующей функции Экселя (пункт 12) определим критическое значение критерия:
![]()
Вычислим наблюдаемое значение критерия:
![]() , поэтому на уровне значимости
, поэтому на уровне значимости ![]() нет оснований отвергать гипотезу
нет оснований отвергать гипотезу ![]() .
.
Таким образом, с точки зрения статистики, построенная модель является «плохой» и её крайне нежелательно использовать, в частности для прогнозирования. Но самое главное, нет оснований утверждать, что тенденция вообще существует; несмотря на то, что мы видим небольшой рост товарооборота, нельзя утверждать, что он обусловлен системными (постоянно действующими) факторами. Возможно, причина тому сезонность или, например, разовое увеличение рынка сбыта.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright