Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Замечательные пределы.
Примеры решений

Продолжаем наш разговор на тему Пределы и способы их решения, и перед тем как продолжить, настоятельно рекомендую ознакомиться с указанной статьей. Там я объяснил, ЧТО такое предел, и это ОЧЕНЬ важно. Можно не понимать, что такое определитель и успешно их решать, можно совершенно не понимать, что такое производная и находить их на «пятёрку». Но вот если Вы не понимаете, что такое предел, то с практикой придётся туго. Также не лишним будет ознакомиться с образцами оформления решений и моими рекомендациями по оформлению. Вся информация изложена в простой и доступной форме.

А для целей данного урока нам потребуются следующие справочные материалы: Замечательные пределы и Тригонометрические формулы (откроются по соседству). Файлы сохраните и по возможности распечатайте – это значительно удобнее, к тому же к сим справкам часто придётся обращаться в оффлайне.

Чем же замечательны замечательные пределы? Замечательность данных пределов состоит в том, что они доказаны математиками прошлого, и благодарным потомкам не приходится мучаться страшными пределами с нагромождением тригонометрических функций, логарифмов, степеней. То есть при нахождении пределов мы будем пользоваться готовыми результатами, установленными теоретически.

Замечательных пределов существует несколько, но на практике у студентов в 95% случаев фигурируют два замечательных предела: Первый замечательный предел и Второй замечательный предел. Следует отметить, что это исторически сложившиеся названия, и, когда, например, говорят о «первом замечательном пределе», то подразумевают под этим вполне определённую вещь, а не какой-то случайный, взятый с потолка предел.

Начнём.

Первый замечательный предел

Рассмотрим следующий предел: .

Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределённостью вида , которую, к счастью, раскрывать не нужно. В курсе математического анализа доказано, что:

Это и есть Первый замечательный предел. Но самое вкусное, что внутри предела ВМЕСТО «икс» может располагаться функция «альфа от икс», и если она стремится к нулю  при , то получаем тот же самый замечательный результат:

Нередко в практических заданиях встречается «перевёртыш», это ничего не меняет:

, в частности: .

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде , то и решать его нужно в таком же виде, ничего не переставляя.

Далее для простоты первым замечательным пределом будем называть все перечисленные варианты.

Примеры:
, , ,

Здесь , , , , и всё гуд – первый замечательный предел применИм.

А вот следующая запись – ересь:

Почему? Потому что многочлен  не стремится к нулю, он стремится к пятерке.

Кстати, вопрос на засыпку, а чему равен предел ? Ответ в конце урока.

А теперь, уважаемый студент, запомни «намертво»:  – это может оказать неоценимую помощь на зачёте / экзамене, когда вопрос будет решаться между «двойкой» и «тройкой», и преподаватель поинтересуется, «А может он (а) все-таки чего знает?!».

Базовые элементарные факты нужно знать. Иначе высок риск даже не «неуд» получить, а стать перспективным кандидатом на «вылет».

Переходим к рассмотрению практических примеров:

Пример 1

Найти предел

Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.

Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):

Итак, у нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .

В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».

А делается это очень просто:

То есть знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.

Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:

Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:

Теперь только осталось избавиться от трехэтажности дроби:

Кто позабыл упрощение многоэтажных дробей, пожалуйста, освежите материал в справочнике Горячие формулы школьного курса математики.

Готово. Окончательный ответ: , его лучше оставить в таком виде.

Если не хочется использовать пометки карандашом, то решение можно оформить так:

“

Используем первый замечательный предел (формулу можно не указывать, её все знают)

“

Пример 2

Найти предел

Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:

Действительно, у нас неопределенность  , поэтому попытаемся организовать первый замечательный предел. На уроке Пределы. Примеры решений мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени представим в виде произведений:

Далее, по уже знакомой схеме, организовываем первые замечательные пределы. Под синусами у нас , значит, в числителе тоже нужно получить :

Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:

Собственно, ответ готов:

В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.

Пример 3

Найти предел

Подставляем ноль в выражение под знаком предела:

Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле  

(к слову, с котангенсом поступают аналогично, см. Тригонометрические формулы).

 В данном случае:

Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):

Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.

Дальше по накатанной схеме, организуем первый замечательный предел:

Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:

В итоге получена бесконечность, бывает и такое.

Пример 4

Найти предел

Пробуем подставить ноль в числитель и знаменатель:

Получена неопределенность  (косинус нуля, как мы помним, равен единице)

Используем тригонометрическую формулу . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.

Постоянные множители вынесем за значок предела:

Организуем первый замечательный предел:

Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:

Избавимся от трехэтажности:

Предел фактически решен, указываем, что оставшийся синус стремится к нулю:

Пример 5

Найти предел

Этот пример сложнее, попробуйте разобраться самостоятельно:

Готово. Ответ, напоминаю, лучше оставить в виде неправильной дроби.

Некоторые пределы можно свести к 1-му замечательному пределу путём замены переменной, но об этом позже.

Второй замечательный предел

В теории математического анализа доказано, что:

Исторически эта формула появилась в результате решения конкретной задачи – о начислении сложных процентов, её и назвали Вторым замечательным пределом.

Справка:  – это иррациональное число.

И аналогично, внутри ВМЕСТО  может располагаться функция , и если  либо при , то:

Факультативно сообщаю, что «икс» может стремиться и к «минус» бесконечности, и если при этом либо , то:
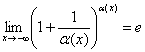, в частности , но эти случаи редкость.

Далее для удобства все перечисленные варианты (и даже больше) будем называть вторым замечательным пределом.

Пример 6

Найти предел

Наверняка Вы обратили внимание, что в пределах бесконечность без знака означает «плюс» бесконечность. Это, конечно, небрежность, но так повелось. И после сего примечания для неопытных практиков и въедливых теоретиков переходим к решению.

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое значение «икс» в выражение  , по какому принципу это делается, разобрано на уроке Пределы. Примеры решений.

Нетрудно заметить, что при  основание степени , а показатель – , то есть имеется неопределенность вида :

Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как оно обычно бывает, замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно организовать искусственно. Рассуждать можно следующим образом: в данном примере (стремится к + бесконечности), значит, в показателе нам тоже нужно организовать  . Для этого возводим основание в степень , и, чтобы выражение не изменилось – возводим в степень :

Когда задание оформляется от руки, карандашом помечаем:

Практически всё готово, страшная степень превратилась в симпатичную букву :

При этом сам значок предела перемещаем в показатель:

Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.

Пример 7

Найти предел

Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.

Пробуем подставить бесконечно большое значение «икс» в функцию:

В результате получена неопределенность . Но второй замечательный предел применИм к неопределенности вида . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас , значит, в числителе тоже нужно организовать :

Теперь можно почленно разделить числитель на знаменатель:

Вроде бы основание стало напоминать , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:

Таким образом, основание приняло вид , и, более того, появилась нужная нам неопределенность . Организуем второй замечательный предел.
Легко заметить, что в данном примере . Заметьте, что эта функция стремится к «минус» бесконечности, но это не меняет дела. Снова исполняем наш искусственный прием: возводим основание степени в , и, чтобы выражение не изменилось – возводим в обратную дробь :

Наконец-то долгожданное  устроено, с чистой совестью превращаем его в букву :

Но на этом квест не закончен, в показателе у нас появилась неопределенность вида , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на :

Готово. …Не очень тут разборчиво местами получается, но увеличение картинок не помогло, ещё хреновее даже выглядит.

На практике время от времени можно встретить модификацию второго замечательного предела – его «перевёртыш», который в общем виде записывается так:

, если , в частности: .

Пример 8

Найти предел

Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое значение) в функцию:

В результате получена знакомая неопределенность . Очевидно, что в данном примере , и эта функция стремится к нулю. С помощью знакомого искусственного приема организуем в показателе степени конструкцию :

Выражение  со спокойной душой превращаем в букву :

Ещё не всё, в показателе у нас появилась неопределенность вида . Раскладываем тангенс на синус и косинус (ничего не напоминает?):

Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении:

А что такое  и к чему оно стремится, нужно уже знать, иначе «двойка»!

Как видите, в практических заданиях на вычисление пределов нередко требуется применить сразу несколько правил и приемов.

Повторюсь, что на практике Вам с высочайшей вероятностью встретятся именно первый и второй замечательные пределы. Как быть, если попался «экзотический» экземпляр? Спокойно, решаем по аналогии с 1-м замечательным пределом + дополнительные фишки, с некоторыми примерами можно ознакомиться во 2-м параграфе статьи Сложные пределы.

...Да, так чему же равен предел ?

Если у Вас получился ответ , значит, с пониманием темы не всё так безнадежно = )

Далее по курсу Методы решения пределов, где мы продолжим разбираться в пределах функций и закрепим материал.

Желаю успехов!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте