


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Бесконечно малые функции.
Замечательные эквивалентности в пределах
Продолжаем учебный цикл «пределы для чайников», который открылся статьями Пределы. Примеры решений и Замечательные пределы. Если вы впервые на сайте, рекомендую также ознакомиться с уроком Методы решения пределов, который значительно улучшит вашу студенческую карму. В третьем мануале мы рассмотрели бесконечно большие функции, их сравнение, и сейчас настало время вооружиться лупой, чтобы после Страны великанов заглянуть в Страну лилипутов. Я провёл новогодние каникулы в культурной столице и вернулся в очень хорошем настроении, поэтому чтение обещает быть особо интересным.
В данной статье будут подробно разобраны бесконечно малые функции, с которыми вы на самом деле уже неоднократно сталкивались, и их сравнение. С невидимыми событиями вблизи нуля тесно связаны многие замечательные пределы, замечательные эквивалентности, и практическая часть урока, в основном, посвящена как раз вычислению пределов с использованием замечательных эквивалентностей.
Бесконечно малые функции. Сравнение бесконечно малых
Что тут сказать… Если существует предел ![]() , то функция
, то функция ![]() называется бесконечно малой в точке
называется бесконечно малой в точке ![]() .
.
Существенным моментом утверждения является тот факт, что функция может быть бесконечно малой лишь в конкретной точке.
Начертим знакомую линию ![]() :
:
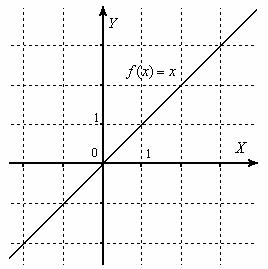
Данная функция бесконечно малА в единственной точке: ![]()
Следует отметить что, в точках «плюс» бесконечность и «минус» бесконечность эта же функция будет уже бесконечно большой: ![]() . Или в более компактной записи:
. Или в более компактной записи: ![]()
Во всех других точках, предел функции будет равен конечному числу, отличному от нуля.
Таким образом, не существует такого понятия как «просто бесконечно малая функция» или «просто бесконечно большая функция». Функция может быть бесконечно малой или бесконечно большой только в конкретной точке.
! Примечание: для краткости я часто буду говорить «бесконечно малая функция», подразумевая, что она бесконечно малА в рассматриваемой точке.
Таких точек может быть несколько и даже бесконечно много. Изобразим какую-нибудь непуганую параболу:
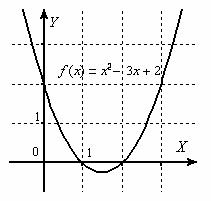
Представленная квадратичная функция является бесконечно малой в двух точках – в «единице» и в «двойке»: ![]()
Как и в предыдущем примере, на бесконечности данная функция является бесконечно большой: ![]()
Смысл двойных знаков:
Запись ![]() обозначает, что при
обозначает, что при ![]() , а при
, а при ![]() .
.
Запись ![]() обозначает, что при
обозначает, что при ![]() , а при
, а при ![]() .
.
Запись ![]() обозначает, что и при
обозначает, что и при ![]() , и при
, и при ![]() .
.
Запись ![]() обозначает, что и при
обозначает, что и при ![]() , и при
, и при ![]() .
.
Прокомментированный принцип «расшифровки» двойных знаков справедлив не только для бесконечностей, но и для любых конечных точек, функций и ряда других математических объектов.
А теперь синус ![]() . Это пример, когда функция бесконечно малА в бесконечном количестве точек:
. Это пример, когда функция бесконечно малА в бесконечном количестве точек:
![]()
Действительно, синусоида «прошивает» ось абсцисс через каждое «пи»:
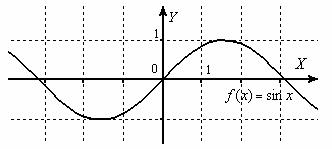
Заметьте, что сверху/снизу функция ограничена, и не существует такой точки, в которой бы она была бесконечно большой, синусу остаётся разве что облизываться на бесконечность.
Отвечу ещё на пару простых вопросов:
Может ли функция быть бесконечно малой на бесконечности?
Конечно. Таких экземпляров воз и маленькая тележка.
Элементарный пример: ![]() . Геометрический смысл данного предела, к слову, проиллюстрирован в статье Графики и свойства функций.
. Геометрический смысл данного предела, к слову, проиллюстрирован в статье Графики и свойства функций.
Может ли функция НЕ БЫТЬ бесконечно малой?
(в любой точке области определения)
Да. Очевидный пример – квадратичная функция, график которой (парабола) не пересекает ось ![]() . Обратное утверждение, кстати, в общем случае неверно – гипербола из предыдущего вопроса, хоть и не пересекает ось абсцисс, но бесконечно малА на бесконечности.
. Обратное утверждение, кстати, в общем случае неверно – гипербола из предыдущего вопроса, хоть и не пересекает ось абсцисс, но бесконечно малА на бесконечности.
Сравнение бесконечно малых функций
В статье Методы решения пределов были подробно рассмотрены гиганты, которые мерялись между собой порядком роста, и ситуацию контролировала самая большая особь. Общество карликов устроено точно так же, только соревнуются они в другой весовой категории – порядке малости. Среди лилипутов тоже существуют свои великаны, кто самый крупный – тот и девушку танцует. Проясним ситуацию. Рассмотрим следующую бесконечно малую функцию:
![]()
Да, совершенно понятно, что предел равен нулю, но обратим внимание на довольно любопытную вещь: в пределе находится сумма функций ![]() , и некоторые из них будут стремиться к нулю быстрее, а некоторые – медленнее. Об этом я уже немного рассказывал в Примере № 7 урока Методы решения пределов.
, и некоторые из них будут стремиться к нулю быстрее, а некоторые – медленнее. Об этом я уже немного рассказывал в Примере № 7 урока Методы решения пределов.
Построим последовательность ![]() , которая стремится к нулю, и вычислим несколько значений трёхчлена
, которая стремится к нулю, и вычислим несколько значений трёхчлена ![]() :
:

Очевидно, что с уменьшением значений «икс», функция ![]() убегает к нулю быстрее всех остальных (её значения обведены красным цветом). Говорят, что функция
убегает к нулю быстрее всех остальных (её значения обведены красным цветом). Говорят, что функция ![]() более высокого порядка малости, чем функции
более высокого порядка малости, чем функции ![]() , а также более высокого порядка малости, чем
, а также более высокого порядка малости, чем ![]() . Но быстро бегать в Стране лилипутов – не есть доблесть, «тон задаёт» самый нерасторопный карлик
. Но быстро бегать в Стране лилипутов – не есть доблесть, «тон задаёт» самый нерасторопный карлик ![]() , который, как и полагается боссу, идёт к нулю медленнее всех. Именно от него зависит, насколько быстро сумма
, который, как и полагается боссу, идёт к нулю медленнее всех. Именно от него зависит, насколько быстро сумма ![]() приблизится к нулю:
приблизится к нулю:

Образно говоря, бесконечно малая функция ![]() «поглощает» всё остальное, что особенно хорошо видно по итоговому результату третьей строки. Иногда говорят, что
«поглощает» всё остальное, что особенно хорошо видно по итоговому результату третьей строки. Иногда говорят, что ![]() более низкого порядка малости, чем
более низкого порядка малости, чем ![]() и их сумма.
и их сумма.
В рассмотренном пределе, всё это, конечно, не имеет особого значения, ведь в результате всё равно получается ноль. Однако «лилипуты-тяжеловесы» начинают играть принципиально важную роль в пределах с дробями. Начнём с примеров, которые, пусть редко, но встречаются в реальных практических работах:
Пример 1
Вычислить предел
![]()
Здесь неопределённость ![]() , и из вводного урока о пределах функций вспоминаем общий принцип раскрытия данной неопределённости: нужно разложить числитель и знаменатель на множители, а потом что-нибудь сократить:
, и из вводного урока о пределах функций вспоминаем общий принцип раскрытия данной неопределённости: нужно разложить числитель и знаменатель на множители, а потом что-нибудь сократить:
![]()
На первом шаге в числителе выносим за скобки ![]() , а в знаменателе «икс». На втором шаге сокращаем числитель и знаменатель на «икс», устраняя тем самым неопределённость. Указываем, что оставшиеся «иксы» стремятся к нулю, и получаем ответ.
, а в знаменателе «икс». На втором шаге сокращаем числитель и знаменатель на «икс», устраняя тем самым неопределённость. Указываем, что оставшиеся «иксы» стремятся к нулю, и получаем ответ.
В пределе получилась баранка, следовательно, функция числителя более высокого порядка малости, чем функция знаменателя. Или короче: числитель более высокого порядка малости, чем знаменатель. Что это значит? Числитель стремится к нулю быстрее, чем знаменатель, именно поэтому в итоге и получился ноль.
Как и в случае с бесконечно большими функциями, ответ можно узнать заранее. Приём аналогичен, но отличается тем, что в числителе и в знаменателе нужно МЫСЛЕННО отбросить все слагаемые со СТАРШИМИ степенями, поскольку, как отмечалось выше, определяющее значение имеют медленные карлики:
![]()
Пример 2
Вычислить предел
![]()
Ноль на ноль…. Давайте сразу узнаем ответ: МЫСЛЕННО отбросим все старшие слагаемые (быстрых карликов) числителя и знаменателя:
![]()
Алгоритм решения, точно такой же, как и в предыдущем примере:
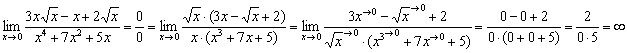
В данном примере знаменатель более высокого порядка малости, чем числитель. При уменьшении значений «икс», самый медленный карлик числителя (и всего предела) ![]() становится настоящим монстром по отношению к своему более быстрому оппоненту
становится настоящим монстром по отношению к своему более быстрому оппоненту ![]() . Например, если
. Например, если ![]() , то
, то ![]() – уже в 40 раз больше…. не монстр ещё, конечно, при данном значении «икс», но такой уже субъект с большим пивным животом.
– уже в 40 раз больше…. не монстр ещё, конечно, при данном значении «икс», но такой уже субъект с большим пивным животом.
И совсем простой демонстрационный предел:
Пример 3
Вычислить предел
![]()
Узнаем ответ, МЫСЛЕННО отбросив все старшие слагаемые числителя и знаменателя:
![]()
Решаем:
![]()
В результате получено конечное число. Хозяин числителя ровно в два раза толще начальника знаменателя. Это ситуация, когда числитель и знаменатель одного порядка малости.
На самом деле сравнение бесконечно малых функций давно фигурировало на предыдущих уроках:
![]() (Пример № 4 урока Пределы. Примеры решений);
(Пример № 4 урока Пределы. Примеры решений);
![]() (Пример № 17 урока Методы решения пределов) и т. д.
(Пример № 17 урока Методы решения пределов) и т. д.
Напоминаю заодно, что «икс» может стремиться не только к нулю, но и к произвольному числу, а также к бесконечности.
Что принципиально важно во всех рассмотренных примерах?
Во-первых, предел должен вообще существовать в данной точке. Например, предела 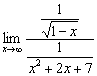 не существует. Если
не существует. Если ![]() , то функция числителя
, то функция числителя ![]() не определена в точке «плюс» бесконечность (под корнем получается бесконечно большое отрицательное значение). Подобные, казалось бы, вычурные примеры встречаются на практике:
не определена в точке «плюс» бесконечность (под корнем получается бесконечно большое отрицательное значение). Подобные, казалось бы, вычурные примеры встречаются на практике: 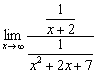 , как ни неожиданно, здесь тоже сравнение бесконечно малых функций и неопределённость «ноль на ноль». Действительно, если
, как ни неожиданно, здесь тоже сравнение бесконечно малых функций и неопределённость «ноль на ноль». Действительно, если ![]() , то
, то ![]() . …Решение? Избавляемся от четырёхэтажности дроби, получаем неопределённость
. …Решение? Избавляемся от четырёхэтажности дроби, получаем неопределённость ![]() и раскрываем её стандартным методом.
и раскрываем её стандартным методом.
Возможно, начинающих изучать пределы сверлит вопрос: «Как так? Вот есть неопределённость 0:0, но на ноль же делить нельзя!». Совершенно верно, нельзя. Рассмотрим тот же предел ![]() . Функция
. Функция ![]() не определена в точке «ноль». Но этого, вообще говоря, и не требуется, важно чтобы функция существовала В ЛЮБОЙ бесконечно близкой к нулю точке (или более строго – в любой бесконечно малой окрестности нуля). То есть
не определена в точке «ноль». Но этого, вообще говоря, и не требуется, важно чтобы функция существовала В ЛЮБОЙ бесконечно близкой к нулю точке (или более строго – в любой бесконечно малой окрестности нуля). То есть ![]() – это символическое обозначение, здесь подразумеваются не нули, а бесконечно малые значения.
– это символическое обозначение, здесь подразумеваются не нули, а бесконечно малые значения.
ВАЖНЕЙШАЯ ОСОБЕННОСТЬ ПРЕДЕЛА, КАК ПОНЯТИЯ
состоит в том, что «икс» бесконечно близко приближается к некоторому значению ![]() , однако его – он не достигает! Но стремится =) Таким образом, для существования предела функции в точке
, однако его – он не достигает! Но стремится =) Таким образом, для существования предела функции в точке ![]() не имеет значения, определена ли там сама функция или нет. Более подробно об этом можно прочитать в статье Пределы по Коши, ну а пока что вернёмся к теме сегодняшнего урока:
не имеет значения, определена ли там сама функция или нет. Более подробно об этом можно прочитать в статье Пределы по Коши, ну а пока что вернёмся к теме сегодняшнего урока:
Во-вторых, функции числителя и знаменателя должны быть бесконечно малЫ в данной точке. Так, например, предел ![]() совсем из другой команды, здесь функция числителя не стремится к нулю:
совсем из другой команды, здесь функция числителя не стремится к нулю: ![]() .
.
Систематизируем информацию о сравнении бесконечно малых функций:
Пусть ![]() – бесконечно малые функции в точке
– бесконечно малые функции в точке ![]() (т. е.
(т. е. ![]() при
при ![]() ) и существует предел их отношений
) и существует предел их отношений ![]() . Тогда:
. Тогда:
1) Если ![]() , то функция
, то функция ![]() более высокого порядка малости, чем
более высокого порядка малости, чем ![]() .
.
Простейший пример: ![]() , то есть кубическая функция более высокого порядка малости, чем квадратичная.
, то есть кубическая функция более высокого порядка малости, чем квадратичная.
2) Если ![]() , то функция
, то функция ![]() более высокого порядка малости, чем
более высокого порядка малости, чем ![]() .
.
Простейший пример: ![]() , то есть кубическая функция более высокого порядка малости, чем линейная.
, то есть кубическая функция более высокого порядка малости, чем линейная.
3) Если ![]() , где
, где ![]() – ненулевая константа, то функции имеют одинаковый порядок малости.
– ненулевая константа, то функции имеют одинаковый порядок малости.
Простейший пример: ![]() , иными словами, карлик
, иными словами, карлик ![]() бежит к нулю строго в два раза медленнее, чем
бежит к нулю строго в два раза медленнее, чем ![]() , и «дистанция» между ними сохраняется постоянной.
, и «дистанция» между ними сохраняется постоянной.
Наиболее интересен частный случай, когда ![]() . Такие функции называют бесконечно малыми эквивалентными функциями.
. Такие функции называют бесконечно малыми эквивалентными функциями.
Перед тем как привести элементарный пример, поговорим о самом термине. Эквивалентность. Данное слово уже встречалось на уроке Методы решения пределов, в других статьях и встретится ещё неоднократно. Что такое эквивалентность? Существует математическое определение эквивалентности, логическое, физическое и т. д., но попытаемся понять саму сущность.
Эквивалентность – это равнозначность (или равноценность) в каком-нибудь отношении. Самое время размять мышцы и немного отдохнуть от высшей математики. Сейчас на улице хороший январский морозец, поэтому очень важно хорошо утеплиться. Пожалуйста, пройдите в прихожую и откройте шкаф с одеждой. Представьте, что там висят два одинаковых тулупа, которые отличаются только цветом. Один оранжевый, другой фиолетовый. С точки зрения своих согревающих качеств, данные тулупы являются эквивалентными. И в первом, и во втором тулупе вам будет одинаково тепло, то есть выбор равноценен, что оранжевый надеть, что фиолетовый – без выигрыша: «один к одному равно одному». Но вот с точки зрения безопасности на дороге тулупы уже не эквивалентны – оранжевый цвет лучше заметен водителям транспорта, …да и патруль не остановит, потому что с обладателем такой одежды и так всё понятно. В этом отношении можно считать, что тулупы «одного порядка малости», условно говоря, «оранжевый тулуп» ![]() в два раза «безопаснее» «фиолетового тулупа»
в два раза «безопаснее» «фиолетового тулупа» ![]() («который хуже, но тоже заметен в темноте»). А если выйти на мороз в одном пиджаке
(«который хуже, но тоже заметен в темноте»). А если выйти на мороз в одном пиджаке и носках, то разница будет уже колоссальной, таким образом, пиджак и тулуп – «разного порядка малости».
…Зашибись, нужно запостить в Википедии со ссылкой на данный урок =) =) =)
Напрашивающийся пример бесконечно малых эквивалентных функций вам хорошо знаком – это функции первого замечательного предела ![]() .
.
Дадим геометрическое истолкование 1-го замечательного предела. Выполним чертёж:
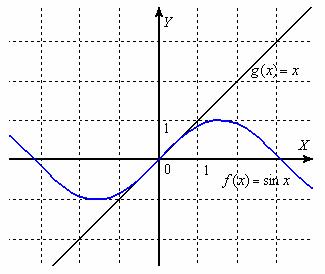
Ну вот, крепкая мужская дружба графиков виднА даже невооруженным взглядом. А бесконечно близко вблизи нуля их и мама родная не отличит. Таким образом, если ![]() , то функции
, то функции ![]() бесконечно малЫ и эквивалентны. А если разница ничтожно мала? Тогда в пределе
бесконечно малЫ и эквивалентны. А если разница ничтожно мала? Тогда в пределе ![]() синус вверху можно заменить «иксом»:
синус вверху можно заменить «иксом»: ![]() , или «икс» внизу синусом:
, или «икс» внизу синусом: ![]() . По сути, получилось геометрическое обоснование первого замечательного предела.
. По сути, получилось геометрическое обоснование первого замечательного предела.
Аналогично, кстати, можно проиллюстрировать любой замечательный предел, который равен единице.
! Внимание! Эквивалентность объектов не подразумевает совпадение объектов! Оранжевый и фиолетовый тулупы эквивалентно теплЫ, но это разные тулупы. Функции ![]() практически неотличИмы вблизи нуля, но это две разные функции.
практически неотличИмы вблизи нуля, но это две разные функции.
Обозначение: эквивалентность обозначается значком «тильда».
Например: ![]() – «синус икса эквивалентен иксу», если
– «синус икса эквивалентен иксу», если ![]() .
.
Из вышесказанного следует очень важный вывод: если две бесконечно малые функции эквивалентны, то одну можно заменить другой. Данный приём широко применяется на практике, и прямо сейчас мы увидим, каким образом:
Замечательные эквивалентности в пределах
Для решения практических примеров потребуется таблица замечательных эквивалентностей. Не многочленом единым жив студент, поэтому поле дальнейшей деятельности будет очень широким. Сначала с помощью теории бесконечно малых эквивалентных функций перещёлкаем примеры первой части урока Замечательные пределы. Примеры решений, в которой были найдены следующие пределы:
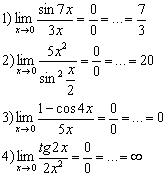
1) Решим предел ![]() . Заменим бесконечно малую функцию числителя
. Заменим бесконечно малую функцию числителя ![]() на эквивалентную бесконечно малую функцию
на эквивалентную бесконечно малую функцию ![]() :
:
![]()
Почему можно провести такую замену? Потому что бесконечно близко вблизи нуля график функции ![]() практически совпадает с графиком функции
практически совпадает с графиком функции ![]() .
.
В этом примере мы использовали табличную эквивалентность ![]() , где
, где ![]() . Удобно, что в качестве параметра «альфа» может выступать не только «икс», но и сложная функция, которая стремится к нулю.
. Удобно, что в качестве параметра «альфа» может выступать не только «икс», но и сложная функция, которая стремится к нулю.
2) Найдём предел 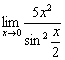 . В знаменателе используем эту же эквивалентность
. В знаменателе используем эту же эквивалентность ![]() , в данном случае
, в данном случае ![]() :
:
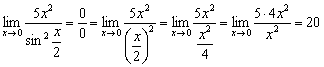
Обратите внимание, что синус изначально находился под квадратом, поэтому на первом шаге ![]() тоже необходимо целиком поместить под квадрат.
тоже необходимо целиком поместить под квадрат.
Не забываем и про теорию: в первых двух примерах получены конечные числа, значит, числители и знаменатели одного порядка малости.
3) Найдём предел ![]() . Заменим бесконечно малую функцию числителя эквивалентной функцией
. Заменим бесконечно малую функцию числителя эквивалентной функцией ![]() , где
, где ![]() :
:
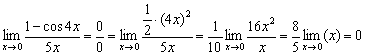
Здесь числитель более высокого порядка малости, чем знаменатель. Лилипут ![]() (и эквивалентный ему лилипут
(и эквивалентный ему лилипут ![]() ) достигает нуля быстрее, чем
) достигает нуля быстрее, чем ![]() .
.
4) Найдём предел ![]() . Заменим бесконечно малую функцию числителя эквивалентной функцией
. Заменим бесконечно малую функцию числителя эквивалентной функцией ![]() , где
, где ![]() :
:
![]()
А здесь, наоборот, знаменатель более высокого порядка малости, чем числитель, карлик ![]() убегает к нулю быстрее карлика
убегает к нулю быстрее карлика ![]() (и эквивалентного ему карлика
(и эквивалентного ему карлика ![]() ).
).
Следует ли использовать замечательные эквивалентности на практике? Следует, но далеко не всегда. Так, решение не очень сложных пределов (наподобие только что рассмотренных) нежелательно решать через замечательные эквивалентности. Вас могут упрекнуть в халтуре и заставить прорешать их стандартным образом с помощью тригонометрических формул и первого замечательного предела. Однако с помощью рассматриваемого инструмента очень выгодно осуществлять проверку решения или даже сразу узнавать правильный ответ. Характерен Пример № 14 урока Методы решения пределов:
![]()
На чистовике целесообразно оформить немаленькое полное решение с заменой переменной. Но готовый ответ лежит на поверхности – мысленно используем эквивалентность ![]() :
: ![]() .
.
И ещё раз геометрический смысл: почему в числителе функцию ![]() допустимо заменить функцией
допустимо заменить функцией ![]() ? Бесконечно близко вблизи нуля их графики можно отличить разве что под мощным микроскопом.
? Бесконечно близко вблизи нуля их графики можно отличить разве что под мощным микроскопом.
Помимо проверки решения, замечательные эквивалентности используются ещё в двух случаях:
– когда пример достаточно сложен или вообще неразрешим обычным способом;
– когда замечательные эквивалентности требуется применить по условию.
Рассмотрим более содержательные задания:
Пример 4
Найти предел
![]()
На повестке дня неопределённость «ноль на ноль» и ситуация погранична: решение можно провести стандартно, но преобразований будет много. С моей точки зрения, здесь вполне уместно использовать замечательные эквивалентности:
![]()
Заменим бесконечно малые функции эквивалентными функциями. При ![]() :
:
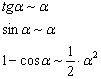
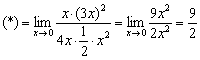
Вот и всё!
Единственный технический нюанс: изначально тангенс находился в квадрате, поэтому после замены аргумент ![]() тоже необходимо возвести в квадрат.
тоже необходимо возвести в квадрат.
Пример 5
Найти предел
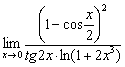
Данный предел разрешим через тригонометрические формулы и замечательные пределы, но решение опять же будет не сильно приятным. Это пример для самостоятельного решения, будьте особенно внимательными в ходе преобразования числителя. Если возникнет путаница со степенями, представьте его в виде произведения: ![]()
Пример 6
Найти предел
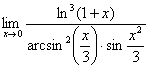
А вот это уже тяжёлый случай, когда провести решение стандартным образом весьма непросто. Используем замечательные эквивалентности:
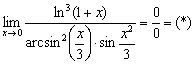
Заменим бесконечно малые эквивалентными. При ![]() :
:
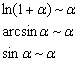
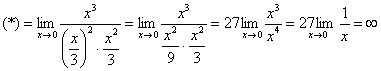
Получена бесконечность, значит, знаменатель более высокого порядка малости, чем числитель.
Резво практика пошла без верхней одежды =)
Пример 7
Найти предел
![]()
Это пример для самостоятельного решения. Подумайте, как разобраться с логарифмом ;-)
Не редкость, когда замечательные эквивалентности используются в комбинации с другими методами решения пределов:
Пример 8
Найти предел функции, используя эквивалентные бесконечно малые величины и другие преобразования
![]()
Заметьте, что здесь требуется применить замечательные эквивалентности по условию.
Решаем:
![]()
На первом шаге используем замечательные эквивалентности. При ![]() :
:
![]()
С синусом всё понятно: ![]() . Что делать с логарифмом? Представим логарифм в виде
. Что делать с логарифмом? Представим логарифм в виде ![]() и применим эквивалентность
и применим эквивалентность ![]() . Как вы понимаете, в данном случае
. Как вы понимаете, в данном случае ![]() и
и ![]()
![]()
На втором шаге применим приём, рассмотренный ещё на уроке Пределы функций. Примеры решений. Умножим числитель и знаменатель на сопряженное выражение:
![]()
Готово.
Пример 9
Найти предел функции, используя эквивалентные бесконечно малые величины и другие преобразования
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Иногда замечательные эквивалентности приходится использовать последовательно – два и даже бОльшее количество раз, когда бесконечно малые эквивалентные функции вложены друг в друга по принципу «матрёшек»:
Пример 10
Найти предел функции с помощью эквивалентных бесконечно малых функций
![]()
Перед решением нужно выполнить предварительные преобразования.
В числителе вынесем за скобки «минус»: ![]() чтобы в дальнейшем воспользоваться эквивалентностью
чтобы в дальнейшем воспользоваться эквивалентностью ![]() .
.
В знаменателе проведём искусственное преобразование ![]() , чтобы далее применить эквивалентность
, чтобы далее применить эквивалентность ![]() . Кстати, запомните это трюк с логарифмом, он используется и в других задачах математического анализа.
. Кстати, запомните это трюк с логарифмом, он используется и в других задачах математического анализа.
Начнём оформлять решение:
![]()
В числителе используем замечательную эквивалентность ![]() . В данном случае
. В данном случае ![]() . Важнейшим моментом является тот факт, что при «икс», стремящемся к нулю,
. Важнейшим моментом является тот факт, что при «икс», стремящемся к нулю, ![]() .
.
В знаменателе ![]() тоже бесконечно малая величина, именно поэтому можно применить эквивалентность
тоже бесконечно малая величина, именно поэтому можно применить эквивалентность ![]() , где
, где ![]() при
при ![]() .
.
![]()
После замены проведена пара технических действий – вынесение «минуса» в знаменателе и сокращение минусов. Неопределённость 0:0 никуда не делась, и есть надобность воспользоваться бесконечно малыми эквивалентными функциями ещё раз. Если ![]() , то
, то ![]() :
:
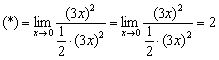
Задачка потолще для самостоятельного решения:
Пример 11
Найти предел функции с помощью эквивалентных бесконечно малых функций
![]()
Нетрудно догадаться, что «матрёшку» следует разбирать в привычном порядке, начиная от «внешней», и заканчивая самой маленькой «внутренней». Полное решение и ответ в конце урока.
Как я уже отмечал, «икс» не обязан стремиться к нулю, он может стремиться к произвольному числу, в том числе и к бесконечности – лишь бы функции были бесконечно малыми, и существовал предел их отношений ![]() . Но практика показывает, что почти во всех заданиях
. Но практика показывает, что почти во всех заданиях ![]() , именно поэтому я и не привёл других примеров.
, именно поэтому я и не привёл других примеров.
Тем не менее, рассмотрим более редкий тип пределов, который встречается, в частности, при исследовании числовых рядов на сходимость:
Пример 12
Найти предел функции
![]()
В данном примере «икс» стремится к бесконечности, и ![]() . Иными словами, функция
. Иными словами, функция ![]() бесконечно малА в точке
бесконечно малА в точке ![]() . Чтобы раскрыть неопределённость
. Чтобы раскрыть неопределённость ![]() целесообразно использовать теорию эквивалентных бесконечно малых величин.
целесообразно использовать теорию эквивалентных бесконечно малых величин.
Поскольку ![]() , то применима замечательная эквивалентность
, то применима замечательная эквивалентность ![]() :
:
![]()
Что и говорить, вкусный способ решения.
Пример 13
Найти предел функции
![]()
Это счастливый заключительный пример для самостоятельного решения. После эквивалентной замены неопределенность ![]() трансформируется в неопределённость
трансформируется в неопределённость ![]() , которая раскрывается по обычной схеме. Если возникли затруднения на завершающем этапе, пожалуйста, вернитесь к первой части урока Методы решения пределов.
, которая раскрывается по обычной схеме. Если возникли затруднения на завершающем этапе, пожалуйста, вернитесь к первой части урока Методы решения пределов.
Что тут сказать…
Всё =)
Решения и ответы:
Пример 5
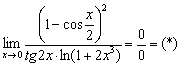
Заменим бесконечно малые функции эквивалентными функциями. При ![]() :
:
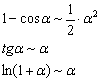
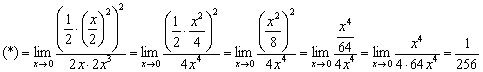
Пример 7
![]()
Представим логарифм в виде ![]() и заменим бесконечно малые эквивалентными. При
и заменим бесконечно малые эквивалентными. При ![]() :
:
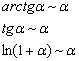
![]()
Здесь числитель более высокого порядка малости, чем знаменатель.
Пример 9
![]()
Используем замечательные эквивалентности. При ![]() :
:
![]()
![]()
Пример 11
![]()
1) Так как ![]() , то применима эквивалентность
, то применима эквивалентность ![]() :
:
![]()
2) Так как ![]() , то применима эквивалентность
, то применима эквивалентность ![]() :
:
![]()
3) Так как ![]() , то применима эквивалентность
, то применима эквивалентность ![]() :
:
![]()
Заменим бесконечно малую функцию эквивалентной:
![]()
![]()
Пример 13
![]()
Заменим бесконечно малую функцию эквивалентной функцией. Если ![]() , то
, то ![]() .
.
![]()
Разделим числитель и знаменатель на ![]() :
:
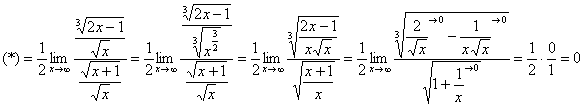
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright