


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как проверить, удовлетворяет ли функция уравнению?
На дворе начало апреля 2015 и эти солнечные, но ещё холодные деньки навеяли ностальгические воспоминания о своих первых, во многом любительских заметках по высшей математике. Но время шло, тараканы взрослели, и мой стиль становился всё более и более академичным, а статьи – всё более объёмными и обстоятельными. Однако, не зря говорят, что всё возвращается на круги своя, и, видимо, поэтому сегодня появилось желание вернуться к той же лёгкости и непринуждённости изложения материала. По крайне мере, я попытаюсь =)
Задание, сформулированное в заголовке статьи, оказалось обойдено вниманием в теме «обычных» производных (производных функции ![]() ), и, прежде чем перейти к примерам с функциями нескольких переменных, наверстаем упущенное:
), и, прежде чем перейти к примерам с функциями нескольких переменных, наверстаем упущенное:
Пример 1
Проверить, удовлетворяет ли функция ![]() уравнению
уравнению ![]()
! Примечание: в условии таких задач производную нередко обозначают через ![]() , и это не должно сбивать с толку!
, и это не должно сбивать с толку!
Решение: поскольку в предложенное уравнение входит не только функция, но и её производная, то сначала следует найти производную:
![]()
Далее решение можно оформить двумя эквивалентными способами:
Стиль №1. Подставим ![]() и
и ![]() в левую часть уравнения и проведём упрощения:
в левую часть уравнения и проведём упрощения:
![]()
![]() – в результате получена правая часть, таким образом, данная функция удовлетворяет данному уравнению.
– в результате получена правая часть, таким образом, данная функция удовлетворяет данному уравнению.
Что это, кстати, значит? Грубо говоря, функция ![]() является корнем уравнения
является корнем уравнения ![]() .
.
Стиль №2. Подставим ![]() и
и ![]() в уравнение и выполним упрощения (в данном случае только левой части):
в уравнение и выполним упрощения (в данном случае только левой части):
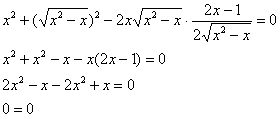
Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.
Аналогичную проверку, разумеется, можно выполнить и для других функций. Так, например, подставим ![]() и её производную
и её производную ![]() в левую часть уравнения (Стиль №1):
в левую часть уравнения (Стиль №1):
![]() – получена правая часть, значит, функция
– получена правая часть, значит, функция ![]() тоже удовлетворяет данному уравнению.
тоже удовлетворяет данному уравнению.
А вот, скажем, функция ![]() «не подходит». И действительно, подставляя
«не подходит». И действительно, подставляя ![]() в уравнение
в уравнение ![]() (Стиль №2):
(Стиль №2):
![]()
![]() – получаем неверное равенство.
– получаем неверное равенство.
Совершенно понятно, что таких «неудовлетворительных» функций – великое множество.
Многие читатели уже давно интуитивно чувствуют нечто знакомое, и это неспроста! Всем с раннего детства знакома ситуация, когда, широко разинув рот, с интересом слушаешь взрослого, после чего там оказывается невкусная таблетка…, а то и вообще шприц в попе =) Вот и сейчас вы побывали в похожей ситуации! – неожиданно так, чтобы испугаться никто не успел, познакомил я вас с одной ужасной вещью:))
![]() – это не что иное, как дифференциальное уравнение, а функция
– это не что иное, как дифференциальное уравнение, а функция ![]() – одно из его решений. Дифференциальные уравнения мы научимся решать позже, а пока что проведём «артподготовку» к этой теме. Самостоятельно:
– одно из его решений. Дифференциальные уравнения мы научимся решать позже, а пока что проведём «артподготовку» к этой теме. Самостоятельно:
Пример 2
Проверить, удовлетворяет ли функция ![]() уравнению
уравнению ![]()
Здесь решение чуть выгоднее провести первым способом, т.е. найти производную и подставить ![]() в левую часть уравнения с дальнейшими преобразованиями.
в левую часть уравнения с дальнейшими преобразованиями.
Пример 3
Проверить, удовлетворяет ли функция ![]() уравнению
уравнению ![]()
В этом же задании подстановка осуществляется в обе части уравнения и по этой причине удобнее использовать 2-й способ, получив верное либо неверное равенство.
Следует отметить, что функция вовсе не обязана удовлетворять уравнению, и иногда приходится давать противоположный ответ: «данная функция НЕ удовлетворяет данному уравнению». Но такой исход всегда неприятен, поскольку начинает мерещиться, что где-то допущена ошибка, после чего следует тщательная проверка, а зачастую и параноидальная перепроверка решения.
Примерные образцы чистового оформления примеров внизу страницы.
Как я уже намекнул в самом начале, рассматриваемое задание значительно чаще формулируется для функции нескольких, а точнее – для функции двух переменных; поэтому данный урок и оказался в разделе ФНП. Предполагается, что на данный момент вы умеете находить частные производные функции двух переменных:
Пример 4
Проверить, удовлетворяет ли функция ![]() уравнению
уравнению ![]()
И сразу обращаю внимание на запись частных производных – в подавляющем большинстве подобных примеров вы встретите именно громоздкие обозначения. В принципе, уравнение можно переписать в виде ![]() и это ни в коем случае не будет ошибкой, но я буду придерживаться традиционного стиля, с которым вы вероятнее всего столкнётесь на практике.
и это ни в коем случае не будет ошибкой, но я буду придерживаться традиционного стиля, с которым вы вероятнее всего столкнётесь на практике.
Решение: в предложенное уравнение входит как сама функция, так и её частные производные первого порядка, что сподвигает к естественным действиям:
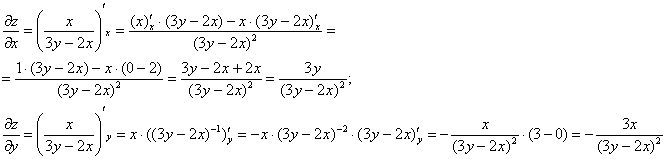
Решение, напоминаю, можно оформить двумя способами, и, на мой взгляд, здесь проще подставить найденные частные производные ![]() в левую часть:
в левую часть:
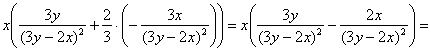
![]() – «на выходе» получена правая часть нашего уравнения.
– «на выходе» получена правая часть нашего уравнения.
Ответ: данная функция удовлетворяет данному уравнению.
Пара примеров для самостоятельного решения:
Пример 5
Проверить, удовлетворяет ли функция ![]() уравнению
уравнению ![]()
Тут сподручнее выполнить подстановку в обе части и получить верное или неверное равенство.
Пример 6
То же задание для функции ![]() и уравнения
и уравнения ![]()
А здесь удобнее упростить левую часть и выяснить, получится ли в итоге ![]() .
.
Предостерегаю от мысли «Да чего тут решать, и так всё понятно». Добросовестно прорешивая примеры, вы не только отрабатываете тематическую задачу, но и шлифуете свою технику нахождения частных производных. И это тем более важно, поскольку я предлагаю вам не абы какие-то задачки, а связный, методически продуманный курс статей – чтобы полученные знания и навыки остались с вами надолго. Таким образом, наш урок вовсе не закончился – он в самом разгаре!
Решения и ответы в подвале.
Помимо частных производных 1-го порядка, в уравнении могут присутствовать и частные производные более высоких порядков, как правило – второго:
Пример 7
Проверить, удовлетворяет ли функция ![]() уравнению
уравнению ![]()
Здесь вместо буквы «зет» использована буква «у», что является весьма распространённым вариантом обозначения функции.
Решение: сначала найдём частные производные 1-го порядка:
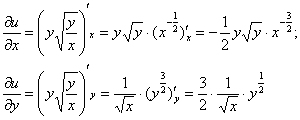
Затем входящие в уравнение частные производные 2-го порядка:
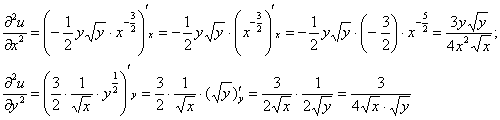
Подставим ![]() и
и ![]() в левую часть уравнения:
в левую часть уравнения:
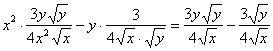 – в результате НЕ получена правая часть данного уравнения.
– в результате НЕ получена правая часть данного уравнения.
Ответ: данная функция не удовлетворяет данному уравнению.
Так действительно бывает!
Интересное задание для самостоятельного решения:
Пример 8
Проверить, удовлетворяет ли функция ![]() уравнению
уравнению ![]()
Краткое решение и ответ в конце урока.
И заключительные примеры посвящены тому же заданию, но с функцией ![]() трёх переменных. Следует отметить, что в «реальном» практическом примере вам вряд ли напишут, скольких переменных дана функция, и этот момент всегда следует прояснять самостоятельно:
трёх переменных. Следует отметить, что в «реальном» практическом примере вам вряд ли напишут, скольких переменных дана функция, и этот момент всегда следует прояснять самостоятельно:
Пример 9
Проверить, удовлетворяет ли функция ![]() уравнению
уравнению 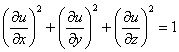
Решение: найдём частные производные 1-го порядка функции трёх переменных:
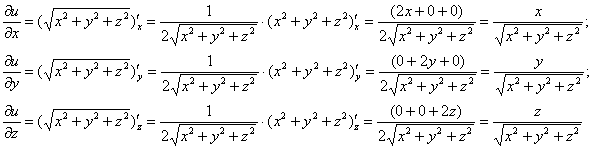
Симметрия это не только красиво – но ещё и очень удобно!
Теперь важно не перепутать квадраты производных с производными второго порядка. Подставим найденные производные в левую часть уравнения:
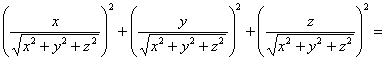
![]() – получена правая часть данного уравнения.
– получена правая часть данного уравнения.
Ответ: дфуду
Вот так и рождаются новые ругательства =)
Симметрия по вашу душу:
Пример 10
Проверить, удовлетворяет ли функция ![]() уравнению
уравнению ![]()
Подумайте, как рациональнее оформить решение.
Дополнительные задания по теме можно найти в задачнике Рябушко (ИДЗ 10.2), ну а я в лучших традициях своего «раннего творчества» отпускаю вас пораньше =) Сейчас ещё раз перечитаю текст и постараюсь избавить его от излишней наукообразной лексики…, хотя наставление в середине статьи всё-таки оставлю, что делать – старею =)
Надеюсь, мои уроки удовлетворяют вашим ожиданиям, и после перемены я жду вас на странице Частные производные неявно заданной функции.
Решения и ответы:
Пример 2: Решение: найдём производную:
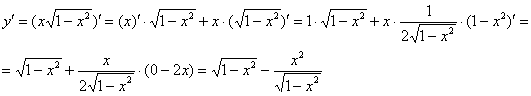
Подставим ![]() и
и ![]() в левую часть уравнения:
в левую часть уравнения:
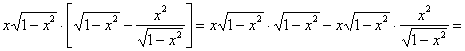
![]() – в результате получена правая часть данного уравнения.
– в результате получена правая часть данного уравнения.
Ответ: данная функция удовлетворяет данному уравнению.
Пример 3: Решение: найдём производную:
![]()
Подставим ![]() и
и ![]() в уравнение
в уравнение ![]() :
:
![]()
Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.
Пример 5: Решение: используя свойства логарифмов, преобразуем функцию:
![]()
Найдём частные производные первого порядка:
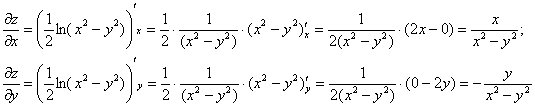
Подставим ![]() и
и ![]() в уравнение
в уравнение ![]() :
:
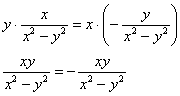
Получено неверное равенство.
Ответ: данная функция не удовлетворяет данному уравнению.
Пример 6: Решение: найдём частные производные первого порядка:
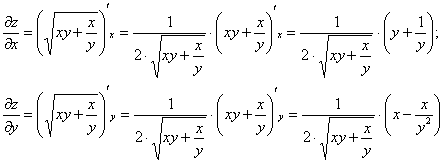
Подставим функцию и найденные производные в левую часть уравнения:
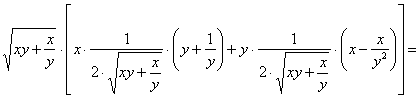
![]() – получена правая часть данного уравнения.
– получена правая часть данного уравнения.
Ответ: данная функция удовлетворяет данному уравнению.
Пример 8: Решение: найдём частную производную по «икс»:
![]() (т.к. константой считается «игрек», то производная берётся от степенной функции)
(т.к. константой считается «игрек», то производная берётся от степенной функции)
Найдём смешанную частную производную 2-го порядка:
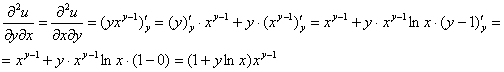
(т.к. константой считается «икс», то производная ![]() берётся как производная от показательной функции)
берётся как производная от показательной функции)
Подставим ![]() и
и ![]() в уравнение:
в уравнение:
![]()
Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.
Пример 10: Решение: преобразуем функцию:
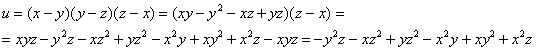
Найдем частные производные первого порядка:
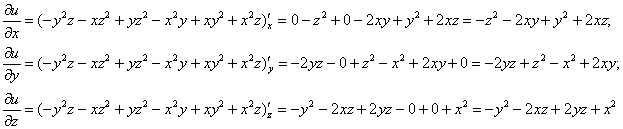
Подставим найденные производные в уравнение ![]() :
:
![]()
Получено верное равенство
Ответ: данная функция удовлетворяет данному уравнению.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright