


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Производные высших порядков
На данном уроке мы научимся находить производные высших порядков, а также записывать общую формулу «энной» производной. Кроме того, будет рассмотрена формула Лейбница ![]() таковой производной и по многочисленным просьбам – производные высших порядков от неявно заданной функции. Предлагаю сразу же пройти мини-тест:
таковой производной и по многочисленным просьбам – производные высших порядков от неявно заданной функции. Предлагаю сразу же пройти мини-тест:
Вот функция: ![]() и вот её первая производная:
и вот её первая производная:
![]()
В том случае, если у вас возникли какие-либо трудности / недопонимание по поводу этого примера, пожалуйста, начните с двух базовых статей моего курса: Как найти производную? и Производная сложной функции. После освоения элементарных производных рекомендую ознакомиться с уроком Простейшие задачи с производной, на котором мы разобрались, в частности со второй производной.
Нетрудно даже догадаться, что вторая производная – это производная от 1-й производной:
![]()
В принципе, вторую производную уже считают производной высшего порядка.
Аналогично: третья производная – это производная от 2-й производной:
![]()
Четвёртная производная – есть производная от 3-й производной:
![]()
Пятая производная: ![]() , и очевидно, что все производные более высоких порядков тоже будут равны нулю:
, и очевидно, что все производные более высоких порядков тоже будут равны нулю:
![]()
Помимо римской нумерации на практике часто используют следующие обозначения:
![]() , производную же «энного» порядка обозначают через
, производную же «энного» порядка обозначают через ![]() . При этом надстрочный индекс нужно обязательно заключать в скобки – чтобы отличать производную от «игрека» в степени.
. При этом надстрочный индекс нужно обязательно заключать в скобки – чтобы отличать производную от «игрека» в степени.
Иногда встречается такая запись: ![]() – третья, четвёртая, пятая, …, «энная» производные соответственно.
– третья, четвёртая, пятая, …, «энная» производные соответственно.
Вперёд без страха и сомнений:
Пример 1
Дана функция ![]() . Найти
. Найти ![]() .
.
Решение: что тут попишешь… – вперёд за четвёртой производной :)
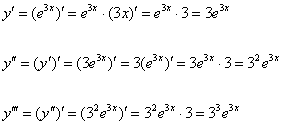
Четыре штриха ставить уже не принято, поэтому переходим на числовые индексы:
![]()
Ответ: ![]()
Хорошо, а теперь задумаемся над таким вопросом: что делать, если по условию требуется найти не 4-ю, а например, 20-ю производную? Если для производной 3-4-5-го (максимум, 6-7-го) порядка решение оформляется достаточно быстро, то до производных более высоких порядков мы «доберёмся» ой как не скоро. Не записывать же, в самом деле, 20 строк! В подобной ситуации нужно проанализировать несколько найденных производных, увидеть закономерность и составить формулу «энной» производной. Так, в Примере 1 легко понять, что при каждом следующем дифференцировании перед экспонентой будет «выскакивать» дополнительная «тройка», причём на любом шаге степень «тройки» равна номеру производной, следовательно:
![]() , где
, где ![]() – произвольное натуральное число.
– произвольное натуральное число.
И действительно, если ![]() , то получается в точности 1-я производная:
, то получается в точности 1-я производная: ![]() , если
, если ![]() – то 2-я:
– то 2-я: ![]() и т. д. Таким образом, двадцатая производная определяется почти мгновенно:
и т. д. Таким образом, двадцатая производная определяется почти мгновенно: ![]() – и никаких «километровых простыней»!
– и никаких «километровых простыней»!
Разогреваемся самостоятельно:
Пример 2
Найти ![]() функции
функции ![]() . Записать производную
. Записать производную ![]() порядка
порядка
Решение и ответ в конце урока.
После бодрящей разминки рассмотрим более сложные примеры, в которых отработаем вышеприведённый алгоритм решения. Тем, кто успел ознакомиться с уроком Предел последовательности, будет чуть легче:
Пример 3
Найти ![]() для функции
для функции ![]() .
.
Решение: чтобы прояснить ситуацию найдём несколько производных:
![]()
Полученные числа перемножать не спешим! ;-)
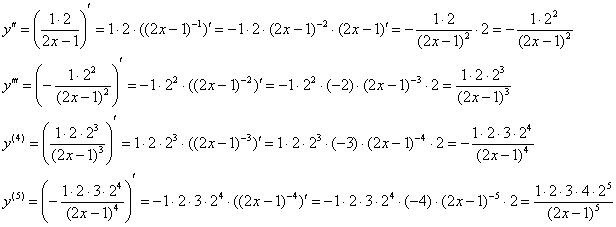
Пожалуй, хватит. …Даже немного переборщил.
На следующем шаге составим формулу «энной» производной (хоть по условию и не нужно). Для этого смотрим на полученные результаты и выявляем закономерности, с которыми получается каждая следующая производная.
Во-первых, они знакочередуются. Знакочередование обеспечивает «мигалка», и поскольку 1-я производная положительна, то в общую формулу войдёт следующий множитель: ![]() . Подойдёт и эквивалентный вариант
. Подойдёт и эквивалентный вариант ![]() , но лично я, как оптимист, люблю знак «плюс» =)
, но лично я, как оптимист, люблю знак «плюс» =)
Во-вторых, в числителе «накручивается» факториал, причём он «отстаёт» от номера производной на одну единицу: ![]()
И в-третьих, в числителе растёт степень «двойки», которая равна номеру производной. То же самое можно сказать о степени знаменателя. Окончательно:
![]()
В целях проверки подставим парочку значений «эн», например, ![]() и
и ![]() :
:
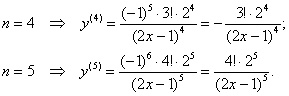
Замечательно, теперь допустить ошибку – просто грех:
![]()
Ответ: ![]()
Более простая функция для самостоятельного решения:
Пример 4
Найти ![]() функции
функции ![]() .
.
И задачка позанятнее:
Пример 5
Найти ![]() функции
функции ![]() .
.
Ещё раз повторим порядок действий:
1) Сначала находим несколько производных. Чтобы уловить закономерности обычно хватает трёх-четырёх.
2) Затем настоятельно рекомендую составить (хотя бы на черновике) «энную» производную – она гарантированно убережёт от ошибок. Но можно обойтись и без ![]() , т. е. мысленно прикинуть и сразу записать, например, двадцатую или восьмую производную. Более того, некоторые люди вообще способны решить рассматриваемые задачи устно. Однако следует помнить, что «быстрые» способы чреваты, и лучше перестраховаться.
, т. е. мысленно прикинуть и сразу записать, например, двадцатую или восьмую производную. Более того, некоторые люди вообще способны решить рассматриваемые задачи устно. Однако следует помнить, что «быстрые» способы чреваты, и лучше перестраховаться.
3) На заключительном этапе выполняем проверку «энной» производной – берём пару значений «эн» (лучше соседних) и выполняем подстановку. А ещё надёжнее – проверить все найденные ранее производные. После чего подставляем в ![]() нужное значение, например,
нужное значение, например, ![]() или
или ![]() и аккуратно причёсываем результат.
и аккуратно причёсываем результат.
Краткое решение 4 и 5-го примеров в конце урока.
В некоторых задачах, во избежание проблем, над функцией нужно немного поколдовать:
Пример 6
Записать формулу производной ![]() порядка для функции
порядка для функции ![]()
Решение: дифференцировать предложенную функцию совсем не хочется, поскольку получится «плохая» дробь, которая сильно затруднит нахождение последующих производных.
В этой связи целесообразно выполнить предварительные преобразования: используем формулу разности квадратов и свойство логарифма ![]() :
:
![]()
Совсем другое дело:
![]()
И старые подруги:
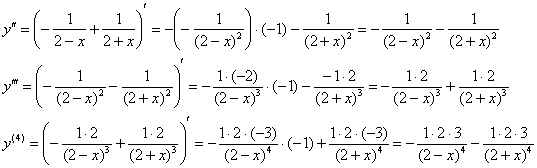
Думаю, всё просматривается. Обратите внимание, что 2-я дробь знакочередуется, а 1-я – нет. Конструируем производную ![]() порядка:
порядка:
![]()
Контроль:
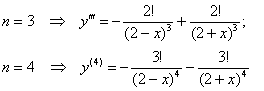
Ну и для красоты вынесем факториал за скобки,
ответ: 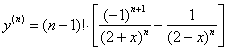
Интересное задание для самостоятельного решения:
Пример 7
Записать формулу производной ![]() порядка для функции
порядка для функции ![]()
Краткое решение и ответ в конце урока.
А сейчас о незыблемой круговой поруке, которой позавидует даже итальянская мафия:
Пример 8
Дана функция ![]() . Найти
. Найти ![]()
Восемнадцатая производная в точке ![]() . Всего-то.
. Всего-то.
Решение: сначала, очевидно, нужно найти ![]() . Поехали:
. Поехали:
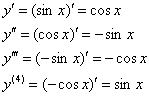
С синуса начинали, к синусу и пришли. Понятно, что при дальнейшем дифференцировании этот цикл будет продолжаться до бесконечности, и возникает следующий вопрос: как лучше «добраться» до восемнадцатой производной?
Способ «любительский»: быстренько записываем справа в столбик номера последующих производных:
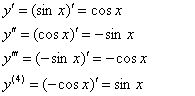

Таким образом: ![]()
Но это работает, если порядок производной не слишком велик. Если же надо найти, скажем, сотую производную, то следует воспользоваться делимостью на 4. Сто делится на 4 без остатка, и легко видеть, что таковые числа располагаются в нижней строке, поэтому: ![]() .
.
Кстати, 18-ю производную тоже можно определить из аналогичных соображений:
во второй строке находятся числа, которые делятся на 4 с остатком 2.
Другой, более академичный метод основан на периодичности синуса и формулах приведения. Пользуемся готовой формулой «энной» производной синуса ![]() , в которую просто подставляется нужный номер. Например:
, в которую просто подставляется нужный номер. Например:
![]() (формула приведения
(формула приведения ![]() );
);
![]() (формула приведения
(формула приведения ![]() )
)
В нашем случае:
![]()
(1) Поскольку синус – это периодическая функция с периодом ![]() , то у аргумента можно безболезненно «открутить» 4 периода (т. е.
, то у аргумента можно безболезненно «открутить» 4 периода (т. е. ![]() ).
).
(2) Пользуемся формулой приведения ![]() .
.
С сотней, к слову, вообще всё элементарно – 25 «оборотов» прочь: ![]()
Заключительная, более лёгкая часть задания – это нахождение восемнадцатой производной в точке:
![]()
Ответ: ![]()
Аналогичная задача для самостоятельного решения.
Пример 9
Дана функция ![]() .
.
Найти ![]() .
.
Кроме того, ориентируясь по таблице формул приведения, постарайтесь самостоятельно получить общую формулу «энной» производной косинуса.
На практике при аргументе синуса либо косинуса часто встречается числовой множитель, например: ![]() . Как находить производные высших порядков в этом случае? Всё будет точно так же (периодичность, формулу приведения), но при каждом дифференцировании перед функцией будет дополнительно «выпрыгивать» «двойка»
. Как находить производные высших порядков в этом случае? Всё будет точно так же (периодичность, формулу приведения), но при каждом дифференцировании перед функцией будет дополнительно «выпрыгивать» «двойка»
Второй параграф посвящён
производным высших порядков от произведения функций 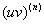
Материал разберём на конкретной задаче:
Пример 10
Найти ![]() функции
функции ![]()
Решение начнём с ключевого вопроса: как выгоднее всего найти третью производную от произведения функций?
…А почему бы, собственно, не взять три производные подряд? Тем более это представляется вполне подъёмной задачей. Используем правило дифференцирования произведения ![]() и упрощаем результат:
и упрощаем результат:
![]()
Со второй производной дела обстоят похуже, но всё-таки ещё не так плохи:
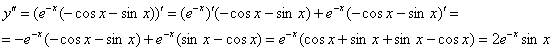
С третьей немножко повезло:
![]()
Всё выглядит весьма благонадёжно, но…
В чём недостаток такого решения? Во-первых, оно длинное. А ведь предложенная функция даже без «наворотов». И, во-вторых, тут легко запутаться (особенно в знаках). Рассмотрим простой и чёткий способ решения подобных заданий:
Формула Лейбница
Пожалуйста, не путайте с более известной формулой Ньютона-Лейбница!
Производную ![]() порядка от произведения двух функций можно найти по формуле:
порядка от произведения двух функций можно найти по формуле:
![]()
В частности:
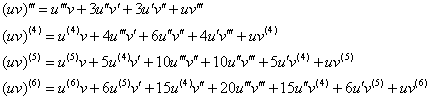
Примечание: здесь и далее предполагается дифференцируемость функций нужное количество раз
Специально запоминать ничего не надо, ибо, чем больше формул знаешь – тем меньше понимаешь. Гораздо полезнее ознакомиться с биномом Ньютона, поскольку формула Лейбница очень и очень на него похожа. Ну а те везунчики, которым достанется производная 7-го либо более высоких порядков (что, правда, маловероятно), будут вынуждены это сделать. Впрочем, когда черёд дойдёт до комбинаторики – то всё равно придётся =)
Найдём третью производную функции ![]() . Используем формулу Лейбница:
. Используем формулу Лейбница:
![]()
В данном случае: ![]() . Производные легко перещёлкать устно:
. Производные легко перещёлкать устно:

Теперь аккуратно и ВНИМАТЕЛЬНО выполняем подстановку и упрощаем результат:
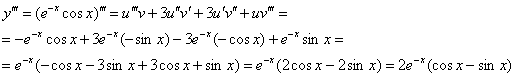
Ответ: ![]()
Аналогичное задание для самостоятельного решения:
Пример 11
Найти ![]() функции
функции ![]()
Если в предыдущем примере решение «в лоб» ещё конкурировало с формулой Лейбница, то здесь оно уже будет действительно неприятным. И ещё неприятнее – в случае более высокого порядка производной:
Пример 12
Найти производную указанного порядка
![]()
Решение: первое и существенное замечание – решать вот так, наверное, не нужно =) =)
Запишем функции ![]() и найдём их производные до 5-го порядка включительно. Предполагаю, что производные правого столбца стали для вас устными:
и найдём их производные до 5-го порядка включительно. Предполагаю, что производные правого столбца стали для вас устными:

В левом же столбце «живые» производные быстро «закончились» и это очень хорошо – в формуле Лейбница обнулятся три слагаемых:
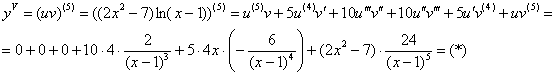
Вновь остановлюсь на дилемме, которая фигурировала в статье о сложных производных: упрощать ли результат? В принципе, можно оставить и так – преподавателю будет даже легче проверять. Но он может потребовать довести решение «до ума». С другой стороны, упрощение по собственной инициативе чревато алгебраическими ошибками. Однако у нас есть ответ, полученный «первобытным» способом =) (см. ссылку в начале решения), и я надеюсь, он правильный:
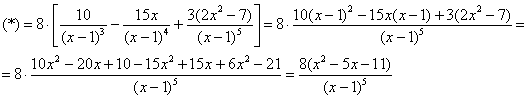
Отлично, всё сошлось.
Ответ: ![]()
Счастливое задание для самостоятельного решения:
Пример 13
Для функции ![]() :
:
а) найти ![]() непосредственным дифференцированием;
непосредственным дифференцированием;
б) найти ![]() по формуле Лейбница;
по формуле Лейбница;
в) вычислить ![]() .
.
Нет, я вовсе не садист – пункт «а» здесь достаточно прост =)
А если серьёзно, то «прямое» решение последовательным дифференцированием тоже имеет «право на жизнь» – в ряде случаев его сложность сопоставима со сложностью применения формулы Лейбница. Используйте, если сочтёте целесообразным – это вряд ли будет основанием для незачёта задания.
Краткое решение и ответ в конце урока.
Чтобы поднять заключительный параграф нужно уметь дифференцировать неявные функции:
Производные высших порядков от функций, заданных неявно
Многие из нас потратили долгие часы, дни и недели жизни на изучение окружностей, парабол, гипербол – а иногда это вообще казалось сущим наказанием. Так давайте же отомстим и продифференцируем их как следует!
Начнём со «школьной» параболы в её каноническом положении:
Пример 14
Дано уравнение ![]() . Найти
. Найти ![]() .
.
Решение: первый шаг хорошо знаком:
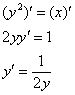
То, что функция и её производная выражены неявно, сути дела не меняет, вторая производная – это производная от 1-й производной:
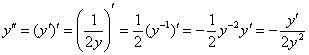
Однако свои правила игры существуют: производные 2-го и более высоких порядков принято выражать только через «икс» и «игрек». Поэтому в полученную 2-ю производную подставим ![]() и избавимся от трёхэтажности дроби:
и избавимся от трёхэтажности дроби:
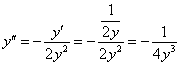
Третья производная – есть производная от 2-й производной:
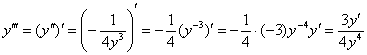
Аналогично, подставим ![]() :
:
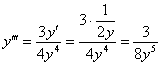
Ответ: ![]()
Симпатичная гипербола – для самостоятельной работы:
Пример 15
Дано уравнение ![]() . Найти
. Найти ![]() .
.
Повторяю, что 2-ю производную и результат следует выразить только через «икс» / «игрек»!
Краткое решение и ответ в конце урока.
После детских шалостей посмотрим немецкую поpнoгр@фию рассмотрим более взрослые примеры, из которых узнаем ещё один важный приём решения:
Пример 16
Найти ![]()
![]()
Эллипс собственной персоной.
Решение: найдём 1-ю производную:
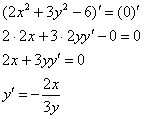
А теперь остановимся и проанализируем следующий момент: сейчас предстоит дифференцировать дробь, что совсем не радует. В данном случае она, конечно, проста, но в реально встречающихся задачах таких подарков раз два и обчёлся. Существует ли способ избежать нахождения громоздкой производной? Существует! Берём уравнение ![]() и используем тот же самый приём, что и при нахождении 1-й производной – «навешиваем» штрихи на обе части:
и используем тот же самый приём, что и при нахождении 1-й производной – «навешиваем» штрихи на обе части:
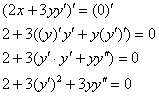
Вторая производная должна быть выражена только через ![]() и
и ![]() , поэтому сейчас (именно сейчас) удобно избавиться от 1-й производной. Для этого в полученное уравнение подставим
, поэтому сейчас (именно сейчас) удобно избавиться от 1-й производной. Для этого в полученное уравнение подставим ![]() :
:
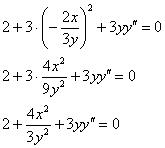
Чтобы избежать лишних технических трудностей, умножим обе части на ![]() , избавляясь тем самым от дроби::
, избавляясь тем самым от дроби::
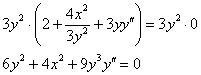
И только на завершающем этапе оформляем дробь:
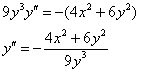
Теперь смотрим на исходное уравнение ![]() и замечаем, что полученный результат поддаётся упрощению:
и замечаем, что полученный результат поддаётся упрощению:
![]()
Ответ: ![]()
Как найти значение 2-й производной в какой-либо точке (которая, понятно, принадлежит эллипсу), например, в точке ![]() ? Очень легко! Этот мотив уже встречался или ещё встретится вам на уроке об уравнении нормали: в выражение 2-й производной нужно подставить
? Очень легко! Этот мотив уже встречался или ещё встретится вам на уроке об уравнении нормали: в выражение 2-й производной нужно подставить ![]() :
:
![]()
Безусловно, во всех трёх случаях (Примеры 14-16) можно получить явно заданные функции и дифференцировать их, но тогда морально настройтесь работать с двумя функциями, которые содержат корни. На мой взгляд, решение удобнее провести «неявным путём».
Заключительный пример для самостоятельного решения:
Пример 17
Найти ![]() неявно заданной функции
неявно заданной функции
![]()
Краткое решение и ответ совсем близко.
Дополнительные примеры повышенной технической сложности можно найти в ИДЗ-6.2 задачника Рябушко. Время от времени меня упрекают в том, что я разбираю слишком много простых задач, однако и в этот урок я намеренно не стал включать примеры со «страшными» производными – моя цель состояла в том, чтобы рассказать о методах и приёмах решения. Главное – хоть небольшое, но понимание, а остальное приложится!
Позабытыми остались и производные высших порядков от параметрически заданных функций, которые практически не встречаются. …А если и встретятся, то, что в них сложного? Вот формулы: ![]() , которые при более или менее приличных навыках можно вывести, не заглядывая ни в какие справочники.
, которые при более или менее приличных навыках можно вывести, не заглядывая ни в какие справочники.
Успехов!
Решения и ответы:
Пример 2. Решение: найдём пятую производную:
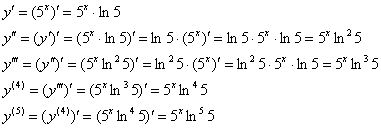
Очевидно, что ![]()
Ответ:![]()
Пример 4. Решение: найдём несколько производных:
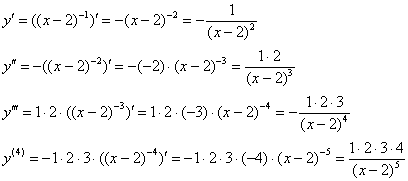
Запишем «энную» производную: ![]()
Таким образом: ![]()
Ответ: ![]()
Пример 5. Решение: найдём несколько производных:
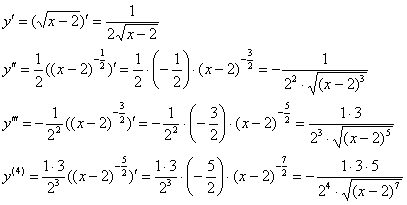
Запишем производную ![]() порядка для
порядка для ![]() :
:
![]()
Таким образом: ![]()
Ответ: ![]()
Примечание: «энную» производную также можно записать с двойным факториалом: ![]() . В частности:
. В частности: ![]() . О том, что такое двойной факториал, читайте в статье Ряды повышенной сложности (после Примера 13).
. О том, что такое двойной факториал, читайте в статье Ряды повышенной сложности (после Примера 13).
Пример 7. Решение: преобразуем функцию:
![]()
Найдём несколько производных:
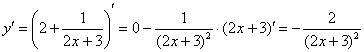
Примечание: производную можно найти и без преобразований с помощью правила 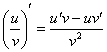 .
.
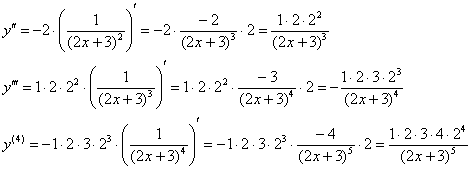
Ответ: ![]()
Пример 9. Решение: найдём несколько производных:
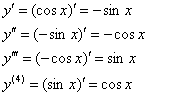

47 делится на 4 с остатком 3 – данному случаю соответствуют производные 3-й строки, таким образом: ![]()
Способ второй: используем формулу ![]() :
:
![]()
Примечание: в силу периодичности косинуса, «убрали» 11 периодов, далее – использовали формулу приведения ![]() .
.
Вычислим производную в точке:
![]()
Ответ: ![]()
Пример 11. Решение: используем формулу Лейбница: ![]()
![]() .
.

Таким образом:
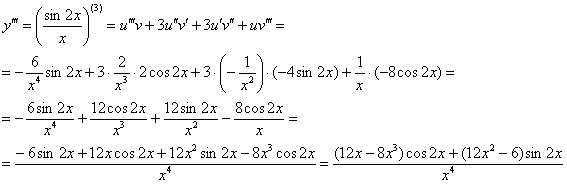
Ответ: ![]()
Пример 13. Решение:
а) найдём 4-ю производную последовательным дифференцированием:
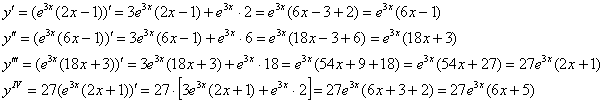
б) найдём 4-ю производную с помощью формулы Лейбница:

Таким образом:
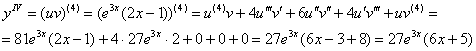
в) ![]()
Ответ: ![]()
Пример 15. Решение: найдём 1-ю производную:
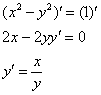
Вторая производная:
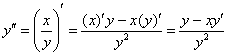 – подставим в неё
– подставим в неё ![]() :
:
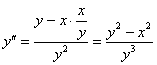
2-ю производную можно упростить: преобразуем исходное уравнение:
![]() – подставим во 2-ю производную:
– подставим во 2-ю производную:
![]()
Найдём третью производную:
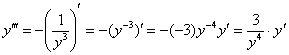 – и подставим в неё
– и подставим в неё ![]() :
:
![]()
Ответ: ![]()
Пример 17. Решение: найдём 1-ю производную:
![]()
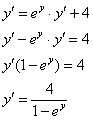
Найдём 2-ю производную:
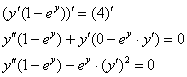
Подставим ![]() :
:
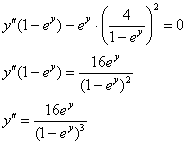
Cпособ второй:
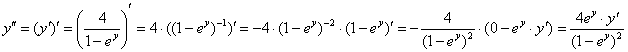 – подставим в неё
– подставим в неё ![]() :
:
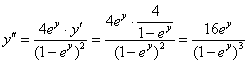
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright