


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Формулы деления отрезка в данном отношении.
Формулы координат середины отрезка
Прошло совсем немного времени, с того момента, когда пилотным выпуском появилась моя первая статья по аналитической геометрии – Векторы для чайников. Затем последовал важный урок Скалярное произведение векторов, а также Линейная (не) зависимость векторов. Базис векторов и Векторное и смешанное произведение векторов. После кропотливого труда я вдруг заметил, что размеры веб страниц достаточно велики, и если так пойдёт дальше, то можно тихо мирно озвереть =) Поэтому предлагаю вашему вниманию небольшое эссе, посвященное очень распространённой геометрической задаче – о делении отрезка в данном отношении, и, как частный случай, о делении отрезка пополам.
Данная задача по тем или иным причинам не вписалась в другие уроки, но зато сейчас есть прекрасная возможность рассмотреть её подробно и неторопливо. Приятная новость состоит в том, что мы немного отдохнём от векторов и сконцентрируем внимание на точках и отрезках.
Формулы деления отрезка в данном отношении
Понятие деления отрезка в данном отношении
Понятие деления отрезка в данном отношении
Нередко обещанного вовсе ждать не приходится, сразу рассмотрим пару точек ![]() и, очевидное невероятное – отрезок
и, очевидное невероятное – отрезок ![]() :
:
![]()
Рассматриваемая задача справедлива, как для отрезков плоскости, так и для отрезков пространства. То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.
Что будем делать с данным отрезком? На этот раз пилить. Кто-то пилит бюджет, кто-то пилит супруга, кто-то пилит дрова, а мы начнём пилить отрезок на две части. Отрезок ![]() делится на две части с помощью некоторой точки
делится на две части с помощью некоторой точки ![]() , которая, понятно, расположена прямо на нём:
, которая, понятно, расположена прямо на нём:

В данном примере точка ![]() делит отрезок
делит отрезок ![]() ТАКИМ образом, что отрезок
ТАКИМ образом, что отрезок ![]() в два раза короче отрезка
в два раза короче отрезка ![]() . ЕЩЁ можно сказать, что точка
. ЕЩЁ можно сказать, что точка ![]() делит отрезок
делит отрезок ![]() в отношении
в отношении ![]() («один к двум»), считая от вершины
(«один к двум»), считая от вершины ![]() .
.
На сухом математическом языке этот факт записывают следующим образом: ![]() , или чаще в виде привычной пропорции:
, или чаще в виде привычной пропорции: ![]() . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае:
. Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае: ![]() .
.
Пропорцию несложно составить и в другом порядке: ![]() – сия запись означает, что отрезок
– сия запись означает, что отрезок ![]() в два раза длиннее отрезка
в два раза длиннее отрезка ![]() , но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.
, но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.
Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:

Здесь справедливо соотношение: ![]() . Если составить пропорцию наоборот, тогда получаем:
. Если составить пропорцию наоборот, тогда получаем: ![]() .
.
После того, как мы разобрались, что значит разделить отрезок в данном отношении, перейдём к рассмотрению практических задач.
Формулы деления отрезка в данном отношении на плоскости
Если известны две точки плоскости ![]() , то координаты точки
, то координаты точки ![]() , которая делит отрезок
, которая делит отрезок ![]() в отношении
в отношении ![]() , выражаются формулами:
, выражаются формулами:
![]()
Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы строго выводятся с помощью векторов (куда ж без них? =)). Кроме того, они справедливы не только для декартовой системы координат, но и для произвольной аффинной системы координат (см. урок Линейная (не) зависимость векторов. Базис векторов). Такая вот универсальная задача.
Пример 1
Найти координаты точки ![]() , делящей отрезок
, делящей отрезок ![]() в отношении
в отношении ![]() , если известны точки
, если известны точки ![]()
Решение: В данной задаче ![]() . По формулам деления отрезка в данном отношении, найдём точку
. По формулам деления отрезка в данном отношении, найдём точку ![]() :
:
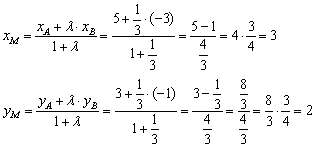
Ответ: ![]()
Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от многоэтажности дроби и проводим окончательные упрощения.
В задаче не требуется строить чертежа, но его всегда полезно выполнить на черновике:
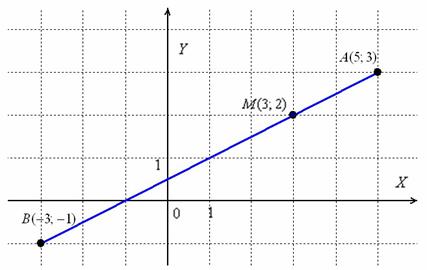
Действительно, соотношение ![]() выполняется, то есть отрезок
выполняется, то есть отрезок ![]() в три раза короче отрезка
в три раза короче отрезка ![]() . Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
. Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
Равноценен второй способ решения: в нём отсчёт начинается с точки ![]() и справедливым является отношение:
и справедливым является отношение: ![]() (человеческими словами, отрезок
(человеческими словами, отрезок ![]() в три раза длиннее отрезка
в три раза длиннее отрезка ![]() ). По формулам деления отрезка в данном отношении:
). По формулам деления отрезка в данном отношении:
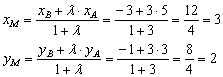
Ответ: ![]()
Заметьте, что в формулах необходимо переместить координаты точки ![]() на первое место, поскольку маленький триллер начинался именно с неё.
на первое место, поскольку маленький триллер начинался именно с неё.
Также видно, что второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке. Например, если по условию дан отрезок ![]() , то предполагается, что вы составите пропорцию
, то предполагается, что вы составите пропорцию ![]() , если дан отрезок
, если дан отрезок ![]() , то «негласно» подразумевается пропорция
, то «негласно» подразумевается пропорция ![]() .
.
А 2-й способ я привёл по той причине, что частенько условие задачи пытаются намеренно подзапутать. Именно поэтому очень важно выполнять черновой чертёж чтобы, во-первых, правильно проанализировать условие, а, во-вторых, в целях проверки. Обидно допускать ошибки в такой простой задаче.
Пример 2
Даны точки ![]() . Найти:
. Найти:
а) точку ![]() , делящую отрезок
, делящую отрезок ![]() в отношении
в отношении ![]() ;
;
б) точку ![]() , делящую отрезок
, делящую отрезок ![]() в отношении
в отношении ![]() .
.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Иногда встречаются задачи, где неизвестен один из концов отрезка:
Пример 3
Точка ![]() принадлежит отрезку
принадлежит отрезку ![]() . Известно, что отрезок
. Известно, что отрезок ![]() в два раза длиннее отрезка
в два раза длиннее отрезка ![]() . Найти точку
. Найти точку ![]() , если
, если ![]() .
.
Решение: Из условия следует, что точка ![]() делит отрезок
делит отрезок ![]() в отношении
в отношении ![]() , считая от вершины
, считая от вершины ![]() , то есть, справедлива пропорция:
, то есть, справедлива пропорция: ![]() . По формулам деления отрезка в данном отношении:
. По формулам деления отрезка в данном отношении:
![]()
Сейчас нам неизвестны координаты точки ![]() :
: ![]() , но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:
, но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:
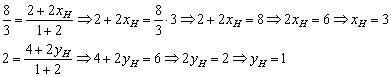
Ответ: ![]()
Для проверки можно взять концы отрезка ![]() и, пользуясь формулами в прямом порядке, убедиться, что при соотношении
и, пользуясь формулами в прямом порядке, убедиться, что при соотношении ![]() действительно получится точка
действительно получится точка ![]() . И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:
. И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:
Пример 4
Точка ![]() . Отрезок
. Отрезок ![]() в полтора раза короче отрезка
в полтора раза короче отрезка ![]() . Найти точку
. Найти точку ![]() , если известны координат точек
, если известны координат точек ![]() .
.
Решение в конце урока. Оно, кстати, не единственное, если пойдёте отличным от образца путём, то это не будет ошибкой, главное, чтобы совпали ответы.
Формулы деления отрезка в данном отношении в пространстве
Для пространственных отрезков всё будет точно так же, только добавится ещё одна координата.
Если известны две точки пространства ![]() , то координаты точки
, то координаты точки ![]() , которая делит отрезок
, которая делит отрезок ![]() в отношении
в отношении ![]() , выражаются формулами:
, выражаются формулами:
![]() .
.
Пример 5
Даны точки ![]() . Найти координаты точки
. Найти координаты точки ![]() , принадлежащей отрезку
, принадлежащей отрезку ![]() , если известно, что
, если известно, что ![]() .
.
Решение: Из условия следует отношение: ![]() . Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость (вдруг кто споткнётся) – пропорцию в условии рациональнее было записать так:
. Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость (вдруг кто споткнётся) – пропорцию в условии рациональнее было записать так: ![]() .
.
По формулам координат середины отрезка:
![]()
Ответ: ![]()
Трёхмерные чертежи в целях проверки выполнять значительно сложнее. Однако всегда можно сделать схематический рисунок, чтобы разобраться хотя бы в условии – какие отрезки нужно соотносить.
Что касается дробей в ответе, не удивляйтесь, обычное дело. Много раз говорил, но повторюсь: в высшей математике принято орудовать обыкновенными правильными и неправильными дробями. Ответ в виде ![]() пойдёт, но вариант с неправильными дробями более стандартен.
пойдёт, но вариант с неправильными дробями более стандартен.
Разминочная задача для самостоятельного решения:
Пример 6
Даны точки ![]() . Найти координаты точки
. Найти координаты точки ![]() , если известно, что она делит отрезок
, если известно, что она делит отрезок ![]() в отношении
в отношении ![]() .
.
Решение и ответ в конце урока. Если трудно сориентироваться в пропорциях, выполните схематический чертёж.
В самостоятельных и контрольных работах рассмотренные примеры встречаются как сами по себе, так и составной частью более крупных задач. В этом смысле типична задача нахождения центра тяжести треугольника.
Разновидность задания, где неизвестен один из концов отрезка, разбирать не вижу особого смысла, так как всё будет похоже на плоский случай, разве что вычислений чуть больше. Лучше вспомним годы школьные:
Формулы координат середины отрезка
Даже неподготовленные читатели могут помнить, как разделить отрезок пополам. Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:

В этот торжественный час стучат барабаны, приветствуя знаменательную пропорцию ![]() . И общие формулы
. И общие формулы ![]() чудесным образом преображаются в нечто знакомое и простое:
чудесным образом преображаются в нечто знакомое и простое:
![]()
Удобным моментом является тот факт, что координаты концов отрезка можно безболезненно переставить:
![]()
В общих формулах такой роскошный номер, как понимаете, не проходит. Да и здесь в нём нет особой надобности, так, приятная мелочь.
Для пространственного случая справедлива очевидная аналогия. Если даны концы отрезка ![]() , то координаты его середины
, то координаты его середины ![]() выражаются формулами:
выражаются формулами:
![]()
Пример 7
Параллелограмм ![]() задан координатами своих вершин
задан координатами своих вершин ![]() . Найти точку пересечения его диагоналей.
. Найти точку пересечения его диагоналей.
Решение: Желающие могут выполнить чертёж. Граффити особенно рекомендую тем, кто капитально забыл школьный курс геометрии.
По известному свойству, диагонали параллелограмма своей точкой пересечения ![]() делятся пополам, поэтому задачу можно решить двумя способами.
делятся пополам, поэтому задачу можно решить двумя способами.
Способ первый: Рассмотрим противоположные вершины ![]() . По формулам деления отрезка пополам найдём середину диагонали
. По формулам деления отрезка пополам найдём середину диагонали ![]() :
:
![]()
В результате: ![]()
Способ второй: Рассмотрим противоположные вершины ![]() . По формулам деления отрезка пополам найдём середину диагонали
. По формулам деления отрезка пополам найдём середину диагонали ![]() :
:
![]()
Таким образом: ![]()
Ответ: ![]()
Пространственный отрезок для самостоятельного решения:
Пример 8
Даны точки ![]() . Найти середину
. Найти середину ![]() отрезка
отрезка ![]() .
.
Вычисления не самые простые получились, числа с ходу придумал. Решение в конце урока.
Как видите, задача деления отрезка пополам настолько прозрачна, что доступна и пятикласснику. На практике середину отрезка чаще всего находят, чтобы составить уравнение медианы треугольника. Но это уже тема другой статьи
Не вижу смысла открывать трёхлитровую банку примеров, поэтому заключительный аккорд урока – случай, когда известна середина отрезка и один из его концов:
Пример 9
Точка ![]() делит отрезок
делит отрезок ![]() пополам. Найти точку
пополам. Найти точку ![]() , если известны точки
, если известны точки ![]()
Решение: Используем формулы координат середины отрезка:
![]()
Нам неизвестны координаты ![]() . И снова можно вывести общую формулу для их нахождения, но гораздо легче сразу подставить числа. Только пропорциями верти:
. И снова можно вывести общую формулу для их нахождения, но гораздо легче сразу подставить числа. Только пропорциями верти:
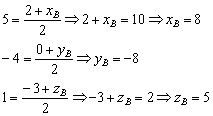
Ответ: ![]()
Проверка выполняется даже устно: берём концы отрезка ![]() и находим его середину.
и находим его середину.
Удачного распила!
Решения и ответы:
Пример 2: Решение:
а) ![]() . Используем формулы деления отрезка в данном отношении:
. Используем формулы деления отрезка в данном отношении:
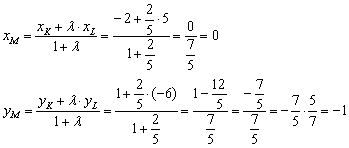
Ответ: ![]()
б) ![]() . Используем формулы деления отрезка в данном отношении:
. Используем формулы деления отрезка в данном отношении:
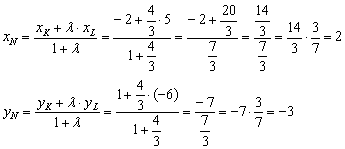
Ответ: ![]()
Пример 4: Решение: Используем формулы деления отрезка в данном отношении:
![]()
Из условия следует, что ![]() .
.
Примечание: формулировка условия «отрезок ![]() в полтора раза короче отрезка
в полтора раза короче отрезка ![]() » эквивалентна формулировке «отрезок
» эквивалентна формулировке «отрезок ![]() в полтора раза длиннее отрезка
в полтора раза длиннее отрезка ![]() », именно из этих соображений и составлена пропорция.
», именно из этих соображений и составлена пропорция.
По условию ![]() , таким образом:
, таким образом:
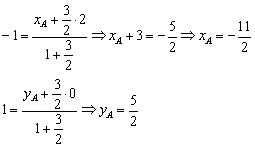
Ответ: ![]()
Пример 6: Решение: Используем формулы деления отрезка в данном отношении:
![]()
В данной задаче ![]() .
.
Таким образом:
![]()
Ответ: ![]()
Пример 8: Решение: Используем формулы координат середины отрезка:
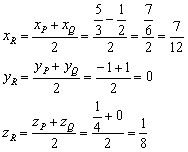
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright