Признаки сходимости несобственных интегралов второго рода

Продолжаем исследование сходимости несобственных интегралов. В первой части урока (см. по ссылке) мы рассмотрели интегралы 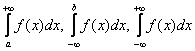(1-го рода), и сейчас изучим признаки сходимости несобственных интегралов второго рода. Эти признаки аналогичны, но вот их применение – это нечто, равнодушным не оставит никого!

Напоминаю, что интеграл 2-го рода имеет вид 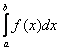, где подынтегральная функция терпит бесконечный разрыв в точке или , и поскольку я правша, то пусть это будет точка :)

Признак сравнения: пусть две неотрицательные функции непрерывны на полуинтервале и для всех этого промежутка выполнено неравенство . Тогда справедливы следующие утверждения:

1) если интеграл 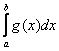сходится, то сходиться будет и интеграл ;
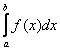2) если интеграл 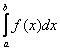расходится, то расходится и интеграл .

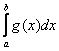Геометрия этих двух случаев очевидна. 1) Если интеграл 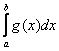сходится, то «серая» площадь конечна. В силу неравенства , интегралу 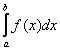соответствует «красная» часть этой конечной площади, и поэтому он тоже сходится:
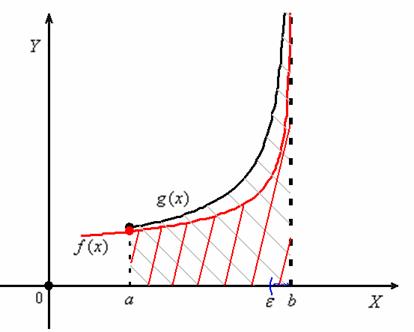
Иллюстрация признака сходимости интеграла 2-го рода с точкой разрыва справа
2) Если интеграл 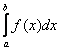расходится, то «красная» площадь бесконечна. И поскольку она является частью «серой» площади, то последняя тоже бесконечна, то есть, интеграл 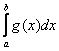будет расходиться.

Следует отметить, что в практических заданиях неравенство может выполняться и не для всех предложенного промежутка – важно чтобы существовала «синяя» - окрестность точки (пусть очень малая), в которой это неравенство справедливо. Иными словами, сходимость или расходимость интеграла зависит от верхнего бесконечного «хвоста».

Рассмотрим простенький интеграл . Прежде всего, отметим, что подынтегральная функция положительна, терпит бесконечный разрыв в точке и непрерывна на промежутке .

! Последний факт очень важен и его проверка – совсем не пустая формальность. На промежутке интегрирования может оказаться две или даже бОльшее количество точек разрыва, и тогда интеграл придётся разделить на части.

Сходимость данного интеграла устанавливается элементарно:
,
и теперь поставим задачу исследовать сходимость похожего интеграла . Понятно, что он тоже вычисляется с пол тычка, но сейчас нам нужно отработать использование признака сравнения, а сделать это лучше на простых примерах.

Рассуждать можно двумя способами. Способ первый. Для степеней с одинаковым основанием и показателями справедливы следующие факты:

– если , то , например: или – тот, кто сомневается, может проверить на калькуляторе;
– и если , то , например, или .

Запишите это к себе на листок!

В нашем интеграле на промежутке подкоренное выражение принимает следующие значения: . Вы согласны? И поэтому:

, а бОльшим знаменателям соответствуют мЕньшие дроби:
, значит, по признаку сравнения исследуемый интеграл сходится вместе с интегралом .

Недостаток этого способа состоит в том, что желаемое неравенство может выполняться далеко не на всём промежутке интегрирования, так, например, для интеграла 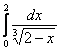на участке от 0 до 1 построенное выше неравенство становится неверным, и поэтому по строгости, здесь нужно разделить пациента на две части: 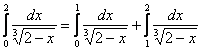, и сказать о том, что первый кусок сходится, т.к. является обычным определённым интегралом.

Но есть второй, более хитрый способ рассуждения – это построение неравенства для ситуации, когда «икс» стремится к двум слева: . Ибо, как я отметил выше, сходимость или расходимость интеграла зависит от поведения бесконечного «хвоста» вблизи точки разрыва.

И мы оформляем решение так:

При :

, следовательно:
, значит, по признаку сравнения, интеграл 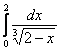сходится вместе с интегралом .

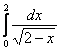Всё!

Хитрость здесь в том, что признак сравнения мы применили в достаточно малой окрестности точки разрыва, и этого вполне достаточно.

Теперь другой случай использования признака – когда в силу того же неравенства из расходимости интеграла 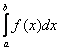следует расходимость 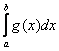. Рассмотрим интеграл , который расходится:

и поставим задачу исследовать сходимость интеграла .

На промежутке интегрирования: , и поэтому по свойству степеней:
, а мЕньшим знаменателям соответствуют бОльшие дроби:
, значит, по признаку сравнения исследуемый интеграл расходится вместе с интегралом .

Альтернативное оформление таково:

При :

, следовательно:
– с тем же самым выводом.

Этот вариант удобен, когда неравенство выполнено не для всех «икс» из промежутка интегрирования, например, при исследовании интеграла .

Точно такой же признак сравнения можно сформулировать для «зеркальной» ситуации, когда подынтегральная функция непрерывна на полуинтервале и терпит бесконечный разрыв в точке . Чертёж уж рисовать не буду – на нём всё так же, только бесконечный «хвост» у левого конца промежутка. Разбираемся самостоятельно, продолжаю нумерацию предыдущей статьи:

Пример 8

Вычислить интегралы 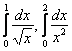и на основании полученных результатов исследовать сходимость интегралов: а) , б)

Краткие доказательства и комментарии в конце урока.

Ну и, наверное, вы уже подметили, что интегралы вида 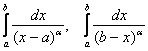, сходятся при и расходятся, если . Заметим заодно, что при всё хозяйство переезжает в числитель, и интеграл перестаёт быть несобственным.

Добавьте это в свой справочник!

Эта «пачка» эталонных интегралов активно используется в практических исследованиях:

Пример 9

Исследовать сходимость интеграла

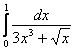
Решение: подынтегральная функция положительна, непрерывна на и терпит единственный бесконечный разрыв слева. Не забываем проверить эти важные факты! – в последующих заданиях такая проверка будет подразумеваться по умолчанию

В знаменателе находится куб и квадратный корень, и возникает вопрос, с чего начать рассуждение? Если при исследовании несобственных интегралов 1-го рода мы ориентировались на старшие степени, то здесь всё наоборот. Сравним данный интеграл со сходящимся интегралом . Если (икс стремится к нулю справа), то:
, а бОльшим знаменателям соответствуют мЕньшие дроби:
, значит, исследуемый интеграл тоже сходится.

И ещё раз заметьте, что при таком оформлении решения, мы не озадачиваемся вопросом, выполнено ли это неравенство на всём промежутке интегрирования – важно, что оно выполняется в окрестности точки разрыва, чего вполне достаточно для обоснования факта сходимости.

Вспоминаем с предыдущего занятия, что не знаменателем единым живо исследование:

Пример 10

Исследовать сходимость интеграла

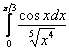
Решение: важным моментом является то, что косинус здесь положителен и убывает от до , таким образом, на промежутке :
, значит, по признаку сравнения, исследуемый интеграл сходится вместе с «эталонным» интегралом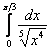

Решаем самостоятельно:

Пример 11

Исследовать сходимость несобственных интегралов 2-го рода

а) 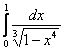– баян, и б) – интеграл позанятнее, для его анализа посмотрИте на график синуса и выполните «прикидку» на калькуляторе.

Решения и ответы в конце урока.

Довольно часто при исследовании несобственных интегралов используют замечательные эквивалентности:

Пример 12

Исследовать сходимость интеграла 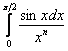при различных значениях .

Решение: ну, во-первых, сразу отметим, что при предложенный интеграл является обычным определённым интегралом, который равен конечному числу, т.е. сходится.

Осталось рассмотреть случай . При «икс», стремящемся к нулю справа имеет место эквивалентность , и поэтому в подынтегральной функции синус можно заменить эквивалентной бесконечно малой, то есть «иксом»:
– если этот момент не понятен, освежаем знания по ссылке выше!

Таким образом, в плане сходимости исследуемый интеграл 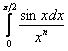ведёт себя точно так же (эквивалентно), как и интеграл , а последний является «эталонным»: при он сходится, а при – расходится.

Любопытно отметить, что на промежутке интеграл тоже является определённым. Но как же так? – ведь тогда эквивалентный ему интеграл, например, 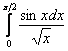вроде бы несобственный. А вот и нет! На самом деле перед нами определённый интеграл с точкой устранимого разрыва («выколотой» точкой) на левом конце. В этом легко убедиться, вычислив соответствующий предел подынтегральной функции, и воспользовавшись первым замечательным пределом:
, то есть, на левом конце промежутка интегрирования подынтегральная функция стремится к нулю, а вовсе не к бесконечности.

Ответ дадим лаконично: исследуемый интеграл сходится при и расходится в остальных случаях.

И, как следует из анализа, при он не является несобственным. Но об этом нас, собственно, никто не спрашивал.

Следующий интеграл запостил на mathprofi.com один из посетителей сайта, и сегодня я с удовольствием разъясню его самой широкой аудитории:

Пример 13

Исследовать сходимость несобственного интеграла

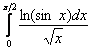
Счастливый номер и интереснейшее решение:

В свете предыдущего исследования, убедимся в том, что подынтегральная функция действительно терпит бесконечный разрыв на левом конце промежутка:
– подробно показал, что неопределённости тут нет, и предел действительно бесконечен. Причём, в пределе получился знак «минус», и это не случайно – на предложенном промежутке интегрирования синус изменяется от 0 до 1, а натуральный логарифм (смотрим или вспоминаем график!) здесь отрицателен.

При справедлива эквивалентность , и поэтому:
, таким образом, интеграл 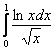эквивалентен исходному интегралу в плане сходимости. Последний интеграл берётся по частям, но есть более быстрый способ исследования.

Во-первых, заметим, что подынтегральная функция неположительна на , однако признак сравнения работает и в нижней полуплоскости (ну а чем она хуже?) – важно, чтобы функции были интегрируемы, и выполнялось неравенство . Тогда из сходимости интеграла «жэ» следует сходимость интеграла «эф», или из расходимости «эф» следует расходимость «жэ».

Но к чему нам лишние неудобства? – просто добавим к логарифму модуль, и картинка отобразится симметрично наверх относительно оси :
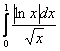, кстати, вместо модуля можно поставить «минус», и это тоже вариант.

А теперь добавьте в свой справочник следующий факт:

При функция более высокого порядка роста, чем . И тут я хочу предостеречь вас от «пижонского» анализа, когда для выяснения порядка роста подставляют конкретное число. Так, если для «прикидки» взять 0,01 и вычислить:
, то легко сделать ошибочный вывод, что при логарифм растёт быстрее. А мораль такова, что если какое-то неравенство имеет место при 0,01, то нет никакой гарантии, что оно останется справедливым при 0,001 или более малом значении «икс». Вот зачем нужна строгая теория и строгие доказательства математического анализа!

Но возвращаемся к задаче. Так как при функция более высокого порядка роста, чем , то:

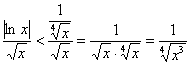– всем понятны эти «школьные» преобразования?

Таким образом, интеграл 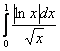сходится вместе с «эталонным» интегралом , следовательно, сходится и «симметричный» интеграл 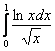. Вместо модуля тут можно было составить неравенство , и тогда, по признаку сравнения, из сходимости интеграла 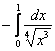следует сходимость 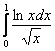. Или же использовать знак «минус», получая эквивалентный интеграл 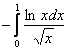с неравенством .

И, в силу установленной выше эквивалентности, исследуемый интеграл 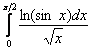сходится вместе с интегралом .

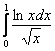Из разобранного примера следует, что интеграл вида 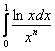сходится и при любом значении . А другой случай для самостоятельного исследования:

Пример 14

а) Исследовать интеграл 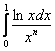на сходимость при . В качестве «опорного» интеграла для сравнения взять интеграл 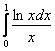, сходимость или расходимость которого установить прямым вычислением. Не забывайте, что графики всех этих подынтегральных функций лежат под осью !

б) Исследовать на сходимость интеграл 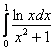– неожиданно, но результат здесь окажется неожиданным.

Если возникли трудности, посмотрите уже, наконец, график логарифма :) Моя версия решения в конце этого «приключенческого» урока! – даже сам не ожидал, что получится так интересно.

И перед тем, как продолжить, ещё раз выделю момент, которой попросил уточнить один из читателей: если дан несобственный интеграл 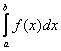, причём на промежутке интегрирования, то можно исследовать эквивалентный интеграл либо 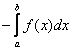. Это обусловлено геометрией преобразования графиков.

Продолжаем:

Как и в случае с интегралами 1-го рода, для интегралов 2-го рода существует аналогичный предельный признак, сформулирую его для разрыва слева:

Пусть неотрицательные подынтегральные функции интегралов 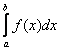(1), 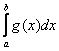(2) непрерывны на и терпят бесконечный разрыв в точке , и пусть существует предел . Тогда:

1) если конечное число, отличное от нуля, то интегралы (1) и (2) сходятся или расходятся одновременно;

2) если , то из сходимости интеграла (2) следует сходимость интеграла (1);

3) если , то из расходимости (2) следует расходимость (1).

На практике обычно используют 1-й пункт признака.

Так, интеграл 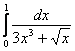Примера 9 легко сравнить со сходящимся интегралом (помним, что ориентироваться нужно на самую маленькую степень «икса»!). Составляем предел, избавляемся от четырёхэтажности дроби и неопределенности «ноль на ноль»:
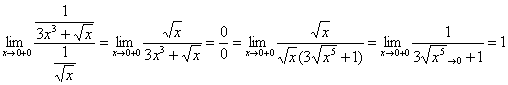– в результате получено конечное число, отличное от нуля, значит, интеграл 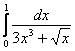сходится вместе с интегралом .

Отношение функций можно составить и наоборот, это даже технически проще:
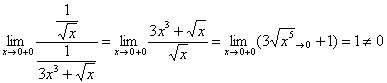– с тем же самым выводом.

Но предельный признак сравнения, конечно, чаще используют в «тяжелых случаях» – когда «обычный» признак применить затруднительно. Ещё один «баян»:

Пример 15

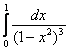
Решение: по «общим очертаниям» данный интеграл должен расходиться, и мы начинаем стандартные рассуждения. На интервале интегрирования:
, следовательно:

и при возведении обеих частей в положительную степень «статус-кво» сохраняется:

Но тогда получается неравенство:
, которое не приносит нам полезной информации. Ведь для обоснования расходимости нужно показать противоположное неравенство!

Что делать? Используя формулу разности квадратов, разложим подынтегральную функцию на множители:
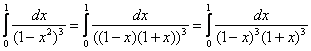, откуда приходит идея сравнить данный интеграл с расходящимся интегралом 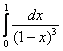с помощью предела:
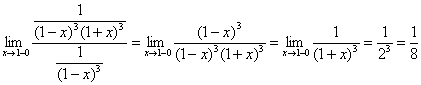– конечное число, отличное от нуля, значит, по предельному признаку сравнения, исследуемый интеграл расходится вместе с интегралом .

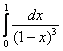Следующие интегралы для самостоятельного решения:

Пример 16

а) исследовать сходимость несобственного интеграла при различных значениях ;

б) исследовать сходимость .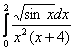

Этими интегралами опять же интересовались посетители сайта, и сейчас я предлагаю вам справиться с ними самостоятельно! Подумайте, как какие функции подобрать для сравнения ;) Краткие решения в конце урока, под занавес которого забьём достойный гвоздь программы:

Пример 17

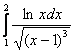
Решение: по «первой оглядке» данный интеграл расходится, но так ли это на самом деле?

Проведём замену переменной: …, да, для несобственных интегралов, точно так же, как и для определённых, работают стандартные приёмы интегрирования – замена, интегрирование по частям и другие! Со своей спецификой. Так, например, интеграл 2-го рода может превратиться в интеграл 1-го рода, и наоборот. Но это не наш случай.

Найдём новые пределы интегрирования. Поскольку , то при новая переменная . Верхний же предел интегрирования: .

И, учитывая, что и , наш интеграл превращается в интеграл:

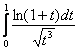
При справедлива эквивалентность , и поэтому в плане сходимости полученный интеграл эквивалентен интегралу:
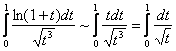, который сходится.

Решение можно оформить академично. Сравним интеграл 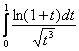со сходящимся интегралом . Используем предельный признак сравнения и соответствующий замечательный предел:
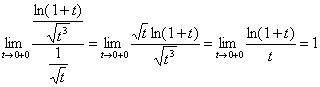– конечное число, отличное от нуля, значит, интеграл 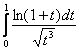сходится, и в силу проведённой замены, исходный интеграл тоже сходится.

Продвинутые читатели могут обойтись без всяких замен:
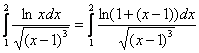и воспользоваться эквивалентностью при , но такую возможность нужно ещё увидеть.

И в заключение урока ответим на следующий важный вопрос: что делать, если подынтегральная функция терпит бесконечный разрыв на обоих концах отрезка? Например:

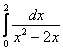
Всё очень просто – используя свойство аддитивности, делим интеграл на 2 части:

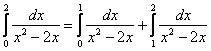
Если сходятся обе части, то сходиться будет и весь интеграл; если хотя бы одна из частей расходится, то аминь.

Если вдруг точек разрыва больше – делим интеграл на бОльшее количество частей.

То же самое касается интегралов-«ассорти», например, 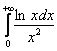. Делим его на 2 части, напрашивается так:
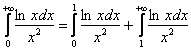, и если сходятся обе части, то сходиться будет и весь интеграл

Кстати, как мы выяснили в Примере 14, интеграл 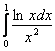расходится, и поэтому надобность исследования интеграла отпадает.

Для фанатов есть дополнительный материал – это то, что мне больше всего приглянулось в Сети.

Жду вас в заключительной части урока – Абсолютная и условная сходимость несобственных интегралов.

Решения и ответы:

Пример 8. Решение: вычислим несобственные интегралы:
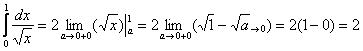– конечное число, т.е. данный интеграл сходится;
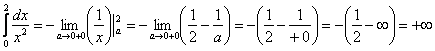, т.е. интеграл расходится.

а) Исследуем сходимость интеграла . Сравним данный интеграл со сходящимся интегралом . На промежутке :
, следовательно:
, значит, по признаку сравнения исследуемый интеграл сходится вместе с интегралом .

б) Сравним интеграл с интегралом с расходящимся интегралом . Так как желаемое неравенство выполнено не на всём промежутке интегрирования, то решение удобно оформить другим способом. При :
, поэтому:
, значит, по признаку сравнения, исследуемый интеграл расходится.

Пример 11. Решение:

а) на промежутке :
, поэтому:
(хорошо осмыслите, почему так!)
При возведении обеих частей в положительную степень (в данном случае в 1/3) знак неравенства сохраняется:
, а бОльшим знаменателям соответствуют мЕньшие дроби:
, значит, по признаку сравнения, исследуемый интеграл сходится вместе с интегралом 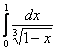(«эталонный» интеграл).

б) На промежутке интегрирования синус принимает минимальное значение в точке . Поэтому на данном промежутке:
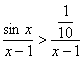, таким образом, исследуемый интеграл расходится вместе с интегралом (множитель-константа не влияет на сходимость или расходимость).

Пример 14. Решение:

а) Вычислим интеграл:
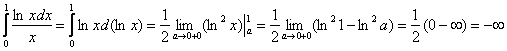, т.е. несобственный интеграл расходится.
Для любого из полуинтервала и для любого справедливо неравенство:
, следовательно:

Логарифм на данном промежутке отрицателен (кроме точки ), поэтому при домножении на него обеих частей, у неравенства следует сменить знак:
, значит, по признаку сравнения, интеграл 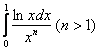расходится вместе с интегралом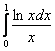
Геометрическое пояснение: графики функций лежат ниже графика , и бесконечная площадь 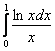является частью бОльшей площади .

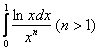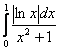б) Рассмотрим симметричную относительно оси функцию и интеграл . При функция более высокого порядка роста, чем , поэтому:

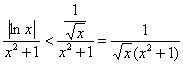
на промежутке справедливо неравенство , следовательно:
– и по построенной цепочке неравенств, по признаку сравнения, интеграл 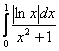сходится вместе с интегралом .

Таким образом, в силу симметрии графиков подынтегральных функций относительно оси абсцисс, сходится и интеграл .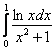

Пример 16. Решение:

а) Сравним предложенный интеграл с интегралом . Используем предельный признак сравнения:
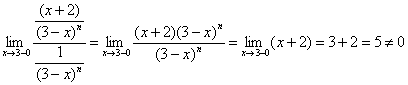– конечное число, значит, исследуемый интеграл сходится или расходится вместе с интегралом , а последний сходится при и расходится при .

б) При справедлива эквивалентность , поэтому в плане сходимости исследуемый интеграл эквивалентен интегралу:

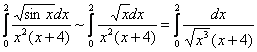
Сравним последний интеграл с расходящимся интегралом . Используем предельный признак сравнения:
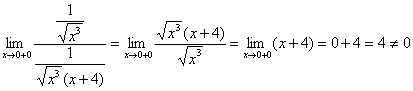– конечное число, значит, интеграл 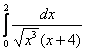расходится вместе с интегралом , и в силу установленной эквивалентности, расходится и исследуемый интеграл.

Второй способ: сразу сравнить «пациента» с «эталонным» интегралом и воспользоваться первым замечательным пределом:

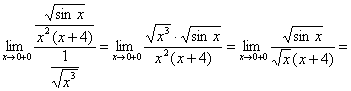
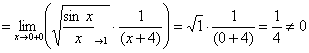– с тем же финальным выводом.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?