


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Нормальный закон распределения вероятностей
Без преувеличения его можно назвать философским законом. Наблюдая за различными объектами и процессами окружающего мира, мы часто сталкиваемся с тем, что чего-то бывает мало, и что бывает норма:
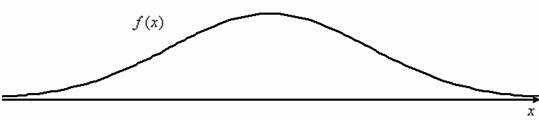
Перед вами принципиальный вид функции плотности нормального распределения вероятностей, и я приветствую вас на этом интереснейшем уроке.
Какие можно привести примеры? Их просто тьма. Это, например, рост, вес людей (и не только), их физическая сила, умственные способности и т. д. Существует «основная масса» (по тому или иному признаку) и существуют отклонения в обе стороны.
Это различные характеристики неодушевленных объектов (те же размеры, вес). Это случайная продолжительность процессов, например, время забега стометровки или превращения смолы в янтарь. Из физики вспомнились молекулы воздуха: среди них есть медленные, есть быстрые, но большинство двигаются со «стандартными» скоростями.
Более того, даже дискретные распределения бывают близкИ к нормальному, и в конце урока мы раскроем важный секрет «нормальности».
В чём вероятностный смысл нормального распределения? …Ещё раз взглянИте на график («колокол») выше…. Смысл состоит в том, что если мы наугад выберем объект из нормально распределённой совокупности (например, человека), то с большой вероятностью он окажется «среднестатистическим» (по тому или иному показателю). Именно поэтому так трудно встретить какого-то «особенного» человека…. Ну а сейчас математика, математика, математика, которая в древности не зря считалась философией!
Начинающим рекомендую изучать всё по порядку, и самоварам – оглавление:
- Функция плотности нормального распределения, формула, параметры.
- Как построить график плотности нормального распределения? Видео прилагается.
- Функция распределения нормального распределения, и попутно мы решаем, конечно, везде задачи.
- Вероятность попадания в интервал (того, что нормальная СВ примет значение из заданного интервала).
- Правило «трёх сигм».
- Понятие о центральной предельной теореме (теореме Ляпунова).
Приступаем.
Непрерывная случайная величина ![]() , распределённая по нормальному закону, имеет функцию плотности
, распределённая по нормальному закону, имеет функцию плотности 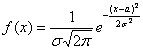 (не пугаемся) и однозначно определяется параметрами
(не пугаемся) и однозначно определяется параметрами ![]() и
и ![]() .
.
Данная функция получила фамилию некоронованного короля математики, и я не могу удержаться, чтобы не запостить:

Одну из таких купюр мне довелось лично держать в руках, и ещё будучи школьником я внимательно изучил функцию Гаусса, правда, ничего не понял :) Педантичные немцы отобразили все её особенности (на картинке видно плохо), и мы с толком, с расстановкой приступаем к их немцев изучению.
Начнём с того, что для функции 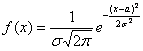 выполнены свойства плотности вероятностей , а именно
выполнены свойства плотности вероятностей , а именно ![]() (почему?) и
(почему?) и 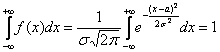 , откуда следует, что нормально распределённая случайная величина достоверно примет одно из действительных значений. Теоретически – какое угодно, практически – узнаем позже.
, откуда следует, что нормально распределённая случайная величина достоверно примет одно из действительных значений. Теоретически – какое угодно, практически – узнаем позже.
Любопытно отметить, что сам по себе неопределённый интеграл ![]() является неберущимся, однако указанный выше несобственный интеграл сходится и равен
является неберущимся, однако указанный выше несобственный интеграл сходится и равен 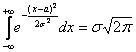 . Вычисления для простейшего случая
. Вычисления для простейшего случая ![]() можно найти здесь, все же остальные варианты сводятся к нему с помощью линейной замены
можно найти здесь, все же остальные варианты сводятся к нему с помощью линейной замены ![]() .
.
Следующие замечательные факты я тоже приведу без доказательства:
![]() – то есть математическое ожидание нормально распределённой случайной величины в точности равно «а», а среднее квадратическое отклонение в точности равно «сигме»:
– то есть математическое ожидание нормально распределённой случайной величины в точности равно «а», а среднее квадратическое отклонение в точности равно «сигме»: ![]() .
.
Эти значения выводятся с помощью общих формул математического ожидания и дисперсии, и желающие / нуждающиеся могут ознакомиться с подробными выкладками в учебной литературе, и совсем здОрово, если вам удастся провести их самостоятельно.
Ну а мы переходим к насущным практическим вопросам. Практики сегодня будет много, и она будет интересна не только «чайникам», но и более подготовленным читателям:
Пример 1
Нормально распределённая случайная величина задана параметрами ![]() . Записать её функцию плотности и построить график.
. Записать её функцию плотности и построить график.
Несмотря на кажущуюся простоту задания, в нём существует немало тонкостей.
Первый момент касается обозначений. Они стандартные, и никаких вольностей: математическое ожидание обозначают буквой ![]() (реже
(реже ![]() или
или ![]() («мю»)), а стандартное отклонение – буквой
(«мю»)), а стандартное отклонение – буквой ![]() . Кстати, обратите внимание на формулировку: в условии ничего не сказано о сущности параметров «а» и «сигма», и несведущий человек может только догадываться, что это такое.
. Кстати, обратите внимание на формулировку: в условии ничего не сказано о сущности параметров «а» и «сигма», и несведущий человек может только догадываться, что это такое.
Решение начнём шаблонной фразой: функция плотности нормально распределённой случайной величины имеет вид 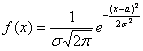 . В данном случае
. В данном случае ![]() и:
и:
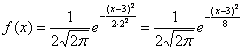
Первая, более лёгкая часть задачи выполнена. Теперь график. Вот на нём-то, на моей памяти, студентов «заворачивали» десятки раз, причём, многих неоднократно. По той причине, что график ![]() обладает несколькими принципиальными особенностями, которые нужно обязательно отобразить на чертеже.
обладает несколькими принципиальными особенностями, которые нужно обязательно отобразить на чертеже.
Сначала полная картина, затем комментарии:
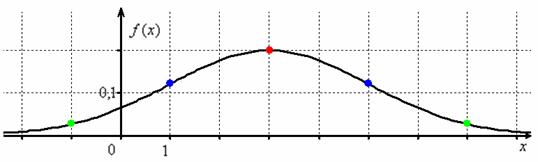
Строим декартову систему координат. При выполнении чертежа от руки во многих случаях оптимален следующий масштаб:
по оси абсцисс: 2 тетрадные клетки = 1 ед.;
по оси ординат: 2 тетрадные клетки = 0,1 ед., при этом саму ось следует расположить из тех соображений, что в точке ![]() функция достигает максимума, и вертикальная прямая
функция достигает максимума, и вертикальная прямая ![]() (на чертеже отсутствует) является линией симметрии графика.
(на чертеже отсутствует) является линией симметрии графика.
И логично, что в первую очередь удобно найти максимум функции. В данном примере он находится в точке ![]() :
:
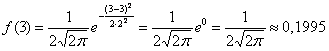
Отмечаем вершину графика (красная точка).
Далее вычислим значения функции при ![]() , а точнее только одно из них – в силу симметрии графика они равны:
, а точнее только одно из них – в силу симметрии графика они равны:

Отмечаем синим цветом.
Внимание! ![]() – это точки перегиба нормальной кривой. На интервале
– это точки перегиба нормальной кривой. На интервале ![]() график является выпуклым, а на крайних интервалах – вогнутым.
график является выпуклым, а на крайних интервалах – вогнутым.
Далее отклоняемся от центра ещё на одно стандартное отклонение ![]() и рассчитываем высоту:
и рассчитываем высоту:

Отмечаем точки на чертеже (зелёный цвет) и видим, что этого вполне достаточно.
На завершающем этапе аккуратно чертим график, и особо аккуратно отражаем его выпуклость / вогнутость! Ну и, наверное, вы давно поняли, что ось абсцисс – это горизонтальная асимптота, и «залезать» за неё категорически нельзя!
При электронном оформлении решения график легко построить в Экселе, и неожиданно для самого себя я даже записал короткий видеоролик на эту тему. Но сначала поговорим о том, как меняется форма нормальной кривой в зависимости от значений ![]() и
и ![]() .
.
При увеличении или уменьшении «а» (при неизменном «сигма») график сохраняет свою форму и перемещается вправо / влево соответственно. Так, например, при ![]() функция принимает вид
функция принимает вид ![]() и наш график «переезжает» на 3 единицы влево – ровнехонько в начало координат:
и наш график «переезжает» на 3 единицы влево – ровнехонько в начало координат:
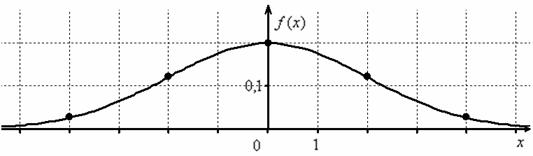
Нормально распределённая величина с нулевым математическим ожиданием получила вполне естественное название – центрированная; её функция плотности 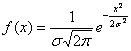 – чётная, и график симметричен относительно оси ординат.
– чётная, и график симметричен относительно оси ординат.
В случае изменения «сигмы» (при постоянном «а»), график «остаётся на месте», но меняет форму. При увеличении ![]() он становится более низким и вытянутым, словно осьминог, растягивающий щупальца. И, наоборот, при уменьшении
он становится более низким и вытянутым, словно осьминог, растягивающий щупальца. И, наоборот, при уменьшении ![]() график становится более узким и высоким – получается «удивлённый осьминог». Так, при уменьшении «сигмы» в два раза:
график становится более узким и высоким – получается «удивлённый осьминог». Так, при уменьшении «сигмы» в два раза: ![]() предыдущий график сужается и вытягивается вверх в два раза:
предыдущий график сужается и вытягивается вверх в два раза:
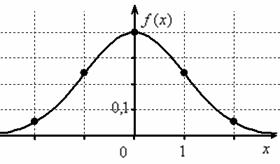
Всё в полном соответствии с геометрическими преобразованиями графиков.
Нормальное распределёние с единичным значением «сигма» называется нормированным, а если оно ещё и центрировано (наш случай), то такое распределение называют стандартным. Оно имеет ещё более простую функцию плотности, которая уже встречалась в локальной теореме Лапласа: ![]() . Стандартное распределение нашло широкое применение на практике, и очень скоро мы окончательно поймём его предназначение.
. Стандартное распределение нашло широкое применение на практике, и очень скоро мы окончательно поймём его предназначение.
Ну а теперь смотрим кино, на Ютубе – ниже, на Рутубе – тут.
Да, совершенно верно – как-то незаслуженно у нас осталась в тени функция распределения вероятностей. Вспоминаем её определение:
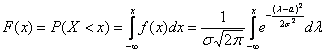 – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение, МЕНЬШЕЕ, чем переменная
примет значение, МЕНЬШЕЕ, чем переменная ![]() , которая «пробегает» все действительные значения до «плюс» бесконечности.
, которая «пробегает» все действительные значения до «плюс» бесконечности.
Внутри интеграла обычно используют другую букву, чтобы не возникало «накладок» с обозначениями, ибо здесь каждому значению ![]() ставится в соответствие несобственный интеграл
ставится в соответствие несобственный интеграл 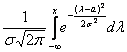 , который равен некоторому числу из интервала
, который равен некоторому числу из интервала ![]() .
.
Почти все значения ![]() не поддаются точному расчету, но нам этого и не нужно, с современным ПО их можно вычислить быстро и с очень высокой точностью.Так, для функции
не поддаются точному расчету, но нам этого и не нужно, с современным ПО их можно вычислить быстро и с очень высокой точностью.Так, для функции 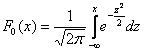 стандартного распределения
стандартного распределения ![]() соответствующая экселевская функция вообще содержит один аргумент:
соответствующая экселевская функция вообще содержит один аргумент:
=НОРМСТРАСП(z)
Раз, два – и готово:
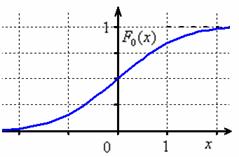
На чертеже хорошо видно выполнение всех свойств функции распределения, и из технических нюансов здесь следует обратить внимание на горизонтальные асимптоты и точку перегиба ![]() .
.
Теперь вспомним одну из ключевых задач темы, а именно выясним, как найти ![]() – вероятность того, что нормальная случайная величина
– вероятность того, что нормальная случайная величина ![]() примет значение из интервала
примет значение из интервала ![]() . Геометрически эта вероятность равна площади между нормальной кривой и осью абсцисс на соответствующем участке:
. Геометрически эта вероятность равна площади между нормальной кривой и осью абсцисс на соответствующем участке:
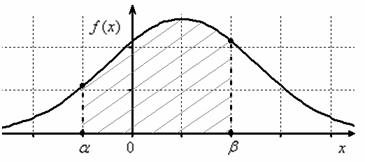
но каждый раз вымучивать приближенное значение  неразумно, и поэтому здесь рациональнее использовать «лёгкую» формулу:
неразумно, и поэтому здесь рациональнее использовать «лёгкую» формулу:
![]() .
.
! Вспоминаем также, что ![]()
Тут можно снова задействовать Эксель, но есть пара весомых «но»: во-первых, он не всегда под рукой, а во-вторых, «готовые» значения ![]() , скорее всего, вызовут вопросы у преподавателя. Почему?
, скорее всего, вызовут вопросы у преподавателя. Почему?
Об этом я неоднократно рассказывал ранее: в своё время (и ещё не очень давно) роскошью был обычный калькулятор, и в учебной литературе до сих пор сохранился «ручной» способ решения рассматриваемой задачи. Его суть состоит в том, чтобы стандартизировать значения «альфа» и «бета», то есть свести решение к стандартному распределению:
![]()
Примечание: функцию ![]() легко получить из общего случая
легко получить из общего случая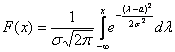 с помощью линейной замены
с помощью линейной замены ![]() . Тогда
. Тогда ![]() и:
и:
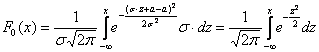
и из проведённой замены как раз следует формула ![]() перехода от значений
перехода от значений ![]() произвольного распределения – к соответствующим значениям
произвольного распределения – к соответствующим значениям ![]() стандартного распределения.
стандартного распределения.
Зачем это нужно? Дело в том, что значения ![]() скрупулезно подсчитаны нашими предками и сведены в специальную таблицу, которая есть во многих книгах по терверу. Но ещё чаще встречается таблица значений
скрупулезно подсчитаны нашими предками и сведены в специальную таблицу, которая есть во многих книгах по терверу. Но ещё чаще встречается таблица значений ![]() , с которой мы уже имели дело в интегральной теореме Лапласа:
, с которой мы уже имели дело в интегральной теореме Лапласа:
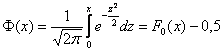
В силу очевидной нечётности функции Лапласа (![]() ), в таблице представлены её значения только для положительных «икс», и по причине симметрии нормального распределения этого оказывается достаточно. Итак, вероятность того, что нормальная случайная величина
), в таблице представлены её значения только для положительных «икс», и по причине симметрии нормального распределения этого оказывается достаточно. Итак, вероятность того, что нормальная случайная величина ![]() с параметрами
с параметрами ![]() и
и ![]() примет значение из интервала
примет значение из интервала ![]() , можно вычислить по формуле:
, можно вычислить по формуле:
![]() , где
, где ![]() – функция Лапласа.
– функция Лапласа.
Таким образом, наша задача становится чуть ли не устной! Порой, здесь хмыкают и говорят, что метод устарел. Может быть…, но парадокс состоит в том, что «устаревший метод» очень быстро приводит к результату! И ещё в этом заключена большая мудрость – если вдруг пропадёт электричество или восстанут машины, то у человечества останется возможность заглянуть в бумажные таблицы и спасти мир =)
Пример 2
Из пункта ![]() ведётся стрельба из орудия вдоль прямой
ведётся стрельба из орудия вдоль прямой ![]() . Предполагается, что дальность полёта распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в процентах) сколько снарядов упадёт с перелётом от 5 до 70м.
. Предполагается, что дальность полёта распределена нормально с математическим ожиданием 1000 м и средним квадратическим отклонением 5 м. Определить (в процентах) сколько снарядов упадёт с перелётом от 5 до 70м.
Классика жанра.
Решение: в задаче рассматривается нормально распределённая случайная величина ![]() – дальность полёта снаряда, и по условию
– дальность полёта снаряда, и по условию ![]() .
.
Так как речь идёт о перелёте за цель, то ![]() . Вычислим вероятность
. Вычислим вероятность ![]() – того, что снаряд упадёт в пределах этой дистанции.
– того, что снаряд упадёт в пределах этой дистанции.
Если в нашем распоряжении есть таблица значений функции 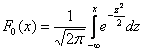 , то используем формулу
, то используем формулу ![]() :
:
![]()
Для самопроверки можно задействовать экселевскую функцию =НОРМСТРАСП(z) или напрямую «забить» ![]() и затем
и затем ![]() в Пункт 9 расчётного макета.
в Пункт 9 расчётного макета.
Если же в нашем распоряжении есть таблица значений функции Лапласа 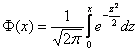 , то решаем через неё:
, то решаем через неё:
![]()
Дробные значения традиционно округляем до 4 знаков после запятой, как это сделано в типовой таблице. И для контроля есть Пункт 5 макета.
Напоминаю, что ![]() , и во избежание путаницы всегда контролируйте, таблица КАКОЙ функции перед вашими глазами.
, и во избежание путаницы всегда контролируйте, таблица КАКОЙ функции перед вашими глазами.
Ответ требуется дать в процентах, поэтому рассчитанную вероятность нужно умножить на 100 и снабдить результат содержательным комментарием:
– с перелётом от 5 до 70 м упадёт примерно 15,87% снарядов
Тренируемся самостоятельно:
Пример 3
Диаметр подшипников, изготовленных на заводе, представляет собой случайную величину, распределенную нормально с математическим ожиданием 1,5 см и средним квадратическим отклонением 0,04 см. Найти вероятность того, что размер наугад взятого подшипника колеблется от 1,4 до 1,6 см.
В образце решения и далее я буду использовать функцию Лапласа, как самый распространённый вариант. Кстати, обратите внимание, что согласно формулировке, здесь можно включить концы интервала в рассмотрение. Впрочем, это не критично.
И уже в этом примере нам встретился особый случай – когда интервал ![]() симметричен относительно математического ожидания. В такой ситуации его можно записать в виде
симметричен относительно математического ожидания. В такой ситуации его можно записать в виде ![]() и, пользуясь нечётностью функции Лапласа, упростить рабочую формулу:
и, пользуясь нечётностью функции Лапласа, упростить рабочую формулу:
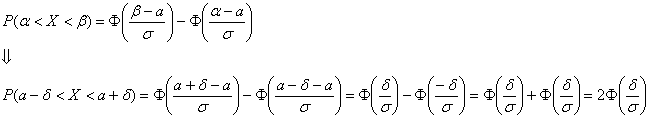
Параметр «дельта» называют отклонением от математического ожидания, и двойное неравенство можно «упаковывать» с помощью модуля:
![]() – вероятность того, что значение случайной величины
– вероятность того, что значение случайной величины ![]() отклонится от математического ожидания менее чем на
отклонится от математического ожидания менее чем на ![]() .
.
Хорошо то решение, которое умещается в одну строчку:)
![]() – вероятность того, что диаметр наугад взятого подшипника отличается от 1,5 см не более чем на 0,1 см.
– вероятность того, что диаметр наугад взятого подшипника отличается от 1,5 см не более чем на 0,1 см.
Результат этой задачи получился близким к единице, но хотелось бы ещё бОльшей надежности – а именно, узнать границы, в которых находится диаметр почти всех подшипников. Существует ли какой-нибудь критерий на этот счёт? Существует! На поставленный вопрос отвечает так называемое
правило «трех сигм»
Его суть состоит в том, что практически достоверным является тот факт, что нормально распределённая случайная величина ![]() примет значение из промежутка
примет значение из промежутка ![]() .
.
И в самом деле, вероятность отклонения от матожидания менее чем на ![]() составляет:
составляет:
![]() или 99,73%
или 99,73%
В «пересчёте на подшипники» – это 9973 штуки с диаметром от 1,38 до 1,62 см и всего лишь 27 «некондиционных» экземпляров.
В практических исследованиях правило «трёх сигм» обычно применяют в обратном направлении: если статистически установлено, что почти все значения исследуемой случайной величины укладываются в интервал длиной 6 стандартных отклонений, то появляются веские основания полагать, что эта величина распределена по нормальному закону. Проверка осуществляется с помощью теории статистических гипотез.
Продолжаем решать суровые советские задачи:
Пример 4
Случайная величина ![]() ошибки взвешивания распределена по нормальному закону с нулевым математическим ожиданием и стандартным отклонением 3 грамма. Найти вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей по модулю 5 грамм.
ошибки взвешивания распределена по нормальному закону с нулевым математическим ожиданием и стандартным отклонением 3 грамма. Найти вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей по модулю 5 грамм.
Решение очень простое. По условию, ![]() и сразу заметим, что при очередном взвешивании (чего-то или кого-то) мы почти 100% получим результат с точностью до 9 грамм. Но в задаче фигурирует более узкое отклонение
и сразу заметим, что при очередном взвешивании (чего-то или кого-то) мы почти 100% получим результат с точностью до 9 грамм. Но в задаче фигурирует более узкое отклонение ![]() и по формуле
и по формуле ![]() :
:
![]() – вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей 5 грамм.
– вероятность того, что очередное взвешивание будет проведено с ошибкой, не превышающей 5 грамм.
Ответ: ![]()
Прорешанная задача принципиально отличается от вроде бы похожего Примера 3 урока о равномерном распределении. Там была погрешность округления результатов измерений, здесь же речь идёт о случайной погрешности самих измерений. Такие погрешности возникают в связи с техническими характеристиками самого прибора (диапазон допустимых ошибок, как правило, указывают в его паспорте), а также по вине экспериментатора – когда мы, например, «на глазок» снимаем показания со стрелки тех же весов.
Помимо прочих, существуют ещё так называемые систематические ошибки измерения. Это уже неслучайные ошибки, которые возникают по причине некорректной настройки или эксплуатации прибора. Так, например, неотрегулированные напольные весы могут стабильно «прибавлять» килограмм, а продавец систематически обвешивать покупателей. Или не систематически ведь можно обсчитать. Однако, в любом случае, случайной такая ошибка не будет, и её матожидание отлично от нуля.
…Срочно разрабатываю курс по подготовке продавцов =)
Самостоятельно решаем обратную задачу:
Пример 5
Диаметр валика – нормально распределенная случайная величина, среднее квадратическое отклонение ее равно ![]() мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью
мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью ![]() попадет длина диаметра валика.
попадет длина диаметра валика.
Пункт 5* расчётного макета в помощь. Обратите внимание, что здесь не известно математическое ожидание, но это нисколько не мешает решить поставленную задачу.
И экзаменационное задание, которое я настоятельно рекомендую для закрепления материала:
Пример 6
Нормально распределенная случайная величина ![]() задана своими параметрами
задана своими параметрами ![]() (математическое ожидание) и
(математическое ожидание) и ![]() (среднее квадратическое отклонение). Требуется:
(среднее квадратическое отклонение). Требуется:
а) записать плотность вероятности и схематически изобразить ее график;
б) найти вероятность того, что ![]() примет значение из интервала
примет значение из интервала ![]() ;
;
в) найти вероятность того, что ![]() отклонится по модулю от
отклонится по модулю от ![]() не более чем на
не более чем на ![]() ;
;
г) применяя правило «трех сигм», найти значения случайной величины ![]() .
.
Такие задачи предлагаются повсеместно, и за годы практики мне их довелось решить сотни и сотни штук. Обязательно попрактикуйтесь в ручном построении чертежа и использовании бумажных таблиц ;)
Ну а я разберу пример повышенной сложности:
Пример 7
Плотность распределения вероятностей случайной величины ![]() имеет вид
имеет вид ![]() . Найти
. Найти ![]() , математическое ожидание
, математическое ожидание ![]() , дисперсию
, дисперсию ![]() , функцию распределения
, функцию распределения ![]() , построить графики плотности и функции распределения, найти
, построить графики плотности и функции распределения, найти ![]() .
.
Решение: прежде всего, обратим внимание, что в условии ничего не сказано о характере случайной величины. Само по себе присутствие экспоненты ещё ничего не значит: это может оказаться, например, показательное или вообще произвольное непрерывное распределение. И поэтому «нормальность» распределения ещё нужно обосновать:
Так как функция ![]() определена при любом действительном значении
определена при любом действительном значении ![]() , и её можно привести к виду
, и её можно привести к виду 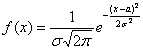 , то случайная величина
, то случайная величина ![]() распределена по нормальному закону.
распределена по нормальному закону.
Приводим. Для этого выделяем полный квадрат и организуем трёхэтажную дробь:
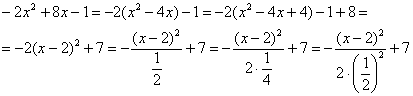
Обязательно выполняем проверку, возвращая показатель в исходный вид:
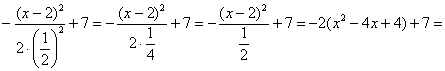
![]() , что мы и хотели увидеть.
, что мы и хотели увидеть.
Таким образом:
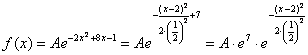 – по правилу действий со степенями «отщипываем»
– по правилу действий со степенями «отщипываем» ![]() . И здесь можно сразу записать очевидные числовые характеристики:
. И здесь можно сразу записать очевидные числовые характеристики:
![]()
Теперь найдём значение параметра ![]() . Поскольку множитель нормального распределения имеет вид
. Поскольку множитель нормального распределения имеет вид ![]() и
и ![]() , то:
, то:
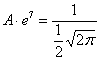 , откуда выражаем
, откуда выражаем ![]() и подставляем в нашу функцию:
и подставляем в нашу функцию:
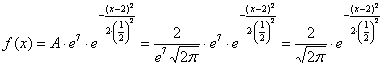 , после чего ещё раз пробежимся по записи глазами и убедимся, что полученная функция имеет вид
, после чего ещё раз пробежимся по записи глазами и убедимся, что полученная функция имеет вид 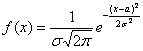 .
.
Построим график плотности:
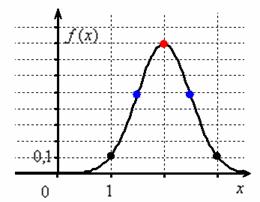
и график функции распределения 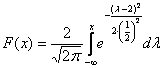 :
:
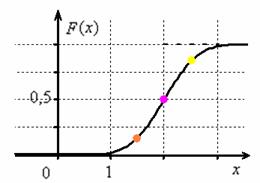
Если под рукой нет Экселя и даже обычного калькулятора, то последний график легко строится вручную! В точке ![]() функция распределения принимает значение
функция распределения принимает значение ![]() и здесь находится перегиб графика (малиновая точка) Кроме того, для более или менее приличного чертежа желательно найти ещё хотя бы пару точек. Берём традиционное значение
и здесь находится перегиб графика (малиновая точка) Кроме того, для более или менее приличного чертежа желательно найти ещё хотя бы пару точек. Берём традиционное значение ![]() и стандартизируем его по формуле
и стандартизируем его по формуле ![]() . Далее с помощью таблицы значений функции Лапласа находим:
. Далее с помощью таблицы значений функции Лапласа находим: ![]() – жёлтая точка на чертеже. С симметричной оранжевой точкой никаких проблем:
– жёлтая точка на чертеже. С симметричной оранжевой точкой никаких проблем: ![]() и:
и:
![]() .
.
После чего аккуратно проводим интегральную кривую, не забывая о перегибе и двух горизонтальных асимптотах.
Да, и ещё нужно вычислить:
![]() – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение из данного отрезка.
примет значение из данного отрезка.
Ответ: 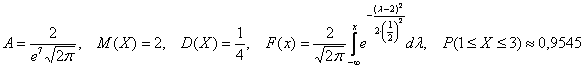
Но этим, конечно, всё дело не ограничивается! Дополнительные примеры, причём довольно творческие, можно найти в тематической pdf-книжке.
И в заключение урока обещанный секрет:
понятие о центральной предельной теореме
которую также называют теоремой Ляпунова. Её суть состоит в том, что если случайная величина ![]() является суммой очень большого числа взаимно независимых случайных величин
является суммой очень большого числа взаимно независимых случайных величин ![]() , влияние каждой из которых на всю сумму ничтожно мало, то
, влияние каждой из которых на всю сумму ничтожно мало, то ![]() имеет распределение, близкое к нормальному.
имеет распределение, близкое к нормальному.
В окружающем мире условие теоремы Ляпунова выполняется очень часто, и поэтому нормальное распределение (близкое к нему) и встречается буквально на каждом шагу.
Так, например, молекул воздуха очень и очень много, и каждая из них своим движением оказывает ничтожно малое влияние на всю совокупность. Поэтому скорость молекул воздуха распределена нормально.
Большая популяция некоторых особей. Каждая из них (или подавляющее большинство) оказывает несущественное влияние на жизнь всей популяции, следовательно, длина их лапок тоже распределена по нормальному закону.
Теперь вернёмся к знакомой задаче, где проводится ![]() независимых испытаний, в каждом из которых некое событие
независимых испытаний, в каждом из которых некое событие ![]() может появиться с постоянной вероятностью
может появиться с постоянной вероятностью ![]() . Эти испытания можно считать попарно независимым случайными величинами
. Эти испытания можно считать попарно независимым случайными величинами ![]() , и при достаточно большом значении «эн» биномиальное распределение случайной величины
, и при достаточно большом значении «эн» биномиальное распределение случайной величины ![]() – числа появлений события
– числа появлений события ![]() в
в ![]() испытаниях – очень близко к нормальному.
испытаниях – очень близко к нормальному.
Уже при ![]() и
и ![]() в многоугольнике биномиального распределения хорошо просматривается нормальная кривая:
в многоугольнике биномиального распределения хорошо просматривается нормальная кривая:
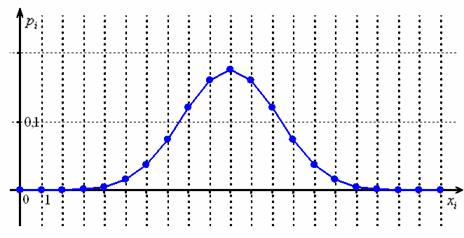
И чем больше ![]() , тем ближе будет сходство. Вероятность
, тем ближе будет сходство. Вероятность ![]() может быть и другой, но не слишком малой.
может быть и другой, но не слишком малой.
Именно этот факт мы и использовали в теоремах Лапласа – когда приближали биномиальные вероятности соответствующими значениями функций нормального распределения.
Вот такие вот пироги.
Необычайно интересной, и я бы даже сказал «сочной» получилась эта статья, что бывает далеко не всегда, но всегда вдохновляет на новое творчество! Надеюсь, вам тоже понравилось, и вы освоили весь материал «на одном дыхании».
До скорых встреч!
Решения и ответы:
Пример 3. Решение: т. к. случайная величина ![]() (диаметр подшипника) распределена нормально, то используем формулу
(диаметр подшипника) распределена нормально, то используем формулу ![]() , где
, где ![]() – функция Лапласа. В данном случае:
– функция Лапласа. В данном случае:
![]()
![]() – вероятность того, что диаметр наугад взятого подшипника будет находиться в пределах от 1,4 до 1,6 см.
– вероятность того, что диаметр наугад взятого подшипника будет находиться в пределах от 1,4 до 1,6 см.
Ответ: ![]()
Пример 5. Решение: используем формулу: ![]() .
.
В данной задаче ![]() , таким образом:
, таким образом:
![]()
![]()
откуда находим:
![]()
Длина искомого интервала составляет ![]()
Ответ: 20 мм
Пример 6. Решение: функция плотности нормально распределённой случайной величины имеет вид 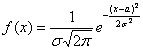 , где
, где ![]() – математическое ожидание,
– математическое ожидание, ![]() – стандартное отклонение. В данном случае
– стандартное отклонение. В данном случае ![]() , следовательно:
, следовательно:
Выполним чертёж:
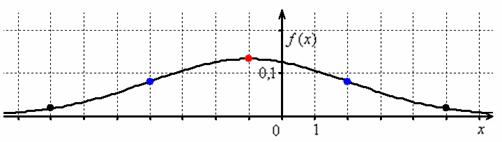
! Примечание: несмотря на то, что условие допускает схематическое построение графика, на чертеже обязательно отображаем все его принципиальные особенности, в частности, на забываем о перегибах в точках ![]() .
.
б) Используем формулу ![]() , где
, где ![]() – функция Лапласа.
– функция Лапласа.
В данной задаче ![]() :
:
![]()
![]() – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение из данного интервала.
примет значение из данного интервала.
в) Используем формулу ![]() для
для ![]() :
:
![]() – вероятность того, что значение случайной величины
– вероятность того, что значение случайной величины ![]() отклонится от её математического ожидания не более чем на 2.
отклонится от её математического ожидания не более чем на 2.
г) Согласно правилу «трех сигм», практически все значения (99,73%) нормально распределенной случайной величины входят в интервал ![]() . В данном случае:
. В данном случае:
![]()
![]() – искомый интервал.
– искомый интервал.
Ответ: а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright