Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Неопределенный интеграл.
Подробные примеры решений

На данном уроке мы начнём изучение темы Неопределенный интеграл, а также подробно разберем примеры решений простейших (и не совсем) интегралов. В этой статье я ограничусь минимумом теории, и сейчас наша задача – научиться решать интегралы.

Что нужно знать для успешного освоения материала? Для того чтобы справиться с интегральным исчислением  Вам необходимо уметь находить производные, минимум, на среднем уровне. Поэтому, если материал запущен, то рекомендую сначала внимательно ознакомиться с уроками Как найти производную? и Производная сложной функции. Не лишним опытом будет, если у Вас за плечами несколько десятков (лучше – сотня) самостоятельно найденных производных. По-крайне мере, Вас не должны ставить в тупик задания на дифференцирование простейших и наиболее распространенных функций. Казалось бы, при чем здесь вообще производные, если речь в статье пойдет об интегралах?! А дело вот в чем. Дело в том, что нахождение производных и нахождение неопределенных интегралов (дифференцирование и интегрирование) – это два взаимно обратных действия, как, например, сложение/вычитание или умножение/деление. Таким образом, без навыка (+ какого-никакого опыта) нахождения производных, к сожалению, дальше не продвинуться.

В этой связи нам потребуются следующие методические материалы: Таблица производных и Таблица интегралов. Справочные пособия можно открыть, закачать или распечатать на странице Математические формулы и таблицы.

В чем сложность изучения неопределенных интегралов? Если в производных имеют место строго 5 правил дифференцирования, таблица производных и довольно четкий алгоритм действий, то в интегралах всё иначе. Существуют десятки способов и приемов интегрирования. И, если способ интегрирования изначально подобран неверно (т.е. Вы не знаете, как решать), то интеграл можно «колоть» буквально сутками, как самый настоящий ребус, пытаясь приметить различные приемы и ухищрения. Некоторым даже нравится. Между прочим, это не шутка, мне довольно часто приходилось слышать от студентов мнение вроде «У меня никогда не было интереса решить предел или производную, но вот интегралы – совсем другое дело, это увлекательно, всегда есть желание «взломать» сложный интеграл». Стоп. Хватит чёрного юмора, переходим к этим самым неопределенным интегралам.

Коль скоро способов решения существует очень много, то с чего же начать изучение неопределенных интегралов чайнику? В интегральном исчислении существуют, на мой взгляд, три столпа или своеобразная «ось», вокруг которой вращается всё остальное. В первую очередь следует хорошо разобраться в простейших интегралах (эта статья). Потом нужно детально проработать урок Метод замены в неопределенном интеграле. ЭТО ВАЖНЕЙШИЙ ПРИЁМ! Может быть, даже самая важная статья из всех моих статей, посвященных интегралам. И, в-третьих, обязательно следует  ознакомиться с методом интегрирования по частям, поскольку с помощью него интегрируется обширный класс функций. Если Вы освоите хотя бы эти три урока, то уже «не два». Вам могут «простить» незнание интегралов от тригонометрических функций, интегралов от дробей, интегралов от дробно-рациональных функций, интегралов от иррациональных функций (корней), но вот если «сесть в лужу» на методе замены или методе интегрирования по частям – то это будет очень и очень скверно.

В Рунете сейчас весьма распространены демотиваторы. В контексте изучения интегралов, наоборот, просто необходим  МОТИВАТОР. Как в том анекдоте про Василия Ивановича, который и Петьку мотивировал, и Аньку мотивировал. Уважаемые лентяи, халявщики и другие нормальные студенты, обязательно прочитайте нижеследующее. Знания и навыки по неопределенному интегралу потребуются в дальнейшей учебе, в частности, при изучении определенного интеграла, несобственных интегралов, дифференциальных уравнений на 2 курсе. Необходимость взять интеграл возникает даже в теории вероятностей! Таким образом, без интегралов путь на летнюю сессию и 2 курс БУДЕТ РЕАЛЬНО ЗАКРЫТ. Я серьезно. Вывод таков. Чем больше интегралов различных типов вы прорешаете, тем легче будет дальнейшая жизнь. Да, это займет довольно много времени, да, порой, не хочется, да, иногда «да фиг с ним, с этим интегралом, авось не попадется». Но, воодушевлять и греть душу должна следующая мысль, ваши усилия окупятся сполна! Вы будете, как орехи щелкать дифференциальные уравнения и легко расправляться с интегралами, которые встретятся в других разделах высшей математики. Качественно разобравшись с неопределенным интегралом, ВЫ ФАКТИЧЕСКИ ОСВАИВАЕТЕ ЕЩЕ НЕСКОЛЬКО РАЗДЕЛОВ ВЫШКИ.

И поэтому я просто не мог не создать интенсивный курс по технике интегрирования, который получился на удивление коротким – желающие могут воспользоваться pdf-книгой и подготовиться ОЧЕНЬ быстро. Но материалы сайта ни в коем случае не хуже!

Итак, начинаем с простого. Посмотрим на таблицу интегралов. Как и в производных, мы замечаем несколько правил интегрирования и таблицу интегралов от некоторых элементарных функций. Нетрудно заметить, что любой табличный интеграл (да и вообще любой неопределенный интеграл) имеет вид:

Сразу разбираемся в обозначениях и терминах:

– значок интеграла.

 – подынтегральная функция (пишется с буквой «ы»).

 – значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.

 – подынтегральное выражение или «начинка» интеграла.

 – первообразная функция.

 – множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа .

Решить интеграл – это значит найти определенную функцию , пользуясь некоторыми правилами, приемами и таблицей.

Еще раз посмотрим на запись:

Посмотрим в таблицу интегралов.

Что происходит? Левые части  у нас превращаются в другие функции: .

Упростим наше определение.

Решить неопределенный интеграл  – это значит ПРЕВРАТИТЬ его в определенную функцию , пользуясь некоторыми правилами, приемами и таблицей.

Возьмем, например, табличный интеграл . Что произошло?  превратился в функцию .

Как и в случае с производными, для того, чтобы научиться находить интегралы, не обязательно быть в курсе, что такое интеграл, первообразная функция с теоретической точки зрения. Достаточно просто осуществлять превращения по некоторым формальным правилам. Так, в случае  совсем не обязательно понимать, почему интеграл превращается именно в . Пока можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны.

Так как дифференцирование и интегрирование – противоположные операции, то для любой первообразной, которая найдена правильно, справедливо следующее:

Иными словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция.

Вернемся к тому же табличному интегралу .

Убедимся в справедливости данной формулы. Берем производную от правой части:

 – исходная подынтегральная функция.

Вот, кстати, стало понятнее, почему к функции  всегда приписывается константа . При дифференцировании константа всегда превращается в ноль.

Решить неопределенный интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию. В рассматриваемом табличном примере , , ,  и т. д. – все эти функции являются решением интеграла . Решений бесконечно много, поэтому записывают коротко:

Таким образом, любой неопределенный интеграл достаточно легко проверить (в отличие от производных, где хорошую стопудовую проверку можно осуществить разве что с помощью математических программ). Это некоторая компенсация за большое количество интегралов разных видов.

Переходим к рассмотрению конкретных примеров. Начнем, как и при изучении производной,
с двух правил интегрирования, которые также называют свойствами линейности неопределенного интеграла:

 – постоянный множитель можно (и нужно) вынести за знак интеграла.

 – интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.

Как видите, правила, в принципе, такие же, как и для производных.

Пример 1

Найти неопределенный интеграл. Выполнить проверку.

Решение: Удобнее переписать его на бумагу.

(1) Применяем правило . Не забываем записать значок дифференциала  под каждым интегралом. Почему под каждым?  – это полноценный множитель, если расписывать решение совсем детально, то первый шаг следует записать так:

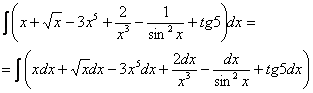
(2) Согласно правилу , выносим все константы за знаки интегралов. Обратите внимание, что в последнем слагаемом  – это константа, её также выносим.
Кроме того, на данном шаге готовим корни и степени для интегрирования. Точно так же, как и при дифференцировании, корни надо представить в виде . Корни и степени, которые располагаются в знаменателе – перенести вверх.

! Примечание: в отличие от производных, корни в интегралах далеко не всегда следует приводить к виду , а степени переносить вверх. Например,  – это готовый табличный интеграл, и всякие китайские хитрости вроде  совершенно не нужны. Аналогично: – тоже табличный интеграл, нет никакого смысла представлять дробь  в виде .  Внимательно изучите таблицу!

(3) Все интегралы у нас табличные. Осуществляем превращение с помощью таблицы, используя формулы: ,  и .
Особое внимание обращаю на формулу интегрирования степенной функции , она встречается очень часто, ее лучше запомнить. Следует отметить, что табличный интеграл  – частный случай этой же формулы: .
Константу  достаточно приплюсовать один раз в конце выражения (а не ставить их после каждого интеграла).
(4) Записываем полученный результат в более компактном виде, все степени вида  снова представляем в виде корней, степени с отрицательным показателем – сбрасываем обратно в знаменатель.

Проверка. Для того чтобы выполнить проверку нужно продифференцировать полученный ответ:

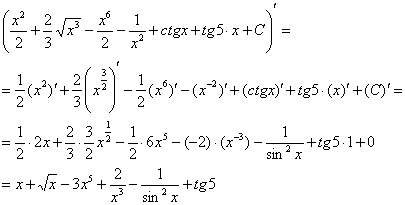
Получена исходная подынтегральная функция, значит, интеграл найден правильно. От чего плясали, к тому и вернулись. Знаете, очень хорошо, когда история с интегралом заканчивается именно так.

Время от времени встречается немного другой подход к проверке неопределенного интеграла, от ответа берется не производная, а дифференциал:

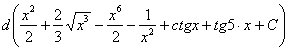
Кто с первого семестра понял, тот понял, но сейчас нам важны не теоретические тонкости, а важно то, что с этим дифференциалом дальше делать. Его необходимо раскрыть, и с формально-технической точки зрения – это почти то же самое, что найти производную. Дифференциал раскрывается следующим образом: значок  убираем, справа над скобкой ставим штрих, в конце выражения приписываем множитель :

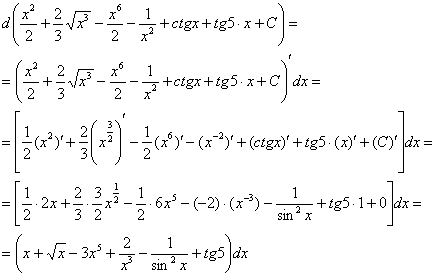
Получено исходное подынтегральное выражение, значит, интеграл найден правильно.

Второй способ проверки мне нравится меньше, так как приходится дополнительно рисовать большие скобки и тащить значок дифференциала  до конца проверки. Хотя он корректнее или «солиднее» что ли.

На самом деле я вообще мог умолчать о втором способе проверки. Дело не в способе, а в том, что мы научились раскрывать дифференциал. Еще раз.

Дифференциал раскрывается следующим образом:

1) значок  убираем;
2) справа над скобкой ставим штрих (обозначение производной);
3) в конце выражения приписываем множитель .

Например:

Запомните это. Рассмотренный приём потребуется нам очень скоро.

Пример 2

Найти неопределенный интеграл. Выполнить проверку.

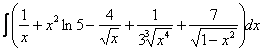
Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

Когда мы находим неопределенный интеграл, то ВСЕГДА стараемся сделать проверку, тем более, для этого есть прекрасная возможность. Далеко не все типы задач в высшей математике является подарком с этой точки зрения. Неважно, что часто в контрольных заданиях проверки не требуется, её никто, и ничто не мешает провести на черновике. Исключение можно сделать лишь тогда, когда не хватает времени (например, на зачете, экзамене). Лично я всегда проверяю интегралы, а отсутствие проверки считаю халтурой и некачественно выполненным заданием.

Пример 3

Найти неопределенный интеграл. Выполнить проверку.

Решение: Анализируя интеграл, мы видим, что у нас произведение двух функций, да еще и возведение в степень целого выражения. К сожалению, на поприще интегральной битвы нет хороших и удобных формул для интегрирования произведения и частного , .

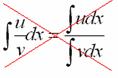А поэтому, когда дано произведение или частное, всегда имеет смысл посмотреть, а нельзя ли преобразовать подынтегральную функцию в сумму?

Рассматриваемый пример – тот случай, когда можно. Сначала я приведу полное решение, комментарии будут ниже.

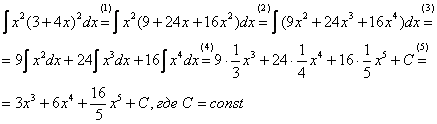
(1) Используем старую-добрую формулу квадрата суммы , избавляясь от степени.

(2) Вносим  в скобку, избавляясь от произведения.

(3) Используем свойства линейности интеграла (оба правила сразу).

(4) Превращаем интегралы по табличной формуле .

(5) Упрощаем ответ. Здесь следует обратить внимание на обыкновенную неправильную дробь  – она несократима и в ответ входит именно в таком виде. Не нужно делить на калькуляторе ! Не нужно представлять ее в виде !

Проверка:

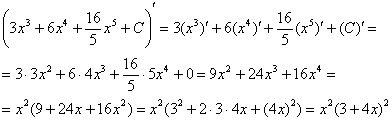
Получена исходная подынтегральная функция, значит, интеграл найден правильно.

В ходе проверки функцию всегда желательно «упаковать» до первоначального вида, вынося в данном случае  за скобки и применяя формулу сокращенного умножения в обратном направлении:

Пример 4

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

Пример 5

Найти неопределенный интеграл. Выполнить проверку.

В данном примере подынтегральная функция представляет собой дробь. Когда мы видим в подынтегральном выражении дробь, то первой мыслью должен быть вопрос: А нельзя ли как-нибудь от этой дроби избавиться, или хотя бы её упростить?

Замечаем, что в знаменателе находится одинокий корень из «икс». Один в поле – не воин, а значит, можно почленно разделить числитель на знаменатель:

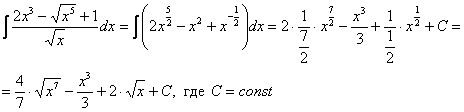
Действия с дробными степенями я не комментирую, так как о них неоднократно шла речь в статьях о производной функции. Если Вас все-таки ставит в тупик такой пример, как , и ни в какую не получается правильный ответ , то рекомендую обратиться к школьным учебникам. В высшей математике дроби и действия с ними встречаются на каждом шагу.

Также обратите внимание, что в решении пропущен один шаг, а именно, применение правил , . Обычно уже при начальном опыте решения интегралов данные свойства считают само собой разумеющимися и не расписывают подробно.

Пример 6

Найти неопределенный интеграл. Выполнить проверку.

Это пример для самостоятельно решения. Ответ и полное решение в конце урока.

В общем случае с дробями в интегралах не всё так просто, дополнительный материал по интегрированию дробей некоторых видов можно найти в статье Интегрирование некоторых дробей.

! Но, прежде чем перейти к вышеуказанной статье, необходимо ознакомиться с уроком Метод замены в неопределенном интеграле. Дело в том, что подведение функции под дифференциал или метод замены переменной является ключевым моментом в изучении темы, поскольку встречается не только «в чистых заданиях на метод замены», но и во многих других разновидностях интегралов.

Очень хотелось включить еще несколько примеров в данный урок, но вот сижу сейчас, печатаю этот текст в Вёрде и замечаю, что статья уже выросла до приличных размеров.
А поэтому вводный курс интегралов для чайников подошел к концу.

Желаю успехов!

Решения и ответы:

Пример 2: Решение:

Пример 4: Решение:

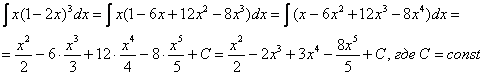
В данном примере мы использовали формулу сокращенного умножения

Пример 6: Решение:

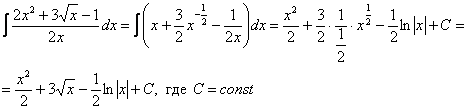
Я выполнил проверку, а Вы? ;)

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте