


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Ортогональное преобразование квадратичной формы
На этом уроке мы продолжим приводить квадратичную форму (1-е занятие) к каноническому виду (2-е занятие), и помимо нового метода приведения, рассмотрим геометрический смысл темы и важное практическое приложение – о том, как привести линию второго порядка к каноническому виду с помощью ортогонального преобразования квадратичной формы.
Сначала расскажу суть метода в общем виде. Ничего страшного, если что-то будет не понятно – всё разберём на конкретных примерах.
Любую квадратичную форму ![]() с действительными (как мы оговорили) коэффициентами
с действительными (как мы оговорили) коэффициентами  можно привести к каноническому виду:
можно привести к каноническому виду:
![]() , где
, где ![]() – собственные числа матрицы
– собственные числа матрицы ![]() (тоже действительные).
(тоже действительные).
Такое приведение осуществляется с помощью линейного преобразования (замен):
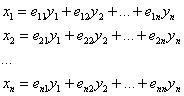 , коэффициенты которого (по столбцам!) – есть координаты соответствующих ортонормированных собственных векторов матрицы
, коэффициенты которого (по столбцам!) – есть координаты соответствующих ортонормированных собственных векторов матрицы ![]() :
:
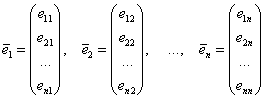
Данные векторы нормированы (имеют единичную длину) и попарно ортогональны (грубо говоря, перпендикулярны); отсюда и название – метод ортогонального преобразования.
Напоминаю распространённую матричную запись ![]() , где:
, где:
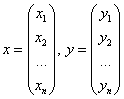 и
и  – матрица ортогонального преобразования.
– матрица ортогонального преобразования.
Посмотрим, как работает метод в простейшем случае:
Пример 10
Это не опечатка – пример уже десятый!
Привести квадратичную форму к каноническому виду методом ортогонального преобразования
![]()
Найти матрицу соответствующего преобразования.
Решение: запишем матрицу формы ![]() и из уравнения
и из уравнения ![]() найдём её собственные числа:
найдём её собственные числа:
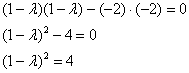
Очевидно, что ![]() , таким образом:
, таким образом:
![]() – квадратичная форма
– квадратичная форма ![]() в каноническом виде.
в каноническом виде.
Найдём соответствующее линейное преобразование. Для этого нужно отыскать собственные векторы матрицы ![]() :
:
1) Если ![]() , то получаем систему линейных уравнений:
, то получаем систему линейных уравнений:
![]() , откуда следует, что
, откуда следует, что ![]() .
.
Полагая ![]() , запишем первый собственный вектор:
, запишем первый собственный вектор: ![]() – координаты удобно записывать именно в столбец! Сразу вычислим длину вектора (скоро потребуется):
– координаты удобно записывать именно в столбец! Сразу вычислим длину вектора (скоро потребуется):
![]()
2) Если ![]() , то имеем систему:
, то имеем систему:
![]() , из которой следует, что
, из которой следует, что ![]()
Пусть ![]() , тогда
, тогда ![]() и
и ![]() – второй собственный вектор. Его длина:
– второй собственный вектор. Его длина:
![]()
Если матрица формы имеет различные собственные числа, то соответствующие собственные векторы попарно ортогональны. Убедимся в справедливости этого утверждения для нашей пары, вычислив их скалярное произведение:
![]()
Поскольку длины векторов ![]() не равны единице, то их нужно нормировать, т.е. найти коллинеарные им векторы
не равны единице, то их нужно нормировать, т.е. найти коллинеарные им векторы ![]() единичной длины. Для этого каждую координату собственного вектора делим на его длину:
единичной длины. Для этого каждую координату собственного вектора делим на его длину:
– координаты ![]() на
на 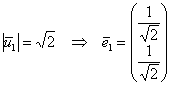 ;
;
– координаты ![]() на
на 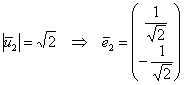 .
.
Такую задачу мы решали в курсе аналитической геометрии на уроке… да, на уроке Уравнение плоскости (Пример 5), но сейчас речь идёт, подчёркиваю, о векторах в их алгебраическом смысле.
Проверим, что длины полученных векторов действительно равны единице:
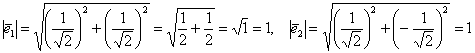 , ч.т.п.
, ч.т.п.
Теперь последовательно помещаем координаты векторов 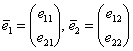 в столбцы матрицы:
в столбцы матрицы: 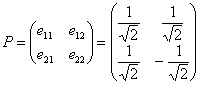 – это и есть матрица выполненного ортогонального преобразования, в строках которой находятся «игрековые» коэффициенты линейных замен:
– это и есть матрица выполненного ортогонального преобразования, в строках которой находятся «игрековые» коэффициенты линейных замен: 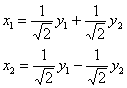 .
.
Ответ: ![]() ,
, 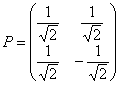
Полученный результат можно проверить:
1) непосредственной подстановкой 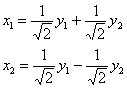 в форму
в форму ![]() :
:
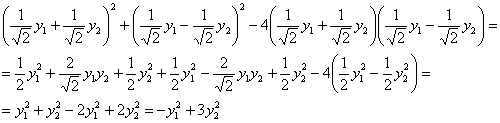
2) либо с помощью знакомой формулы:
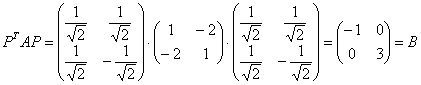 – получив «каноничную» матрицу.
– получив «каноничную» матрицу.
Справка: матрица ортогонального преобразования квадратичной формы относится к классу так называемых ортогональных матриц (Вики), которые встречаются не только в этой теме. Ортогональная матрица обладает рядом интересных свойств, в частности, её определитель равен +1 либо –1, а транспонированная матрица совпадает с обратной матрицей.
А сейчас обратим внимание на следующий момент: канонический вид ![]() и алгоритм решения никак не регламентируют порядок расположения собственных чисел, и поэтому форму можно привести к такому виду не единственным способом. Так, если в прорешанном примере перечислить собственные числа в другом порядке:
и алгоритм решения никак не регламентируют порядок расположения собственных чисел, и поэтому форму можно привести к такому виду не единственным способом. Так, если в прорешанном примере перечислить собственные числа в другом порядке: ![]() (никто ж не запрещает), то получится другой, тоже канонический вид
(никто ж не запрещает), то получится другой, тоже канонический вид ![]() . При этом нормированные собственные векторы меняются местами:
. При этом нормированные собственные векторы меняются местами: 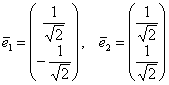 и матрица линейного преобразования будет другой:
и матрица линейного преобразования будет другой: 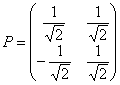 . В строках этой матрицы находятся «игрековые» коэффициенты соответствующих линейных замен:
. В строках этой матрицы находятся «игрековые» коэффициенты соответствующих линейных замен:
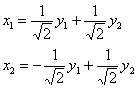
Желающие могут выполнить прямую подстановку в ![]() и «на выходе» получить
и «на выходе» получить ![]() .
.
Теперь рассмотрим эту же квадратичную форму в геометрической «ипостаси». Для понимания следующего примера нужно ориентироваться (хотя бы в общих чертах) в линиях второго порядка:
Пример 11
С помощью теории квадратичных форм привести уравнение линии второго порядка к каноническому виду
![]()
Иными словами, нам нужно выяснить, какую линию задаёт это уравнение (эллипс, гиперболу, параболу или какую-то другую) и записать его в каноническом виде. В курсе аналитической геометрии мы рассмотрели «традиционные» методы приведения, и вот сейчас познакомимся с ещё одним способом.
Начало решения практически совпадает с предыдущей задачей, с той поправкой, что там фигурировали переменные ![]() и
и ![]() , а в геометрии обычно используют
, а в геометрии обычно используют ![]() («старые» переменные) и
(«старые» переменные) и ![]() («новые» переменные – штрихи здесь не имеют никакого отношения к производным).
(«новые» переменные – штрихи здесь не имеют никакого отношения к производным).
Итак, на первом шаге рассматриваем квадратичную форму ![]() , записываем её матрицу и находим её собственные числа. После чего возникает недавний вопрос – в каком порядке их следует перечислить:
, записываем её матрицу и находим её собственные числа. После чего возникает недавний вопрос – в каком порядке их следует перечислить: ![]() или
или ![]() ? Когда мы просто приводили форму к каноническому виду, это не имело значения. Но вот тут имеет.
? Когда мы просто приводили форму к каноническому виду, это не имело значения. Но вот тут имеет.
В первом случае у нас получится уравнение ![]() , во втором:
, во втором: ![]() . Оба уравнения задают гиперболу, однако канонический вид имеет только второе уравнение. Таким образом, нас устраивает «комплект»
. Оба уравнения задают гиперболу, однако канонический вид имеет только второе уравнение. Таким образом, нас устраивает «комплект» ![]() , но НЕ ФАКТ, что подойдет найденное преобразование
, но НЕ ФАКТ, что подойдет найденное преобразование 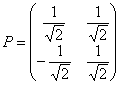 .
.
Дело в том, что ортонормированные собственные векторы можно выбрать ещё тремя способами: ![]() или
или ![]() , и если бы мы просто приводили форму к каноническому виду, то опять же – нас устроил бы любой из 4 вариантов. Но не сейчас.
, и если бы мы просто приводили форму к каноническому виду, то опять же – нас устроил бы любой из 4 вариантов. Но не сейчас.
По той причине, что линейные преобразования должны соответствовать формулам формулами поворота ![]() декартовой системы координат
декартовой системы координат ![]() на угол «фи». Этот факт справедлив только в том случае, если определитель матрицы преобразования равен «плюс» единице:
на угол «фи». Этот факт справедлив только в том случае, если определитель матрицы преобразования равен «плюс» единице: ![]() .
.
Проверяем: 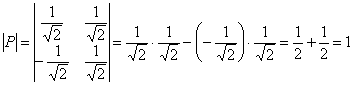 , таким образом, нам повезло, и преобразование
, таким образом, нам повезло, и преобразование 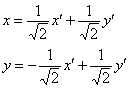 действительно подходит под шаблон
действительно подходит под шаблон ![]() .
.
Значениям ![]() соответствует табличный угол
соответствует табличный угол ![]() , но привычнее, конечно, говорить об угле
, но привычнее, конечно, говорить об угле ![]() .
.
Таким образом, поворачивая систему ![]() на 45 градусов по часовой стрелке, мы переходим от уравнения
на 45 градусов по часовой стрелке, мы переходим от уравнения ![]() в старой системе координат к каноническому уравнению
в старой системе координат к каноническому уравнению ![]() в новой системе координат
в новой системе координат ![]() :
:
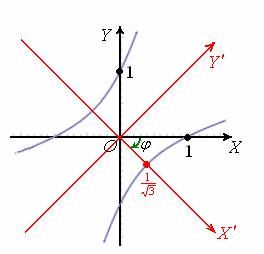
Наклоните голову вправо на 45 градусов и убедитесь, что в «красной» системе координат гипербола действительно имеет канонический вид.
Кроме того, нас устроило бы ещё одно преобразование: 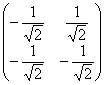 . Легко видеть, что его определитель равен «плюс» единице и формулам
. Легко видеть, что его определитель равен «плюс» единице и формулам 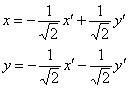 соответствует поворот системы
соответствует поворот системы ![]() на
на ![]() против часовой стрелки. В этом случае оси
против часовой стрелки. В этом случае оси ![]() будут «смотреть» в противоположные стороны и гипербола тоже окажется в каноническом положении. Желающие могут повернуть голову влево на 135 градусов и приобщиться к прекрасному :)
будут «смотреть» в противоположные стороны и гипербола тоже окажется в каноническом положении. Желающие могут повернуть голову влево на 135 градусов и приобщиться к прекрасному :)
Ответ: ![]()
Что произойдёт, если квадратичную форму ![]() приводить к каноническому виду методом Лагранжа? В общем случае будут получаться другие гиперболы. Но гиперболы! И вообще – любое невырожденное линейное преобразование данной формы будет приводить нас к уравнениям гипербол, и только к ним – как я отмечал в конце предыдущего урока, такое преобразование не меняет СУЩНОСТИ формы.
приводить к каноническому виду методом Лагранжа? В общем случае будут получаться другие гиперболы. Но гиперболы! И вообще – любое невырожденное линейное преобразование данной формы будет приводить нас к уравнениям гипербол, и только к ним – как я отмечал в конце предыдущего урока, такое преобразование не меняет СУЩНОСТИ формы.
Таким образом, метод Лагранжа – это «быстрый» способ узнать, что это за линия, но вот сохранение её размеров нам гарантирует лишь ортогональное преобразование.
Ортогональное линейное преобразование переводит ортонормированный базис в другой ортонормированный базис и сохраняет размеры объектов. Это справедливо для пространства любой размерности, и, кроме того, применимо не только к квадратичным формам – ортогональному преобразованию (Вики) посвящена отдельная тема высшей алгебры, и интересующихся я отсылаю к соответствующим источникам информации.
Следующий пример для самостоятельного решения:
Пример 12
Привести квадратичную форму к каноническому виду методом ортогонального преобразования.
![]()
Решить задачу двумя способами (переставляя собственные числа) и записать матрицы соответствующих линейных преобразований.
После чего мы продолжим банкет родственной геометрической задачей:
Пример 13
![]()
Данную линию мы уже приводили к каноническому виду (Пример 1) и сейчас сделаем то же самое, используя новый метод.
Надеюсь все прорешали предыдущее задание, поскольку начало решения будет совпадать с точностью до обозначений, и нам осталось выбрать подходящее преобразование:
![]()
или
![]()
Очевидно, здесь получится уравнение эллипса ![]() , и чтобы выдерживалось неравенство полуосей, нам подойдёт МЕНЬШИЙ коэффициент при переменной «икс штрих», то есть, следует выбрать первый вариант:
, и чтобы выдерживалось неравенство полуосей, нам подойдёт МЕНЬШИЙ коэффициент при переменной «икс штрих», то есть, следует выбрать первый вариант:
![]()
В своём образце решения я сразу выбрал подходящее преобразование
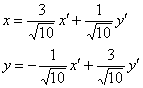 , определяющее поворот на угол
, определяющее поворот на угол ![]() , но у вас мог получиться и любой другой их трёх оставшихся случаев (в зависимости от выбора собственных векторов).
, но у вас мог получиться и любой другой их трёх оставшихся случаев (в зависимости от выбора собственных векторов).
Преобразование 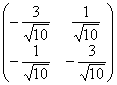 тоже приемлемо (поворот примерно на
тоже приемлемо (поворот примерно на ![]() ), а вот
), а вот 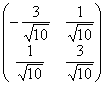 и
и 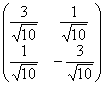 непригодны, так как не соответствуют формулам
непригодны, так как не соответствуют формулам ![]() .
.
Итак, в результате замен 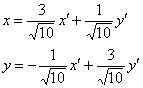 исходное уравнение
исходное уравнение ![]() преобразуется к виду:
преобразуется к виду:
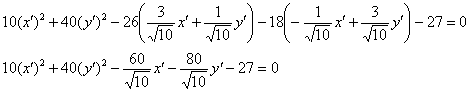
Данное уравнение задаёт тот же самый эллипс в системе ![]() (зелёный цвет), которая получена поворотом системы
(зелёный цвет), которая получена поворотом системы ![]() на угол
на угол ![]() :
:
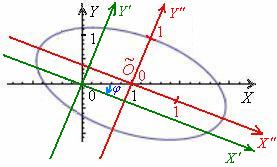
Осталось провести параллельный перенос координатных осей. Выделяем полные квадраты:
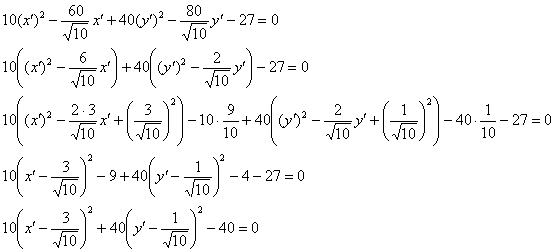
И в результате замен ![]() получаем каноническое уравнение эллипса в «красной» системе
получаем каноническое уравнение эллипса в «красной» системе ![]() :
:
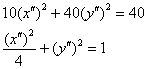
Ответ: ![]()
Но для решения этой задачи, конечно, выгоднее метод инвариантов.
Самостоятельно решите Пример 3 того же урока, которому была посвящена целая мыльная опера с несколькими чертежами:
Пример 14
![]() – привести уравнение линии к каноническому виду с помощью ортогонального преобразования квадратичной формы.
– привести уравнение линии к каноническому виду с помощью ортогонального преобразования квадратичной формы.
Следует отметить, что здесь нас устроит всего лишь одно преобразование из четырёх, поскольку перед нами парабола, и в каноническом положении она «смотрит» в одну, строго определённую сторону.
Краткое решение и ответ в конце урока. Любопытно, что тут решение, наоборот – получилось заметно проще, чем «классическим» геометрическим методом. Ну и конечно, подарок, если нужно выполнить только один поворот, как в Примере 11.
Кстати, как быстро и даже устно определить тип линии? Если определитель матрицы формы 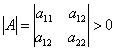 , то перед нами линия эллиптического типа (эллипс, мнимый эллипс или пара мнимых пересекающихся прямых), если
, то перед нами линия эллиптического типа (эллипс, мнимый эллипс или пара мнимых пересекающихся прямых), если ![]() – то гиперболического (гипербола или пара пересекающихся прямых), и если
– то гиперболического (гипербола или пара пересекающихся прямых), и если ![]() – то параболического (парабола, пара параллельных (мнимых или обычных) или пара совпавших прямых).
– то параболического (парабола, пара параллельных (мнимых или обычных) или пара совпавших прямых).
На этой позитивной ноте перейдём к квадратичным формам трёх переменных:
Пример 15
Привести квадратичную форму к каноническому виду методом ортогонального преобразования
![]()
Найти соответствующее преобразование
Решение начинается точно так же: запишем матрицу формы 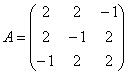 и найдём её собственные числа:
и найдём её собственные числа:
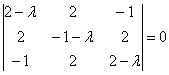
определитель раскрою по 1-й строке:
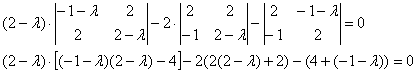
напоминаю полезный технический приём – в первом слагаемом, где нам светит «лямбда в кубе», не нужно спешить раскрывать скобки:
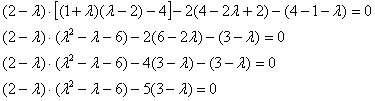
решив квадратное уравнение, раскладываем трёхчлен на множители:
![]()
таким образом, нам удалось избавиться от многочлена 3-й степени, отыскание корней которого – есть непростая задача. И теперь такой задачи нет:
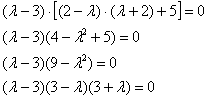
Порядок собственных чисел не имеет значения, и поэтому я выберу вариант:
![]() – чтобы красивее записать канонический вид:
– чтобы красивее записать канонический вид:
![]()
Найдём ортогональное линейное преобразование. Сложность задачи состоит в том, что если среди собственных чисел есть кратные, то ортогональность найденных собственных векторов не гарантирована, и в «неудачном» случае нам придётся предпринять меры по их ортогонализации. Впрочем, не будем торопить события:
1-2) Если ![]() , то получаем систему:
, то получаем систему:
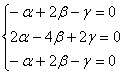 , которая фактически состоит из одного уравнения.
, которая фактически состоит из одного уравнения.
Выберем в качестве базисной переменную «альфа» и выразим её через свободные переменные: ![]() . Запишем общее решение в столбец:
. Запишем общее решение в столбец:
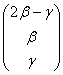
Теперь нам нужно найти векторы фундаментальной системы. Для значений ![]() получаем:
получаем:
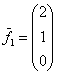 – первый вектор фундаментальной системы;
– первый вектор фундаментальной системы;
и для ![]() :
:
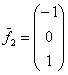 – второй вектор.
– второй вектор.
Легко видеть, что оба вектора удовлетворяют системе (уравнению ![]() ) и, естественно, являются собственными. Вычислим их скалярное произведение:
) и, естественно, являются собственными. Вычислим их скалярное произведение:
![]() , значит, данные векторы НЕ ортогональны, что нас не устраивает.
, значит, данные векторы НЕ ортогональны, что нас не устраивает.
Поэтому эту пару векторов следует ортогонализовать. Поскольку любая линейная комбинация векторов фундаментальной системы тоже является решением системы (уравнения ![]() ), то рассмотрим вектор
), то рассмотрим вектор ![]() , где
, где ![]() – пока ёщё неизвестный числовой коэффициент, и составим следующее скалярное произведение, которое должно быть равно нулю:
– пока ёщё неизвестный числовой коэффициент, и составим следующее скалярное произведение, которое должно быть равно нулю:
![]()
по свойствам скалярного произведения:
![]()
откуда выражаем и находим:
![]()
Таким образом, в качестве первого собственного вектора выбираем:
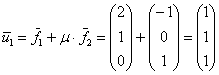
и в качестве второго:
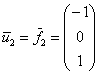
Как на ладони видно:
![]() – что полученные векторы действительно ортогональны
– что полученные векторы действительно ортогональны
С третьим собственным вектором всё прозрачно:
3) Если ![]() , то получаем систему:
, то получаем систему:
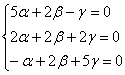 из 2-го уравнения выразим
из 2-го уравнения выразим ![]() – подставим в 1-е и 3-е уравнения:
– подставим в 1-е и 3-е уравнения:
![]()
Пусть ![]()
Таким образом, третий собственный вектор: 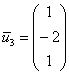 . Не забываем о проверке – устно или на черновике подставляем его координаты в каждое уравнение системы.
. Не забываем о проверке – устно или на черновике подставляем его координаты в каждое уравнение системы.
И проверяем, ортогонален ли он ранее найденным векторам 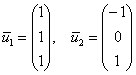 :
:
![]()
Отлично. Осталось вычислить длины векторов и при необходимости их нормировать:
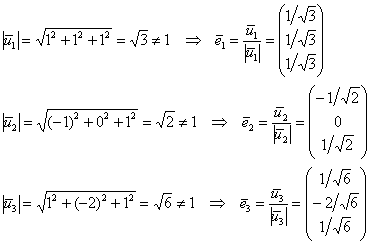
Таким образом, матрица ортогонального преобразования:
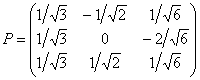
Запишем ответ: ![]() и преобразование в виде прямых замен:
и преобразование в виде прямых замен:
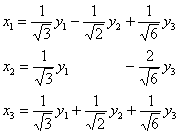
Но подставлять всё это в ![]() что-то не хочется :) Однако, проверка нужна, и мне проще воспользоваться матричным калькулятором:
что-то не хочется :) Однако, проверка нужна, и мне проще воспользоваться матричным калькулятором:
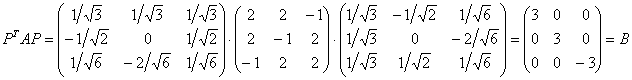
Засёк для интереса время, «забивка» матриц и вычисления заняли ровно 2 минуты.
И здесь есть ещё один интересный момент. В рассмотренной задаче векторы фундаментальной системы можно выбрать бесчисленным количеством способов, и поэтому мы можем построить бесконечно много ортогональных преобразований, которые приводят форму к виду ![]() . Но так бывает, конечно, не всегда.
. Но так бывает, конечно, не всегда.
В заключение статьи кратко расскажу о геометрическом смысле ортогонального преобразования формы трёх переменных. Даже добавлять константу не буду:
![]() – данное уравнение определяет некоторую поверхность второго порядка в «школьном» базисе
– данное уравнение определяет некоторую поверхность второго порядка в «школьном» базисе ![]() . Что это за поверхность – скажет разве что вундеркинд.
. Что это за поверхность – скажет разве что вундеркинд.
Проведённое ортогональное преобразование осуществляет переход к другому ортонормированному базису ![]() – ТАКОМУ, в котором данная поверхность имеет канонический вид:
– ТАКОМУ, в котором данная поверхность имеет канонический вид:
![]() – откуда сразу понятно, что это коническая поверхность, причём, ортогональное преобразование сохранило её размеры. Кстати, перед нами конус вращения, и теперь стало ясно, почему существует бесконечно много пригодных ортогональных преобразований: связку векторов
– откуда сразу понятно, что это коническая поверхность, причём, ортогональное преобразование сохранило её размеры. Кстати, перед нами конус вращения, и теперь стало ясно, почему существует бесконечно много пригодных ортогональных преобразований: связку векторов ![]() мы можем «повернуть в горизонтальной плоскости» как угодно, и во всех полученных базисах
мы можем «повернуть в горизонтальной плоскости» как угодно, и во всех полученных базисах ![]() коническая поверхность будет иметь канонический вид.
коническая поверхность будет иметь канонический вид.
Саму же разновидность поверхности можно выяснить быстрее – методом Лагранжа, но он в общем случае будет «показывать» нам конусы других размеров.
И задача для самостоятельного решения, тоже с кратными собственными числами, ибо с разными получится как-то совсем скучно:
Пример 16
Найти ортогональные линейные замены, приводящие форму к каноническому виду
![]()
Не пропускайте, это несколько другой тип ;) Да и вычислений заметно меньше.
Для квадратичных форм четырёх и бОльшего количества переменных задача ортогонального преобразования решается по аналогии. Но в учебной практике такие примеры редкость ввиду их вычислительной сложности, и поэтому я завершаю эту увлекательную тему.
Квадратичные формы – держат нас в форме!
Решения и ответы:
Пример 12. Решение: запишем матрицу формы ![]() и найдём её собственные числа:
и найдём её собственные числа:
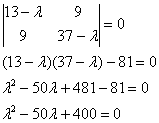
Решим квадратное уравнение:
![]()
![]() – собственные числа, таким образом:
– собственные числа, таким образом:
![]() – форма
– форма ![]() – в каноническом виде.
– в каноническом виде.
Найдём собственные векторы, их длины и при необходимости выполним нормирование:
1) Если ![]() , то:
, то:
![]() , пусть
, пусть ![]()
Таким образом: ![]()
![]() .
.
Разделим каждую координату на длину: 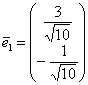
2) Если ![]() , то:
, то:
![]() , пусть
, пусть ![]()
Таким образом: ![]()
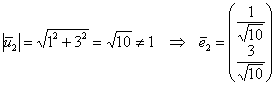
Таким образом, матрица линейного преобразования:
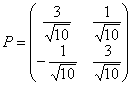
Выполним проверку прямой подстановкой 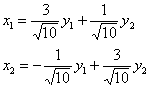 в
в ![]() :
:
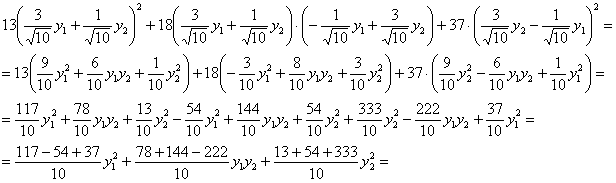
![]() , что и требовалось проверить.
, что и требовалось проверить.
Ответ: ![]() ,
, 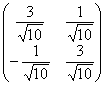 , в случае перестановки собственных чисел:
, в случае перестановки собственных чисел:
![]() ,
, 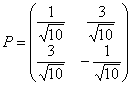
Пример 14. Решение: запишем матрицу ![]() квадратичной формы и найдём её собственные числа:
квадратичной формы и найдём её собственные числа:
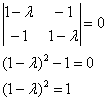
так как каноничная парабола определяется уравнением ![]() , то нам нужно перечислить собственные числа в следующем порядке:
, то нам нужно перечислить собственные числа в следующем порядке:
![]()
Таким образом, квадратичная форма преобразуется к виду:
![]() .
.
Найдём собственные векторы и при необходимости выполним их нормирование:
1) Если ![]() , то:
, то:
![]() , пусть
, пусть ![]()
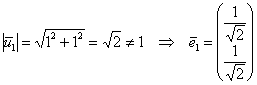
2) Если ![]() , то:
, то:
![]() , пусть
, пусть ![]()
Примечание: вектор ![]() в пару к
в пару к ![]() не годится, т.к. линейное преобразование не будет соответствовать формулам поворота.
не годится, т.к. линейное преобразование не будет соответствовать формулам поворота.
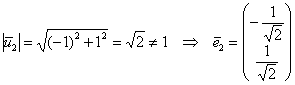
Таким образом, матрица линейного преобразования:
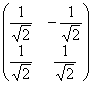 , которое по формулам
, которое по формулам 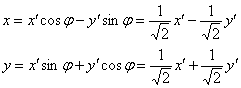 приводит уравнение к виду:
приводит уравнение к виду:
![]()
Однако, после раскрытия скобок, выясняется, что знак при переменной ![]() не приведёт нас каноническому виду
не приведёт нас каноническому виду ![]() .
.
И поэтому нужно выбрать другое преобразование, определитель которого ![]() . Этому критерию подходит пара ортонормированных векторов
. Этому критерию подходит пара ортонормированных векторов 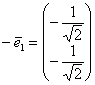 ,
, 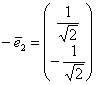 , задающая преобразование
, задающая преобразование 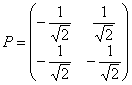 с поворотом
с поворотом 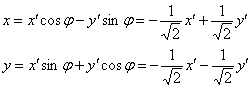 на
на ![]() рад. (–135 градусов) (это угол табличный: значениям
рад. (–135 градусов) (это угол табличный: значениям ![]() соответствует
соответствует ![]() или
или ![]() рад.)
рад.)
Таким образом, данное преобразование приводит нас к уравнению:
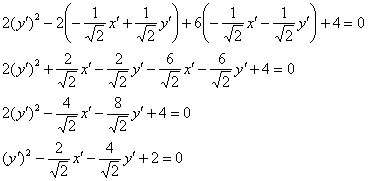
избавимся от иррациональности в знаменателях, домножив числители и знаменатели на ![]() :
:
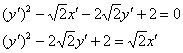
«собираем» полный квадрат при переменной ![]() :
:
![]() и проводим замены
и проводим замены ![]() .
.
Ответ: ![]()
Пример 16. Решение запишем матрицу формы 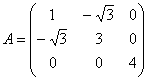 и найдём её собственные числа:
и найдём её собственные числа:
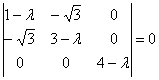
определитель выгодно раскрыть по 3-й строке или 3-му столбцу:
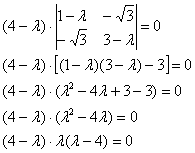
![]() – собственные числа, таким образом:
– собственные числа, таким образом:
![]() – форма
– форма ![]() в каноническом виде.
в каноническом виде.
Найдём собственные векторы:
1-2) Если ![]() , то получаем систему:
, то получаем систему:
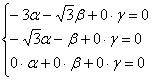 , из которой очевиден собственный вектор
, из которой очевиден собственный вектор 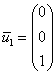 .
.
Второй вектор найдём для ![]() из соотношения
из соотношения ![]() .
.
Пусть 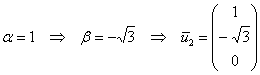
![]()
3) Если ![]() , то:
, то:
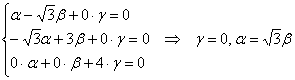
Пусть 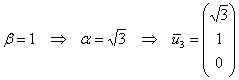
Проверим, что полученный вектор ортогонален двум первым векторам:
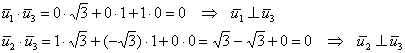
Первый вектор уже имеет единичную длину, поэтому:
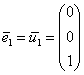
другие векторы нужно нормировать:
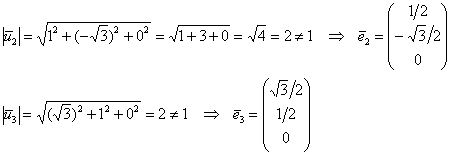
Таким образом, матрица ортогонального преобразования:
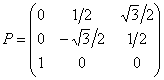
Ответ: 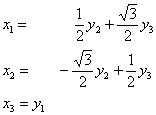
Проверим результат прямой подстановкой в форму ![]() :
:
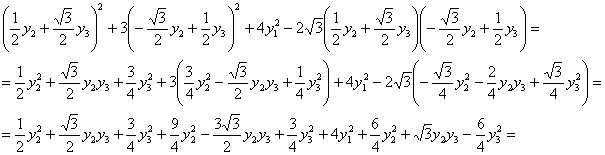
сгруппируем вместе и приведём подобные слагаемые:
![]()
![]() , что и требовалось проверить.
, что и требовалось проверить.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright