


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Наибольшее и наименьшее значения функции на отрезке
Миниатюрная и довольно простая задача из разряда тех, которые служат спасательным кругом плавающему студенту. На природе сонное царство середины июля, поэтому самое время устроиться с ноутбуком на пляже. Ранним утром заиграл солнечный зайчик теории, чтобы в скором времени сфокусироваться на практике, которая, несмотря на заявленную лёгкость, содержит осколки стекла в песке. В этой связи рекомендую добросовестно рассмотреть немногочисленные примеры этой странички. Для решения практических заданий нужно уметь находить производные и понимать материал статьи Интервалы монотонности и экстремумы функции.
Сначала коротко о главном. На уроке о непрерывности функции я приводил определение непрерывности в точке и непрерывности на интервале. Образцово-показательное поведение функции на отрезке формулируется похожим образом. Функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() если:
если:
1) она непрерывна на интервале ![]() ;
;
2) непрерывна в точке ![]() справа и в точке
справа и в точке ![]() слева.
слева.
Во втором пункте речь зашла о так называемой односторонней непрерывности функции в точке. Существует несколько подходов к её определению, но я буду придерживаться начатой ранее линии:
функция ![]() непрерывна в точке
непрерывна в точке ![]() справа, если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке:
справа, если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке: ![]() . Она же непрерывна в точке
. Она же непрерывна в точке ![]() слева, если определена в данной точке и её левосторонний предел равен значению в этой точке:
слева, если определена в данной точке и её левосторонний предел равен значению в этой точке: ![]()
Представьте, что зелёные точки – это гвозди, на которых закреплена волшебная резинка:
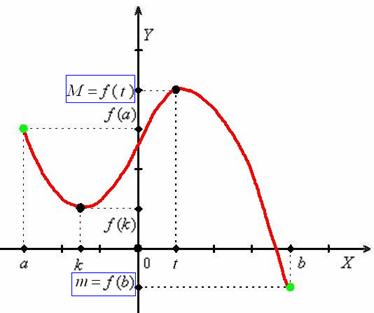
Мысленно возьмите красную линию в руки. Очевидно, что как бы далеко мы не растягивали график вверх и вниз (вдоль оси ![]() ), функция всё равно останется ограниченной – изгородь сверху, изгородь снизу, и наше изделие пасётся в загоне. Таким образом, непрерывная на отрезке функция ограничена на нём. В курсе матанализа сей вроде бы простой факт констатируется и строго доказывается первой теоремой Вейерштрасса. …Многих удивляет, а то и раздражает, что в математике нудно обосновываются «элементарные» утверждения. Однако в этом есть важный смысл. Никто наверняка не знает, что происходит «за горизонтом», в переносном да и в прямом смысле тоже – ведь когда-то и Земля считалась плоской, и для людей это казалось так очевидно и естественно! Впрочем, сейчас мы наблюдаем возрождение античности :)
), функция всё равно останется ограниченной – изгородь сверху, изгородь снизу, и наше изделие пасётся в загоне. Таким образом, непрерывная на отрезке функция ограничена на нём. В курсе матанализа сей вроде бы простой факт констатируется и строго доказывается первой теоремой Вейерштрасса. …Многих удивляет, а то и раздражает, что в математике нудно обосновываются «элементарные» утверждения. Однако в этом есть важный смысл. Никто наверняка не знает, что происходит «за горизонтом», в переносном да и в прямом смысле тоже – ведь когда-то и Земля считалась плоской, и для людей это казалось так очевидно и естественно! Впрочем, сейчас мы наблюдаем возрождение античности :)
Согласно второй теореме Вейерштрасса, непрерывная на отрезке ![]() функция достигает своей точной верхней грани
функция достигает своей точной верхней грани ![]() и своей точной нижней грани
и своей точной нижней грани ![]() .
.
Число ![]() также называют максимальным значением функции на отрезке и обозначают через
также называют максимальным значением функции на отрезке и обозначают через ![]() , а число
, а число ![]() – минимальным значением функции на отрезке с пометкой
– минимальным значением функции на отрезке с пометкой ![]() .
.
В нашем случае:
![]()
![]()
Примечание: в теории распространены записи ![]() (супремум и инфимум, на ломаном русском).
(супремум и инфимум, на ломаном русском).
Грубо говоря, наибольшее значение находится там, где самая высокая точка графика, а наименьшее – где самая низкая точка.
Важно! Как уже заострялось внимание в статье об экстремумах функции, наибольшее значение функции и наименьшее значение функции – НЕ ТО ЖЕ САМОЕ, что максимум функции и минимум функции. Так, в рассматриваемом примере число ![]() является минимумом функции, но не минимальным значением.
является минимумом функции, но не минимальным значением.
Кстати, а что происходит вне отрезка ![]() ? Да хоть потоп, в контексте рассматриваемой задачи это нас совершенно не интересует. Задание предполагает лишь нахождение двух чисел
? Да хоть потоп, в контексте рассматриваемой задачи это нас совершенно не интересует. Задание предполагает лишь нахождение двух чисел ![]() и всё!
и всё!
Более того, решение чисто аналитическое, следовательно, чертежа делать не надо!
Алгоритм лежит на поверхности и напрашивается из приведённого рисунка:
1) Находим значения функции в критических точках, которые принадлежат данному отрезку.
Ловите ещё одну плюшку: здесь отпадает необходимость проверять достаточное условие экстремума, поскольку, как только что было показано, наличие минимума или максимума ещё не гарантирует, что там минимальное или максимальное значение. Демонстрационная функция достигает максимума ![]() и волей судьбы это же число является наибольшим значением функции на отрезке
и волей судьбы это же число является наибольшим значением функции на отрезке ![]() . Но, понятно, такое совпадение имеет место далеко не всегда.
. Но, понятно, такое совпадение имеет место далеко не всегда.
Итак, на первом шаге быстрее и проще вычислить значения функции в критических точках, принадлежащих отрезку, не заморачиваясь есть в них экстремумы или нет.
2) Вычисляем значения функции на концах отрезка.
3) Среди найденных в 1-м и 2-м пунктах значений функции выбираем самое маленькое и самое большое число, записываем ответ.
Садимся на берег синего моря и бьём пятками по мелководью:
Пример 1
Найти наибольшее и наименьшее значения функции ![]() на отрезке
на отрезке ![]()
Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:
![]()
Полученное квадратное уравнение имеет два действительных корня:
![]() – критические точки.
– критические точки.
Ещё раз подчёркиваю, что нас не интересует, есть в них максимумы / минимумы или нет.
Первая критическая точка принадлежит данному отрезку: ![]()
А вот вторая – нет: ![]() , поэтому про неё сразу забываем.
, поэтому про неё сразу забываем.
Вычислим значение функции в нужной точке:
![]()
Итоговый результат я выделил жирным цветом, при оформлении задания от руки его удобно обвести в кружок простым карандашом или пометить как-то по-другому.
2) Вычислим значения функции на концах отрезка:
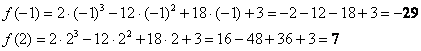
Результаты опять каким-либо образом выделяем.
3) Дело сделано, среди «жирных» чисел выбираем наибольшее и наименьшее.
Ответ: ![]()
Критическое значение ![]() на поверку оказалось точкой максимума, но об этом нас никто не спрашивал. Впрочем, для саморазвития можете устно подмечать такие факты.
на поверку оказалось точкой максимума, но об этом нас никто не спрашивал. Впрочем, для саморазвития можете устно подмечать такие факты.
Пример 2
Найти наибольшее и наименьшее значения функции ![]() на отрезке
на отрезке ![]()
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
В рассматриваемой задаче очень важно не допускать вычислительных ошибок, так как рецензент немедленно посмотрит, сами догадываетесь куда.
Другой существенный момент касается пункта № 1.
Во-первых, критических точек может не оказаться вообще. Это очень хорошо – меньше вычислений. Просто записываем вывод: «критические точки отсутствуют» и переходим ко второму пункту алгоритма.
Во-вторых, все критические точки (одна, две или бОльшее количество) могут не принадлежать отрезку. Замечательно. Пишем следующее: «критические точки (а) не принадлежат (ит) рассматриваемому отрезку». Находить какие-то значения функции здесь, разумеется, тоже не надо.
В моей коллекции есть и те и те примеры, но они унылы как бескрайние просторы Сахары. По сути, всё задание сводится к нахождению двух значений функции на концах интервала. Гораздо интереснее снять кепки, солнечные очки и отправиться играть в пляжный футбол:
Пример 3
Найти наибольшее и наименьшее значения функции на заданном отрезке
![]()
Решение опять начинается дежурной фразой:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:
![]()
Да, критических точек тут и правда целая команда:
![]()
Первые две точки принадлежат нашему отрезку:
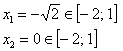
Но третья оказывается вне игры: ![]() , полезно, к слову, запомнить приближённое значение 1,4142 этого исторического корня.
, полезно, к слову, запомнить приближённое значение 1,4142 этого исторического корня.
Вычислим значения функции в подходящих точках:
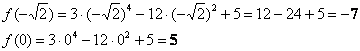
Чтобы не заблудиться в трёх соснах, не забываем выделять результаты.
2) Вычислим значения функции на концах отрезка:
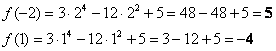
Среди «жирных» чисел выбираем наибольшее и наименьшее значения. Максимальное значение (пятёрка) достигается сразу в двух точках, и это следует указать в ответе:
![]()
Время от времени критические точки могут совпадать с одним или даже с обоими концами отрезка, и в этом случае укорачивается второй этап решения. Следующий пример для самостоятельного изучения посвящен как раз такой ситуации:
Пример 4
Найти наибольшее и наименьшее значения функции на заданном отрезке
![]()
Примерный образец решения в конце урока.
Иногда техническая трудность рассматриваемого задания состоит в замысловатой производной и громоздких вычислениях:
Пример 5
Найти максимальное и минимальное значения функции на отрезке
![]()
Решение: отрезок, надо сказать, творческий, но пример взят из конкретной контрольной работы и ни в коем случае не придуман.
1) Вычислим значения функции в критических точках, которые принадлежат данному отрезку:
![]()
Очевидный корень оказывается не в теме: ![]() .
.
Решаем уравнение:
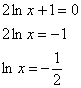
Второй корень принадлежит нашему отрезку: ![]()
Если вам не понятно, почему именно такой корень, обязательно обратитесь к школьному учебнику Алгебра и начала анализа 10-11 класс или нашей Песочнице, ибо плох тот студент, который не мечтает овладеть логарифмами. Дальнейшие вычисления задачи я распишу максимально подробно, но без комментариев.
Вычислим значение функции во второй критической точке:
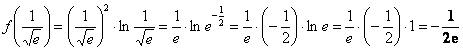
2) Вычислим значения функции на концах отрезка:

3) «Жирные» результаты получены с экспонентами и логарифмами, что существенно затрудняет их сравнение. По сей причине вооружимся калькулятором либо Экселем и вычислим приближённые значения, не забывая, что ![]() :
:
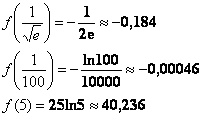
Вот теперь всё понятно.
Ответ: 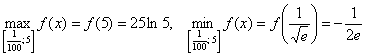
Дробно-рациональный экземпляр для самостоятельного решения:
Пример 6
Найти максимальное и минимальное значения функции на отрезке
![]()
Вычисления в данном случае не менее кропотливы и точно так же потребуют вмешательства калькулятора (если вы, конечно, не вундеркинд). Полное решение и ответ в конце урока.
Стрелки часов приближаются к 9 утра, и побережье потихоньку заполняется всё бОльшим и бОльшим количеством стройных ног. Если честно, не терпится захлопнуть ноут и похулиганить, но всё-таки мужественно разберу нетривиальную вещь:
Пример 7
Найти максимальное и минимальное значения функции на отрезке
![]()
Решение:
1) Найдём критические точки. Предварительно можно раскрыть скобки, но не особо сложнее использовать и правило дифференцирования произведения:
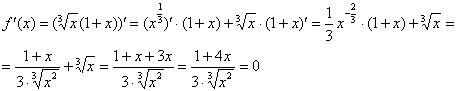
![]() – критические точки.
– критические точки.
Обратите внимание, что точка ![]() обращает знаменатель производной в ноль, но её следует отнести к критическим значениям, поскольку САМА ФУНКЦИЯ определена в данной точке. На этом случае я подробно останавливался в теоретической части и последнем примере урока Интервалы монотонностии и экстремумы функции.
обращает знаменатель производной в ноль, но её следует отнести к критическим значениям, поскольку САМА ФУНКЦИЯ определена в данной точке. На этом случае я подробно останавливался в теоретической части и последнем примере урока Интервалы монотонностии и экстремумы функции.
Кроме того, данная точка совпала с правым концом отрезка, а значит, в следующем пункте будет меньше расчётов. В следующем, но не сейчас:
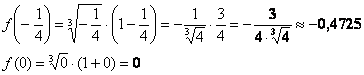
2) Вычислим значения функции на концах отрезка:
![]()
![]() уже известно.
уже известно.
Ответ: ![]()
Раз, два, три, четыре, пять – мне пора верстать.
Скорее всего, вы прочитали данную статью в ненастную погоду, поэтому желаю всем скорейшего летнего загара без зачётки в кармане! …Ну или с дипломом на груди… …Oй, что-то я не то сказал =)
Решения и ответы:
Пример 2. Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:
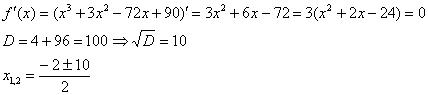
![]() – критические точки.
– критические точки.
![]()
2)Вычислим значения функции на концах отрезка:
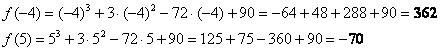
Ответ: ![]()
Пример 4. Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:
![]()
![]() – критические точки.
– критические точки.
![]()
2) Вычислим значения функции на концах отрезка:
![]() уже рассчитано в предыдущем пункте.
уже рассчитано в предыдущем пункте.
![]()
Ответ: ![]()
Пример 6. Решение:
1) Вычислим значения функции в критических точках, которые принадлежат данному отрезку:
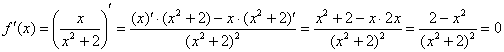
![]() – критические точки.
– критические точки.
![]()
2) Вычислим значения функции на концах отрезка:
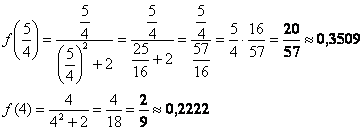
Ответ: 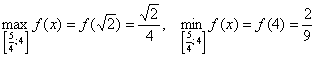
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright