


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Условные экстремумы и метод множителей Лагранжа
Сегодня на уроке мы научимся находить условные или, как их ещё называют, относительные экстремумы функций нескольких переменных, и, прежде всего, речь пойдёт, конечно же, об условных экстремумах функций двух и трёх переменных, которые встречаются в подавляющем большинстве тематических задач.
Что нужно знать и уметь на данный момент? Несмотря на то, что эта статья находится «на окраине» темы, для успешного усвоения материала потребуется не так уж и много. На данный момент вы должны ориентироваться в основных поверхностях пространства, уметь находить частные производные (хотя бы на среднем уровне) и, как подсказывает беспощадная логика, разбираться в безусловных экстремумах. Но даже если у вас низкий уровень подготовки, не спешите уходить – все недостающие знания/навыки реально «подобрать по пути», причём безо всяких многочасовых мучений.
Сначала проанализируем само понятие и заодно осуществим экспресс-повторение наиболее распространённых поверхностей. Итак, что же такое условный экстремум? …Логика здесь не менее беспощадна =) Условный экстремум функции – это экстремум в обычном понимании этого слова, который достигается при выполнении определённого условия (или условий).
Представьте произвольную «косую» плоскость в декартовой системе ![]() . Никакого экстремума здесь нет и в помине. Но это до поры до времени. Рассмотрим эллиптический цилиндр, для простоты – бесконечную круглую «трубу», параллельную оси
. Никакого экстремума здесь нет и в помине. Но это до поры до времени. Рассмотрим эллиптический цилиндр, для простоты – бесконечную круглую «трубу», параллельную оси ![]() . Очевидно, что эта «труба» «высечет» из нашей плоскости эллипс, в результате чего в верхней его точке будет максимум, а в нижней – минимум. Иными словами, функция, задающая плоскость, достигает экстремумов при условии, что её пересёк данный круговой цилиндр. Именно «при условии»! Другой эллиптический цилиндр, пересекающий эту плоскость, почти наверняка породит иные значения минимума и максимума.
. Очевидно, что эта «труба» «высечет» из нашей плоскости эллипс, в результате чего в верхней его точке будет максимум, а в нижней – минимум. Иными словами, функция, задающая плоскость, достигает экстремумов при условии, что её пересёк данный круговой цилиндр. Именно «при условии»! Другой эллиптический цилиндр, пересекающий эту плоскость, почти наверняка породит иные значения минимума и максимума.
Если не очень понятно, то ситуацию можно смоделировать реально (правда, в обратном порядке): возьмите топор, выйдите на улицу и срубите… нет, Гринпис потом не простит – лучше порежем «болгаркой» водосточную трубу =). Условный минимум и условный максимум будут зависеть от того, на какой высоте и под каким (негоризонтальным) углом осуществлён разрез.
Настало время облачить выкладки в математическое одеяние. Рассмотрим эллиптический параболоид ![]() , который имеет безусловный минимум в точке
, который имеет безусловный минимум в точке ![]() . Теперь найдём экстремум при условии
. Теперь найдём экстремум при условии ![]() . Данная плоскость параллельна оси
. Данная плоскость параллельна оси ![]() , а значит, «высекает» из параболоида параболу. Вершина этой параболы и будет условным минимумом. Причём плоскость
, а значит, «высекает» из параболоида параболу. Вершина этой параболы и будет условным минимумом. Причём плоскость ![]() не проходит через начало координат, следовательно, точка
не проходит через начало координат, следовательно, точка ![]() останется не при делах. Не представили картинку? Срочно идём по ссылкам! Потребуется ещё много-много раз.
останется не при делах. Не представили картинку? Срочно идём по ссылкам! Потребуется ещё много-много раз.
Вопрос: как найти этот условный экстремум? Простейший способ решения состоит в том, чтобы из уравнения ![]() (которое так и называют – условием или уравнением связи) выразить, например:
(которое так и называют – условием или уравнением связи) выразить, например: ![]() – и подставить его в функцию:
– и подставить его в функцию:
![]()
В результате получена функция одной переменной, задающая параболу, вершина которой «вычисляется» с закрытыми глазами. Найдём критические точки:
![]()
![]() – критическая точка.
– критическая точка.
Далее проще всего использовать второе достаточное условие экстремума:
![]()
В частности: ![]() , значит, функция достигает минимума в точке
, значит, функция достигает минимума в точке ![]() . Его можно вычислить напрямую:
. Его можно вычислить напрямую: ![]() , но мы пойдём более академичным путём. Найдём «игрековую» координату:
, но мы пойдём более академичным путём. Найдём «игрековую» координату:
![]() ,
,
запишем точку условного минимума ![]() , удостоверимся, что она действительно лежит в плоскости
, удостоверимся, что она действительно лежит в плоскости ![]() (удовлетворяет уравнению связи):
(удовлетворяет уравнению связи):
![]()
и вычислим условный минимум функции ![]() :
:
![]() при условии
при условии ![]() («добавка» обязательна!!!).
(«добавка» обязательна!!!).
Рассмотренный способ без тени сомнения можно использовать на практике, однако, он обладает рядом недостатков. Во-первых, далеко не всегда понятна геометрия задачи, а во-вторых, зачастую бывает невыгодно выражать «икс» либо «игрек» из уравнения связи (если вообще есть возможность что-то выразить). И сейчас мы рассмотрим универсальный метод нахождения условных экстремумов, получивший название метод множителей Лагранжа:
Пример 1
Найти условные экстремумы функции ![]() при указанном уравнении связи на аргументы
при указанном уравнении связи на аргументы ![]() .
.
![]()
Узнаёте поверхности? ;-) …Я рад видеть ваши счастливые лица =)
Кстати из формулировки данной задачи становится ясно, почему условие ![]() называют уравнением связи – аргументы функции
называют уравнением связи – аргументы функции ![]() связаны дополнительным условием, то есть найденные точки экстремума должны обязательно принадлежать круговому цилиндру.
связаны дополнительным условием, то есть найденные точки экстремума должны обязательно принадлежать круговому цилиндру.
Решение: на первом шаге нужно представить уравнение связи в виде ![]() и составить функцию Лагранжа:
и составить функцию Лагранжа:
![]() , где
, где ![]() – так называемый множитель Лагранжа.
– так называемый множитель Лагранжа.
В нашем случае ![]() и:
и:
![]()
Алгоритм нахождения условных экстремумов весьма похож на схему отыскания «обычных» экстремумов. Найдём частные производные функции Лагранжа, при этом с «лямбдой» следует обращаться, как с константой:
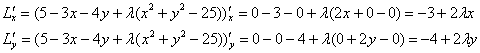
Составим и решим следующую систему:
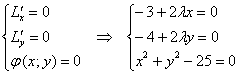
Клубок распутывается стандартно:
из первого уравнения выразим ![]() ;
;
из второго уравнения выразим ![]() .
.
Подставим ![]() в уравнение связи и проведём упрощения:
в уравнение связи и проведём упрощения:
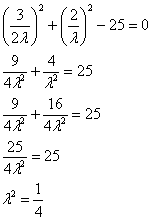
В результате получаем две стационарные точки. Если ![]() , то:
, то:
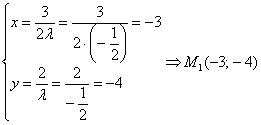
если ![]() , то:
, то:
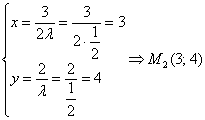
Легко видеть, что координаты обеих точек удовлетворяют уравнению ![]() . Щепетильные люди могут выполнить и полную проверку: для этого нужно подставить
. Щепетильные люди могут выполнить и полную проверку: для этого нужно подставить ![]() в первое
в первое ![]() и второе
и второе ![]() уравнения системы, и затем сделать то же самое с набором
уравнения системы, и затем сделать то же самое с набором ![]() . Всё должно «сойтись».
. Всё должно «сойтись».
Проверим выполнение достаточного условия экстремума для найденных стационарных точек. Я разберу три подхода к решению данного вопроса:
1) Первый способ – это геометрическое обоснование.
Вычислим значения функции ![]() в стационарных точках:
в стационарных точках:
![]()
Далее записываем фразу примерно такого содержания: сечение плоскости ![]() круговым цилиндром
круговым цилиндром ![]() представляет собой эллипс, в верхней вершине которого достигается максимум, а в нижней – минимум. Таким образом, бОльшее значение
представляет собой эллипс, в верхней вершине которого достигается максимум, а в нижней – минимум. Таким образом, бОльшее значение ![]() – есть условный максимум, а меньшее
– есть условный максимум, а меньшее ![]() – условный минимум.
– условный минимум.
По возможности лучше применять именно этот метод – он прост, и такое решение засчитывают преподаватели (большим плюсом идёт то, что вы показали понимание геометрического смысла задачи). Однако, как уже отмечалось, далеко не всегда понятно, что с чем и где пересекается, и тогда на помощь приходит аналитическая проверка:
2) Второй способ основан на использовании дифференциала второго порядка ![]() . Если окажется, что в стационарной точке
. Если окажется, что в стационарной точке ![]() , то функция достигает там максимума, если же
, то функция достигает там максимума, если же ![]() – то минимума.
– то минимума.
Найдём частные производные второго порядка:
![]()
и составим этот дифференциал:
![]()
При ![]() , значит, функция достигает максимума в точке
, значит, функция достигает максимума в точке ![]() ;
;
при ![]() , значит, функция достигает минимума в точке
, значит, функция достигает минимума в точке ![]() .
.
Следует отметить, что дифференциал ![]() представляет собой квадратичную форму относительно
представляет собой квадратичную форму относительно ![]() , и мы получаем быстрый результат, если эта форма определена отрицательно или положительно; причём она может быть таковой даже в «неочевидных» случаях наподобие
, и мы получаем быстрый результат, если эта форма определена отрицательно или положительно; причём она может быть таковой даже в «неочевидных» случаях наподобие ![]() – существует критерий Сильвестра, который позволяет легко установить положительность этого дифференциала.
– существует критерий Сильвестра, который позволяет легко установить положительность этого дифференциала.
Но что делать, когда форма знакопеременная, то есть когда знак ![]() зависит от значений
зависит от значений ![]() ? Например
? Например ![]() ?
?
В этом случае берём дифференциал от уравнения связи, проведём формальное решение для нашей задачи:
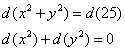
![]() , откуда выражаем, например,
, откуда выражаем, например, ![]() , и подставляем его в полный дифференциал
, и подставляем его в полный дифференциал ![]() :
:
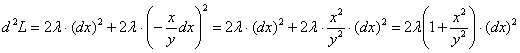 , после чего для
, после чего для ![]() и точки
и точки ![]() получаем:
получаем:
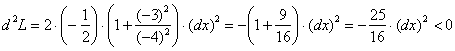 ;
;
и для ![]() :
:
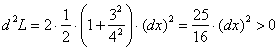
Гуд.
И, кроме того, можно использовать «тяжёлую артиллерию» – достаточное условие в матричной форме:
3) Продифференцируем по «икс» и по «игрек» уравнение связи:
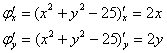
и составим следующую симметричную матрицу:
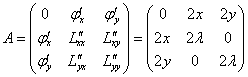
Если в стационарной точке ![]() , то функция достигает там (внимание!) минимума, если
, то функция достигает там (внимание!) минимума, если ![]() – то максимума.
– то максимума.
Запишем матрицу для значения ![]() и соответствующей точки
и соответствующей точки ![]() :
:
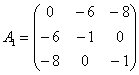
Вычислим её определитель:
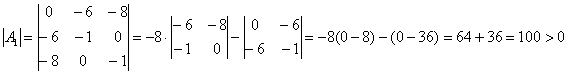 , таким образом, функция имеет максимум в точке
, таким образом, функция имеет максимум в точке ![]() .
.
Аналогично для значения ![]() и точки
и точки ![]() :
:
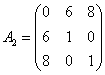
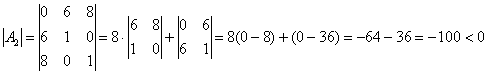 , таким образом, функция имеет минимум в точке
, таким образом, функция имеет минимум в точке ![]() .
.
Ответ: при условии ![]() :
:
![]()
После обстоятельного разбора материала просто не могу не предложить вам пару типовых задач для самопроверки:
Пример 2
Найти условный экстремум функции ![]() , если её аргументы связаны уравнением
, если её аргументы связаны уравнением ![]()
Пример 3
Найти экстремумы функции ![]() при условии
при условии ![]()
И вновь настоятельно рекомендую разобраться в геометрической сути заданий, особенно, это касается последнего примера, где аналитическая проверка достаточного условия – не подарок. Вспомните, какую линию 2-го порядка задаёт уравнение ![]() , и какую поверхность эта линия порождает в пространстве. Проанализируйте, по какой кривой цилиндр пересечёт плоскость и где на этой кривой будет минимум, а где – максимум.
, и какую поверхность эта линия порождает в пространстве. Проанализируйте, по какой кривой цилиндр пересечёт плоскость и где на этой кривой будет минимум, а где – максимум.
Решения и ответы в конце урока.
Рассматриваемая задача находит широкое применение в различных областях, в частности – далеко ходить не будем, в геометрии. Решим всем понравившуюся задачу о поллитровке (см. Пример 7 статьи Экстремальные задачи) вторым способом:
Пример 4
Каковы должны быть размеры консервной банки цилиндрической формы, чтобы на изготовления банки пошло наименьшее количество материала, если объем банки равен ![]()
Решение: рассмотрим переменный радиус основания ![]() , переменную высоту
, переменную высоту ![]() и составим функцию площади полной поверхности банки:
и составим функцию площади полной поверхности банки:
![]() (площадь двух крышек + площадь боковой поверхности)
(площадь двух крышек + площадь боковой поверхности)
Требуется найти минимум этой функции, при условии, что объём банки равен ![]() . Таким образом, функция Лагранжа получается прямо из словесной формулировки задачи!
. Таким образом, функция Лагранжа получается прямо из словесной формулировки задачи!
![]()
Найдём частные производные по «эр» и по «аш»:
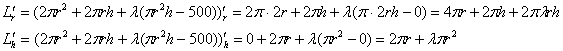
Составим и решим стандартную систему, при этом первое уравнение сразу сокращаем на ![]() , а второе – на «пи»:
, а второе – на «пи»:
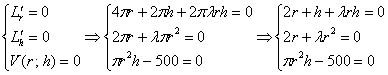
Удобнее начать со второго уравнения:
![]()
Нулевой радиус ![]() не удовлетворяет геометрическому смыслу задачи и поэтому для исследования остаётся 2-й множитель, из которого выражаем:
не удовлетворяет геометрическому смыслу задачи и поэтому для исследования остаётся 2-й множитель, из которого выражаем:
![]() – подставим в 1-е уравнение:
– подставим в 1-е уравнение:
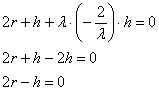
В результате получаем, что высота оптимальной банки должна быть в 2 раза больше радиуса основания:
![]()
Подставим ![]() в уравнение связи:
в уравнение связи:
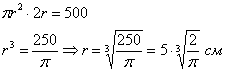
![]()
Осталась маленькая проблемка – проверить достаточное условие экстремума. А то вдруг в найденной точке 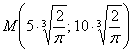 функция
функция ![]() наоборот – достигает максимального значения?
наоборот – достигает максимального значения?
Возможно, здесь существует лаконичное геометрическое обоснование, но с ходу мне его отыскать не удалось, и поэтому частные производные второго порядка:
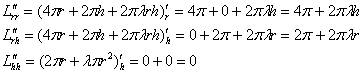
Составим полный дифференциал 2-го порядка:
![]()
Для нашей критической точки ![]() :
:
![]()
Легко убедиться, что данная квадратичная форма является знакопеременной, т.е. знак ![]() зависит от значений
зависит от значений ![]() и
и ![]() .
.
Поэтому находим дифференциал от уравнения связи. В соответствии с правилом дифференцирования произведения:
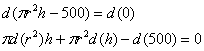
![]() , откуда выражаем
, откуда выражаем ![]() – и подставляем в полный дифференциал 2-го порядка:
– и подставляем в полный дифференциал 2-го порядка:
![]() , значит, функция площади
, значит, функция площади ![]() достигает минимума в точке
достигает минимума в точке 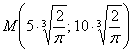 (при заданном объёме консервной банки).
(при заданном объёме консервной банки).
Желающие могут пойти более академичным путём, а именно, продифференцировать по «эр» и по «аш» уравнение связи:
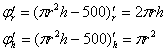
составить симметричную матрицу:
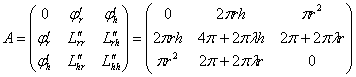
аккуратно подставить в неё ![]() и вычислить определитель
и вычислить определитель
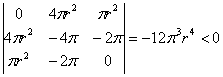 , с тем же самым выводом об условном минимуме в критической точке.
, с тем же самым выводом об условном минимуме в критической точке.
Если честно, хотел вообще опустить 3-й способ ввиду его трудоёмкости, но мало ли кому понадобится.
Ответ: радиус основания оптимальной банки: ![]() , её высота:
, её высота: ![]()
На практике выбор того или иного пути решения определяется темой, которую вы проходите, и сложностью выбранного метода. Кстати, первый способ (см. Пример 7 статьи Экстремальные задачи) с технической точки зрения ничуть не приятнее. Также следует отметить, что существует много задач, в которых без метода множителей Лагранжа уже не обойтись, и с таким геометрическим примером мы встретимся в следующем параграфе:
Условные экстремумы функции трёх переменных
Переключаем внимание на функцию трёх переменных ![]() , задачи с которой не менее популярны. Принципиальный алгоритм решения остаётся прежним:
, задачи с которой не менее популярны. Принципиальный алгоритм решения остаётся прежним:
Пример 5
Найти условный экстремум функции ![]() относительно уравнения связи
относительно уравнения связи ![]()
Решение: представим уравнение связи в виде ![]() и составим функцию Лагранжа:
и составим функцию Лагранжа:
![]()
Найдём частные производные 1-го порядка:
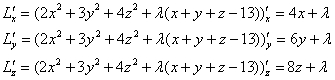
Приравниваем частные производные к нулю и присоединяем к системе уравнение связи:
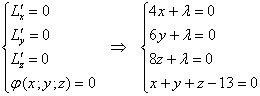
Из первых трёх уравнений выразим:
![]() – подставим в уравнение связи:
– подставим в уравнение связи:
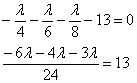
![]() – подставим в выражения для «икс», «игрек», «зет»:
– подставим в выражения для «икс», «игрек», «зет»:
![]()
Таким образом, стационарная точка: ![]()
Напоминаю, что в целях проверки будет не лишним подставить её координаты и значение ![]() во все уравнения системы. Здесь это легко сделать устно.
во все уравнения системы. Здесь это легко сделать устно.
Достаточное условие экстремума. С геометрией дела плохи и поэтому в нашем распоряжении остаются аналитические методы. Составим дифференциал второго порядка функции трёх переменных:
![]()
И перед нами не что иное, как квадратичная форма относительно ![]() .
.
Если в стационарной точке ![]() , то функция достигает в ней максимума, если
, то функция достигает в ней максимума, если ![]() – то минимума; если же
– то минимума; если же ![]() окажется знакопеременным, то потребуются дополнительные действия.
окажется знакопеременным, то потребуются дополнительные действия.
Найдём частные производные 2-го порядка:
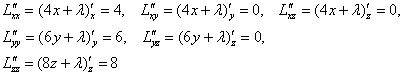
Надо сказать, большое везение чего я буду мучиться – даже подставлять ничего не пришлось:
![]() , значит, функция
, значит, функция ![]() достигает условного минимума в точке
достигает условного минимума в точке ![]() :
:
![]()
Ответ: при условии ![]() :
:
![]()
Тренируемся:
Пример 6
Найти условный экстремум функции ![]() относительно уравнения связи
относительно уравнения связи ![]()
Примерный образец чистового оформления задачи в конце урока.
Рассмотренные два примера – это самые что ни есть «заезженные» типовики, но время от времени встречаются и более трудные задания. Первая трудность, состоит, как правило, в решении системы, а вторая – в проверке достаточного условия экстремума. Приглашаю всех ознакомиться с заключительными примерами, которые не только интересны, но и требуют, я бы сказал, творческого подхода:
Пример 7
Найти экстремумы функции ![]() при условии
при условии ![]()
Казалось бы, ничто не предвещает сложностей, и решение начинается как обычно:
Запишем функцию Лагранжа ![]() и найдём её частные производные 1-го порядка:
и найдём её частные производные 1-го порядка:
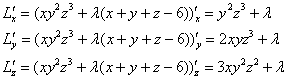
Составим стандартную систему:
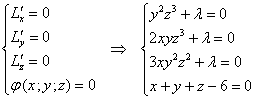
Привлекательнее всего выглядит 1-е уравнение, из которого, очевидно, рациональнее выразить «лямбду»:
![]() – подставим во второе уравнение:
– подставим во второе уравнение:
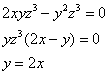
Примечание: если ![]() и / или
и / или ![]() , то
, то ![]() и уравнение связи фактически перестаёт играть таковую роль, поэтому данные случаи исключаем из рассмотрения.
и уравнение связи фактически перестаёт играть таковую роль, поэтому данные случаи исключаем из рассмотрения.
Теперь подставим ![]() в третье уравнение:
в третье уравнение:
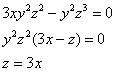
подставим ![]() в уравнение связи:
в уравнение связи:
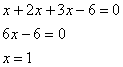
Таким образом: ![]()
На самом деле ещё не очень сложно, бывают куда более «плохие» системы.
Теперь найдём частные производные 2-го порядка:
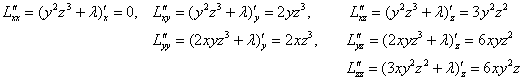
и аккуратно, ВНИМАТЕЛЬНО составим соответствующий полный дифференциал:
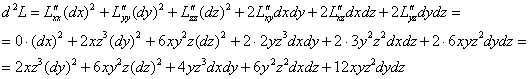
Вычислим значение дифференциала в точке ![]() :
:
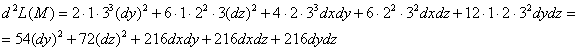
Используя критерий Сильвестра (да и просто анализируя слагаемые), легко убедиться, что данная квадратичная форма знакопеременна, т.е. знак ![]() зависит от значений
зависит от значений ![]() . Поэтому используем уже знакомую схему действий. Найдём дифференциал от уравнения связи, здесь он элементарен:
. Поэтому используем уже знакомую схему действий. Найдём дифференциал от уравнения связи, здесь он элементарен:
![]()
Теперь нужно выразить какой-нибудь дифференциал, в нашем случае выгоднее ![]() – подставляем его в наше «знакопеременное недоразумение»:
– подставляем его в наше «знакопеременное недоразумение»:
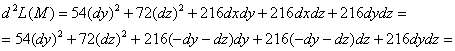
после чего раскрываем скобки и приводим подобные слагаемые:
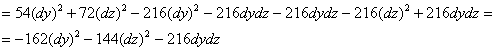
В результате получена квадратичная форма уже от двух переменных, запишем её матрицу:
![]()
и вычислим угловые миноры:
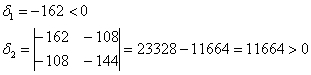
Таким образом, квадратичная форма определена отрицательно:
![]() , а значит, функция
, а значит, функция ![]() достигает условного максимума в точке
достигает условного максимума в точке ![]() :
:
![]()
Есть ли другой способ проверки достаточного условия? Есть.
Составляем симметрическую матрицу:
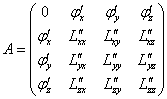
где, ![]() – частные производные уравнения связи.
– частные производные уравнения связи.
Далее рассчитываем угловые миноры 3-го и 4-го порядка в стационарной точке:
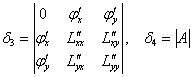
Если окажется, что ![]() , то функция
, то функция ![]() достигает условного минимума в стационарной точке; если
достигает условного минимума в стационарной точке; если ![]() – то условного максимума.
– то условного максимума.
В нашей задаче: ![]() ,
,
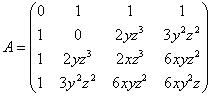
и для точки ![]() получаем следующую матрицу:
получаем следующую матрицу:

Желающие могут провести вычисления, найти ![]() (рациональнее именно в таком порядке) и сделать тот же самый вывод о наличии условного максимума.
(рациональнее именно в таком порядке) и сделать тот же самый вывод о наличии условного максимума.
Разумеется, матричный способ более громоздкий, но возможно, кому-то придётся по вкусу.
Ответ: при условии ![]() :
:
![]()
Интересно отметить, что в рассмотренном примере нам даже не потребовалось находить значение «лямбда».
Обещанная геометрическая задача:
Пример 8
Определите размеры прямоугольного параллелепипеда (длину, ширину, высоту) максимального объема, если известно, что сумма длин всех его рёбер равна ![]() .
.
Постарайтесь не только найти решение, но и добросовестно проверить достаточное условие экстремума.
До сих пор нам встречались задания с единственным уравнением связи, но, вообще говоря, условий может быть несколько: два, три и бОльшее количество. И иногда такие примеры не только существуют в «чистой теории», но и реально встречаются на практике:
Пример 9
Исследовать на экстремум функции ![]() при условиях
при условиях ![]()
Здесь функция Лагранжа принимает вид ![]() и дальнейшие действия будут отличаться мало: находим частные производные 1-го порядка и приравниваем их к нулю, при этом к системе нужно присоединить оба уравнения связи. После нахождения стационарной точки проверяем достаточное условие экстремума, для которого «хватает» дифференциала 2-го порядка.
и дальнейшие действия будут отличаться мало: находим частные производные 1-го порядка и приравниваем их к нулю, при этом к системе нужно присоединить оба уравнения связи. После нахождения стационарной точки проверяем достаточное условие экстремума, для которого «хватает» дифференциала 2-го порядка.
Решите этот пример самостоятельно – и вы очень удивитесь, как всё легко!
Задача отыскания условных экстремумов реализуема и для функций бОльшего числа переменных, причём условий может быть тоже сколько угодно. Общий алгоритм, думаю, понятен: находим частные производные по всем переменным, приравниваем их к нулю и добавляем в систему все уравнения связи. При проверке достаточного условия экстремума выгоднее использовать теорию квадратичных форм, при необходимости уменьшая количество входящих в неё переменных (отыскивая и выражая дифференциалы из уравнений связи). Однако существует и общая матричная форма достаточного условия, частные случаи которой мы тоже разобрали.
Надеюсь, вы отлично провели время! ...правда, не очень хорошо, что я научил вас спиливать водосточные трубы =) …но зато вдруг стало понятно, почему в стране разруха…. Потому что испокон веков на Руси были такие учителя!
Жду от вас свежих идей =)
Решения и ответы:
Пример 2: Решение: из уравнения связи выразим ![]() – подставим в функцию:
– подставим в функцию:
![]()
Найдём критические точки:
![]()
![]() – критическая точка.
– критическая точка.
Проверим выполнение достаточного условия экстремума:
![]()
В частности: ![]() , значит, функция достигает максимума в точке
, значит, функция достигает максимума в точке ![]() .
.
![]()
![]() – точка условного максимума.
– точка условного максимума.
![]()
Ответ: при условии ![]() :
:
![]()
Пример 3: Решение: составим функцию Лагранжа:
![]()
и найдём её частные производные 1-го порядка:
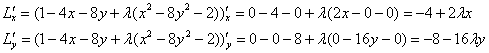
Найдём критические точки:
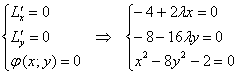
Из 1-го уравнения: ![]()
Из 2-го уравнения: ![]()
Подставим ![]() в уравнение связи:
в уравнение связи:
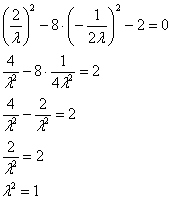
Если ![]() , то
, то ![]()
Если ![]() , то
, то ![]()
Проверим выполнение достаточного условия экстремума.
Способ первый: гиперболический цилиндр ![]() , параллельный оси
, параллельный оси ![]() , пересекает плоскость
, пересекает плоскость ![]() по гиперболе. Вершина нижней ветви этой гиперболы будет максимумом, а вершина верхней ветви – минимумом. Вычислим значения функции в стационарных точках:
по гиперболе. Вершина нижней ветви этой гиперболы будет максимумом, а вершина верхней ветви – минимумом. Вычислим значения функции в стационарных точках:
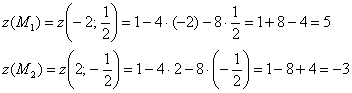
Поскольку ![]() , то
, то ![]() – условный максимум, а
– условный максимум, а ![]() – условный минимум.
– условный минимум.
Способ второй: найдём частные производные второго порядка:
![]()
и составим соответствующий дифференциал:
![]()
Полученная квадратичная форма является знакопеременной (знак ![]() зависит от значений
зависит от значений ![]() ), поэтому найдём дифференциал от уравнения связи:
), поэтому найдём дифференциал от уравнения связи:
![]()
![]() , откуда выразим
, откуда выразим ![]() и подставим в полный дифференциал 2-го порядка:
и подставим в полный дифференциал 2-го порядка:
![]() .
.
Для ![]() :
:
![]() , значит, функция достигает условного минимума в точке
, значит, функция достигает условного минимума в точке ![]() .
.
Для ![]() :
:
![]() , значит, функция достигает условного максимума в точке
, значит, функция достигает условного максимума в точке ![]() .
.
Способ третий: продифференцируем уравнение связи:
![]()
и составим следующую матрицу:
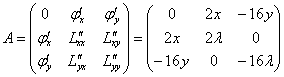
Запишем матрицу для значения ![]() и точки
и точки ![]() :
:
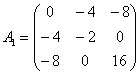
и вычислим её определитель:
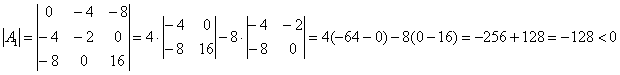 , таким образом, функция имеет минимум в точке
, таким образом, функция имеет минимум в точке ![]() .
.
Запишем матрицу для ![]() , точки
, точки ![]() :
:
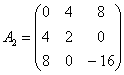
и вычислим её определитель:
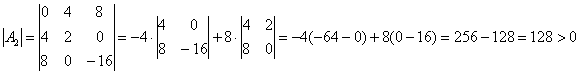 , таким образом, функция имеет максимум в точке
, таким образом, функция имеет максимум в точке ![]() .
.
Ответ: при условии ![]() :
:
![]()
Пример 6: Решение: составим функцию Лагранжа:
![]()
Найдём частные производные 1-го порядка:
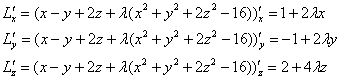
Найдём стационарные точки:
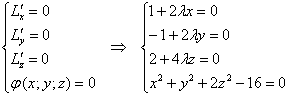
Из первых трёх уравнений выразим:
![]() – подставим в уравнение связи:
– подставим в уравнение связи:
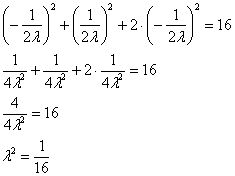
Если ![]() , то
, то 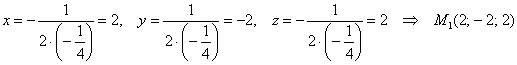
Если ![]() , то
, то 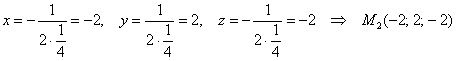
Проверим выполнение достаточного условия экстремума. Составим дифференциал второго порядка:
![]()
Найдём частные производные второго порядка:
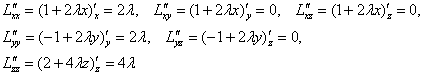
Таким образом: ![]()
При ![]() , значит, функция
, значит, функция ![]() достигает условного максимума в точке
достигает условного максимума в точке ![]() .
.
При ![]() , значит, функция
, значит, функция ![]() достигает условного минимума в точке
достигает условного минимума в точке ![]() .
.
Ответ: при условии ![]() :
:
![]()
Пример 8: Решение: обозначим через ![]() – длину, ширину и высоту прямоугольного параллелепипеда. По условию:
– длину, ширину и высоту прямоугольного параллелепипеда. По условию: ![]() . При данном условии требуется найти максимальное значение объёма
. При данном условии требуется найти максимальное значение объёма ![]() параллелепипеда.
параллелепипеда.
Составим функцию Лагранжа ![]() и найдём её частные производные:
и найдём её частные производные:
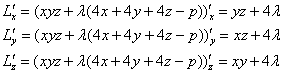
Найдём стационарные точки:
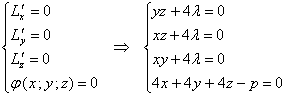
Из первых трёх уравнений следуют соотношения:
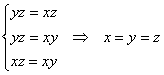
Таким образом:
![]()
![]() – стационарная точка.
– стационарная точка.
Проверим выполнение достаточного условия экстремума. Найдём частные производные 2 порядка
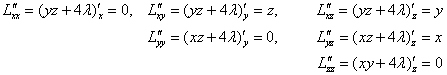
и составим соответствующий полный дифференциал:
![]()
Для точки ![]() :
:
![]()
Очевидно, что данная квадратичная форма знакопеременна. Найдём дифференциал от уравнения связи:
![]()
![]() , откуда выразим, например,
, откуда выразим, например, ![]() – подставим в полный дифференциал 2 порядка и проведём упрощения:
– подставим в полный дифференциал 2 порядка и проведём упрощения:
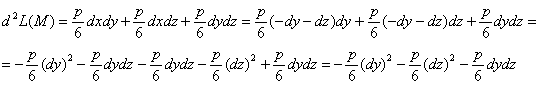
В результате получена квадратичная форма уже двух переменных, запишем её матрицу:
![]()
и вычислим угловые миноры:
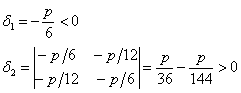
Согласно критерию Сильвестра, ![]() , значит, функция
, значит, функция ![]() достигает усл. максимума в точке
достигает усл. максимума в точке ![]() :
:
![]()
Ответ: оптимальный параллелепипед представляет собой куб с ребром ![]() , при этом максимальный объём:
, при этом максимальный объём: ![]()
Пример 9: Решение: из 1-го уравнения связи выразим ![]() – подставим во 2-е уравнение связи:
– подставим во 2-е уравнение связи:
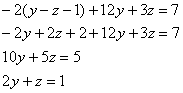
![]() – подставим в выражение
– подставим в выражение ![]() :
:
![]()
Подставим ![]() и
и ![]() в функцию:
в функцию:
![]()
Найдём критические точки:
![]()
![]()
Проверим выполнение достаточного условия экстремума:
![]() , в частности:
, в частности:
![]() , значит, функция достигает минимума в точке
, значит, функция достигает минимума в точке ![]()
Вычислим две другие координаты:
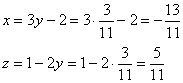
![]() – точка условного минимума функции
– точка условного минимума функции ![]() .
.
![]()
Ответ: при условиях ![]() :
:
![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright