


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
23. Нелинейная регрессия. Виды и примеры решений
На предыдущем уроке мы рассмотрели общую модель однофакторной регрессии, а также изучили линейный случай. Но им, разумеется, кухня не ограничивается, а посему тема получает логичное продолжение. Прямо сейчас вы узнаете, как подобрать вид регрессии, и, конечно же, отведаете основные блюда:
Экспоненциальная регрессия (наиболее подробно, рекомендую всем)
Гиперболическая регрессия
СтепеннАя регрессия
Параболическая регрессия
Логарифмическая регрессия
Все регрессии строятся по одному шаблону, и мы начинаем:
Пример 74
В результате наблюдения за размножением бактерий были получены следующие результаты:
![]()
где, ![]() – время (часы), а
– время (часы), а ![]() – количество бактерий …Время обычно обозначают буквой «тэ», но для единообразия пусть будет старый добрый «икс».
– количество бактерий …Время обычно обозначают буквой «тэ», но для единообразия пусть будет старый добрый «икс».
Требуется:
1) построить диаграмму рассеяния и подобрать линию, которая эффективно приближает эмпирические данные;
2) методом наименьших квадратов найти уравнение регрессии ![]() на
на ![]() , выполнить чертёж;
, выполнить чертёж;
3) вычислить индекс детерминации и индекс корреляции;
4) проверить значимость полученной модели на уровне значимости ![]() ;
;
5) найти среднюю ошибку аппроксимации;
6) оценить количество бактерий к 12-му и 24-му часу.
По каждому пункту сделать выводы.
Решение:
1) В Примере 73 мы не только построили диаграмму рассеяния по предложенным числовым данным, но и выполнили почти все пункты задания для линейного случая:
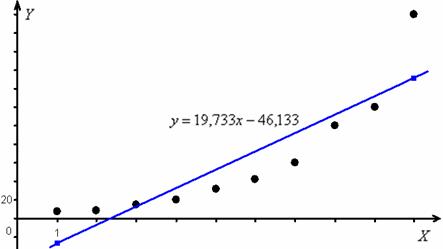
И невооруженным взглядом видно, что линейная регрессия неудовлетворительно аппроксимирует (приближает) опытные данные. Сразу бросается в глаза, что эмпирические точки имеют тенденцию располагаться по кривой, и во-вторых, количество бактерий не может быть отрицательным, но по уравнению ![]() – запросто так может.
– запросто так может.
Таким образом, задача состоит в том, чтобы подобрать линию (её тип), которая удачно приблизит эмпирические точки. Возможно, не наилучшим образом, но, по крайне мере, хорошо. Выбор подходящей линии и соответствующей записи уравнения регрессии называют спецификацией модели.
Этот вопрос можно решить, исходя из содержательного условия задачи, и, естественно, математически. Так, размножение бактерий, насекомых, появление новых частиц в результате физической или химической реакции обычно носит экспоненциальный характер. То есть растёт по экспоненте ![]() , где
, где![]() и
и ![]() – некоторые константы. С увеличением значений «икс» наблюдается стремительный, прямо-таки «взрывной» рост «игреков», и наши опытные данные (см. рис. выше) как раз напоминают эту ситуацию.
– некоторые константы. С увеличением значений «икс» наблюдается стремительный, прямо-таки «взрывной» рост «игреков», и наши опытные данные (см. рис. выше) как раз напоминают эту ситуацию.
С другой стороны, подходящий тип линии выявляют прямым перебором основных графиков – методом наименьших квадратов строят оптимальную прямую, параболу, гиперболу, экспоненту и т. д., и анализируют, какая функция лучше приближает эмпирические точки. Качество приближения оценивают с помощью индекса детерминации ![]() (чем больше к единице, тем лучше) и средней ошибки аппроксимации
(чем больше к единице, тем лучше) и средней ошибки аппроксимации ![]() (чем ближе к нулю, тем лучше). Но это, конечно, большой объём работы, который лучше поручить статистическим программам. Простейший перебор можно выполнить в обычном Экселе, и я даже записал небольшой ролик на эту тему (смотреть до конца!!):
(чем ближе к нулю, тем лучше). Но это, конечно, большой объём работы, который лучше поручить статистическим программам. Простейший перебор можно выполнить в обычном Экселе, и я даже записал небольшой ролик на эту тему (смотреть до конца!!):
 Если видео недоступно, то есть копия на Рутубе
Если видео недоступно, то есть копия на Рутубе
Итак, в нашей задаче наилучшим выбором действительно является экспонента ![]() , а конкретно
, а конкретно ![]() . Но то было программное решение с готовым результатом, а нам-то нужно всё рассчитать подробно, чем мы сейчас и займёмся:
. Но то было программное решение с готовым результатом, а нам-то нужно всё рассчитать подробно, чем мы сейчас и займёмся:
2) Методом наименьших квадратов найдём уравнение нелинейной, в данном случае экспоненциальной регрессии ![]() .
.
Коэффициенты ![]() и
и ![]() определим из решения системы:
определим из решения системы:
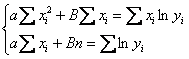 , где
, где ![]()
Откуда и из каких соображений взялась эта система, можно узнать в статье Метод наименьших квадратов, ну а мы займёмся её эксплуатацией. Заполним расчётную таблицу (в нижней строке – суммы по столбцам):
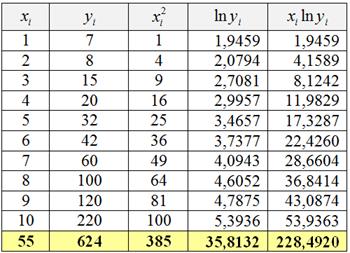
Неоднократно повторял, но ещё раз – подобные расчёты легко и быстро выполняются в MS Excel, смотрИте, например, этот ролик. Для вычисления натурального логарифма используем стандартную функцию =LN( ).
! Примечание: суммы в последних двух столбцах выглядят округлёнными, но Эксель рассчитывает их более точно, поэтому в последующих вычислениях формально будут некоторые погрешности. Кроме того, довольно часто я буду пренебрегать значком ![]() , записывая строгое равенство.
, записывая строгое равенство.
Таким образом, получаем систему:
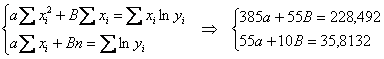
Систему решим по формулам Крамера. Вычислим главный определитель:
![]() , значит, система имеет единственное решение.
, значит, система имеет единственное решение.
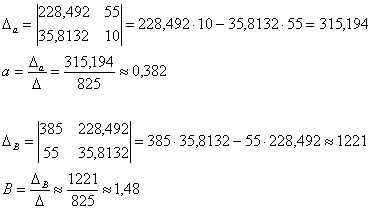
и не забываем выразить непосредственно коэффициент ![]()
В результате, искомая экспонента: ![]() . Напоминаю, что полученное уравнение наилучшим образом приближает эмпирические точки по сравнению с любой другой экспонентой из семейства
. Напоминаю, что полученное уравнение наилучшим образом приближает эмпирические точки по сравнению с любой другой экспонентой из семейства ![]() . Выполним чертёж:
. Выполним чертёж:
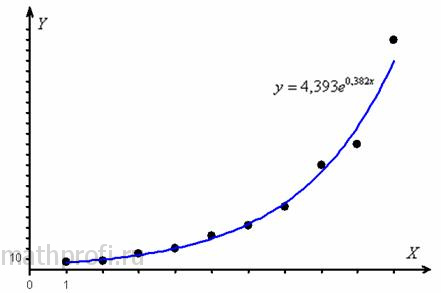
Если выполняете его от руки, то для построения экспоненты можно использовать опорные значения ![]() , вычисленные в таблице ниже.
, вычисленные в таблице ниже.
3) Найдём индекс детерминации и индекс корреляции. Для этого вычислим среднее значение признака-результата ![]() и заполним расчётную таблицу, сразу с добавочным столбцом для расчёта СОА в пункте 5:
и заполним расчётную таблицу, сразу с добавочным столбцом для расчёта СОА в пункте 5:
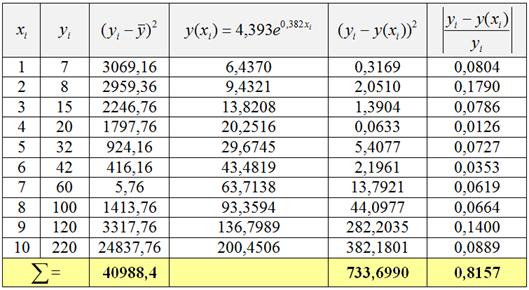
В результате, общая сумма квадратов ![]() , остаточная сумма квадратов
, остаточная сумма квадратов ![]() и индекс детерминации:
и индекс детерминации:
![]() – таким образом, в рамках построенной модели размножение бактерий (результат
– таким образом, в рамках построенной модели размножение бактерий (результат ![]() ) на 98,21% объяснено течением времени (фактором
) на 98,21% объяснено течением времени (фактором ![]() ). Остальные 1,79% вариации признака-результата обусловлены другими, не учтёнными в модели факторами.
). Остальные 1,79% вариации признака-результата обусловлены другими, не учтёнными в модели факторами.
Вычислим индекс корреляции:
![]() – таким образом, согласно шкале Чеддока, существует практически функциональная зависимость признака-результата
– таким образом, согласно шкале Чеддока, существует практически функциональная зависимость признака-результата ![]() от фактора
от фактора ![]() .
.
4) Проверим статистическую значимость построенной модели. Говоря простыми словами, нужно выяснить – а можно ли доверять полученным выборочным результатам? Или же они случайны? (по той причине, что выборка малА). Ответ на этот вопрос тут очевиден, но нужно оформить формальное решение.
На уровне значимости ![]() проверим нулевую гипотезу
проверим нулевую гипотезу ![]() – о том, что генеральный индекс детерминации равен нулю, против конкурирующей гипотезы:
– о том, что генеральный индекс детерминации равен нулю, против конкурирующей гипотезы: ![]() .
.
Используем статистический критерий 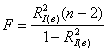 , где
, где ![]() – значение выборочного индекса детерминации. В разных выборках оно будет разным, а посему
– значение выборочного индекса детерминации. В разных выборках оно будет разным, а посему ![]() – есть величина случайная (как и любой другой статистический критерий).
– есть величина случайная (как и любой другой статистический критерий).
Для уровня значимости ![]() и количества степеней свободы
и количества степеней свободы ![]() по соответствующей таблице или с помощью Расчётного макета (пункт 12) определяем критическое значение критерия:
по соответствующей таблице или с помощью Расчётного макета (пункт 12) определяем критическое значение критерия: ![]()
Вычислим наблюдаемое значение критерия: ![]() – оно попало, да ещё как, в критическую область
– оно попало, да ещё как, в критическую область ![]() :
:

– поэтому на уровне значимости ![]() гипотезу
гипотезу ![]() отвергаем в пользу гипотезы
отвергаем в пользу гипотезы ![]() .
.
Вывод: полученный результат ![]() статистически значим, следовательно, статистически значимо и выборочное уравнение
статистически значим, следовательно, статистически значимо и выборочное уравнение ![]() экспоненциальной регрессии. То есть, с точки зрения статистики, получилось не фуфло.
экспоненциальной регрессии. То есть, с точки зрения статистики, получилось не фуфло.
…Да, если вам не очень понятны эти танцы с бубном, то ознакомьтесь с общей моделью регрессии и линейным случаем в частности, где я рассказал, что к чему.
5) Вычислим среднюю ошибку аппроксимации:
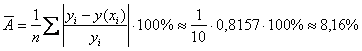 – таким образом, регрессионные значения
– таким образом, регрессионные значения ![]() отличаются от соответствующих эмпирических значений
отличаются от соответствующих эмпирических значений ![]() в среднем на 8,16%, что можно признать хорошим результатом.
в среднем на 8,16%, что можно признать хорошим результатом.
6) Спрогнозируем количество бактерий к 12-му и 24-му часу:
![]() бактерий;
бактерий;
![]() бактерий.
бактерий.
Вот такой вот он, экспоненциальный рост. Но это не беда. Domestos, миллионы микробов умрут (с).
Аналогичное задание для самостоятельного решения:
Пример 75
В результате исследования получены следующие данные:
![]()
где, ![]() – количество выпущенной продукции (тысяч единиц), а
– количество выпущенной продукции (тысяч единиц), а ![]() – себестоимость одной единицы продукции (руб.)
– себестоимость одной единицы продукции (руб.)
1) Методом наименьших квадратов найти уравнение ![]() гиперболической регрессии, выполнить чертёж.
гиперболической регрессии, выполнить чертёж.
2) Вычислить индекс детерминации и корреляции.
3) Проверить значимость полученной модели на уровне ![]() .
.
4) Найти среднюю ошибку аппроксимации.
По каждому пункту сделать выводы.
Система – вот:

а числа уже в Экселе – не ленимся провести вычисления! Ничего страшного, если получится не сильно красиво, важно отработать сам алгоритм.
Обратите внимание, что в этой задаче сразу предложен вид регрессии, и это не случайность. Гиперболическая зависимость характерна для процессов, где есть некий предел («насыщение») – когда дальнейшее увеличение (либо уменьшение) факторной переменной практически перестаёт оказывать влияние на результат (ещё раз проанализируйте числа в таблице выше). Яркий пример есть в физике – это остывание кипятка: наиболее сильно температура падает в первый час, в течение же последующих часов она уменьшается уже незначительно. И пример с ростом: мышечная масса человека будет заметно расти с увеличением физических нагрузок, но настанет такой момент, когда этот рост практически прекратится, как ни увеличивай интенсивность и продолжительность тренировок. И здесь остаётся только «химия», к которой прибегают практически все культуристы (ни в коем случае не призыв).
Рассмотрим ещё одну регрессию и ещё одну классическую задачу, снова из экономики:
Пример 76
По результатам 12 лет имеются следующие данные:
![]()
где, ![]() – средняя цена товара по торговым точкам региона (ден. ед.), а
– средняя цена товара по торговым точкам региона (ден. ед.), а ![]() – общее количество проданных за год товаров (тыс. штук).
– общее количество проданных за год товаров (тыс. штук).
Требуется:
1) Методом наименьших квадратов найти функцию спроса ![]() , выполнить чертёж.
, выполнить чертёж.
2) Вычислить индексы детерминации и корреляции и проверить значимость построенной модели на уровне ![]() .
.
3) Вычислить среднюю ошибку аппроксимации.
+ Новинка:
4) Определить коэффициент эластичности спроса.
И само собой, выводы, выводы, выводы. Выводы.
Но перед тем как оформлять решение, немного порассуждаем: что происходит, когда повышается цена на какой-то товар? Это зависит от того, что это за товар и ещё от некоторых факторов. Но чаще спрос (количество проданных товаров) падает, причём, падать он может разными темпами. Приступаем:
1) Составим уравнение регрессионной зависимости спроса ![]() от цены товара. Почему именно степеннАя регрессия во многих случаях удачно моделирует спрос, мы разберёмся чуть позже, после освоения технической стороны вопроса. Заполним расчётную таблицу:
от цены товара. Почему именно степеннАя регрессия во многих случаях удачно моделирует спрос, мы разберёмся чуть позже, после освоения технической стороны вопроса. Заполним расчётную таблицу:
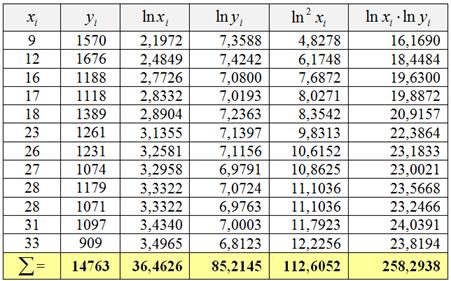
Напоминаю, что в Экселе есть функция =LN( ), и обратите внимание на магию логарифмов – как они уменьшили «иксовые» и особенно «игрековые» значения.
Коэффициенты регрессии ![]() найдём из решения системы:
найдём из решения системы:
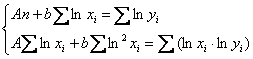 , где
, где ![]() .
.
В нашем случае объём совокупности ![]() и:
и:
![]()
Систему решим по формулам Крамера,… а, кстати, почему всё время Крамер да Крамер? С десятичными хвостатыми дробями это наиболее удобный способ:
![]() , значит, система имеет единственное решение.
, значит, система имеет единственное решение.

после чего находим сам коэффициент: ![]() .
.
И коэффициент «бэ»:

Таким образом, ![]() – степеннАя регрессионная зависимость количества проданных товаров от цены. Изобразим на чертеже эмпирические точки и график регрессии:
– степеннАя регрессионная зависимость количества проданных товаров от цены. Изобразим на чертеже эмпирические точки и график регрессии:
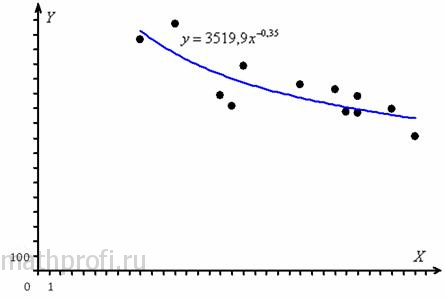
Что можно сказать «по первой оглядке»? При увеличении цены спрос сначала припал, а затем уже не очень-то хочет снижаться. Подумайте, что это может быть за товар. Также обращаю внимание на схожесть с гиперболической регрессией, и это неудивительно, ведь график ![]() при
при ![]() представляет собой кривую гиперболического типа, а при
представляет собой кривую гиперболического типа, а при ![]() мы собственно и получаем обычную «школьную» гиперболу.
мы собственно и получаем обычную «школьную» гиперболу.
2) Вычислим индексы детерминации и корреляции. Для этого найдём среднее значение признака-результата ![]() и заполним ещё одну расчётную таблицу:
и заполним ещё одну расчётную таблицу:
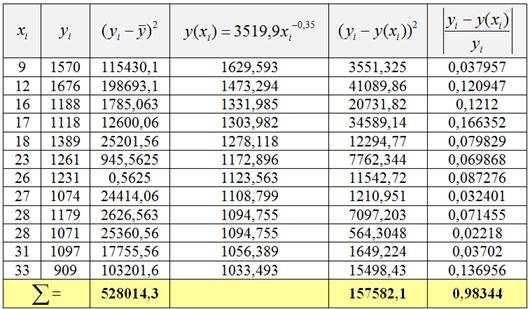
В результате, общая сумма квадратов ![]() , остаточная сумма квадратов
, остаточная сумма квадратов ![]() и индекс детерминации:
и индекс детерминации:
![]() – таким образом, в рамках построенной модели спрос на 70,16% зависит от изменения цены, а оставшаяся часть вариации (29,84%) спроса обусловлена факторами, не учтёнными моделью.
– таким образом, в рамках построенной модели спрос на 70,16% зависит от изменения цены, а оставшаяся часть вариации (29,84%) спроса обусловлена факторами, не учтёнными моделью.
Вычислим индекс корреляции:
![]() – таким образом, существует сильная корреляционная зависимость количества проданных товаров от цены.
– таким образом, существует сильная корреляционная зависимость количества проданных товаров от цены.
На уровне значимости ![]() проверим нулевую гипотезу
проверим нулевую гипотезу ![]() (генеральный индекс детерминации равен нулю), против конкурирующей гипотезы
(генеральный индекс детерминации равен нулю), против конкурирующей гипотезы ![]() . Используем статистический критерий
. Используем статистический критерий 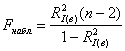 , где
, где ![]() – значение выборочного индекса детерминации.
– значение выборочного индекса детерминации.
Для ![]() и количества степеней свободы
и количества степеней свободы ![]() по соответствующей таблице или с помощью Расчётного макета (пункт 12) определим критическое значение критерия:
по соответствующей таблице или с помощью Расчётного макета (пункт 12) определим критическое значение критерия: ![]()
Наблюдаемое значение критерия: ![]() – попало в критическую область:
– попало в критическую область:

поэтому на уровне значимости ![]() гипотезу
гипотезу ![]() отвергаем в пользу гипотезы
отвергаем в пользу гипотезы ![]() .
.
Вывод: выборочное значение ![]() статистически значимо, следовательно, статистически значимо и выборочное уравнение
статистически значимо, следовательно, статистически значимо и выборочное уравнение ![]() степеннОй регрессии.
степеннОй регрессии.
3) Вычислим среднюю ошибку аппроксимации:
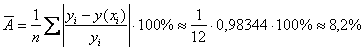 – таким образом, регрессионные значения
– таким образом, регрессионные значения ![]() отличаются от соответствующих эмпирических значений
отличаются от соответствующих эмпирических значений ![]() в среднем на 8,2%, что является хорошим результатом.
в среднем на 8,2%, что является хорошим результатом.
4) Определим коэффициент эластичности ![]() («эпсилон»).
(«эпсилон»).
Этот коэффициент показывает, на сколько процентов изменится значение признака результата ![]() при увеличении признака-фактора
при увеличении признака-фактора ![]() на 1%. В случае степеннОй регрессии
на 1%. В случае степеннОй регрессии ![]() коэффициент эластичности
коэффициент эластичности ![]() – постоянен и в точности равен параметру «бэ».
– постоянен и в точности равен параметру «бэ».
В нашей задаче ![]() и
и ![]() – таким образом, при увеличении цены (значения «икс») на один процент – спрос на товар (значение «игрек») уменьшается примерно на 0,35%. Таким образом, спрос падает медленнее, чем растёт цена. Математически этот факт можно записать так:
– таким образом, при увеличении цены (значения «икс») на один процент – спрос на товар (значение «игрек») уменьшается примерно на 0,35%. Таким образом, спрос падает медленнее, чем растёт цена. Математически этот факт можно записать так: ![]() – и это означает, что такой товар неэластичен по спросу. Как правило, это вещи первой необходимости и / или товары, которые трудно заменить – соль, хлеб, некоторые лекарства, бензин, лампочки, патроны и т. п. Так, если хлеб подорожает в два раза, то спрос несколько снизится, но существенно не упадёт. Цена и объём продаж, к слову, в нашей задаче смахивают именно на хлеб.
– и это означает, что такой товар неэластичен по спросу. Как правило, это вещи первой необходимости и / или товары, которые трудно заменить – соль, хлеб, некоторые лекарства, бензин, лампочки, патроны и т. п. Так, если хлеб подорожает в два раза, то спрос несколько снизится, но существенно не упадёт. Цена и объём продаж, к слову, в нашей задаче смахивают именно на хлеб.
Если ![]() , то спрос падает быстрее, нежели растёт цена. Такой товар называют эластичным по спросу. Это значит, что его легко заменить или вообще отказаться от покупки. Так, если сильно подорожает мясо, то спрос на него резко упадёт – большинство людей «безболезненно» перейдут на курицу и рыбу. Некоторые станут веганами :) Ну а если в два раза подорожает золото, то большинство ювелирных магазинов просто закроется (в отличие от хлебных).
, то спрос падает быстрее, нежели растёт цена. Такой товар называют эластичным по спросу. Это значит, что его легко заменить или вообще отказаться от покупки. Так, если сильно подорожает мясо, то спрос на него резко упадёт – большинство людей «безболезненно» перейдут на курицу и рыбу. Некоторые станут веганами :) Ну а если в два раза подорожает золото, то большинство ювелирных магазинов просто закроется (в отличие от хлебных).
Понятие эластичности, естественно, относится не только к спросу, а формально вообще к любому фактору и результату, и чёткое определение эластичности дано в начале этого пункта. Он (коэффициент) может и не иметь содержательного смысла – это зависит от условия той или иной задачи.
Коэффициент эластичности можно рассчитать и для других видов регрессии – по специальной формуле, которую я привёл в статье Линейный коэффициент корреляции. Но там мы вычислили средний коэффициент эластичности, ибо почти во всех случаях эластичность зависит от значения «икс». И только степеннАя регрессия ![]() обладает тем замечательным свойством, что эластичность
обладает тем замечательным свойством, что эластичность ![]() – есть константа для любого допустимого «икс».
– есть константа для любого допустимого «икс».
И гвоздь программы! – для любителей хардкора. Завершим урок параболической регрессией:
Пример 77
По результатам выборочного исследования 10 хозяйств области получены следующие данные:
![]()
где, ![]() – количество внесённых минеральных удобрений на 1 гектар (центнеры), а
– количество внесённых минеральных удобрений на 1 гектар (центнеры), а ![]() – соответствующая урожайность картофеля (ц/га – центнеров с га).
– соответствующая урожайность картофеля (ц/га – центнеров с га).
Требуется:
1) Методом наименьших квадратов найти уравнение параболической регрессии ![]() , выполнить чертёж.
, выполнить чертёж.
2) Вычислить индексы детерминации и корреляции и проверить значимость построенной модели на уровне ![]() .
.
3) Вычислить среднюю ошибку аппроксимации.
4) С помощью уравнения регрессии найти оптимальное количество удобрений ![]() , при котором среднеожидаемая урожайность
, при котором среднеожидаемая урожайность ![]() будет максимальной.
будет максимальной.
По каждому пункту сделать выводы.
Все числа уже там, и краткий мануал. 1) Для нахождения коэффициентов регрессии нужно составить и решить следующую систему:

Да, расчётная таблица здесь будет пошире, но с Экселем с этим вообще никаких проблем. Чтобы рассчитать определители используйте функцию =МОПРЕД(выделяем мышкой область три на три).
В пункте 2) следует немного поправить статистический критерий: 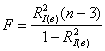 .
.
И по пункту 4): чтобы определить оптимальное количество удобрений, нужно взять производную ![]() и из уравнения
и из уравнения ![]() найти точку максимума
найти точку максимума ![]() . Затем вычислить максимум
. Затем вычислить максимум ![]() .
.
Когда используется параболическая регрессия? Этот вид регрессии уместен там, где по логике задачи должен быть экстремум (минимум или максимум). Так, в Примере 77 логичен тот факт, что при увеличении количества удобрений урожайность сначала растёт, затем достигает максимальных значений и далее падает (т. к. нарастает вред). В Сети я нашёл довольно много примеров из медицины, но смутно понял только один – эквивалентный, когда при увеличении дозировки лекарства активность рецепторов сначала увеличивается, а затем уменьшается. …Эврика! – это ж алкоголь :) Закуска, так сказать, к поданным мной блюдам.
За кадром сегодняшнего урока остался пример с логарифмическое регрессией ![]() , но там всё по шаблону, вот рабочая система:
, но там всё по шаблону, вот рабочая система:
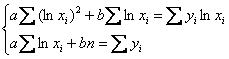 – и понеслось.
– и понеслось.
Далее по курсу коэффициент корреляции Спирмена и коэффициент корреляции Фехнера, ибо не регрессией единой живА корреляционная зависимость.
Решения и ответы:
Пример 75. Решение: 1) Заполним расчётную таблицу:
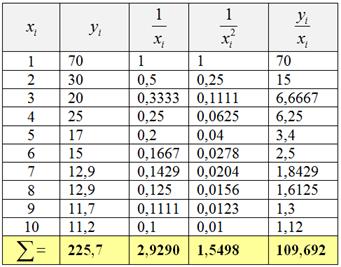
Коэффициенты регрессии ![]() найдём как решение системы:
найдём как решение системы:
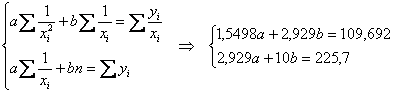
Систему решим по формулам Крамера:
![]() , значит, система имеет единственное решение.
, значит, система имеет единственное решение.
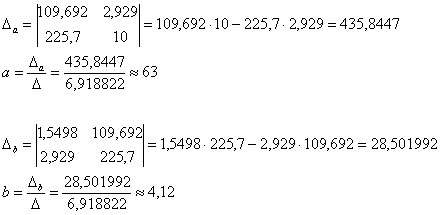
Искомое уравнение: ![]() . Изобразим на чертеже эмпирические точки и график гиперболической регрессии:
. Изобразим на чертеже эмпирические точки и график гиперболической регрессии:
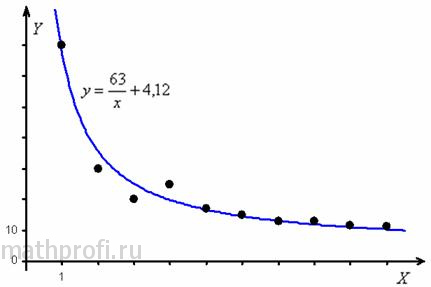
Примечание: для построения гиперболы от руки можно использовать опорные точки ![]() , рассчитанные в таблице ниже.
, рассчитанные в таблице ниже.
По графику хорошо видно, что себестоимость единицы продукции значительно падает при увеличении объёма выпуска до 3-4 тыс. единиц. Дальнейшее увеличение объёма имеет мЕньший эффект и в районе 9-10 тысяч практически перестаёт оказывать влияние на себестоимость.
2) Вычислим среднее значение признака-результата ![]() (руб.) и заполним расчётную таблицу:
(руб.) и заполним расчётную таблицу:
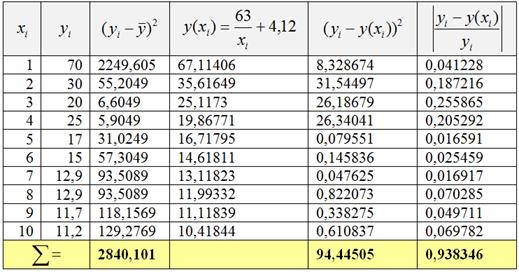
В результате, общая сумма квадратов ![]() , остаточная сумма квадратов
, остаточная сумма квадратов ![]() .
.
Вычислим индекс детерминации:
![]() – таким образом, в рамках построенной модели вариация себестоимости на 96,77% объяснена изменением объёма производства. Остальные 3,33% вариации обусловлены неучтёнными в модели факторами.
– таким образом, в рамках построенной модели вариация себестоимости на 96,77% объяснена изменением объёма производства. Остальные 3,33% вариации обусловлены неучтёнными в модели факторами.
Вычислим индекс корреляции:
![]() – таким образом, себестоимость единицы продукции очень сильно зависит от объёма выпуска.
– таким образом, себестоимость единицы продукции очень сильно зависит от объёма выпуска.
3) На уровне значимости ![]() проверим нулевую гипотезу
проверим нулевую гипотезу ![]() – о том, что генеральный индекс детерминации равен нулю, против конкурирующей гипотезы:
– о том, что генеральный индекс детерминации равен нулю, против конкурирующей гипотезы: ![]() . Используем статистический критерий
. Используем статистический критерий 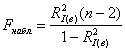 , где
, где ![]() – значение выборочного индекса детерминации.
– значение выборочного индекса детерминации.
Для уровня значимости ![]() и количества степеней свободы
и количества степеней свободы ![]() по соответствующей таблице или с помощью Расчётного макета (пункт 12) определяем критическое значение критерия:
по соответствующей таблице или с помощью Расчётного макета (пункт 12) определяем критическое значение критерия: ![]()
Наблюдаемое значение критерия ![]() попало в критическую область
попало в критическую область ![]() :
:

– поэтому на уровне значимости ![]() гипотезу
гипотезу ![]() отвергаем в пользу гипотезы
отвергаем в пользу гипотезы ![]() .
.
Вывод: выборочный индекс детерминации ![]() статистически значим, следовательно, статистически значимо и выборочное уравнение
статистически значим, следовательно, статистически значимо и выборочное уравнение ![]() гиперболической регрессии.
гиперболической регрессии.
4) Вычислим среднюю ошибку аппроксимации:
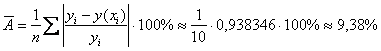 – таким образом, разница между эмпирическими
– таким образом, разница между эмпирическими ![]() и соответствующими регрессионными
и соответствующими регрессионными ![]() значениями составляет в среднем 9,38%, что можно признать неплохим результатом.
значениями составляет в среднем 9,38%, что можно признать неплохим результатом.
Пример 77. Решение:
1) Методом наименьших квадратов найдём уравнение параболической регрессии ![]() . Заполним расчётную таблицу:
. Заполним расчётную таблицу:
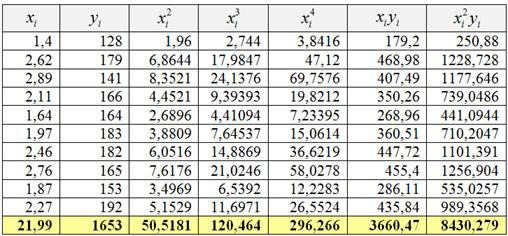
Коэффициенты регрессии найдём как решение системы:
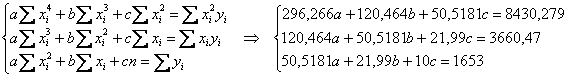
Систему решим по формулам Крамера:
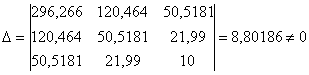 , значит, она имеет единственное решение.
, значит, она имеет единственное решение.
Все определители считаем с помощью функции =МОПРЕД() приложения MS Excel:
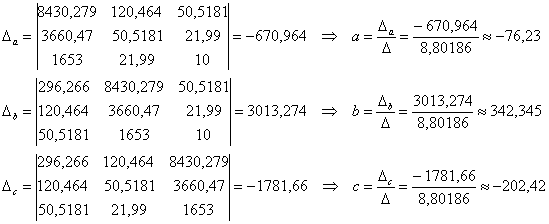
В результате, искомое уравнение: ![]()
Изобразим на чертеже эмпирические точки и линию регрессии:
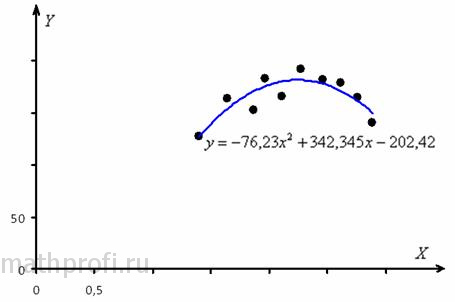
Очевидно, что при увеличении количества вносимых удобрений урожайность сначала растёт (т. к. увеличивается польза), а затем начинает снижаться (т. к. нарастает вред).
2) Вычислим среднее значение урожайности ![]() (ц/г) и заполним расчётную таблицу:
(ц/г) и заполним расчётную таблицу:
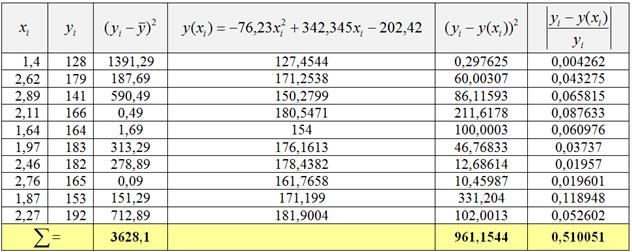
В результате, общая сумма квадратов ![]() , остаточная сумма квадратов
, остаточная сумма квадратов ![]() и индекс детерминации:
и индекс детерминации:
![]() – таким образом, в рамках построенной модели урожайность картофеля на 73,51% зависит от количества внесённых удобрений. Оставшаяся часть вариации (26,49%) урожайности обусловлена другими факторами (составом почвы, погодой и т. д.).
– таким образом, в рамках построенной модели урожайность картофеля на 73,51% зависит от количества внесённых удобрений. Оставшаяся часть вариации (26,49%) урожайности обусловлена другими факторами (составом почвы, погодой и т. д.).
Вычислим индекс корреляции:
![]() – таким образом, зависимость урожайности от количества удобрений – сильная.
– таким образом, зависимость урожайности от количества удобрений – сильная.
На уровне значимости ![]() проверим нулевую гипотезу
проверим нулевую гипотезу ![]() – о том, что генеральный индекс детерминации равен нулю, против конкурирующей гипотезы
– о том, что генеральный индекс детерминации равен нулю, против конкурирующей гипотезы ![]() . Используем статистический критерий
. Используем статистический критерий 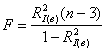 , где
, где ![]() – значение выборочного индекса детерминации.
– значение выборочного индекса детерминации.
Для уровня значимости ![]() и количества степеней свободы
и количества степеней свободы ![]() по соответствующей таблице или с помощью Расчётного макета (пункт 12) определяем критическое значение критерия:
по соответствующей таблице или с помощью Расчётного макета (пункт 12) определяем критическое значение критерия: ![]()
Наблюдаемое значение критерия ![]() , поэтому на уровне значимости
, поэтому на уровне значимости ![]() гипотезу
гипотезу ![]() отвергаем в пользу гипотезы
отвергаем в пользу гипотезы ![]() .
.
Вывод: индекс детерминации ![]() статистически значим, следовательно, статистически значимо и выборочное уравнение
статистически значим, следовательно, статистически значимо и выборочное уравнение ![]() параболической регрессии.
параболической регрессии.
3) Вычислим среднюю ошибку аппроксимации:
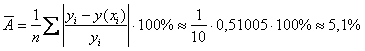 – таким образом, эмпирически
– таким образом, эмпирически ![]() и соответствующие регрессионные значения
и соответствующие регрессионные значения ![]() различаются в среднем на 5,1%, что можно признать очень хорошим результатом.
различаются в среднем на 5,1%, что можно признать очень хорошим результатом.
4) С помощью уравнению регрессии определим оптимальное количество удобрений ![]() и соответствующую среднеожидаемую максимальную урожайность
и соответствующую среднеожидаемую максимальную урожайность ![]() .
.
Найдём производную и приравняем её к нулю:
![]() .
.
Оптимальному количеству удобрений соответствует корень этого уравнения: ![]() центнеров на 1 га.
центнеров на 1 га.
И, согласно полученному уравнению регрессии, этому значению соответствует среднеожидаемая максимальная урожайность:
![]() ц/га
ц/га
Точка с координатами ![]() – есть в точности вершина параболы на чертеже выше. Следует ещё раз заметить, что это среднеожидаемая оценка, полученная по конкретному уравнению регрессии. В другой выборке будет немного другое уравнение и немного другая точка.
– есть в точности вершина параболы на чертеже выше. Следует ещё раз заметить, что это среднеожидаемая оценка, полученная по конкретному уравнению регрессии. В другой выборке будет немного другое уравнение и немного другая точка.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright