


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Поток векторного поля.
Поток через замкнутую поверхность
На втором уроке по основам векторного анализа мы узнаем, что такое поток векторного поля и научимся его находить. Впрочем, некоторые читатели уже знают и умеют ;-)
Начнём с привычного вопроса – а с чем у вас ассоциируется само слово «поток»? …Поток воздуха, поток жидкости…, собственно, о них в частности и пойдёт речь. Откройте окно и вытяните руку в небо. Это будет направление оси ![]() . Другие же оси декартовой системы
. Другие же оси декартовой системы ![]() пусть находятся где-то тут, в комнате.
пусть находятся где-то тут, в комнате.
Теперь открытое окно мысленно «перекроем» непрерывной ![]() -поверхностью. Проще всего выбрать прямоугольный фрагмент плоскости:
-поверхностью. Проще всего выбрать прямоугольный фрагмент плоскости:
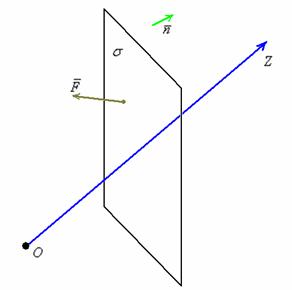
Имеет ли значение сторона поверхности? Конечно. По одну сторону улица, по другую – комната =) Поэтому мы будем рассматривать ориентированную поверхность ![]() с двумя сторонами, которые принято определять с помощью…, ну вы догадываетесь:)
с двумя сторонами, которые принято определять с помощью…, ну вы догадываетесь:)
Сторону, нормальные векторы которой образует с полуосью ![]() острые углы, будем называть положительной стороной и обозначать через
острые углы, будем называть положительной стороной и обозначать через ![]() , и соответственно, противоположную называть отрицательной и обозначать через
, и соответственно, противоположную называть отрицательной и обозначать через ![]() .
.
Примечание: очень хочется сказать «внешняя» и «внутренняя» сторона, но это приведёт к смысловому противоречию – ведь ось ![]() можно развернуть и наоборот. Более того, на её место можно поставить другую координатную ось и определить стороны
можно развернуть и наоборот. Более того, на её место можно поставить другую координатную ось и определить стороны ![]() из аналогичных соображений.
из аналогичных соображений.
Для определённости выберем уличную (положительную сторону), и поскольку наша поверхность плоская, то у ВСЕХ её точек будет один и тот же вектор нормали ![]() . Этот вектор свободен, и его можно начертить где угодно.
. Этот вектор свободен, и его можно начертить где угодно.
Что характерно? В окно дует ветер. Или из окна (мало ли, сквозняк). Рассмотрим поле скоростей воздуха и каждой точке поверхности ![]() поставим в соответствие исходящий из неё несвободный вектор
поставим в соответствие исходящий из неё несвободный вектор ![]() , который указывает направление и скорость движения воздуха в данной точке. Чем сильнее ветер, тем длиннее вектор. Один из них я изобразил на чертеже.
, который указывает направление и скорость движения воздуха в данной точке. Чем сильнее ветер, тем длиннее вектор. Один из них я изобразил на чертеже.
Всё очень просто: поток (обозначается буквой ![]() ) – это количество воздуха, прошедшее через ориентированную поверхность
) – это количество воздуха, прошедшее через ориентированную поверхность ![]() в единицу времени (предполагается, что поле скоростей измениться не успело). Причём:
в единицу времени (предполагается, что поле скоростей измениться не успело). Причём:
– если ![]() , то воздух движется (полностью или преимущественно) по направлению векторов нормали выбранной «уличной» стороны
, то воздух движется (полностью или преимущественно) по направлению векторов нормали выбранной «уличной» стороны ![]() («уходит» из комнаты);
(«уходит» из комнаты);
– если ![]() , то воздух движется (полностью или преимущественно) против вектора
, то воздух движется (полностью или преимущественно) против вектора ![]() (поступает в комнату).
(поступает в комнату).
Чем больше поток по модулю, тем больше воздуха прошло через поверхность (в определённую единицу времени), и тем, понятно, сильнее дует ветер.
– и, наконец, значению ![]() соответствуют практически невероятные ситуации:
соответствуют практически невероятные ситуации:
1) абсолютный штиль (ветер не дует вообще);
2) ветер дует строго в самой плоскости «сигма» (все векторы «эф» лежат в ней);
3) равновесие – сколько воздуха «пришло» через поверхность, столько и «ушло».
Что изменится, если рассмотреть «комнатную» сторону ![]() поверхности? Поскольку её нормальный вектор направлен в противоположную сторону, то изменится знак потока:
поверхности? Поскольку её нормальный вектор направлен в противоположную сторону, то изменится знак потока:
– он станет отрицательным, когда воздух «уходит» на улицу, и положительным, когда ветер дует в окно. Образно говоря, здесь мы будем смотреть на ту же самую ситуацию, только с другой стороны.
Вообще, чтобы учащиеся лучше прочувствовали эти тонны потока, во многих источниках информации приводится аналогичный пример с жидкостью. Но уж «Титаник» мы устраивать не будем, это грустный фильм – лучше откройте водопроводный кран, задайте координатную ось и проанализируйте поток воды через сечение водопроводной трубы. Хорошего вам напора!
Но кроме шуток, классический пример с жидкостью не случаен – по той причине, что понятие потока пришло именно из гидродинамики, после чего распространилось на произвольное векторное поле, где зачастую «дуть» или «течь» в прямом смысле нечему.
Теперь абстрагируемся от конкретных примеров и перейдём к общим формулировкам:
Поток векторного поля ![]() через ориентированную поверхность
через ориентированную поверхность ![]() в единицу времени численно равен поверхностному интегралу 2-го рода по этой поверхности:
в единицу времени численно равен поверхностному интегралу 2-го рода по этой поверхности:
![]()
Если объяснять просто, то из каждой точки поверхности ![]() торчит вектор
торчит вектор ![]() поля, и, согласно общему принципу интегрирования, данный интеграл объединяет бесконечно малые проекции всех этих векторов на координатные плоскости, что и является мерилом суммарного потока.
поля, и, согласно общему принципу интегрирования, данный интеграл объединяет бесконечно малые проекции всех этих векторов на координатные плоскости, что и является мерилом суммарного потока.
И во 2-й части урока Поверхностные интегралы (Примеры № 5-8), мы только и занимались тем, что находили поток векторного поля. А если не занимались, то таки придётся, ибо без техники решения никуда. Дальнейшее изложение материала предполагает, что вы умеете решать поверхностные интегралы.
Так, например, вспомним Пример 5:
«Вычислить интеграл ![]() , где
, где ![]() – верхняя сторона плоскости
– верхняя сторона плоскости ![]() , расположенная в 1 октанте»
, расположенная в 1 октанте»
Скопирую оттуда чертёж:
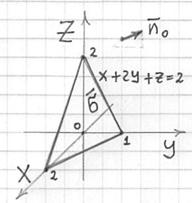
Условие этой задачи можно сформулировать эквивалентно:
«Найти поток векторного поля ![]() через часть плоскости
через часть плоскости ![]() , ограниченную координатными плоскостями, в направлении вектора нормали, образующего с положительной полуосью
, ограниченную координатными плоскостями, в направлении вектора нормали, образующего с положительной полуосью![]() острый угол»:
острый угол»:
В том примере мы получили ответ ![]() – это и есть поток векторного поля через верхнюю сторону треугольника.
– это и есть поток векторного поля через верхнюю сторону треугольника.
Что означает этот результат в гидродинамическом смысле? Он означает, что за единицу времени в направлении вектора ![]() протекло 5 единиц жидкости. Если бы результат получился отрицательным, то это бы означало, что «утечка» произошла в противоположном направлении.
протекло 5 единиц жидкости. Если бы результат получился отрицательным, то это бы означало, что «утечка» произошла в противоположном направлении.
Если вычислить поверхностный интеграл по нижней стороне треугольника, то поток сменит знак:
![]()
Здесь мы «посмотрели на ситуацию» с другой стороны – по направлению противоположно направленного нормального вектора ![]() . Само же векторное поле (направление и скорость течения воды) нисколько не изменилось.
. Само же векторное поле (направление и скорость течения воды) нисколько не изменилось.
Я снова воздержусь от секунд, килограммов и прочих физических величин, чтобы сосредоточиться на математической стороне вопроса. Скажу только, что поверхностные интегралы нашли широкое применение в различных разделах физики, и на самом деле – это отдельная большая тема для разговора.
Как найти поток векторного поля?
Начинающим, да и всем остальным рекомендую по возможности сводить решение к вычислению поверхностного интеграла 1-го рода:
![]()
Просто чтобы не запутаться.
В основе этого перехода лежит известная формула скалярного произведения ![]() , и тут будет полезно проанализировать её содержательный смысл. Пусть
, и тут будет полезно проанализировать её содержательный смысл. Пусть ![]() – это единичный вектор нормали «комнатой» стороны нашего «сигма-окна» и пусть в рассматриваемых ниже ситуациях дует ветер некоторой постоянной скорости.
– это единичный вектор нормали «комнатой» стороны нашего «сигма-окна» и пусть в рассматриваемых ниже ситуациях дует ветер некоторой постоянной скорости.
Теперь ответим на вопрос: когда поток будут максимальным? Математически максимум достигается при ![]() , то есть когда углы между «полевыми» и нормальным вектором равны нулю. Что это значит? Это значит, что ветер дует «прямо в окно» – строго по направлению нормалей. Логично, что именно в этом случае в комнату и попадёт максимальное количество воздуха.
, то есть когда углы между «полевыми» и нормальным вектором равны нулю. Что это значит? Это значит, что ветер дует «прямо в окно» – строго по направлению нормалей. Логично, что именно в этом случае в комнату и попадёт максимальное количество воздуха.
Если «угол задува» увеличивать от 0 до 90 градусов, то косинус (а значит, и поток) будет уменьшаться до нуля. Тоже логично. В частности, если ветер (такой же силы!) дует в окно под углом в 60 градусов, то поток воздуха по абсолютной величине будет уже в два раза меньше ![]() .Случаю
.Случаю ![]() соответствует «невероятная ситуация», когда воздух перемещается в «плоскости окна». И, наконец, отрицательным значениям косинуса (углы от 90 до 180 градусов) соответствуют случаи, когда ветер дует против вектора нормали (т.е. из окна).
соответствует «невероятная ситуация», когда воздух перемещается в «плоскости окна». И, наконец, отрицательным значениям косинуса (углы от 90 до 180 градусов) соответствуют случаи, когда ветер дует против вектора нормали (т.е. из окна).
Ещё раз призываю научиться решать поверхностные интегралы тех, кто не успел этого сделать, поскольку сейчас мы фактически продолжаем тему:
Поток векторного поля через замкнутую поверхность
Наверное, все интуитивно понимают, что это за поверхность. К простейшим замкнутым поверхностям можно отнести сферу и треугольную пирамиду.
Вычисление потока через замкнутую поверхность имеет свои особенности, с которыми мы познакомимся в ходе решения следующего каноничного примера:
Пример 1
Найти поток векторного поля ![]() через замкнутую поверхность, ограниченную плоскостью
через замкнутую поверхность, ограниченную плоскостью ![]() и координатными плоскостями, в направлении внешней нормали
и координатными плоскостями, в направлении внешней нормали
Решение, как повелось, начинаем с чертежа. Перепишем уравнение плоскости в отрезках ![]() и изобразим предложенную поверхность, которая представляет собой треугольную пирамиду:
и изобразим предложенную поверхность, которая представляет собой треугольную пирамиду:
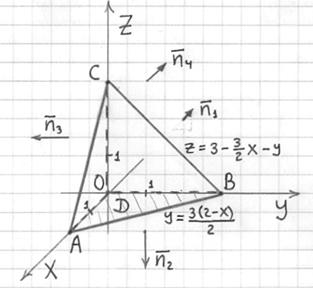
По условию, поверхность ориентирована в направлении внешней нормали, и поэтому к обозначению пирамиды я добавлю условную стрелочку: ![]() .
.
Поток векторного поля вычислим с помощью того же поверхностного интеграла 2-го рода, и так как поверхность замкнута, то к его обозначению обычно добавляют символический кружочек:
![]()
Если совсем тяжко, используйте привычную «сигму»:
![]() , подразумевая под чёрточкой внешнее направление. Заметьте также, что здесь крайне нежелательно ставить «плюсик»:
, подразумевая под чёрточкой внешнее направление. Заметьте также, что здесь крайне нежелательно ставить «плюсик»: ![]() – по той причине, что три грани пирамиды «смотрят» против координатных осей!
– по той причине, что три грани пирамиды «смотрят» против координатных осей!
Несмотря на «страшный вид», смысл задачи опять же прост: представьте, что пирамида ограничивает фрагмент нЕкоего водного русла. Требуется выяснить, сколько жидкости туда поступило/вытекло в единицу времени.
И, очевидно, что здесь придётся воспользоваться свойством аддитивности поверхностного интеграла, а конкретнее, представить его в виде суммы четырёх поверхностных интегралов по ориентированным граням пирамиды:
![]() , где:
, где:
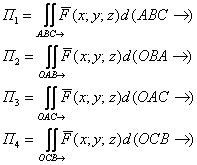
Здесь можно тоже использовать короткие обозначения ![]() , но чтобы всё было понятнее, я предпочёл пусть громоздкие, но зато «говорящие» названия поверхностей.
, но чтобы всё было понятнее, я предпочёл пусть громоздкие, но зато «говорящие» названия поверхностей.
! Примечание: вершины треугольников (и др. фигур) желательно перечислять по правилу штопора: представьте, что вы вкручиваете его в бутылку по направлению вектора нормали. Тогда вершины следует перечислить по направлению вращательного движения ручки штопора. Это правило дополнительно и однозначно указывает на ориентацию поверхности.
…что-то не вижу энтузиазма в ваших глазах:)) …и напрасно – с каждым экраном будет всё интереснее и интереснее ;)
1) Вычислим поток векторного поля через ориентированный треугольник ![]() в направлении нормального вектора
в направлении нормального вектора ![]() . По сути дела, это Пример 5 урока Поверхностные интегралы.
. По сути дела, это Пример 5 урока Поверхностные интегралы.
Поскольку внешняя нормаль образует с полуосью ![]() острый угол, то для нахождения единичного нормального вектора используем формулу:
острый угол, то для нахождения единичного нормального вектора используем формулу:
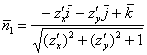
Запишем функцию плоскости ![]() :
:
![]()
и найдём частные производные 1-го порядка:
![]()
Таким образом:
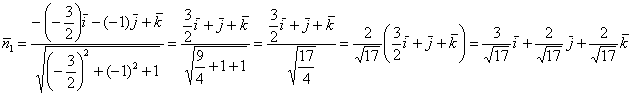
Убедимся, что его длина действительно равна единице:
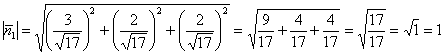 , ч.т.п. На чертеже он выглядит коротеньким, но что поделать – такой уж наклон плоскости.
, ч.т.п. На чертеже он выглядит коротеньким, но что поделать – такой уж наклон плоскости.
Вычислим скалярное произведение:
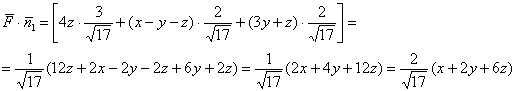
и сведём решение к вычислению поверхностного интеграла 1-го рода:
![]()
Теперь используем формулу ![]() , где
, где ![]() – проекция поверхности «сигма» на плоскость
– проекция поверхности «сигма» на плоскость ![]() . Напоминаю, что интеграл 1-го рода можно вычислить ещё двумя способами, но во избежание путаницы (опять же) лучше пойти привычным путём:
. Напоминаю, что интеграл 1-го рода можно вычислить ещё двумя способами, но во избежание путаницы (опять же) лучше пойти привычным путём:
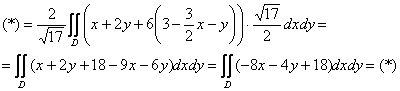
Осталось разрулить двойной интеграл. Найдём прямую, по которой пересекаются плоскости ![]() и
и ![]() :
:
![]()
и изобразим проекцию ![]() на двумерном чертеже (не ленимся!!!):
на двумерном чертеже (не ленимся!!!):
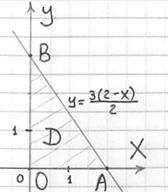
Очевидно, что с порядком обхода я уже определился чуть ранее:
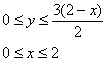
Продолжаем:
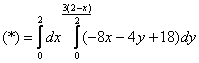
Повторные интегралы удобнее вычислить по порядку. Сначала внутренний:
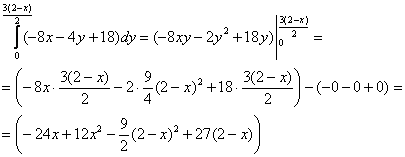
затем внешний:

Готово. Обратите внимание на рациональную технику вычисления и оформления.
Для лучшего понимания задачи продолжим вкладывать в решение гидродинамический смысл. Что означает полученный результат ![]() ? Он означает, что за единицу времени через треугольник
? Он означает, что за единицу времени через треугольник ![]() в направлении вектора
в направлении вектора ![]() прошло 26 единиц жидкости. Кстати, это не значит, что она движется ИСКЛЮЧИТЕЛЬНО в данном направлении. Вполне возможно, что здесь «водоворот»: попробуйте поподставлять в функцию
прошло 26 единиц жидкости. Кстати, это не значит, что она движется ИСКЛЮЧИТЕЛЬНО в данном направлении. Вполне возможно, что здесь «водоворот»: попробуйте поподставлять в функцию ![]() различные точки треугольника
различные точки треугольника ![]() , и если окажется, что векторы поля торчат из него в разные стороны, то дело обстоит именно так.
, и если окажется, что векторы поля торчат из него в разные стороны, то дело обстоит именно так.
Оставшиеся три интеграла, благо, проще:
2) Найдём поток векторного поля через ориентированный треугольник ![]() . Единичный вектор нормали тут очевиден:
. Единичный вектор нормали тут очевиден: ![]() или
или ![]() . Вычислим скалярное произведение:
. Вычислим скалярное произведение:
![]()
и перейдём к поверхностному интегралу 1-го рода
![]()
Так как поверхность лежит непосредственно в плоскости ![]() , то формула
, то формула
![]() сильно упрощается – ведь «зет» и её производные равны нулю. Двойной интеграл возьмём по тем же пределам интегрирования:
сильно упрощается – ведь «зет» и её производные равны нулю. Двойной интеграл возьмём по тем же пределам интегрирования:

Отрицательное значение ![]() означает, что за единицу времени через треугольник
означает, что за единицу времени через треугольник ![]() по итогу прошло 9 единиц жидкости против вектора
по итогу прошло 9 единиц жидкости против вектора ![]() (то есть, поступило внутрь пирамиды). Любопытные читатели могут снова поподставлять точки треугольника в функцию
(то есть, поступило внутрь пирамиды). Любопытные читатели могут снова поподставлять точки треугольника в функцию ![]() и проанализировать характер течения.
и проанализировать характер течения.
3) Вычислим поток векторного поля через ориентированный треугольник ![]() . Внешняя нормаль здесь тоже как на ладони:
. Внешняя нормаль здесь тоже как на ладони: ![]() или
или ![]() . Скалярное произведение:
. Скалярное произведение:
![]()
и стандартный переход:
![]()
Поскольку треугольник ![]() лежит в плоскости
лежит в плоскости ![]() , то используем формулу
, то используем формулу ![]() , в которой поверхность
, в которой поверхность ![]() совпадает со своей проекцией
совпадает со своей проекцией ![]() на плоскость
на плоскость ![]() , а функция
, а функция ![]() вместе со своими производными равна нулю:
вместе со своими производными равна нулю:
![]()
Найдём прямую, по которой пересекаются плоскости:
![]()
и выполним двумерный чертёж:
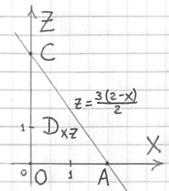
По размерам треугольник равен предыдущему, но это только размеры. Выберем следующий порядок обхода области:
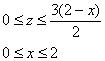
и перейдём к повторным интегралам:

Внутренний:
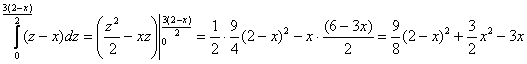
и внешний:
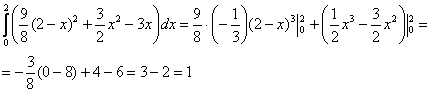
Результат ![]() означает, что за единицу времени через плоскость
означает, что за единицу времени через плоскость ![]() протекла 1 единица жидкости в направлении вектора
протекла 1 единица жидкости в направлении вектора ![]() (убыла из пирамиды). Может быть, здесь очень слабое течение, но не исключено, что и бурный водоворот. Исследуете вопрос методом научного тыка!
(убыла из пирамиды). Может быть, здесь очень слабое течение, но не исключено, что и бурный водоворот. Исследуете вопрос методом научного тыка!
4) И, наконец, поток векторного поля через грань ![]() по внешнему направлению
по внешнему направлению ![]() Скалярное произведение:
Скалярное произведение:
![]()
и ещё раз переход:
![]()
Поскольку треугольник находится в плоскости ![]() , то пускаем в ход формулу
, то пускаем в ход формулу ![]() , где функция
, где функция ![]() и её производные равны нулю:
и её производные равны нулю:
![]()
Найдём линию пересечения плоскостей и выполним двумерный чертёж:
![]()
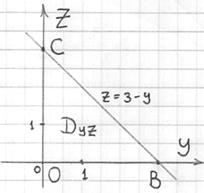
Выберем следующий порядок обхода области:
![]()
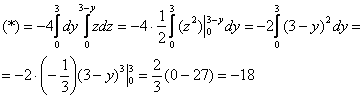
Отрицательное значение ![]() означает, что за единицу времени через треугольник
означает, что за единицу времени через треугольник ![]() по итогу протекло 18 единиц жидкости против направления вектора
по итогу протекло 18 единиц жидкости против направления вектора ![]() (т.е. внутрь пирамиды).
(т.е. внутрь пирамиды).
Ну что же, вот и настал этот знаменательный момент. Вычислим поток векторного поля через всю пирамиду по направлению внешних нормалей:
![]()
Ответ: ![]()
Что это значит? Это значит, что в единицу времени – сколько поступило жидкости внутрь пирамиды – столько и вытекло.
Да, решение длинное, да решение непростое, но задачи на вычисление потока векторного поля встречаются даже у студентов-заочников, причём, довольно часто. И поэтому обязательно потренируйтесь на небольшой призмочке:
Пример 2
Вычислить поток векторного поля ![]() через замкнутую поверхность
через замкнутую поверхность ![]() в направлении внешней нормали
в направлении внешней нормали
![]()
Будьте ОЧЕНЬ внимательны!
В ходе решения заметьте, что плоскости ![]() параллельны оси
параллельны оси ![]() , а точнее проходят через неё, и поэтому проецирование на плоскость
, а точнее проходят через неё, и поэтому проецирование на плоскость ![]() не годится; плоскость же
не годится; плоскость же ![]() параллельна плоскости
параллельна плоскости ![]() и здесь вообще один вариант.
и здесь вообще один вариант.
Кроме того, нормальные векторы плоскостей ![]() ортогональны к оси
ортогональны к оси ![]() , и до сих пор нам не встречалась эта ситуация. Как их найти? Здесь можно обойтись стандартными формулами (см. по ссылке выше), после чего проверить, куда они «смотрят» (графически или вычислив скалярное произведение с вектором
, и до сих пор нам не встречалась эта ситуация. Как их найти? Здесь можно обойтись стандартными формулами (см. по ссылке выше), после чего проверить, куда они «смотрят» (графически или вычислив скалярное произведение с вектором ![]() либо
либо![]() ).
).
Но что делать, если дана произвольная поверхность? И вообще – нужно ли исследовать всю поверхность? Перейдём ко 2-й части статьи, где нас ждёт множество удивительных открытий:
Дивергенция векторного поля >>>
! Перейдите к ней ПРЯМО СЕЙЧАС и прочитайте по «горячим мыслям» хотя бы начало!
Решение Примера 2:
Изобразим на чертеже искомую поверхность, это призма ![]() :
:
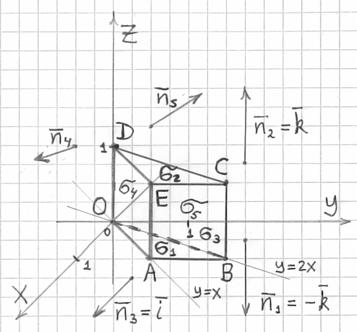
Поток ![]() векторного поля
векторного поля ![]() через внешне-ориентированную поверхность
через внешне-ориентированную поверхность ![]() вычислим с помощью поверхностного интеграла 2-го рода путём перехода к интегралу 1-го рода:
вычислим с помощью поверхностного интеграла 2-го рода путём перехода к интегралу 1-го рода:
![]() , где
, где ![]() – единичный вектор внешней нормали.
– единичный вектор внешней нормали.
Поток представим в виде суммы 5 потоков через грани призмы:
![]()
1) Вычислим поток ![]() через ориентированную грань
через ориентированную грань ![]() в направлении единичного нормального вектора
в направлении единичного нормального вектора ![]() . Найдём скалярное произведение:
. Найдём скалярное произведение:
![]()
Таким образом:
![]() , поскольку грань
, поскольку грань ![]() лежит в плоскости
лежит в плоскости ![]() .
.
2) Вычислим поток ![]() через грань
через грань ![]() в направлении единичного нормального вектора
в направлении единичного нормального вектора ![]() . Найдём скалярное произведение:
. Найдём скалярное произведение:
![]()
Таким образом:
![]()
используем формулу:
![]()
Грань ![]() лежит в плоскости
лежит в плоскости ![]() , следовательно,
, следовательно, ![]() и:
и:
![]()
Изобразим проекцию грани ![]() на плоскость
на плоскость ![]() :
:
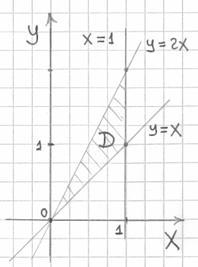
и выберем следующий порядок обхода области:
![]()
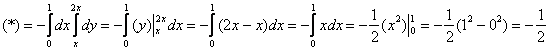
3) Вычислим поток ![]() через грань
через грань ![]() в направлении единичного нормального вектора
в направлении единичного нормального вектора ![]() . Найдём скалярное произведение:
. Найдём скалярное произведение:
![]()
Таким образом:
![]()
Квадрат ![]() лежит в плоскости
лежит в плоскости ![]() и удачно проецируется лишь на плоскость
и удачно проецируется лишь на плоскость ![]() . Используем формулу
. Используем формулу ![]() , в данном случае
, в данном случае ![]() и:
и:
![]()
Изобразим проекцию грани ![]() на плоскость
на плоскость ![]() :
:
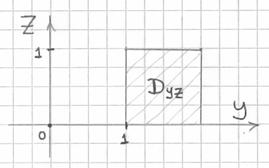
и выберем следующий порядок обхода области:
![]()
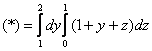
а) 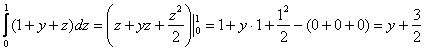
б) 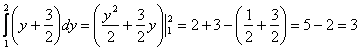
4) Вычислим поток ![]() через грань
через грань ![]() . Найдём вектор
. Найдём вектор ![]() . Данная грань лежит в плоскости
. Данная грань лежит в плоскости ![]() с нормальным вектором
с нормальным вектором ![]() . Тогда соответствующий вектор единичной длины:
. Тогда соответствующий вектор единичной длины:
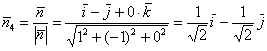
Контроль: 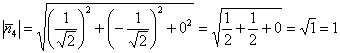
Примечание: ![]() – это именно тот вектор, который «смотрит» во внешнем направлении грани
– это именно тот вектор, который «смотрит» во внешнем направлении грани ![]() , аналитически это можно выяснить с помощью скалярного произведения:
, аналитически это можно выяснить с помощью скалярного произведения:
![]() , значит, между ним и координатным вектором
, значит, между ним и координатным вектором ![]() острый угол.
острый угол.
Таким образом:
![]()
![]()
Грань ![]() несколько удобнее спроецировать на плоскость
несколько удобнее спроецировать на плоскость ![]() . Используем формулу
. Используем формулу ![]() . Из уравнения плоскости
. Из уравнения плоскости ![]() выразим
выразим ![]() и найдём
и найдём ![]()
![]()
Изобразим проекцию грани ![]() на плоскость
на плоскость ![]() :
:
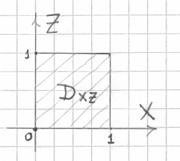
и выберем следующий порядок обхода области:
![]()

5) Вычислим поток ![]() через грань
через грань ![]() в направлении
в направлении ![]() внешней нормали. Данная грань лежит в плоскости
внешней нормали. Данная грань лежит в плоскости ![]() с нормальным вектором
с нормальным вектором ![]() . Но нас устраивает вектор, который образует с вектором
. Но нас устраивает вектор, который образует с вектором ![]() тупой угол, и это противоположно направленный вектор
тупой угол, и это противоположно направленный вектор ![]() (и в самом деле:
(и в самом деле: ![]() , значит, между этими векторами тупой угол). Найдём соответствующий единичный вектор:
, значит, между этими векторами тупой угол). Найдём соответствующий единичный вектор:
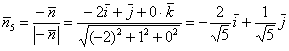
Контроль: 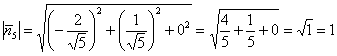
Таким образом:
![]()
![]()
Грань ![]() спроецируем на ту же плоскость
спроецируем на ту же плоскость ![]() – в тот же квадрат (см. чертёж предыдущего пункта). Используем формулу
– в тот же квадрат (см. чертёж предыдущего пункта). Используем формулу ![]() . Из уравнения плоскости
. Из уравнения плоскости ![]() выразим
выразим ![]() и найдём
и найдём ![]()
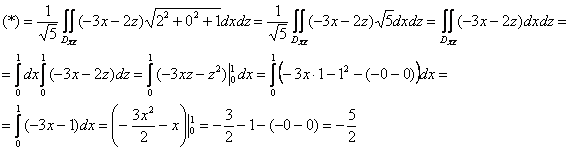
В результате поток векторного поля через всю призму:
![]()
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright