Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

19. Линейный коэффициент корреляции

Эта тема планировалась более 10 лет назад и вот, наконец, я здесь…. И вы здесь! И это замечательно! Даже не то слово. Это корреляционно.

О корреляции речь зашла в статьях об аналитической и комбинационной группировке, в результате чего перед нами нарисовались некоторые эмпирические показателями корреляции (прочитайте хотя бы «по диагонали»!). И сейчас на очереди линейный коэффициент корреляции, популярный настолько, что по умолчанию под коэффициентом корреляции понимают именно его. …Да, всё верно – существует довольно много разных коэффициентов корреляции. Однако всему своё время.

Материал данной темы состоит из двух уровней:

– начального, для всех – вплоть до студентов психологических и социологических факультетов, блондинок, брюнеток, школьников, бабушек, дедушек, etc и

– продвинутого, где я разберу более редкие задачи, а некоторые даже не буду разбирать :)

В результате вы научитесь БЫСТРО решать типовые задачи (видео прилагается) и для самых ленивых есть калькуляторы. И пока не запамятовал, хочу порекомендовать корреляционно-регрессионный анализ для ваших научных работ и практических исследований – наряду со статистическими гипотезами, это самая настоящая находка в плане новизны и творческих изысканий.

! Предупреждение: в рамках сайта я рассматриваю лишь азы и учебные задачи, для выбора методов в серьёзных исследованиях лучше задействовать другие источники.

Оглавление:

– диаграмма рассеяния;
– уравнение линейной регрессии – его разберём с опережением;
– линейный коэффициент корреляции;
– коэффициент детерминации

и по просьбам учащихся:

– коэффициент средней эластичности;
– бета-коэффициент,

то было для «чайников», для начала достаточно…

…И в этот момент я благоговейно улыбаюсь – как здорово, что все мы здесь сегодня собрались:

Пример 67

Имеются выборочные данные по  студентам:  – количество прогулов за некоторый период времени и  – суммарная успеваемость за этот период:

И сразу обращаю внимание, что в условии приведены несгруппированные данные. Помимо этого варианта, есть задачи, где изначально дана комбинационная таблица, и их мы тоже разберём. Сначала одно, затем другое.

Требуется:

1) высказать предположение о наличии и направлении корреляционной зависимости признака-результата  от признака-фактора  и построить диаграмму рассеяния;

2) анализируя диаграмму рассеяния, сделать вывод о форме зависимости;

3) найти уравнение линейной регрессии  на , выполнить чертёж;

4) вычислить линейный коэффициент корреляции, сделать вывод;

5) вычислить коэффициент детерминации, сделать вывод;

6) вычислить коэффициент эластичности и

7) вычислить бета-коэффициент, с выводами, понятное дело,

и для продвинутых читателей – проверка значимости линейной модели и иже с ней потрохами, а также вся анатомия.

Решение:

1) Прежде всего, повторим, что такое корреляционная зависимость. Очевидно, что чем больше студент прогуливает, тем более вероятно, что у него плохая успеваемость. Но всегда ли это так? Нет, не всегда. Успеваемость зависит от многих факторов. Один студент может посещать все пары, но все равно учиться посредственно, а другой – учиться неплохо даже при достаточно большом количестве прогулов. Однако общая тенденция состоит в том, что с увеличением количества прогулов средняя успеваемость студентов будет падать. Такая нежёсткая зависимость и называется корреляционной.

По своему направлению зависимость бывает прямой («чем больше, тем больше») и обратной («чем больше, тем меньше»). В данной задаче мы высказали предположение о наличии обратной корреляционной зависимости  – успеваемости студентов от  – количества их прогулов. И что немаловажно, обосновали причинно-следственную связь (читать всем!!!) между признаками.

Проверить выдвинутое предположение проще всего графически, и в этом нам поможет:

диаграмма рассеяния

– это множество точек  в декартовой системе координат, абсциссы  которых соответствуют значениям признака-фактора , а ординаты  – соответствующим значениям признака-результата .  Минимальное количество точек должно равняться пяти-шести, в противном случае рассматриваемая задача превращается в профанацию. И мы «вписываемся в рамки» – объём выборки равен восьми студентам:

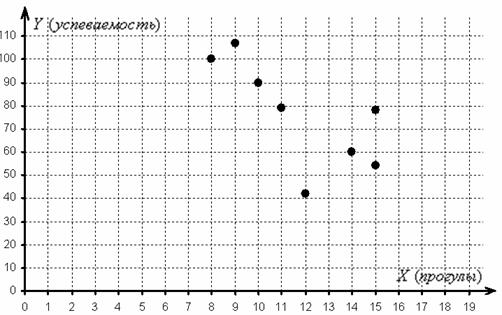
Обратите, кстати, внимание как раз на тот момент, что при одном и том же количестве прогулов (15) двое студентов имеют существенно разные результаты.

2) По диаграмме рассеяния хорошо видно, что с увеличением числа прогулов успеваемость преимущественно падает, что подтверждает наличие обратной корреляционной зависимости успеваемости от количества прогулов. Более того, почти все точки «выстроились» примерно по прямой, что даёт основание предположить, что данная зависимость близкА к линейной.

И здесь я анонсирую дальнейшие действия: сейчас нам предстоит найти уравнение прямой, ТАКОЙ, которая проходит максимально близко к эмпирическим точкам, а также оценить тесноту линейной корреляционной зависимости – насколько близко расположены эти точки к построенной прямой.

Технически существует два пути решения:

– сначала найти уравнение прямой и затем оценить тесноту зависимости;
– сначала найти тесноту и затем составить уравнение.

В практически задачах чаще встречается второй вариант, но я начну с первого, он более последователен. Построим:

3) уравнение линейной регрессии 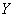 на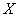

Это и есть та самая оптимальная прямая , которая проходит максимально близко к эмпирическим точкам. Обычно её находят методом наименьших квадратов, и мы пойдём знакомым путём. Заполним расчётную таблицу:

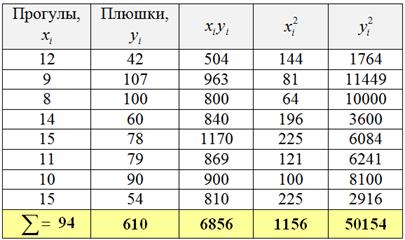
Обратите внимание, что в отличие от задач урока МНК у нас появился дополнительный столбец , он потребуется в дальнейшем, для расчёта коэффициента корреляции.

Коэффициенты функции  найдём из решения системы:

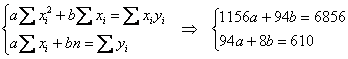
Сократим оба уравнения на 2, всё попроще будет:

Систему решим по формулам Крамера:
, значит, система имеет единственное решение.

И проверка forever, подставим полученные значения  в левую часть каждого уравнения исходной системы:

в результате получены соответствующие правые части, значит, система решена верно.

Таким образом, искомое уравнение регрессии:
 

Данное уравнение показывает, что с увеличением количества прогулов («икс») на 1 единицу суммарная успеваемость падает в среднем на 6,0485 – примерно на 6 баллов. Об этом нам рассказал коэффициент «а». И обратите особое внимание, что эта функция возвращает нам средние (среднеожидаемые) значения «игрек» для различных значений «икс».

Почему это регрессия именно « на » и о происхождении самого термина «регрессия» я рассказал чуть ранее, в параграфе эмпирические линии регрессии. Если кратко, то полученные с помощью уравнения средние значения успеваемости («игреки») регрессивно возвращают нас к первопричине – количеству прогулов. Вообще, регрессия – не слишком позитивное слово, но какое уж есть.

Найдём пару удобных точек для построения прямой:

отметим их на чертеже (малиновый цвет) и проведём линию регрессии:

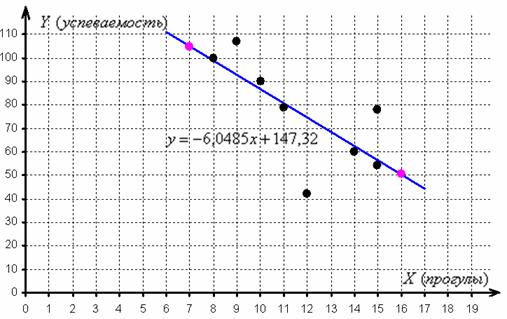
Говорят, что уравнение регрессии аппроксимирует (приближает) эмпирические данные (точки), и с помощью него можно интерполировать (оценить) неизвестные промежуточные значения, так при количестве прогулов  среднеожидаемая успеваемость составит  балла.

И, конечно, осуществимо прогнозирование, так при  среднеожидаемая успеваемость составит  баллов. Единственное, нежелательно брать «иксы», которые расположены слишком далеко от эмпирических точек, поскольку прогноз, скорее всего, не будет соответствовать действительности. Например, при  значение  может вообще оказаться невозможным, ибо у успеваемости есть свой фиксированный «потолок». И, разумеется, «икс» или «игрек» в нашей задаче не могут быть отрицательными.

Второй вопрос касается тесноты зависимости. Очевидно, что чем ближе эмпирические точки к прямой, тем теснее линейная корреляционная зависимость – тем уравнение регрессии достовернее отражает ситуацию, и тем качественнее полученная модель. И наоборот, если многие точки разбросаны вдали от прямой, то признак  зависит от  вовсе не линейно (если вообще зависит) и линейная функция плохо отражает реальную картину.

Прояснить данный вопрос нам поможет:

4) линейный коэффициент корреляции

Этот коэффициент как раз и оценивает тесноту линейной корреляционной зависимости и более того, указывает её направление (прямая или обратная). Его полное название: выборочный линейный коэффициент пАрной корреляции Пирсона :)

– «выборочный» – потому что мы рассматриваем выборочную совокупность;
– «линейный» – потому что он оценивает тесноту линейной корреляционной зависимости;
– «пАрной» – потому что у нас два признака (бывает хуже);
– и «Пирсона» – в честь английского статистика Карла Пирсона, это он автор понятия «корреляция».

И в зависимости от фантазии автора задачи вам может встретиться любая комбинация этих слов. Теперь нас не застанешь врасплох, Карл.

Линейный коэффициент корреляции вычислим по формуле:
, где:  – среднее значение произведения признаков,  – средние значения признаков и  – стандартные отклонения признаков. Числитель формулы имеет особый смысл, о котором я расскажу, когда мы будем разбирать второй способ решения.

Осталось разгрести всё это добро :) Впрочем, все нужные суммы уже рассчитаны в таблице выше. Вычислим средние значения:

Стандартные отклонения найдём как корни из соответствующих дисперсий, вычисленных по формуле:

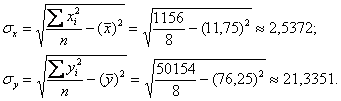
Таким образом, коэффициент корреляции:

И расшифровка: коэффициент корреляции может изменяться в пределах  и чем он ближе по модулю к единице, тем теснее линейная корреляционная зависимость – тем ближе расположены точки к прямой, тем качественнее и достовернее линейная модель. Если  либо , то речь идёт о строгой линейной зависимости, при которой все эмпирические точки окажутся на построенной прямой. Наоборот, чем ближе  к нулю, тем точки рассеяны дальше, тем линейная зависимость выражена меньше. Однако в последнем случае зависимость всё равно может быть! – например, нелинейной или какой-нибудь более загадочной. Но до этого мы ещё дойдём. А у кого не хватит сил, донесём :)

Для оценки тесноты связи будем использовать уже знакомую шкалу Чеддока:

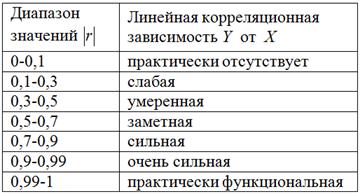
При этом если , то корреляционная связь обратная, а если , то прямая.

В нашем случае , таким образом, существует сильная обратная линейная корреляционная зависимость  – суммарной успеваемости от  – количества прогулов.

Линейный коэффициент корреляции – это частный аналог эмпирического корреляционного отношения. Но в отличие от отношения, он показывает не только тесноту, но ещё и направление зависимости, ну и, конечно, здесь определена её форма (линейная).

5) Коэффициент детерминации

– это частный аналог эмпирического коэффициента детерминации – есть квадрат коэффициента корреляции:

 – коэффициент детерминации показывает долю вариации признака-результата , которая обусловлена воздействием признака-фактора . С математическим обоснованием этого утверждения желающие могут ознакомиться в статье Однофакторная регрессия.

В нашей задаче:
 – таким образом, в рамках построенной модели успеваемость на 51,74% зависит от количества прогулов. Оставшаяся часть вариации успеваемости (48,26%) обусловлена другими причинами.

! Примечание: но это не является какой-то «абсолютной истиной», это всего лишь оценка в рамках построенной модели.

Очевидно, что линейный коэффициент детерминации может изменяться в пределах , и чем он ближе к единице, тем удачнее линейная модель приближает эмпирические данные.

6) Вычислим коэффициент средней эластичности

Но сначала разберёмся, что такое эластичность. Это восприимчивость. Податливость. Представьте, что уровень тревожности в обществе увеличился на 1%. А Петя стал больше тревожиться всего на 0,3%. Таким образом, Петя неэластичен к тревожности. Маша в то же время стала тревожиться больше на 5%. Таким образом, Маша эластична к тревожности.

Иными словами, эластичность  – это количество процентов, на которое изменяется признак-результат при увеличении признака-фактора на 1%. Если , то зависимый показатель неэластичен к воздействию признака-фактора. Если же  – то эластичен.

Функция эластичности имеет вид: , где  – функция регрессии, а  – её производная. И в подавляющем большинстве случаев эластичность зависит от значения , так, для линейной регрессии получаем:  – и  мы можем вычислить эластичность в той или иной точке . Но чтобы не мучиться чаще рассчитывают средний коэффициент эластичности, по формуле: .
В нашей задаче:  – таким образом, при увеличении количества прогулов на 1%  успеваемость уменьшается в среднем на 0,93%.

Можно сказать, что эластичность близкА к нейтральной – количество прогулов растёт и успеваемость падает примерно такими же темпами. Хотя, повторюсь, при различных значениях  эластичность будет разной:  – вот вам почва для дополнительного исследования. И это особенно актуально, если «икс» может принимать как положительные, так и отрицательные значения, вследствие чего среднее значение эластичности только собьёт с толку. Следует добавить, что в некоторых задачах эластичность вообще не имеет содержательного смысла, хотя чисто формально рассчитать её можно.

7) Бета-коэффициент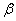  

Это ещё один относительный показатель влияния фактора на результат. «Бета» – это количество средних квадратических отклонений, на которое меняется признак-результат при увеличении признака-фактора на одно среднее квадратическое отклонение.

В чём смысл показателя? Давайте посмотрим на уравнение регрессии  и конкретно на коэффициент . Вопрос: это много или мало? (с точки зрения влияния прогулов на успеваемость). И на самом деле ответ не очевиден. Если «а» очень великО по модулю, то это ещё не значит, что влияние существенно. И наоборот, «а» может составлять какие-то «жалкие» дробные доли, но влияние окажется ого-го! Всё относительно и всё зависит от колеблемости показателей, а эта самая колеблемость измеряется стандартными отклонениями. Которые и нужно сопоставить:

 – таким образом, при увеличении количества прогулов на одно стандартное отклонение успеваемость уменьшается примерно на 0,72 своего стандартного отклонения.

Если какая-то причина сильно «надавливает» на следствие, то «бета» по модулю больше единицы , часто в разы больше. Если влияние умеренное, то . Ну а близкие к нулю значения говорят о практической невосприимчивости к фактору. В нашей задаче мы получили достаточно «сбалансированный» результат.

Задание выполнено

Но точку ставить рано. Теперь второй способ решения, в котором мы сначала находим коэффициент корреляции, а затем уравнение регрессии.

Линейный коэффициент корреляции вычислим по формуле:
, где  – стандартные отклонения признаков .

Член в числителе называют корреляционным моментом или коэффициентом ковариации (совместной вариации) признаков, он рассчитывается следующим образом: , где  – объём статистической совокупности, а  – средние значения признаков. Данный коэффициент показывает, насколько согласованно отклоняются пАрные значения  от своих средних в ту или иную сторону. Формулу можно упростить, в результате чего получится ранее использованная версия, без подробных выкладок: . Но сейчас мы пойдём другим путём.

Заполним расчётную таблицу:

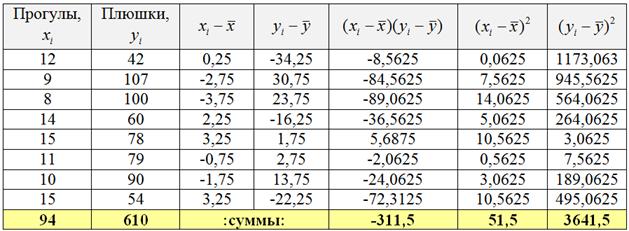
При этом сначала рассчитываем левые нижние суммы и средние значения признаков:
 и только потом заполняем оставшиеся столбцы таблицы. О том, как быстро выполнить эти вычисления в Экселе, будет видео ниже!

Вычислим коэффициент ковариации:
.

Стандартные отклонения вычислим как квадратные корни из дисперсий:

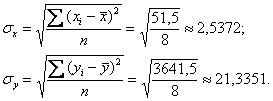
Таким образом, коэффициент корреляции:

И если нам известны значения , то коэффициенты уравнения  регрессии легко рассчитать по следующим формулам:

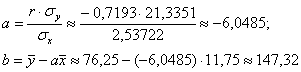
Таким образом, искомое уравнение:

Теперь смотрим ролик о том, как это всё быстро подсчитать и построить:

 Как вычислить коэффициент корреляции и найти уравнение регрессии? (Ютуб)

Если под рукой нет Экселя, ничего страшного, разобранную задачу не так трудно решить в обычной клетчатой тетради. А если Эксель есть и времени нет, то можно воспользоваться моим калькулятором. Да, вы можете найти аналоги в Сети, но, скорее всего, это будет не совсем то, что нужно ;)

Какой способ решения выбрать? Ориентируйтесь на свой учебный план и методичку. По умолчанию лучше использовать 2-й способ, он несколько короче, и, вероятно, потому и встречается чаще. Кстати, если вам нужно построить ТОЛЬКО уравнение регрессии, то уместен 1-й способ, ибо там мы находим это уравнение в первую очередь.

Следующая задача много-много лет назад была предложена курсантам местной школы милиции (тогда ещё милиции), и это чуть ли не первая задача по теме, которая встретилась в моей профессиональной карьере. И я безмерно рад предложить её вам сейчас, разумеется, с дополнительными пунктами:)

Пример 68

В результате  независимых опытов получены 7 пар чисел:

…да, числа могут быть и отрицательными.

По данным наблюдений вычислить линейный коэффициент корреляции и детерминации, сделать выводы. Найти параметры линейной регрессии  на , пояснить их смысл. Изобразить диаграмму рассеяния и график регрессии. Вычислить , что означают полученные результаты?

Из условия следует, что признак , очевидно, зависит от  (ибо кто ж делает бессвязные опыты). Однако помните, что корреляционная зависимость и причинно-следственная связь – это не одно и  то же! (прочитайте, если до сих пор не прочитали!). Поэтому, если в задаче просто предложены два числовых ряда (без контекста), то можно говорить лишь о зависимости корреляционной, но не о причинно-следственной.

Все данные уже забиты в Эксель, и вам осталось аккуратно выполнить расчёты. В образце я решил задачу вторым, более распространённым способом. И, конечно же, выполните проверку первым путём.

Следует отметить, что в целях экономии места я специально подобрал задачи с малым объёмом выборки. На практике обычно предлагают 10 или 20 пар чисел, реже 30, и максимальная выборка, которая мне встречалась в студенческих работах – 100. …Соврал малость, 80.

И сейчас я вас приглашаю на следующий урок, назову его Уравнение линейной регрессии, где мы рассчитаем и найдём всё то же самое – только для комбинационной группировки. Плюс немного глубже копнём уравнения регрессии (их два).

Решения и ответы:

Пример 68. Решение: вычислим суммы и средние значения признаков ,  и заполним расчётную таблицу:

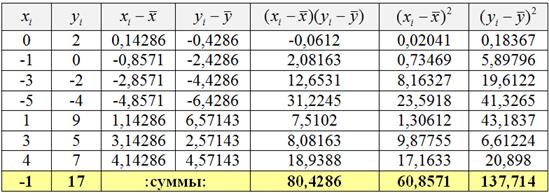
Вычислим коэффициент ковариации:
.
Вычислим средние квадратические отклонения:

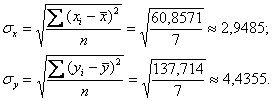
Вычислим коэффициент корреляции:
, таким образом, существует сильная прямая корреляционная зависимость  от.

Вычислим коэффициент детерминации:
 – таким образом, 77,19% вариации признака  обусловлено изменением признака . Остальная вариация (22,81%) обусловлена другими факторами.

Вычислим коэффициенты линейной регрессии :

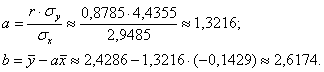
Таким образом, искомое уравнение регрессии:

Данное уравнение показывает, что с увеличением значения «икс» на одну единицу «игрек» увеличивается в среднем примерно на 1,32 единицы (смысл коэффициента «а»).

При  среднеожидаемое значение «игрек» составит примерно 2,62 ед. (смысл коэффициента «бэ»).

Найдём пару точек для построения прямой:

и выполним чертёж:

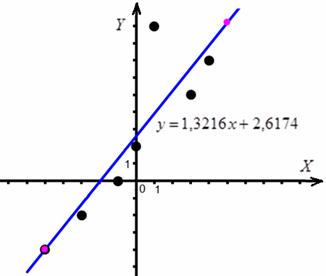
Вычислим:
 – среднеожидаемое значение «игрек» при  (интерполированный результат);
 – среднеожидаемое значение «игрек» при  (спрогнозированный результат).

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте