


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Функциональные ряды. Степенные ряды.
Область сходимости ряда
Смех без причины – признак Даламбера
Вот и пробил час функциональных рядов. Для успешного освоения темы, и, в частности, этого урока, нужно хорошо разбираться в обычных числовых рядах. Следует хорошо понимать, что такое ряд, уметь применять признаки сравнения для исследования ряда на сходимость. Таким образом, если Вы только-только приступили к изучению темы или являетесь чайником в высшей математике, необходимо последовательно проработать три урока: Ряды для чайников, Признак Даламбера. Признаки Коши и Знакочередующиеся ряды. Признак Лейбница. Обязательно все три! Если есть элементарные знания и навыки решения задач с числовыми рядами, то справиться с функциональными рядами будет довольно просто, поскольку нового материала не очень и много.
На данном уроке мы рассмотрим понятие функционального ряда (что это вообще такое), познакомимся со степенными рядами, которые встречаются в 90% практических заданий, и научимся решать распространенную типовую задачу на нахождение радиуса сходимости, интервала сходимости и области сходимости степенного ряда. Далее рекомендую рассмотреть материал о разложении функций в степенные ряды, и «скорая помощь» начинающему будет оказана. Немного отдышавшись, переходим на следующий уровень:
– к уроку о нахождении суммы степенного ряда – обратная задача к его разложению;
– к уроку о равномерной сходимости, после которого расправляемся с другими функциональными рядами.
Также в разделе функциональных рядов есть их многочисленные приложения к приближённым вычислениям, и некоторым особняком идут Ряды Фурье, которым в учебной литературе, как правило, выделяется отдельная глава. У меня всего лишь одна статья, но зато длиннющая и много-много дополнительных примеров!
Итак, ориентиры расставлены, поехали:
Понятие функционального ряда и степенного ряда
Обычный числовой ряд, вспоминаем, состоит из чисел:
![]()
Все члены ряда ![]() – это ЧИСЛА.
– это ЧИСЛА.
Функциональный же ряд состоит из ФУНКЦИЙ:
![]()
В общий член ряда ![]() помимо многочленов, факториалов и других подарков непременно входит буковка «икс». Выглядит это, например, так:
помимо многочленов, факториалов и других подарков непременно входит буковка «икс». Выглядит это, например, так: ![]() . Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
. Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
![]()
Как видите, все члены функционального ряда ![]() – это функции.
– это функции.
Наиболее популярной разновидностью функционального ряда является степенной ряд. Членами степенного ряда являются целые положительные степени переменной ![]() либо двучлена
либо двучлена ![]() , умноженные на числовые коэффициенты:
, умноженные на числовые коэффициенты:
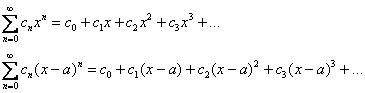
Как вы правильно догадываетесь, ![]() – это старая знакомая «начинка» числовых рядов, которая зависит только от «эн».
– это старая знакомая «начинка» числовых рядов, которая зависит только от «эн».
В практических заданиях многие степенные ряды начинаются с 1-го члена, и поэтому в своих статьях я буду часто использовать обозначения ![]() ,
, ![]() .
.
Простейшие примеры:
![]()
![]()
Следует отметить, что подобные ряды могут содержать и нулевой член (константу), в этом случае его записывают за пределами суммы. Например:
![]()
И, кроме того, степени могут «идти с пропусками»:
![]()
![]()
Это тоже степенные ряды (при желании их можно переписать с отсутствующими степенями и нулевыми коэффициентами).
Сходимость степенного ряда.
Интервал сходимости, радиус сходимости и область сходимости
Не нужно пугаться такого обилия терминов, они идут «рядом друг с другом» и не представляют особых сложностей для понимания. Лучше выберем какой-нибудь простой подопытный ряд и сразу начнём разбираться.
Прошу любить и жаловать степенной ряд ![]() .
.
Переменная ![]() может принимать любое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»:
может принимать любое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»:
Если ![]() , то
, то ![]()
Если ![]() , то
, то ![]()
Если ![]() , то
, то ![]()
Если ![]() , то
, то 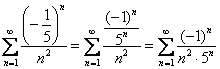
И так далее.
Очевидно, что, подставляя в ![]() то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд
то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд ![]() будет сходиться. Такое множество и называется областью сходимости ряда.
будет сходиться. Такое множество и называется областью сходимости ряда.
Для любого степенного ряда (временно отвлекаемся от конкретного примера) возможны три случая:
1) Степенной ряд сходится абсолютно на некотором интервале ![]() . Иными словами, если мы выбираем любое значение «икс» из интервала
. Иными словами, если мы выбираем любое значение «икс» из интервала ![]() и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал
и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал ![]() и называется интервалом сходимости степенного ряда.
и называется интервалом сходимости степенного ряда.
Радиус сходимости, если совсем просто, это половина длины интервала сходимости:
![]()
Геометрически ситуация выглядит так:
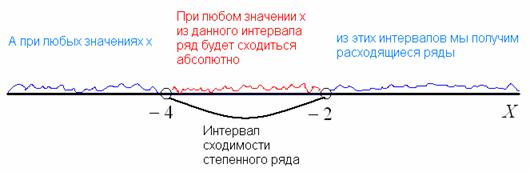
В данном случае, интервал сходимости ряда: ![]() , радиус сходимости ряда:
, радиус сходимости ряда: ![]()
Широко распространен тривиальный случай, когда интервал сходимости симметричен относительно нуля:
 >
>
Здесь интервал сходимости ряда: ![]() , радиус сходимости ряда:
, радиус сходимости ряда: ![]()
А что будет происходить на концах интервала ![]() ? В точках
? В точках ![]() ,
, ![]() степенной ряд может как сходиться, так и расходиться, и для выяснения этого нужно проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
степенной ряд может как сходиться, так и расходиться, и для выяснения этого нужно проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости: ![]()
– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости ряда представляет собой полуинтервал: ![]() или
или ![]() .
.
– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок: ![]()
Термины очень похожи, область сходимости ряда – это чуть более детализированный интервал сходимости ряда.
С двумя оставшимися случаями всё короче и проще:
2) Степенной ряд сходится абсолютно при любом значении ![]() . То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают:
. То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: ![]() . Радиус сходимости:
. Радиус сходимости: ![]() . Рисунок приводить не буду, думаю, нет необходимости.
. Рисунок приводить не буду, думаю, нет необходимости.
3) Степенной ряд сходится в единственной точке. Если ряд имеет вид ![]() , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке ![]() . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:
. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: ![]() . Если ряд имеет вид
. Если ряд имеет вид ![]() , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке ![]() , если ряд имеет вид
, если ряд имеет вид ![]() , то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой:
, то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой: ![]() .
.
Других вариантов нет. Область сходимости степенного ряда – это всегда либо единственная точка, либо любое «икс», либо интервал ![]() (возможно полуинтервал, отрезок). Подчеркиваю, что данная классификация справедлива для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.
(возможно полуинтервал, отрезок). Подчеркиваю, что данная классификация справедлива для степенных рядов. Для произвольного функционального ряда она в общем случае является неверной.
Исследование степенного ряда на сходимость
После небольшой порции теоретического материала переходим к рассмотрению типового задания, которое практически всегда встречается на зачетах и экзаменах по высшей математике.
Пример 1
Найти область сходимости степенного ряда ![]()
Задание часто формулируют эквивалентно: Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала.
Алгоритм решения довольно прозрачен и трафаретен.
На первом этапе находим интервал сходимости ряда. В большинстве заданий используется схема, основанная на признаке Даламбера для произвольных числовых рядов (на сайте освещен лишь косвенно). Технически нам нужно вычислить предел 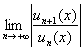 , и с формальной техникой его решения вы уже бОльшей частью знакомы:
, и с формальной техникой его решения вы уже бОльшей частью знакомы:
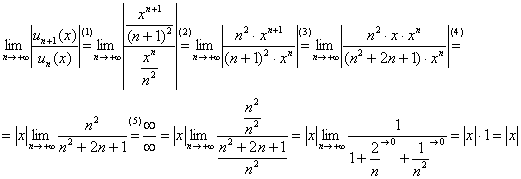
(1) Составляем отношение следующего члена ряда к предыдущему.
(2) Избавляемся от четырехэтажности дроби.
(3) В числителе по правилу действий со степенями «отщипываем» один «икс». В знаменателе возводим двучлен в квадрат.
(4) Выносим оставшийся «икс» за знак предела, причем, выносим его вместе со знаком модуля. Почему со знаком модуля? Дело в том, что наш предел ![]() и так будет неотрицательным, а вот «икс» вполне может принимать отрицательные значения. Поэтому модуль относится именно к нему.
и так будет неотрицательным, а вот «икс» вполне может принимать отрицательные значения. Поэтому модуль относится именно к нему.
Кстати, почему ![]() можно вообще вынести за знак предела? Потому что «динамической» переменной в пределе у нас является «эн», и от этого нашему «иксу» ни жарко ни холодно.
можно вообще вынести за знак предела? Потому что «динамической» переменной в пределе у нас является «эн», и от этого нашему «иксу» ни жарко ни холодно.
(5) Устраняем неопределенность ![]() стандартным способом.
стандартным способом.
После того, как предел найден, нужно проанализировать, что у нас получилось. Внимание! Вычисленный предел и интерпретацию его результатов (см. ниже) НЕЛЬЗЯ считать или называть «признаком Даламбера». Подчеркну ещё раз, что рассматриваемая схема лишь основана (не вдаюсь в подробности) на признаке Даламбера для числовых рядов.
Итак:
Если в пределе получается ноль, то алгоритм решения заканчивает свою работу, и мы даём окончательный ответ задания: «Область сходимости степенного ряда: ![]() » (любое действительное число – случай №2 предыдущего параграфа). То есть, степенной ряд сходится при любом значении «икс». Ответ можно записать эквивалентно: «Ряд сходится при
» (любое действительное число – случай №2 предыдущего параграфа). То есть, степенной ряд сходится при любом значении «икс». Ответ можно записать эквивалентно: «Ряд сходится при ![]() » (значок
» (значок ![]() в математике обозначает принадлежность).
в математике обозначает принадлежность).
Если в пределе получается бесконечность, то алгоритм решения также заканчивает свою работу, и мы даём окончательный ответ задания: «Ряд сходится при ![]() » (или при
» (или при ![]() либо
либо ![]() »). Смотрите случай №3 предыдущего параграфа.
»). Смотрите случай №3 предыдущего параграфа.
Если в пределе получается не ноль и не бесконечность, то у нас самый распространенный на практике случай №1 – ряд сходится на некотором интервале.
В данном случае предел равен ![]() . Как найти интервал сходимости ряда? Составляем неравенство:
. Как найти интервал сходимости ряда? Составляем неравенство:
![]()
В ЛЮБОМ задании данного типа в левой части неравенства должен находиться результат вычисления предела, а в правой части неравенства – строго единица. Не буду объяснять, почему именно такое неравенство и почему справа единица. Уроки носят практическую направленность, и уже очень хорошо, что от моих рассказов не повесился профессорско-преподавательский состав стали понятнее некоторые теоремы.
Техника работы с модулем и решения двойных неравенств подробно рассматривалась на первом курсе в статье Область определения функции, но для удобства я постараюсь максимально подробно закомментировать все действия. Раскрываем неравенство с модулем по школьному правилу ![]() . В данном случае:
. В данном случае:
![]() – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Половина пути позади.
На втором этапе необходимо исследовать сходимость ряда на концах найденного интервала.
Сначала берём левый конец интервала ![]() и подставляем его в наш степенной ряд
и подставляем его в наш степенной ряд ![]() :
:
При ![]()
Получен числовой ряд, и нам нужно исследовать его на сходимость (уже знакомая из предыдущих уроков задача).
Используем признак Лейбница:
1) Ряд является знакочередующимся.
2) ![]() – члены ряда убывают по модулю. При этом каждый следующий член ряда по модулю меньше предыдущего:
– члены ряда убывают по модулю. При этом каждый следующий член ряда по модулю меньше предыдущего: ![]() , значит, убывание монотонно.
, значит, убывание монотонно.
Вывод: ряд сходится.
С помощью ряда, составленного из модулей, выясним, как именно:
![]() – сходится («эталонный» ряд из семейства обобщенного гармонического ряда).
– сходится («эталонный» ряд из семейства обобщенного гармонического ряда).
Таким образом, полученный числовой ряд сходится абсолютно.
Далее рассматриваем правый конец интервала ![]() , подставляем это значение в наш степенной ряд
, подставляем это значение в наш степенной ряд ![]() :
:
при ![]() – сходится.
– сходится.
! Напоминаю, что любой сходящийся положительный ряд тоже является абсолютно сходящимся.
Таким образом, степенной ряд ![]() сходится, причём абсолютно, на обоих концах найденного интервала.
сходится, причём абсолютно, на обоих концах найденного интервала.
Ответ: область сходимости исследуемого степенного ряда: ![]()
Имеет право на жизнь и другое оформление ответа: Ряд сходится, если ![]()
Иногда в условии задачи требуют указать радиус сходимости. Очевидно, что в рассмотренном примере ![]() .
.
Пример 2
Найти область сходимости степенного ряда ![]()
Решение: интервал сходимости ряда найдём с помощью признака Даламбера (но не ПО признаку! – для функциональных рядов такого признака не существует):
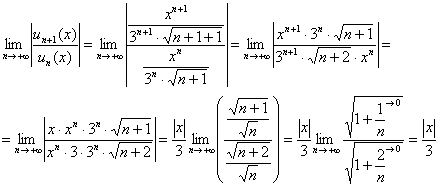
Составляем стандартное неравенство:
Ряд сходится при ![]()
Слева нам нужно оставить только ![]() , поэтому умножаем обе части неравенства на 3:
, поэтому умножаем обе части неравенства на 3:
![]()
И раскрываем неравенство с модулем по правилу ![]() :
:
![]() – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала:
1) При ![]()
Обратите внимание, что при подстановке значения ![]() в степенной ряд
в степенной ряд ![]() у нас сократились
у нас сократились ![]() . Это верный признак того, что мы правильно нашли интервал сходимости ряда.
. Это верный признак того, что мы правильно нашли интервал сходимости ряда.
Исследуем полученный числовой ряд на сходимость.
Используем признак Лейбница:
– Ряд является знакочередующимся.
– ![]() – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше предыдущего:
– члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше предыдущего: ![]() , значит, убывание монотонно.
, значит, убывание монотонно.
Вывод: ряд сходится.
Исследуем его на характер сходимости:
![]()
Сравним данный ряд с расходящимся рядом ![]() .
.
Используем предельный признак сравнения:
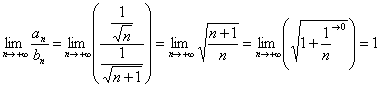
Получено конечное число, отличное от нуля, значит, ряд ![]() расходится вместе с рядом
расходится вместе с рядом ![]() .
.
Таким образом, ряд ![]() сходится условно.
сходится условно.
2) При ![]() – расходится (по доказанному).
– расходится (по доказанному).
Ответ: Область сходимости исследуемого степенного ряда: ![]() . При
. При ![]() ряд сходится условно.
ряд сходится условно.
В рассмотренном примере областью сходимости степенного ряда является полуинтервал, причем во всех точках интервала ![]() степенной ряд сходится абсолютно, а в точке
степенной ряд сходится абсолютно, а в точке ![]() , как выяснилось – условно.
, как выяснилось – условно.
Пример 3
Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала ![]()
Это пример для самостоятельного решения.
Рассмотрим пару примеров, которые встречаются редко, но встречаются.
Пример 4
Найти область сходимости ряда: ![]()
Решение: с помощью признака Даламбера найдем интервал сходимости данного ряда:
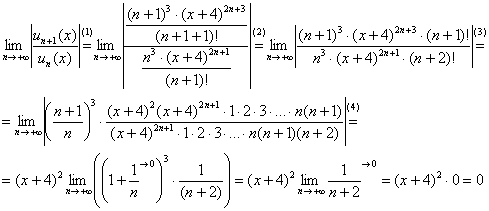
(1) Составляем отношение следующего члена ряда к предыдущему.
(2) Избавляемся от четырехэтажности дроби.
(3) Кубы ![]() и
и ![]() по правилу действий со степенями подводим под единую степень. В числителе хитро раскладываем степень
по правилу действий со степенями подводим под единую степень. В числителе хитро раскладываем степень ![]() , т.е. раскладываем таким образом, чтобы на следующем шаге сократить дробь на
, т.е. раскладываем таким образом, чтобы на следующем шаге сократить дробь на ![]() . Факториалы расписываем подробно.
. Факториалы расписываем подробно.
(4) Под кубом почленно делим числитель на знаменатель, указывая, что ![]() . В дроби сокращаем всё, что можно сократить. Множитель
. В дроби сокращаем всё, что можно сократить. Множитель ![]() выносим за знак предела, его можно вынести, поскольку в нём нет ничего, зависящего от «динамической» переменной «эн». Обратите внимание, что знак модуля не нарисован – по той причине, что
выносим за знак предела, его можно вынести, поскольку в нём нет ничего, зависящего от «динамической» переменной «эн». Обратите внимание, что знак модуля не нарисован – по той причине, что ![]() принимает неотрицательные значения при любом «икс».
принимает неотрицательные значения при любом «икс».
В пределе получен ноль, а значит, можно давать окончательный ответ:
Ответ: Ряд сходится при ![]()
А сначала-то казалось, что этот ряд со «страшной начинкой» будет трудно решить. Ноль или бесконечность в пределе – почти подарок, ведь решение заметно сокращается!
Пример 5
Найти область сходимости ряда ![]()
Это пример для самостоятельного решения. Будьте внимательны ;-) Полное решение ответ в конце урока.
Рассмотрим еще несколько примеров, содержащих элемент новизны в плане использования технических приемов.
Пример 6
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала ![]()
Решение: В общий член степенного ряда входит множитель ![]() , обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении предела
, обеспечивающий знакочередование. Алгоритм решения полностью сохраняется, но при составлении предела 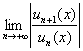 мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».
мы игнорируем (не пишем) этот множитель, поскольку модуль уничтожает все «минусы».
Интервал сходимости ряда найдём с помощью признака Даламбера:

Составляем стандартное неравенство:
Ряд сходится при ![]()
Слева нам нужно оставить только модуль, поэтому умножаем обе части неравенства на 5:
![]()
Теперь раскрываем модуль уже знакомым способом:
![]()
В середине двойного неравенства нужно оставить только «икс», в этих целях из каждой части неравенства вычитаем 2:
![]()
![]() – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) Подставляем значение ![]() в наш степенной ряд
в наш степенной ряд ![]() :
:

Будьте предельно внимательны, множитель ![]() не обеспечивает знакочередование, при любом натуральном «эн»
не обеспечивает знакочередование, при любом натуральном «эн» ![]() . Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда.
. Полученный минус выносим за пределы ряда и забываем про него, поскольку он (как и любая константа-множитель) никак не влияет на сходимость или расходимость числового ряда.
Еще раз заметьте, что в ходе подстановки значения ![]() в общий член степенного ряда у нас сократился множитель
в общий член степенного ряда у нас сократился множитель ![]() . Если бы этого не произошло, то это бы значило, что мы либо неверно вычислили предел, либо неправильно раскрыли модуль.
. Если бы этого не произошло, то это бы значило, что мы либо неверно вычислили предел, либо неправильно раскрыли модуль.
Итак, требуется исследовать на сходимость числовой ряд ![]() . Здесь проще всего использовать предельный признак сравнения и сравнить данный ряд с расходящимся гармоническим рядом. Но, если честно, предельный признак сравнения до ужаса мне надоел, поэтому внесу некоторое разнообразие в решение.
. Здесь проще всего использовать предельный признак сравнения и сравнить данный ряд с расходящимся гармоническим рядом. Но, если честно, предельный признак сравнения до ужаса мне надоел, поэтому внесу некоторое разнообразие в решение.
Используем интегральный признак:
![]()
Подынтегральная функция непрерывна на ![]() .
.
![]()
Таким образом, полученный числовой ряд расходится вместе с соответствующим несобственным интегралом.
2) Исследуем второй конец интервала сходимости.
При ![]()
Используем признак Лейбница:
– Ряд является знакочередующимся.
– ![]() – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий:
– члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий: ![]() , значит, убывание монотонно.
, значит, убывание монотонно.
Вывод: ряд сходится
Полученный числовой ряд не является абсолютно сходящимся поскольку ![]() – расходится (по доказанному).
– расходится (по доказанному).
Ответ: ![]() – область сходимости исследуемого степенного ряда, при
– область сходимости исследуемого степенного ряда, при ![]() ряд сходится условно.
ряд сходится условно.
Пример 7
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала ![]()
Это пример для самостоятельного решения.
Кто утомился, может сходить покурить, а мы рассмотрим еще два примера.
Пример 8
Найти интервал сходимости ряда и исследовать его сходимость на концах найденного интервала ![]()
Решение: Найдем интервал сходимости ряда:
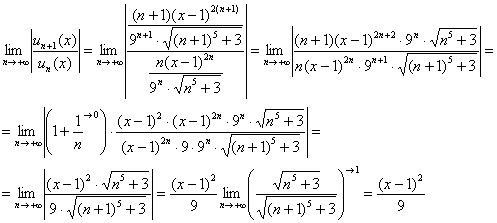
Предел 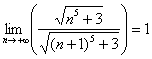 по той причине, что числитель и знаменатель одного порядка роста. Более подробно об этом моменте и «турбо»-методе решения читайте в статье о признаке Даламбера.
по той причине, что числитель и знаменатель одного порядка роста. Более подробно об этом моменте и «турбо»-методе решения читайте в статье о признаке Даламбера.
Итак, ряд сходится при ![]()
Умножаем обе части неравенства на 9:
![]()
Извлекаем из обеих частей корень, при этом помним старый школьный прикол ![]() :
:
![]()
![]()
Раскрываем модуль:
![]()
и прибавляем ко всем частям единицу:
![]()
![]() – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала:
1) Если ![]() , то получается следующий числовой ряд:
, то получается следующий числовой ряд:

Множитель ![]() бесследно пропал, поскольку при любом натуральном значении «эн»
бесследно пропал, поскольку при любом натуральном значении «эн» ![]() .
.
И в третий раз обращаю внимание на то, что в результате подстановки сократились ![]() , а значит, интервал сходимости найден правильно.
, а значит, интервал сходимости найден правильно.
По всем признакам для полученного числового ряда ![]() следует применить предельный признак сравнения. Какой ряд подобрать для сравнения? Об этой методике я уже рассказывал в соответствующем параграфе. Повторим.
следует применить предельный признак сравнения. Какой ряд подобрать для сравнения? Об этой методике я уже рассказывал в соответствующем параграфе. Повторим.
Определяем старшую степень знаменателя, для этого мысленно или на черновике отбрасываем под корнем всё, кроме самого старшего слагаемого: ![]() . Таким образом, старшая степень знаменателя равна
. Таким образом, старшая степень знаменателя равна ![]() . Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя:
. Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя: ![]() .
.
Таким образом, наш ряд нужно сравнить со сходящимся рядом 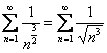 .
.
Используем предельный признак сравнения:
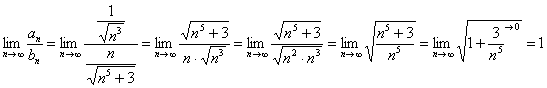
Получено конечное, отличное от нуля число, значит, ряд ![]() сходится вместе с рядом
сходится вместе с рядом ![]() .
.
2) Что происходит на другом конце интервала?
При ![]() – а вот и вознаграждение за мучения в предыдущем пункте! Получился точно такой же числовой ряд, сходимость которого мы только что доказали.
– а вот и вознаграждение за мучения в предыдущем пункте! Получился точно такой же числовой ряд, сходимость которого мы только что доказали.
Ответ: область сходимости исследуемого степенного ряда: ![]()
Чуть менее сложный пример для самостоятельного решения:
Пример 9
Найти область сходимости ряда ![]()
Достаточно для начала =)
В заключение остановлюсь на одном моменте. Во всех примерах мы опирались на признак Даламбера и составляли предел 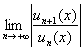 . Но всегда ли нужно делать именно так? Почти всегда. Однако в некоторых случаях бывает невероятно выгодно привлечь на помощь радикальный признак Коши и составить предел
. Но всегда ли нужно делать именно так? Почти всегда. Однако в некоторых случаях бывает невероятно выгодно привлечь на помощь радикальный признак Коши и составить предел ![]() , при этом алгоритм решения задачи остаётся прежним! Что это за случаи? Это те случаи, когда из общего члена степенного ряда «хорошо» (полностью) извлекается корень «энной» степени, и такие примеры я разберу в статье о равномерной сходимости ряда.
, при этом алгоритм решения задачи остаётся прежним! Что это за случаи? Это те случаи, когда из общего члена степенного ряда «хорошо» (полностью) извлекается корень «энной» степени, и такие примеры я разберу в статье о равномерной сходимости ряда.
Но «чайникам» с равномерной сходимостью лучше не спешить – сначала целесообразно изучить второй урок начального уровня – Разложение функций в степенные ряды. Примеры решений.
Желаю успехов!
Решения и ответы:
Пример 3: Решение: интервал сходимости ряда найдём с помощью признака Даламбера:
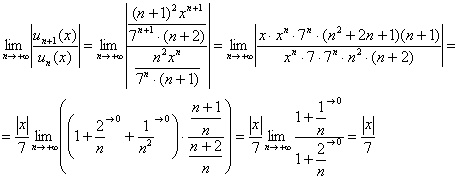
Ряд сходится при ![]()
Слева нужно оставить только модуль, поэтому умножаем обе части неравенства на 7:
![]()
![]() – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) При ![]()
Проверяем выполнение условий признака Лейбница:
– ряд является знакочередующимся;
– 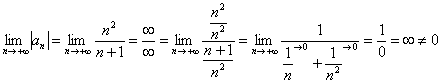 – члены ряда не убывают по модулю, следовательно, предела
– члены ряда не убывают по модулю, следовательно, предела ![]() . не существует.
. не существует.
Вывод: ряд расходится, т.к. не выполнен необходимый признак сходимости ряда.
2) При ![]() – расходится по той же причине.
– расходится по той же причине.
Ответ: ![]() – область сходимости исследуемого степенного ряда
– область сходимости исследуемого степенного ряда
Пример 5: Решение: с помощью признака Даламбера найдём интервал сходимости:
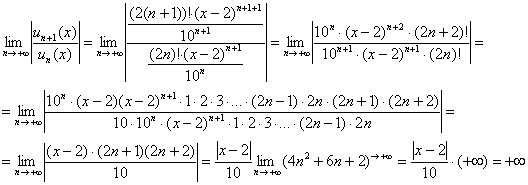
Ответ: Ряд сходится при ![]()
Пример 7: Решение: найдем интервал сходимости данного степенного ряда:

Ряд сходится при ![]()
Слева нужно оставить только модуль, умножаем обе части неравенства на ![]() :
:
![]()
![]()
В середине нужно оставить только «икс», вычитаем из каждой части неравенства 3:
![]()
![]() – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
1) При 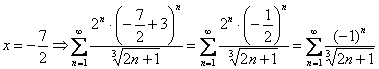
Примечание: множитель ![]() сократился, значит, мы на верном пути.
сократился, значит, мы на верном пути.
Используем признак Лейбница:
Ряд является знакочередующимся;
![]() – члены ряда убывают по модулю;
– члены ряда убывают по модулю;
каждый следующий член ряда по модулю меньше, чем предыдущий: ![]() , значит, убывание монотонно.
, значит, убывание монотонно.
Таким образом, ряд сходится по признаку Лейбница.
Исследуем его на абсолютную/условную сходимость:
![]()
Используем интегральный признак:
![]()
Подынтегральная функция непрерывна на ![]() .
.
![]()
Таким образом, ряд ![]() расходится вместе с соответствующим несобственным интегралом.
расходится вместе с соответствующим несобственным интегралом.
Примечание: здесь можно было использовать и предельный признак сравнения.
Вывод: ряд ![]() сходится условно.
сходится условно.
2) При  – расходится (по доказанному).
– расходится (по доказанному).
Ответ: Область сходимости исследуемого степенного ряда: ![]() , при
, при ![]() ряд сходится условно.
ряд сходится условно.
Область сходимости окончательно можно записать так: ![]() , или даже так:
, или даже так: ![]() . Но не нужно :) ;).
. Но не нужно :) ;).
Пример 9: Решение: Найдем интервал сходимости ряда:
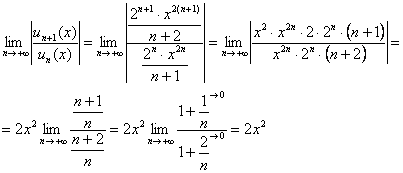
Ряд сходится при ![]()
![]()
![]()
![]() – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала.
1) При 
Сравним данный ряд с расходящимся гармоническим рядом ![]() . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
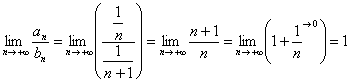
Получено конечное число, отличное от нуля, значит, полученный числовой ряд расходится вместе с гармоническим рядом.
2) При  – расходится (по доказанному).
– расходится (по доказанному).
Ответ: область сходимости исследуемого степенного ряда: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright