Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Дисперсия дискретной случайной величины.
Среднее квадратическое отклонение

Итак, продолжаем. В предыдущей статье мы выяснили, насколько полезно знать математическое ожидание, однако только этой характеристики ещё не достаточно для исследования случайной величины. Представим двух стрелков, которые стреляют по мишени. Один стреляет метко и попадает близко к центру, а другой… просто развлекается и даже не целится. Но что забавно, его средний результат будет точно таким же, как и у первого стрелка! Эту ситуацию условно иллюстрируют следующие случайные величины:

«Снайперское» математическое ожидание равно , однако и у «интересной личности»:  – оно тоже нулевое!

Таким образом, возникает потребность количественно оценить, насколько далеко  рассеяны пули (значения случайной величины) относительно центра мишени (математического ожидания). Ну а рассеяние с латыни переводится не иначе, как дисперсия.

Посмотрим, как определяется эта числовая характеристика на одном из примеров 1-й части урока:

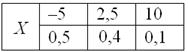
Там мы нашли неутешительное математическое ожидание  этой игры, и сейчас нам предстоит вычислить её дисперсию, которая обозначается через .

Выясним, насколько далеко «разбросаны» выигрыши/проигрыши относительно среднего значения. Очевидно, что для этого нужно вычислить разности  между значениями случайной величины и её математическим ожиданием:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Теперь вроде бы нужно просуммировать результаты, но этот путь не годится – по той причине, что колебания влево будут взаимоуничтожаться с колебаниями вправо. Так, например, у стрелка-«любителя» (пример выше) разности составят ,  и при сложении дадут ноль, поэтому никакой оценки рассеяния его стрельбы мы не получим.

Чтобы обойти эту неприятность можно рассмотреть модули разностей, но по техническим причинам прижился подход, когда их возводят в квадрат. Решение удобнее оформить таблицей:

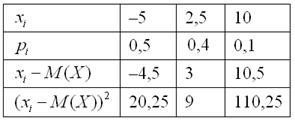
И здесь напрашивается вычислить средневзвешенное значение квадратов отклонений. А это ЧТО такое? Это их математическое ожидание, которое и является мерилом рассеяния:

  – определение дисперсии. Из определения сразу понятно, что дисперсия не может быть отрицательной – возьмите на заметку для практики!

Вспоминаем, как находить матожидание. Перемножаем квадраты разностей на соответствующие вероятности (продолжение таблицы):
 – образно говоря, это «сила тяги»,
и суммируем результаты:

Не кажется ли вам, что на фоне выигрышей  результат получился великоватым? Всё верно – мы возводили в квадрат, и чтобы вернуться в размерность нашей игры, нужно извлечь квадратный корень. Данная величина называется средним квадратическим отклонением и обозначается греческой буквой «сигма»:

Иногда это значение называют стандартным отклонением.

В чём его смысл? Если мы отклонимся от математического ожидания  влево и вправо на среднее квадратическое отклонение:

 – то на этом интервале будут «сконцентрированы» наиболее вероятные значения случайной величины. Что мы, собственно, и наблюдаем:

Однако так сложилось, что при анализе рассеяния почти всегда оперируют понятием дисперсии. Давайте разберёмся, что она означает применительно к играм. Если в случае со стрелками речь идёт о «кучности» попаданий относительно центра мишени, то здесь дисперсия характеризует две вещи:

Во-первых, очевидно то, что при увеличении ставок, дисперсия тоже возрастает. Так, например, если мы увеличим  в 10 раз, то математическое ожидание увеличится в 10 раз, а дисперсия – в 100 раз (коль скоро, это квадратичная величина). Но, заметьте, что сами-то правила игры не изменились! Изменились лишь ставки, грубо говоря, раньше мы ставили 10 рублей, теперь 100.

Второй, более интересный момент состоит в том, что дисперсия характеризует стиль игры. Мысленно зафиксируем игровые ставки на каком-то определённом уровне, и посмотрим, что здесь к чему:

Игра с низкой дисперсией – это осторожная игра. Игрок склонен выбирать самые надёжные схемы, и в ситуации неопределённости не ставит слишком большие деньги. Например, система «красное/чёрное» в рулетке (см. Пример 4 статьи Случайные величины).

Игра с высокой дисперсией. Её часто называют дисперсионной игрой. Это авантюрный или агрессивный стиль игры, где игрок выбирает «адреналиновые» схемы. Вспомним хотя бы  «Мартингейл», в котором на кону оказываются суммы, на порядки превосходящие «тихую» игру предыдущего пункта.

Показательна ситуация в покере: здесь есть так называемые тайтовые игроки, которые склонны осторожничать и «трястись» над своими игровыми средствами (банкроллом). Неудивительно, что их банкролл не подвергается значительным колебаниям (низкая дисперсия). Наоборот, если у игрока высокая дисперсия, то это агрессор. Он часто рискует, делает крупные ставки и может, как сорвать огромный банк, так и програться в пух и прах .

То же самое происходит на Форексе, других биржах и так далее – примеров масса.

Причём, во всех случаях не важно – на копейки ли идёт игра или на тысячи долларов. На любом уровне есть свои низко- и высокодисперсионные игроки. Ну а за средний выигрыш, как мы помним, «отвечает» математическое ожидание.

Наверное, вы заметили, что нахождение дисперсии – есть процесс длительный и кропотливый. Но математика щедрА:

Формула для нахождения дисперсии

Данная формула выводится непосредственно из определения дисперсии, и мы незамедлительно пускаем её в оборот. Скопирую сверху табличку с нашей игрой:

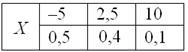
и найденное матожидание .

Вычислим дисперсию вторым способом. Сначала найдём математическое ожидание  – квадрата случайной величины . По определению математического ожидания:

В данном случае:

Таким образом, по формуле:

Как говорится, почувствуйте разницу. И на практике, конечно, лучше применять формулу (если иного не требует условие).

Осваиваем технику решения и оформления:

Пример 6

Дискретная случайная величина задана своим законом распределения:

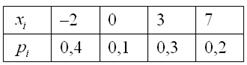
Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.

Эта задача встречается повсеместно, и, как правило, идёт без содержательного смысла.
Можете представлять себе несколько лампочек с числами, которые загораются в дурдоме с определёнными вероятностями :)

Решение: Основные вычисления удобно свести в таблицу. Сначала в  верхние две строки записываем исходные данные. Затем рассчитываем произведения , затем  и, наконец, суммы в правом столбце:

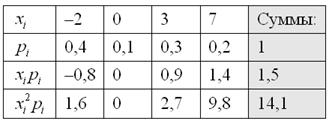
Собственно, почти всё готово. В третьей строке нарисовалось готовенькое математическое ожидание: .

Дисперсию вычислим по формуле:

И, наконец, среднее квадратическое отклонение:
 – лично я обычно округляю до 2 знаков после запятой.

Все вычисления можно провести на калькуляторе, а ещё лучше – в Экселе:

вот здесь уже трудно ошибиться :)

Ответ:

Желающие могут ещё более упростить свою жизнь и воспользоваться моим калькулятором (демо), который не только моментально решит данную задачу, но и построит тематические графики (скоро дойдём). Программа доступна за символическую плaтy. Спасибо за поддержку проекта!

Пара заданий для самостоятельного решения:

Пример 7

Вычислить дисперсию случайной величины  предыдущего примера по определению.

И аналогичный пример:

Пример 8

Дискретная случайная величина задана своим законом распределения:

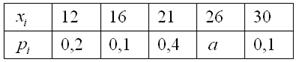
Найти

Да, значения случайной величины бывают достаточно большими (пример из реальной работы), и здесь по возможности используйте Эксель. Как, кстати, и в Примере 7 – это быстрее, надёжнее и приятнее.

Решения и ответы внизу страницы.

В заключение 2-й части урока разберём ещё одну типовую задачу, можно даже сказать, небольшой ребус:

Пример 9

Дискретная случайная величина  может принимать только два значения:  и , причём . Известна вероятность , математическое ожидание  и дисперсия .

Найти .

Решение: начнём с неизвестной вероятности. Так как случайная величина может принять только два значения, то сумма вероятностей соответствующих событий:

и поскольку , то .

Осталось найти …, легко сказать :) Но да ладно, понеслось. По определению математического ожидания:
 – подставляем известные величины:

 – и больше из этого уравнения ничего не выжать, разве что можно переписать его в привычном направлении:

ОК, едем дальше. По формуле вычисления дисперсии:
 – подставляем известные данные:

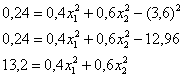
или:

О дальнейших действиях, думаю, вы догадываетесь. Составим и решим систему:

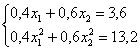
Десятичные дроби – это, конечно, полное безобразие; умножаем оба уравнения на 10:

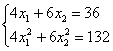
и делим на 2:

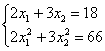
Вот так-то лучше. Из 1-го уравнения выражаем:
 (это более простой путь) – подставляем во 2-е уравнение:

Возводим в квадрат и проводим упрощения:

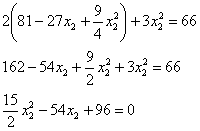
Умножаем на :

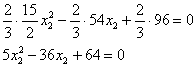
В результате получено квадратное уравнение, находим его дискриминант:
  – отлично!

и у нас получается два решения:

1) если , то ;

2) если , то .

Условию  удовлетворяет первая пара значений. С высокой вероятностью всё правильно, но, тем не менее, запишем закон распределения:

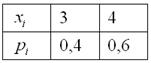
и выполним проверку, а именно, найдём матожидание:

и дисперсию:

В результате получены исходные значения, что и требовалось проверить.

Ответ:

Следует отметить, что это технически трудное задание, и поэтому в нём следует проявлять повышенное внимание. Потренируйтесь самостоятельно:

Пример 10

Случайная величина  принимает только два значения:  и , причём . Найти эти значения, если .

Тут вычисления попроще.

Жду вас в третьей, заключительной части урока, где мы познакомимся с многоугольником и функцией распределения. Её лучше изучить как можно скорее!

Решения и ответы:

Пример 7. Решение: вычислим математическое ожидание:

Вычислим дисперсию по определению:
Заполним расчётную таблицу:

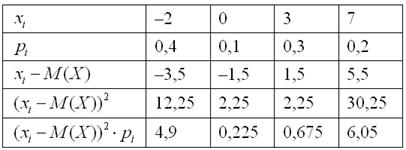
Таким образом:

Ответ:

Пример 8. Решение: случайная величина может принять только 5 значений, поэтому:

Заполним расчётную таблицу:

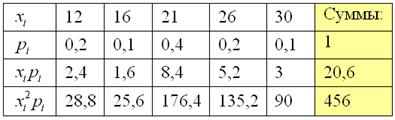
Математическое ожидание: .
Дисперсию вычислим по формуле:

Среднее квадратическое отклонение:
 

Ответ:

Пример 10. Решение: т.к. случайная величина  может принимать только 2 значения, то:
.
По определению математического ожидания:

По формуле вычисления дисперсии:

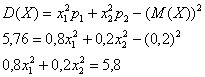
Составим и решим систему:

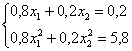
Умножим оба уравнения на 5:

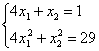
Из первого уравнения выразим:  – подставим во второе:

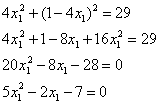
Решим полученное квадратное уравнение:

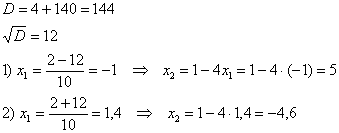
Условию  удовлетворяет первая пара.

Ответ:

Проверка:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте