Зависимые и независимые случайные величины.
Условные законы распределения и ковариация дискретных СВ

На первом уроке по теме уже фигурировали задачи с независимыми случайными величинами, и давайте сразу вспомним, что это значит: случайные величины являются независимыми, если закон распределения вероятностей любой из них, не зависит от того, какие значения приняли (или примут) остальные случайные величины.

Например, система двух игральных кубиков – совершенно понятно, что результат броска одного кубика никак не влияет на вероятности выпадения граней другого кубика. Или одинаковые независимо работающие игровые автоматы. И, наверное, у некоторых сложилось впечатление, что независимы вообще любые СВ. Однако это далеко не всегда так.

Рассмотрим одновременное сбрасывание двух кубиков-магнитов, у которых северные полюса находятся на стороне 1-очковой грани и южные – на противоположной грани в 6 очков. Будут ли независимыми аналогичные случайные величины? Да, будут. Просто снизятся вероятности выпадения «1» и «6» и увеличатся шансы других граней, т. к. в результате испытания кубики могут притянуться противоположными полюсами.

Теперь рассмотрим систему , в которой кубики сбрасываются последовательно:

– количество очков, выпавших на первом кубике;

– количество очков, выпавших на втором кубике, при условии, что он всё время сбрасывается по правую (например) сторону от 1-го кубика.

В этом случае закон распределения случайной величины зависит от того, как расположился 1-й кубик. Вторая кость может либо притянуться, либо наоборот – отскочить (если «встретились» одноимённые полюса), либо частично или полностью проигнорировать 1-й кубик.

Второй пример: предположим, что одинаковых игровых автоматов объединены в единую сеть, и – есть система случайных величин - выигрышей на соответствующих автоматах. Не знаю, законна ли эта схема, но владелец игрового зала вполне может настроить сеть следующим образом: при выпадении крупного выигрыша на каком-либо автомате, автоматически меняются законы распределения выигрышей вообще на всех автоматах. В частности, целесообразно на некоторое время обнулить вероятности крупных выигрышей, чтобы заведение не столкнулось с нехваткой средств (в том случае, если вдруг кто-то выиграет по-крупному ещё раз). Таким образом, рассмотренная система будет зависима.

То были примеры с дискретными случайными величинами. Но, разумеется, существуют и дву- и большемерные непрерывные случайные величины. Пример третий, баян:

– рост наугад выбранного человека;

– его вес.

И для наглядности представим две группы людей: ростом 160 и 190 см. Совершенно понятно, что во 2-й группе окажутся преимущественно более тяжелые люди, нежели в 1-й. То есть распределение случайной величины зависит от того, какое значение приняла случайная величина , и поэтому система зависима. В отличие от жёсткой функциональной зависимости (а-ля ) здесь имеет место вероятностная, или как говорят, стохастическая зависимость. Это проявляется в том, что, выбрав наугад человека невысокого (например) роста, более вероятно столкнуться со «стандартным» весом таких людей, но всё же существует вероятность, что у него окажется очень большой либо очень маленький вес для своей «ростовой категории».

Как составить закон распределения системы зависимых СВ? Для независимых дискретных систем мы использовали теорему умножения вероятностей независимых событий, и Капитан Очевидность подсказывает, что сейчас нужно применить аналогичную теорему для зависимых событий.

В качестве демонстрационного примера рассмотрим колоду из 8 карт, пусть это будут короли и дамы, и простую игру, в которой два игрока последовательно (не важно, в каком порядке) извлекают из колоды по одной карте. Рассмотрим случайную величину , которая символизирует одного игрока и принимает следующие значения: 1, если он извлёк червовую карту, и 0 – если карту другой масти.

Аналогично, пусть случайная величина символизирует другого игрока и тоже принимает значения 0 либо 1, если он извлёк не черву и черву соответственно.

По теореме умножения вероятностей зависимых событий:

– вероятность того, что оба игрока извлекут черву,

– вероятность того, что оба извлекут не черву, и:

– вероятность того, что один извлечёт черву, а другой – нет; ну или наоборот:

Таким образом, закон распределения вероятностей зависимой системы :

Контроль: , что и требовалось проверить. …Возможно, у вас возник вопрос, а почему я рассматриваю именно 8, а не 36 карт? Да просто для того, чтобы дроби получились не такими громоздкими.

Теперь немного проанализируем результаты. Если просуммировать вероятности по строкам: , то получится в точности закон распределения случайной величины :

Легко понять, что это распределение соответствует ситуации, когда «иксовый» игрок тянет карту один, без «игрекового» товарища, и его математическое ожидание:
– равно вероятности извлечения червы из нашей колоды.

Аналогично, если просуммировать вероятности по столбцам, то получим закон распределения одиночной игры второго игрока:

с тем же матожиданием

В силу «симметрии» правил игры, распределения получились одинаковыми, но, в общем случае, они, конечно, различны.

Помимо этого, полезно рассмотреть условные законы распределения вероятностей. Это ситуация, когда одна из случайных величин уже приняла какое-то конкретное значение, или же мы предполагаем это гипотетически.

Пусть «игрековый» игрок тянет карту первым и извлекает не черву . Вероятность этого события составляет (суммируем вероятности по первому столбцу таблицы – см. вверху). Тогда, из той же теоремы умножения вероятностей зависимых событий получаем следующие условные вероятности:
– вероятность того, что «иксовый» игрок вытянет не черву при условии, что «игрековый» вытянул не черву;
– вероятность того, что «иксовый» игрок вытянет черву, при условии, что «игрековый» вытянул не черву.

…Все помнят, как избавляться от четырёхэтажных дробей? И да, формальное, но очень удобное техническое правило вычисления этих вероятностей: сначала следует просуммировать все вероятности по столбцу, и затем каждую вероятность разделить на полученную сумму.

Таким образом, при условный закон распределения случайной величины запишется так:

, ОК. Вычислим условное математическое ожидание:

Теперь составим закон распределения случайной величины при условии, что случайная величина приняла значение , т. е. «игрековый» игрок извлёк карту червовой масти. Для этого суммируем вероятности 2-го столбца таблицы (см. вверху): и вычисляем условные вероятности:
– того, что «иксовый» игрок вытянет не черву,
– и черву.
Таким образом, искомый условный закон распределения:

Контроль: , и условное математическое ожидание:
– разумеется, оно получилось меньше, чем в предыдущем случае, так как «игрековый» игрок убавил количество черв в колоде.

«Зеркальным» способом (работая со строками таблицы ) можно составить – закон распределения случайной величины , при условии, что случайная величина приняла значение , и условное распределение , когда «иксовый» игрок извлёк черву. Легко понять, что в силу «симметрии» игры, получатся те же распределения и те же значения .

Для непрерывных случайных величин вводятся такие же понятия условных распределений и матожиданий, но если в них нет горячей надобности, то лучше продолжить изучение этого урока.

На практике в большинстве случаев вам предложат готовый закон распределения системы случайных величин:

Пример 4

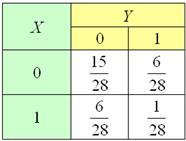
Двумерная случайная величина задана своим законом распределения вероятностей:

…Хотел рассмотреть таблицу побольше, но решил-таки не маньячить, ведь главное разобраться в самом принципе решения.

Требуется:

1) Составить законы распределения и вычислить соответствующие математические ожидания. Сделать обоснованный вывод о зависимости или независимости случайных величин .

Это задание для самостоятельного решения! Напоминаю, что в случае независимости СВ законы должны получиться одинаковыми и совпасть с законом распределения случайной величины , и законы – совпасть с . Десятичные дроби, кто не знает или позабыл, удобно делить так: .
Свериться с образцом можно внизу страницы.

2) Вычислить коэффициент ковариации.

Сначала разберёмся в самом термине, и откуда он вообще произошёл: когда случайная величина принимает различные значения, то говорят, что она варьируется, и количественное измерение этой вариации, как вы знаете, выражается дисперсией. Используя формулу вычисления дисперсии, а также свойства матожидания и дисперсии, нетрудно установить, что:

то есть при сложении двух случайных величин суммируются их дисперсии и добавляется дополнительное слагаемое, характеризующее совместную вариацию или коротко – ковариацию случайных величин.

Ковариация или корреляционный момент – это мера совместной вариации случайных величин.

Обозначение: или

Ковариация дискретных случайных величин определяется, сейчас буду «выражаться»:), как математическое ожидание произведения линейных отклонений этих случайных величин от соответствующих матожиданий:

Если , то случайные величины зависимы. Образно говоря, ненулевое значение говорит нам о закономерных «откликах» одной СВ на изменение другой СВ.

Ковариацию можно вычислить двумя способами, я рассмотрю оба.

Способ первый. По определению математического ожидания:

«Страшная» формула и совсем не страшные вычисления. Сначала составим законы распределения случайных величин и – для этого суммируем вероятности по строкам («иксовая» величина) и по столбцам («игрековая» величина):

Взгляните на исходную верхнюю таблицу – всем понятно, как получились распределения? Вычислим матожидания:
и отклонения значений случайных величин от соответствующих математических ожиданий:

Полученные отклонения удобно поместить в двумерную таблицу, внутрь которой затем переписать вероятности из исходной таблицы:

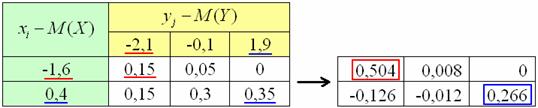
Теперь нужно вычислить все возможные произведения , в качестве примера я выделил: (красный цвет) и (синий цвет). Вычисления удобно проводить в Экселе, а на чистовике расписать всё подробно. Я привык работать «по строкам» слева направо и поэтому сначала перечислю все возможные произведения с «иксовым» отклонением -1,6, затем – с отклонением 0,4:

Способ второй, более простой и распространённый. По формуле:

Матожидание произведения СВ определяется как и технически всё очень просто: берём исходную таблицу задачи и находим все возможные произведения на соответствующие вероятности ; на рисунке ниже я выделил красным цветом произведение и синим произведение :

Сначала перечислю все произведения со значением , затем – со значением , но вы, разумеется, можете использовать и другой порядок перебора – кому как удобнее:

Значения уже вычислены (см. 1-й способ), и осталось применить формулу:

Как отмечалось выше, ненулевое значение ковариации говорит нам о зависимости случайных величин, причём, чем оно больше по модулю, тем эта зависимость ближе к функциональной линейной зависимости . Ибо определяется через линейные отклонения.

Таким образом, определение можно сформулировать точнее:

Ковариация – это мера линейной зависимости случайных величин.

С нулевым значением всё занятнее. Если установлено, что , то случайные величины могут оказаться как независимыми, так и зависимыми (т. к. зависимость может носить не только линейный характер). Таким образом, этот факт в общем случае нельзя использовать для обоснования независимости СВ!

Однако, если известно, что независимы, то . В этом легко убедиться аналитически: так как для независимых случайных величин справедливо свойство (см. предыдущий урок), то по формуле вычисления ковариации:

Какие значения может принимать этот коэффициент? Коэффициент ковариации принимает значения, не превосходящие по модулю – и чем больше , тем сильнее выражена линейная зависимость. И всё вроде бы хорошо, но есть существенное неудобство такой меры:

Предположим, мы исследуем двумерную непрерывную случайную величину (готовимся морально :)), компоненты которой измеряются в сантиметрах, и получили значение . Кстати, какая размерность у ковариации? Коль скоро – сантиметры, и – тоже сантиметры, то их произведение и матожидание этого произведения – выражается в квадратных сантиметрах, т. е. ковариация, как и дисперсия – есть квадратичная величина.

Теперь предположим, что кто-то изучил ту же систему , но использовал не сантиметры, а миллиметры. Так как 1 см = 10 мм, то ковариация увеличится в 100 раз и будет равна !

Поэтому удобно рассмотреть нормированный коэффициент ковариации, который давал бы нам одинаковое и безразмерное значение. Такой коэффициент получил название, продолжаем нашу задачу:

3) Коэффициент корреляции. Или, точнее, коэффициент линейной корреляции:

, где – стандартные отклонения случайных величин.

Коэффициент корреляции безразмерен и принимает значения из промежутка:

(если у вас на практике получилось другое – ищите ошибку).

Чем больше по модулю к единице, тем теснее линейная взаимосвязь между величинами , и чем ближе к нулю – тем такая зависимость выражена меньше. Взаимосвязь считается существенной, начиная примерно с . Крайним значениям соответствует строгая функциональная зависимость , но на практике, конечно, «идеальных» случаев не встретить.

Очень хочется привести много интересных примеров, но корреляция более актуальна в курсе математической статистики, и поэтому я приберегу их на будущее. Ну а сейчас найдём коэффициент корреляции в нашей задаче. Так. Законы распределения уже известны, скопирую сверху:

Матожидания найдены: , и осталось вычислить стандартные отклонения. Табличкой уж оформлять не буду, быстрее подсчитать строкой:

Ковариация найдена в предыдущем пункте , и осталось рассчитать коэффициент корреляции:
, таким образом, между величинами имеет место линейная зависимость средней тесноты.

Четвёртое задание опять же более характерно для задач математической статистики, но на всякий случай рассмотрим его и здесь:

4) Составить уравнение линейной регрессии на .

Уравнение линейной регрессии – это функция , которая наилучшим образом приближает значения случайной величины . Для наилучшего приближения, как правило, используют метод наименьших квадратов, и тогда коэффициенты регрессии можно вычислить по формулам:
, вот это чудеса, и 2-й коэффициент:

Таким образом, искомое уравнение регрессии:

ну и давайте ради исследовательского интереса я скопирую табличку сверху:

и вычислю значения функции:
– в результате получился результат, который близок к наиболее вероятному (см. 2-ю снизу строку) значению ;
– тоже неплохо, это приближение попало между наиболее вероятными (см. нижнюю строку) значениями

Вполне и вполне приличные результаты, несмотря на невысокий коэффициент корреляции. И, наверное, вы уже догадались, что чем ближе по модулю к единице, тем точнее функция приближает наиболее вероятные значения случайной величины . Но уравнение линейной регрессии, конечно, больше применимо к двумерной непрерывной случайной величине, поскольку позволяет осуществлять реальное прогнозирование, например, наиболее вероятного веса человека по заданному росту.

Творческое задание для самостоятельного решения:

Пример 5

Вычислить коэффициенты ковариации и корреляции для демонстрационного примера данного урока (с картами червовой масти) и оценить тесноту линейной связи между СВ.

после чего с нетерпением переходим к системам непрерывных случайных величин.

Решения и ответы:

Пример 4, пункт 1. Решение:

1) Составим закон распределения , для этого суммируем все вероятности соответствующего столбца: и делим каждую вероятность на полученную сумму:

Так как вероятности изменились, то мы имеем дело с условными вероятностями, и из этого можно сразу сделать вывод, что случайные величины зависимы.

! Примечание: в случае независимости СВ вероятности остались бы прежними! – желающие могут проверить данный факт на любом примере предыдущего урока.

Таким образом, условное распределение вероятностей:

и условное математическое ожидание:

2) Составим закон распределения . Суммируем вероятности соответствующего столбца: и делим каждую из них на полученную сумму:

Таким образом:

И здесь делаем вывод, что распределение случайной величины зависит от того, какое значение приняла случайная величина , что является ещё более убедительным обоснованием зависимости этих СВ.
Условное матожидание: .

3) Аналогично находим закон распределения :

Таким образом, при случайная величина достоверно примет значение

и, очевидно, .

4) Чтобы составить закон распределения , нужно просуммировать все вероятности соответствующей строки: и разделить каждую из них на полученную сумму:

5) И, наконец,

Контроль: , ч.т.п.

Пример 5. Решение: коэффициент ковариации вычислим по формуле:

уже найдены,

Таким образом:

Коэффициент корреляции вычислим по формуле:

Найдём стандартные отклонения случайных величин:

Закон распределения точно такой же, поэтому .

Таким образом:

Полученное значение достаточно близко к нулю, что говорит о слабой зависимости случайных величин. Тем не менее, знак «минус» показывает, что при увеличении значения одной из случайных величин (от 0 до 1) уменьшаются шансы извлечения червы другим игроком

Примечание: при достаточно малых значениях (ниже 0,3-0,4 по модулю) построение уравнения линейной регрессии теряет смысл, т.к. оно недостоверно приблизит исходные данные.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Зависимые и независимые случайные величины.Условные законы распределения и ковариация дискретных СВ

Зависимые и независимые случайные величины.
Условные законы распределения и ковариация дискретных СВ