Сумма степенного ряда

Данный урок лучше всего изучать по «горячим следам» сразу же после статьи о разложении функции в степенные ряды, поскольку сейчас мы будем решать обратную задачу. Пожалуйста, откройте таблицу разложений функций в степенные ряды и по возможности отправьте файл на печать – чтобы справочный материал был постоянно перед глазами. На бумаге, на столе и перед глазами. Это важно!

Суть задания предельно простА: дан степенной ряд. Например:

И по условию требуется найти сумму этого ряда, то есть, функцию, к которой он сходится. …Не понятно, что значит «ряд сходится к функции»? Срочно читаем предыдущую статью!

Как найти сумму степенного ряда? Здесь не существует какого-то жёсткого алгоритма решения, но есть общие ориентиры, с которыми мы сегодня и познакомимся.

В первую очередь целесообразно обратиться к таблице и попытаться выяснить – НА КАКОЕ РАЗЛОЖЕНИЕ больше всего похож предложенный ряд? У нашего ряда в знаменателях по порядку идут факториалы, и поэтому он больше всего напоминает разложение экспоненты: . Однако тут степени «альф» совпадают с номерами факториалов, а у нас степень «икса» «отстаёт» на единицу. Что делать? Поправим ситуацию умножением и делением ряда на «икс»:

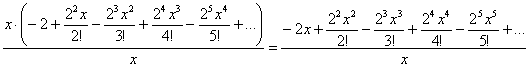
Теперь обращаем внимание, что наверху не хватает слагаемого-«единички». Да какие проблемы? – прибавим её да вычтем:

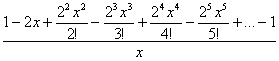
Что смущает ещё? Знакочередование. Его в разложении экспоненты нет. Но в данном случае «минусы» можно «затолкать» под нечётные степени, а под чётными степенями их «возродить»:

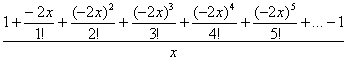
Таким образом, мы сконструировали разложение экспоненты для :

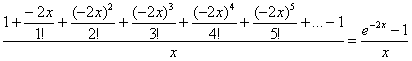
Итак:

Другим немаловажным вопросом является область сходимости ряда. Иными словами, ПРИ КАКИХ значениях «икс» наш ряд будет сходиться к функции ? В таблице указано, что экспоненциальный ряд сходится при любом «альфа», но у нас есть одна загвоздочка: найденная функция не определена в точке . Однако ряд в этой точке сходится! И действительно – если подставить ноль, то получается конечное число:

Таким образом, сумма ряда запишется кусочным образом:

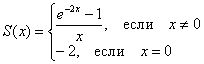
Как и сумма числового ряда, она стандартно обозначается буквой «эс».

Причём, интересно отметить, что данная сумма непрерывна. И в самом деле – используя соответствующий замечательный предел, получаем:

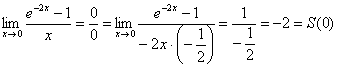
Однако в точке ряд сходится всё же НЕ к функции (и похожие примеры, кстати, уже встретились в статье о разложении функции в ряд).

Несмотря на то, что интервалы сходимости типовых рядов я указал в таблице, важно понимать, откуда они взялись. Как, например, определить область сходимости только что разобранного ряда безо всякой таблицы? Записываем его в свёрнутом виде, подобрав общий член:

и, пользуясь обычным алгоритмом, выясняем, что ряд сходится на всей числовой прямой.

С помощью найденной суммы легко рассчитать сумму любого числового ряда из этого «семейства». Так, например, при получаем ряд , сумма которого равна: – на всякий случай напомню, что это сумма всех его членов:

Если , то получим ряд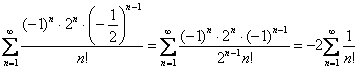
с суммой 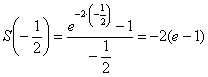, откуда, кстати, открывается волнующая тайна:
.

И так далее – можно рассмотреть любое значение «икс» из области сходимости ряда.

В статье о сумме числовых рядов мы потихонечку долбили их ломом (да и то немногие поддавались), и сейчас в наших руках оказался целый отбойный молоток! Пользуйтесь и наслаждайтесь!

Другой пример: – найдём сумму данного степенного ряда.

Именно в свёрнутом виде он чаще всего и предлагается, и само собой ряд удобно расписать:

Анализируя таблицу, приходим к выводу, что наш «пациент» больше всего напоминает разложение , причём «альфа», очевидно, равно «иксу» в кубе. Выносим за скобки «минус» и «лишний» и показываем, что :

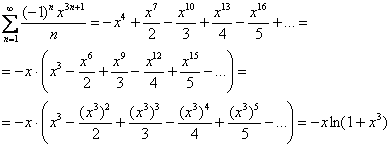
Определим, на каком промежутке ряд сходится к функции . Интервал сходимости ряда можно найти опять же стандартным способом, либо воспользоваться табличным «подарком»:

Сходимость ряда на концах интервала выясняем как обычно – прямой подстановкой:

если , то – расходится;
если , то – сходится условно.

Таким образом, ряд сходится лишь на полуинтервале . Вне этого промежутка он расходится и его суммы, понятное дело, не существует.

Итак: , если – в отличие от предыдущего примера, выбор «иксов» тут небогат.

И здесь ещё хочется заострить внимание на разнице в понятиях и обозначениях:

через обозначается функция (сама по себе),
а через – конкретно сумма ряда (на том или ином промежутке).

Разминочные задания для самостоятельного решения:

Найти сумму следующих степенных рядов:

а)
…ну а кому сейчас легко? =)

б)
Дополнительно: записать числовой ряд для и вычислить его сумму.

Краткие решения и ответы в конце урока.

Наверное, все понимают, как выполнять проверку таких заданий – для этого нужно разложить полученную функцию обратно в ряд. Но это уже пройденное, да и к тому же простое действие, и поэтому я его расписывать не буду.

Алгебраические преобразования рядов могут быть весьма замысловаты, однако дело не ограничиваются только ими. Как многие подозревали, производные с интегралами поджидают нас и здесь! Ну а куда ж без них? =) Пожалуйста, освежите воспоминания с помощью таблицы производных и таблицы интегралов (откроются на соседних вкладках) – их тоже по возможности распечатайте и положите перед глазами. …Есть? Поехали:

Почленное дифференцирование и интегрирование степенного ряда

Пусть степенной ряд сходится к своей сумме на некотором промежутке. …Теоремы формулировать не буду – проще рассказать своими словами:

Степенной ряд можно почленно дифференцировать в любой точке внутри его промежутка сходимости: 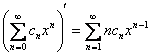, при этом интервал сходимости полученного ряда останется точно таким же, а его сумма на данном интервале будет равна: .

И на всякий случай поясню, что значит «почленно» – если расписать ряд подробно, то согласно свойству линейности, он дифференцируется по каждому члену отдельно:

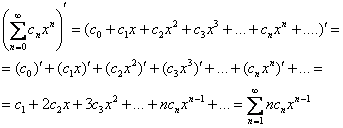
Степенной ряд можно почленно интегрировать внутри его промежутка сходимости, но здесь ситуация занятнее. Если мы будем его интегрировать по фиксированному отрезку , то получим числовой ряд:

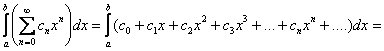
всё чинно-почленно:

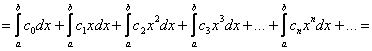
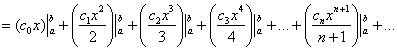– и в самом деле, членами же этого ряда являются числа (вспоминаем формулу Ньютона-Лейбница).

Геометрический смысл и практическое применение такого интегрирования мы разберём на уроке о приближённом вычислении интеграла, ну а сейчас нас ждут другие подвиги. А именно, почленное интегрирование по отрезку с переменным верхним пределом , где «икс» может принимать произвольное значение из интервала сходимости, при этом в качестве нижнего предела удобно выбрать ноль. По той же самой формуле Ньютона-Лейбница, получается уже не числовой, а функциональный ряд – распишу подробно:

формально здесь можно сказать, что вместо «икс» мы подставляем «икс»:

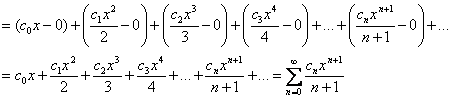
Причём: полученный ряд обладает тем же интервалом сходимости, что и исходный ряд, а его сумму можно найти по формул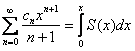е , где , напоминаю – сумма ряда

Важнейшим условием осуществления этих действий является равномерная сходимость степенных рядов – анонсирую и рекомендую прочитать эту интереснейшую статью! Но прежде освоим технику. Начнём с тех же табличных разложений, некоторые из которых как раз получены с помощью дифференцирования и интегрирования.

Выведем, например, разложение арктангенса. Для этого разложим его производную в стандартный ряд :

после чего проинтегрируем этот ряд в его интервале сходимости :

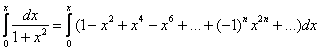
далее для краткости записи я буду дифференцировать/интегрировать ряды «один махом»:

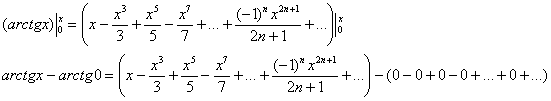
В результате:

Поскольку «родительский» биномиальный ряд сходится на интервале , то и полученный ряд тоже будет сходиться на этом интервале. А может быть ещё и на его концах. Проверяем:

Оба числовых ряда сходятся условно, таким образом, ряд сходится к арктангенсу в области (вспоминаем картинку из предыдущей статьи).

По этой же схеме выводятся разложения логарифма и арксинуса – потренируйтесь самостоятельно.

С помощью «новых» действий можно найти разложения некоторых других функций.

Классический Пример 1

Разложить в ряд функцию и указать его интервал сходимости.

Решение: по «общим очертаниям» предложенная функция сильно напоминает производную от . И действительно:

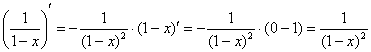
Таким образом, искомый ряд получается фактически на «автомате» – дифференцированием стандартного разложения на его интервале сходимости:

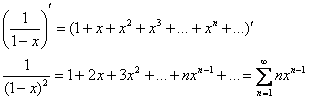
Так как исходный ряд сходится при , то полученный ряд тоже будет сходиться на данном интервале. Осталось узнать, что происходит на концах:
– расходится;
– расходится.

Ответ: , ряд сходится при

Выполним проверку:

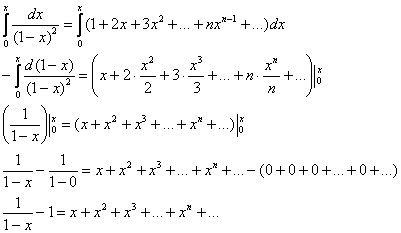
и перебрасываем единичку направо:
– в результате получено исходное разложение, что и требовалось проверить.

Таким образом, всегда держите на заметке, что предложенная функция может быть производной либо интегралом от чего-нибудь табличного. Однако сегодняшний урок посвящён обратной задаче, и применительно к разобранной «классике» она формулируется так:

Пример 1*

Найти сумму ряда

А вот это уже труднее – ведь мы «ещё не знаем», что данный ряд получен дифференцированием ряда , и данный факт можно запросто не увидеть. Впрочем, тут существует чёткий критерий, позволяющий «прозреть»:

Решение: анализируя ряд , приходим к выводу, что он мало похож на что-то стандартное, но зато в таблице есть его «ближайший родственник» , к которому мы и обратимся за помощью.

Для этого нужно «избавиться» от множителя . Каким образом? Разделить его на самого себя! И такую возможность нам предоставляет интегрирование – здесь я оформлю действия в свёрнутой форме:

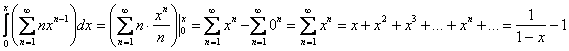
Теперь нужно «вернуть должок» дифференцированием:

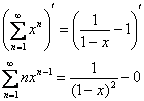
Ответ: на интервале

Таким образом, «почленёнка» помогает нам «убрать с дороги» неудобные множители, и это действительно очень мощный инструмент:

Пример 2

Найти сумму степенного ряда

Но перед тем как решать, важная преамбула: несмотря на то, в условии этого не прописано – нам всё равно потребуется найти область сходимости ряда. Причина, думаю, понятна – ведь сумма в общем случае существует далеко не везде, и если в ответе указать только её, то это будет серьёзнейшим недочётом.

Наверное, многие уже «набили руку» на числовых рядах и способны найти область сходимости устно. В частности, здесь хорошо видно, что предложенный ряд сходится на промежутке . Как выполнить экспресс-анализ? Берём какую-нибудь правильную дробь, например, и выполняем подстановку:
– данный ряд сходится по признаку Даламбера. И, очевидно, что после подстановки любой дроби из интервала будут получаться похожие ряды.

Далее тестируем произвольное «внешнее» значение, например :
– расходится по тому же признаку Даламбера. Кстати, здесь вообще не выполнен необходимый признак сходимости, т. к. более высокого порядка роста, чем .

Проверка концов интервала тоже осуществляется в считанные секунды:

Таким образом, к решению задачи нужно подойти во «всеоружии» – с известной областью сходимости и записать следующую фразу: данный ряд сходится на . Как вариант, можно привести развёрнутые выкладки нахождения области – но это если вам трудно или если не лень.

Ну а теперь амбула (с). Во-первых, не будем торопиться с «тяжёлой артиллерией» – вдруг она не потребуется? Сначала распишем ряд подробно:
и вновь обратим свой взор на таблицу…. – наш ряд напоминает разложение арктангенса, однако ж, там знакочередование, и никакими алгебраическими «ухищрениями» эти ряды не «состыковать». Другие табличные разложения подходят к нашему случаю ещё меньше.

Что делать? Глядя на степени «икса» и числа внизу, в голову приходит светлая мысль избавиться от последних. Дифференцируем ряд на его интервале сходимости :

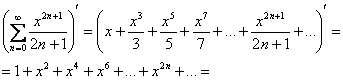
и всё дело свелось к простому табличному разложению:

Но коль скоро мы дифференцировали, то за это придётся «заплатить» интегрированием:

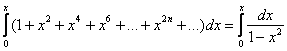
Справа в качестве суммы исходного ряда «нарисовался» «высокий» логарифм:

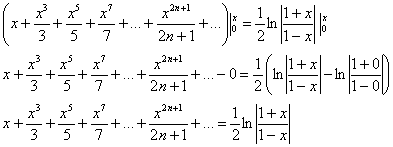
Ответ: на интервале

Обратите внимание, что в решении фигурировал ряд с суммой на том же интервале, но об этом нас никто не спрашивал.

Сегодня я буду разбирать простые примеры, а вам предлагать интересные:))

Пример 3

Найти сумму ряда

Краткое решение и ответ в конце урока.

Но это ещё далеко не все секреты:

Пример 4

Найти сумму ряда

Решение: данный ряд сходится в области (проанализируйте, почему).

Как обычно расписываем ряд, чтобы поискать «лёгкий путь»:
И после изучения таблицы и некоторых «трепыханий» мы приходим к грустному выводу, что ничего путного не получается. Очевидное дифференцирование тоже выглядит не особо перспективным:

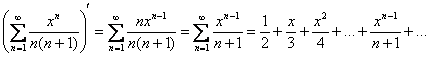
Но вот как бы было хорошо «избавиться» в знаменателе не от , а от . И возникает вопрос, а нельзя ли организовать такую возможность? Можно! Чтобы наверху получить ряд следует искусственно умножить и разделить на «икс». Однако этим действием мы «выключаем из игры» точку , которая входит в область сходимости. И поэтому в ней необходимо вычислить сумму ряда: , чтобы жить спокойно:

Прерываем решение «звёздочкой» и работаем с новым «кадром»:

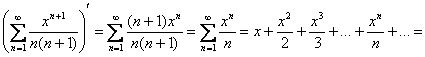
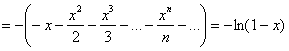– здесь всё свелось к разложению для .

Выполняем обратное действие:

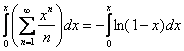
Интеграл правой части, надо сказать, неприятный, и поэтому с ним лучше разобраться отдельно, причём без пределов интегрирования:

Интегрируем по частям:

и знакомый приём с дробями,… не запутаться бы тут в знаках:

Контроль:
, ч. т. п.

Таким образом:

И теперь главное не забыть про «звёздочку»:

Но это ещё не всё! Как подсказывает математическое чутьё, тонким местом исследования являются концы интервала сходимости – и действительно, полученная функция имеет проблемы не только с нулём, но ещё и на правом конце области сходимости ряда. Придётся исследовать его отдельно:
– и к нашей радости сумма числового ряда отыскивается по стандартной схеме. Метод неопределённых коэффициентов работает в своей простейшёй ипостаси:

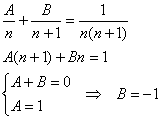
Таким образом:

Запишем частичную сумму ряда:

Сумма исследуемого числового ряда:

И, наконец, сумма ряда функционального:

Ответ: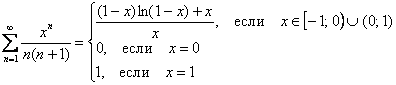

Такой вот простенький ряд =)

Следует отметить, что искусственный приём с домножением и делением на самом деле можно использовать и после «очевидного» дифференцирования, но там получатся более сложные вычисления.

Вам понравилось? Но и это ещё не всё! В свете последней части задания всплывает… какой же я тонкий лирик:))

второй способ решения: разложим числовую часть общего члена степенного ряда в сумму дробей (см. выше) и представим его в виде суммы двух рядов:

строго говоря, здесь нужны кой-какие комментарии, но я их опущу.

Дальнейшие действия очевидны – веник ломаем по прутикам:

1)
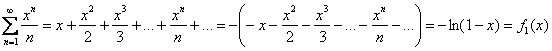
(берём на заметку значение )

2)
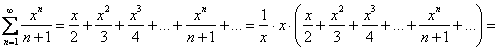
(берём на заметку значение )

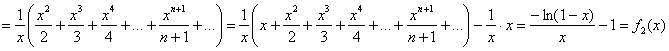
Таким образом, функция, к которой сходится ряд на промежутках :

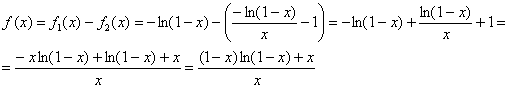
Точки исследуются отдельно, и что приятно, для последней уже есть готовенький числовой ряд .

Ответ: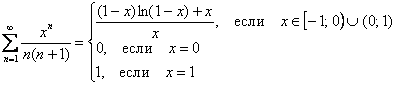

На всякого мудреца довольно простоты! И никакого дифференцирования с интегрированием =)

Кстати, не нужно думать, что этот способ является каким-то экзотическим – он используется во многих тематических заданиях, причём иной ряд можно разделить даже на 3 части.

Обещанная интересность для самостоятельного решения:

Пример 5

Найти сумму ряда

Примерный образец чистового оформления задачи в конце урока.

Кроме того, встречаются задачи, в которых приходится дифференцировать 2 раза подряд, что «карается» последующим двукратным интегрированием. При этом справедливо следующее…, а чего скромничать – изучим ситуацию в общем виде:

пусть функция разложима в степенной ряд на некотором интервале:

ну, или можно сказать, что сумма степенного ряда равна – смотря с какой стороны рассуждать.

Как уже отмечалось, при почленном дифференцировании ряда на данном интервале получившийся ряд сойдётся к производной:

При повторном дифференцировании на том же интервале суммой нового ряда будет вторая производная:

И более того, если у функции существуют все производные высших порядков, то дифференцировать можно до бесконечности:

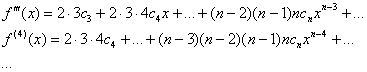
Причём, соответствующие ряды, не нужно быть пророком, сходятся к своим производным, а интервал сходимости не меняется.

И, разумеется, справедливы обратные выкладки с интегрированием. Но вместо них небольшой фокус – вычислим значения функции и всех её производных в точке :

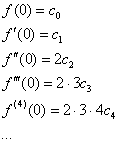
Далее выразим коэффициенты , …очевидно, что – после чего подставим их в разложение :

;-)

В большинстве задач этого урока мы сначала дифференцировали, а затем интегрировали, но само собой допустим и обратный порядок. Так, в Примере 1* всё было наоборот – и уже из этого простого ряда яснА основная задача первоочередного интегрирования – расчистить «верхний этаж»:

Пример 6

Найти сумму степенного ряда

Решение: данный ряд сходится на интервале .

И вновь не будем пренебрегать поиском простых путей:
, …которых, увы, не видно.

Очевидно, что основной нашей помехой является множитель , который надо «убрать». Попробуем проинтегрировать ряд почленно:

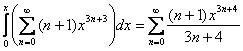
Не айс,… вот если бы внизу нарисовалось – тогда да. Но это ж можно организовать – нужно только понизить изначальную степень на единицу. А делается это очень просто – «отщипываем» один «икс» и выносим его за пределы ряда:

Далее работаем с «модифицированным» рядом:

Приводим ситуацию в равновесие дифференцированием:

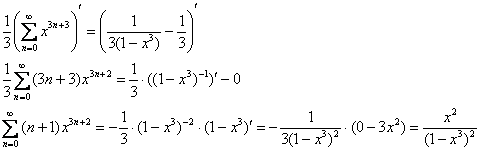
И не забываем, что это ещё не окончательная сумма:

Ответ: на интервале

Заметьте, что здесь нет проблем со знаменателем, так как значение не входит в область сходимости ряда – не забываем контролировать такие моменты!

И в заключение…, нет, пожалуй, успокоительная задача:)

Пример 7

Найти сумму степенного ряда

Моя версия решения внизу страницы.

Наверное, у всех уже в глазах мельтешит от разложений, и поэтому самое время принять лекарство – равномерную сходимость ряда, которая по иронии судьбы и стала тому первопричиной :) Кроме того, на грядущем уроке вы узнаете, как определяется сумма произвольного функционального ряда.

Пожалуйста, сообщите, если где заметили опечатку или ошибку, потому что статья была действительно одна из самых кропотливых, и вы имели счастье, кстати, познакомиться с её 6-й версией. Всё время казалось «всё», но каждый раз всплывали… к концу статьи я превратился в толстого циника)… ещё какие-то интересные факты, примеры и нюансы. Что-то добавлялось, редактировалось, что-то «выбрасывалось». И на самом деле ещё есть о чём рассказать! Поэтому нужно пересилить себя и поставить

Решения и ответы:

Разминочное задание. Решение:

а) Распишем несколько членов ряда, раскроем скобки и перегруппируем слагаемые:

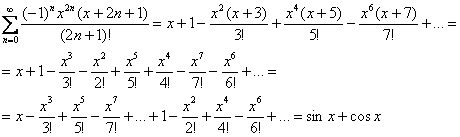
Оба разложения сходятся на всей числовой прямой.

Ответ: на интервале

б) Ориентируемся на табличное разложение :

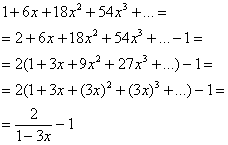
Найдём область сходимости ряда. Согласно таблице, ряд сходится при . В данном случае :
– разделим все части на три:

Исследуем сходимость ряда на концах найденного интервала. Для этого запишем его в свёрнутом виде и подставим граничные значения:

Оба числовых ряда расходятся, т. к. не выполнен необходимый признак сходимости.

Ответ: ряд сходится на интервале , сумма ряда: .
Если , то получаем числовой ряд , сумма которого равна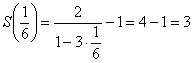
Примечание: также здесь можно использовать формулу суммы бесконечно убывающей геометрической прогрессии:

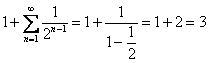
Пример 3. Решение: дифференцируем ряд в его интервале сходимости (на всей числовой прямой) и находим сумму полученного ряда:

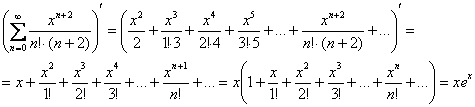
Интегрируем:

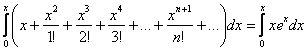
Интеграл правой части берётся по частям:

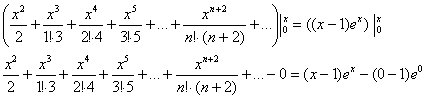
Ответ: на интервале

Пример 5. Решение: данный ряд сходится в области . Ориентируясь на разложение , выполним следующие преобразования:

Вычислим сумму ряда в точке

Ответ: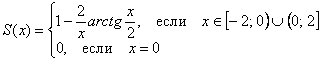

Способ второй: данный ряд сходится в области . Вычислим его сумму в середине и выполним следующее преобразование:

Дифференцируем полученный ряд:

Примечание: использовали разложение для .
Интегрируем:

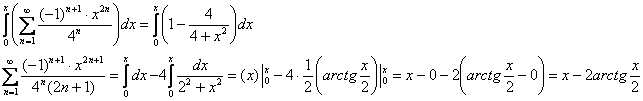
Таким образом:

Ответ: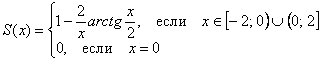

Пример 7. Решение: данный ряд сходится на интервале .
Разделим его на 2 части:

1) Найдём сумму
Поскольку «икс» оказался в знаменателе, то контролируем точку , в которой сумма ряда: .
Интегрируем ряд почленно:

Дифференцируем:

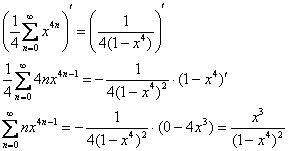
Таким образом: