Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Как найти частные производные неявно заданной функции?

Почти так же, как и производную неявной функции одной переменной. С поправкой на особенности дифференцирования ФНП, которые мы подробно разобрали на уроках Частные производные функции двух и трёх переменных. …На данной странице, думается, задержались калачи тёртые, и поэтому, перефразируя известного киногероя, я буду грузить вас аккуратно, но сильно =)

Начнём с функции двух переменных , неявный вид которой чаще всего обозначают уравнением. Обе формы уже неоднократно встречались в предыдущих статьях раздела, но, тем не менее, элементарный пример:

 – функция плоскости в явном виде;
 – та же функция, заданная неявно.

Последняя запись, как вы прекрасно знаете – есть не что иное, как общее уравнение плоскости, из которого легко получить функциональный вид. Однако сегодня нас мало интересует, можно ли выразить «зет» или нельзя, поскольку принципиальный алгоритм дифференцирования неявно заданной функции совершенно от этого не зависит. Давайте вспомним общую схему решения:

Пример 1

Найти частные производные 1-го порядка функции

Решение: Найдём . Сначала на обе части уравнения «навешиваем» штрихи с «иксовым» подстрочным индексом:

Далее пользуемся тривиальным правилом :


 – это, очевидно, и есть наша частная производная , таким образом:

И на завершающем шаге выражаем результат:

Аналогично с частной производной по «игрек»:

Ответ:

Естественно, что производные получились точно такими же, что и при дифференцировании «обычной» функции:

Но то была, конечно же, шутка:

Пример 2

Дана функция . Найти частные производные 1-го и 2-го порядков.

Слишком просто? Я бы не спешил с выводами ;-)

Решение: сначала найдём частные производные 1-го порядка. По «икс»:

В правой части находится «живой» множитель «икс», а значит, необходимо применить правило дифференцирования произведения :

Поскольку буква «зет» САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (), то при нахождении   следует использовать правило дифференцирования сложной функции . Тоже знакомый вам мотив! В данном случае внешняя функция – это степень, а внутренняя функция – это собственно функция «зет»:

Причешем результат:

Теперь в левой части нужно собрать слагаемые, которые содержат производную, а справа – всё остальное:

Выносим  за скобки и сбрасываем множитель в правую часть:

Готово.

Найдём частную производную по «игрек»:

Так как «икс» считается константой, то в правой части сразу выносим его за знак производной:

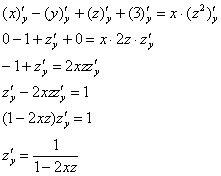
Готово.

Как и для функции одной переменной, существует второй способ решения, его слёзно попросили разобрать те, кого я замучил первым способом :) Берём исходное уравнение , переносим все слагаемые в одну часть:  и рассматриваем функцию трёх переменных . Тогда частные производные можно найти по следующим формулам:

И мучения превращаются в удовольствие:

Таким образом:

Найдём частные производные 2-го порядка. Как я уже рекомендовал, сначала выгоднее найти смешанные частные производные и убедиться, что , проверив тем самым правильность предыдущих действий.

Как найти производную ? Существует прямой путь  с применением правила , но в данном случае он не очень удобен. Для дифференцирования по «игрек» лучше выбрать не финальную частную производную , а предшествующее равенство  и «навесить» на обе его части «игрековые» штрихи:
 
Этот трюк, кстати, не нов – о нём я рассказывал на уроке Производные высших порядков.

Слева используем правило  и не забываем, что «икс» считается константой:

Слагаемое с нужной нам производной  оставляем слева:

Производные высших порядков по возможности принято выражать только через «икс», «игрек» и «зет». А такая возможность здесь более чем реалистична – подставим найденные ранее  в правую часть и упростим результат:

И по завершению генеральной уборки сбрасываем множитель :

Найдём «родственницу» . Опять – для дифференцирования по «икс» можно взять не саму производную , а предшествующее равенство , но ради разнообразия я пойду прямой дорогой:

Подставим  и избавимся от трёхэтажности дроби:

Таким образом, , что мы и хотели увидеть.

На завершающем этапе предельно внимательно разбираемся с производными .

Вторую производную по «икс» рациональнее найти не прямым дифференцированием первой производной  (получится громоздкая дробь), а из равенства . Навешиваем «иксовые» штрихи на обе части:

Слева дважды применяем правило , главное, тут не запутаться:

Подставляем в правую часть :

Окончательно:

Следует отметить, что здесь существует очень хорошая возможность проверить результат. Для этого вторую производную нужно взять напрямую:  и таки разобраться с громоздкой дробью.

Тяжеловато? Ну я же обещал =)

Впрочем, оставшаяся производная простецкая, используем дифференцирование «в лоб»:

Подставим :

Проверка тут зеркальна – дифференцируем по «игрек» обе части равенства

И самый приятный момент:

Ответ:

Как найти частные производные более высоких порядков? По тем же принципам. Так, например, производная  отыскивается как прямым дифференцированием , так и навешиванием «игрековых» штрихов на левую и правую часть равенства .

Какой из этих двух способов удобнее – нужно смотреть по ситуации.

Аналогичное задание для самостоятельного решения:

Пример 3

Найти частные производные 1-го и 2-го порядков неявно заданной функции.

К слову, из этой солянки элементарно выражается «зет», но сейчас весь интерес состоит в том, чтобы провести решение «неявным образом». Примерный образец чистового оформления задачи в конце урока.

Техника нахождения частных производных от неявно заданной функции разобрана до мелочей, но остался ещё один небольшой вопрос: как в подобных случаях находить частные производные в какой-либо конкретной точке? Рассмотрим пару задач на эту тему:

Пример 4

Вычислить значения частных производных функции  в точке .

Решение: на всякий случай удостоверимся, что точка  действительно принадлежит поверхности . Для этого подставим координаты  в левую часть:
, что и требовалось проверить.

Найдём частную производную по «икс»:

Поскольку «игрек» считается константой, то  – тоже константа. Но особое внимание обратите на  – тут двойное вложение: под степень вложен косинус, а под косинус – функция «зет»:

Для удобства уберём минусы (умножим обе части на –1) и воспользуемся известной тригонометрической формулой :

Производную в точке  можно вычислить уже сейчас – для этого следует подставить её координаты  в левую часть и выразить :

Но в данном случае более прост «цивилизованный» путь, сначала выражаем производную:

Затем находим производную в точке:

Аналогично разбираемся с частной производной по «игрек»:

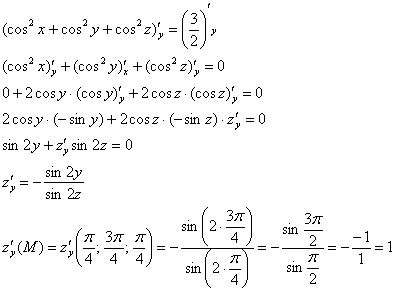
Ответ:

Для самостоятельного решения:

Пример 5

Вычислить значения частных производных функции  в точке .

Примеры № 4, 5 взяты из задачника Рябушко и желающие могут раздобыть там ещё около 30 примеров (ИДЗ 10.1), кстати, с правильными ответами!

На практике вам могут предложить похожую задачу, но не с точкой, которая принадлежит самой поверхности, а с точкой  из плоскости . В этом случае значение  придётся отыскать самостоятельно. Например, если дана функция  и точка , то выполняем подстановку :
, откуда следует, что .

Частные производные неявно заданной функции трёх переменных

Задачка редкая, но пропускать не стОит. Советую сделать перерыв после предыдущего параграфа (особенно, если вы что-то порешали), поскольку в функции трёх переменных  буква «зет» – уже независимая переменная, и по этой причине вас будет неслабо подглючивать.

Всё очень похоже – разве что аргумент один прибавился. Неявно заданную функцию трёх переменных обычно обозначают через , и её дифференцирование осуществляется по тем же принципам:

Пример 6

Найти частные производные первого порядка функции

Решение: итак, требуется найти , способ первый, «классический»:

Найдём частную производную по «икс»:

Что тут нужно держать на заметке?  и  – это «живые» буквы, а  – константы:

Собираем слагаемые с производной в левой части и выражаем результат:

Найдём частную производную по «игрек» ( – константы):

В левой части дела заметно усложнились:

Распишу всё максимально подробно:

Таким образом:

Это была, пожалуй, наиболее трудная производная.

И, наконец, навешиваем на обе части «зетовые» штрихи ( – константы):

Теперь способ второй, по пожеланиям учащихся. Берём исходное уравнение , переносим все слагаемые в одну часть:  и рассматриваем функцию четырёх переменных . Тогда наши частные производные отыскиваются по следующим формулам:

Когда мы находим производную по какой-либо переменной, то три другие переменные считаются константами:

Таким образом:

Решать можно и так, и так, а ещё лучше – обоими способами, дабы выполнить проверку.

Ответ:

И чисто символическое заключительное задание для самостоятельной работы:

Пример 7

Найти частные производные первого порядка неявно заданной функции

В образце я решил задачу 1-м способом, и вас есть увлекательная возможность повторить мой путь. И, конечно же, протестируйте способ 2-й , выполним тем самым проверку.

Надеюсь, к концу статьи вы сохранили форму и бодрое расположение духа, потому что высшая математика ещё потребует некоторых затрат энергии =)

Жду вас на новых уроках!

Решения и ответы:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте