Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Уравнения в высшей математике

Данный урок наряду с материалами о множествах, векторах, графиках и т.д. носит общеобразовательный характер и имеет большое значение для изучения ВСЕГО курса высшей математики. Сегодня мы повторим «школьные» уравнения, но не просто «школьные» – а те из них, которые повсеместно встречаются в различных задачах вышмата. Как обычно, повествование пойдёт в прикладном ключе, т.е. я не буду заострять внимание на определениях, классификациях, а поделюсь с вами именно личным опытом решения. Информация предназначена, прежде всего, для начинающих, но и более подготовленные читатели тоже найдут для себя немало интересных моментов. И, конечно же, будет новый материал, выходящий за рамки средней школы. 
 
Итак, уравнение…. Многие с содроганием вспоминают это слово. Чего только стОят «навороченные» уравнения с корнями... …забудьте о них! Потому что дальше вам будут встречаться самые безобидные «представители» этого вида. Или занудные тригонометрические уравнения с десятками методов решения. Если честно, я и сам их не особо любил…. Без паники! – далее вас ожидают преимущественно «одуванчики» с очевидным решением в 1-2 шага. Хотя и «репейник», безусловно, цепляется – здесь нужно быть объективным.

Как ни странно, в высшей математике гораздо чаще приходится иметь дело с совсем примитивными уравнениями наподобие линейного уравнения .

Что значит решить это уравнение? Это значит – найти ТАКОЕ значение «икс» (корень), которое обращает его в верное равенство. Перебросим «тройку» направо со сменой знака:

и сбросим «двойку» в правую часть (или, то же самое – умножим обе части на ):

Для проверки подставим завоёванный трофей в исходное уравнение :

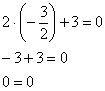
Получено верное равенство, значит, найденное значение  действительно является корнем данного уравнения. Или, как ещё говорят, удовлетворяет данному уравнению.

Обратите внимание, что корень можно записать и в виде десятичной дроби:  
И постарайтесь не придерживаться этого скверного стиля! Причину я повторял неоднократно, в частности, на первом же уроке по высшей алгебре.

Кстати, уравнение можно решить и «по-арабски»:

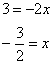
И что самое интересное – данная запись полностью легальна! Но если Вы не преподаватель, то так лучше не делать, ибо оригинальность здесь наказуема =)

А теперь немного о

графическом методе решения

Уравнение  имеет вид  и его корень – есть «иксовая» координата точки пересечения графика линейной функции  с графиком линейной функции  (осью абсцисс):

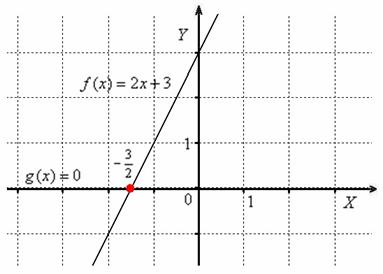
Казалось бы, пример настолько элементарен, что разбирать тут больше нечего, однако из него можно «выжать» ещё один неожиданный нюанс: представим то же самое уравнение в виде  и построим графики функций :

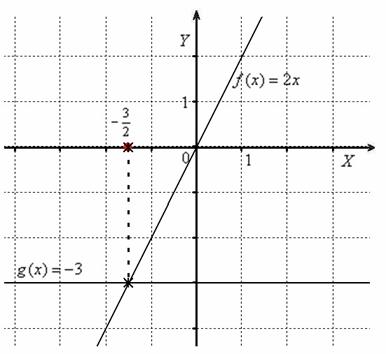
При этом, пожалуйста, не путайте два понятия: уравнение – это уравнение, а функция – это функция! Функции лишь помогают найти корни уравнения. Коих может быть два, три, четыре и даже бесконечно много. Ближайшим примером в этом смысле является всем известно квадратное уравнение, алгоритм решения которого удостоился отдельного пункта «горячих» школьных  формул. И это не случайно! Если вы умеете решать квадратное уравнение и знаете теорему Пифагора, то, можно сказать, «пол высшей математики уже в кармане» =) Преувеличено, конечно, но и не так далеко от истины!

А поэтому не поленимся и прорешаем какое-нибудь квадратное уравнение по стандартному алгоритму:

, значит, уравнение имеет два различных действительных корня:

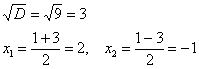
Легко убедиться, что оба найденных значения действительно удовлетворяют данному уравнению:

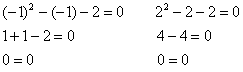
Что делать, если вы вдруг позабыли алгоритм решения, и под рукой нет средств/рук помощи? Такая ситуация может возникнуть, например, на зачёте или экзамене. Используем графический метод! И тут есть два пути: можно поточечно построить параболу , выяснив тем самым, где она пересекает ось  (если пересекает вообще). Но лучше поступить хитрее: представим уравнение в виде , начертим графики более простых функций  – и «иксовые» координаты их точек пересечения, как на ладони!

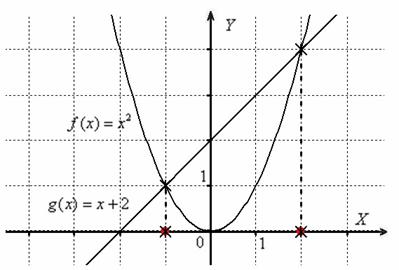
Если окажется, что прямая касается параболы, то уравнение имеет два совпавших (кратных) корня. Если окажется, что прямая не пересекает параболу, значит, действительных корней нет.

Для этого, конечно, нужно уметь строить графики элементарных функций, но с другой стороны эти умения по силам даже школьнику.

И вновь – уравнение  – это уравнение, а функции ,  – это функции, которые лишь помогли решить уравнение!

И тут, кстати, уместно будет вспомнить ещё одну вещь: если все коэффициенты уравнения умножить на ненулевое число, то его корни не изменятся.

Так, например, уравнение  имеет те же самые корни. В качестве простейшего «доказательства» вынесу константу за скобки:
 и безболезненно её уберу (разделю обе части на «минус два»):

НО! Если мы рассматриваем функцию , то здесь уже избавляться от константы нельзя! Допустимо разве что вынесение множителя за скобки: .

Многие недооценивают графический метод решения, считая его чем-то «несолидным», а некоторые и вовсе забывают о такой возможности. И это в корне ошибочно, поскольку построение графиков иногда просто спасает ситуацию!

Ещё один пример: предположим, вы не помните корни простейшего тригонометрического уравнения: . Общая формула есть в школьных учебниках, во всех справочниках по элементарной математике, но они вам недоступны. Однако решить уравнение критически важно (иначе «двойка»). Выход есть! – строим графики функций :

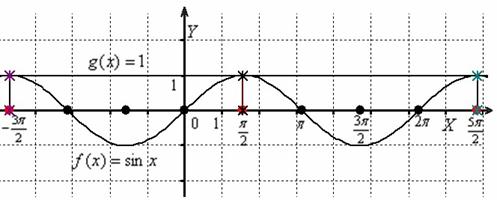
после чего спокойненько записываем «иксовые» координаты их точек пересечения:

Корней бесконечно много и в алгебре принята их свёрнутая запись:
, где  ( – множество целых чисел).

И, не «отходя от кассы», пару слов о графическом методе решения неравенств с одной переменной. Принцип такой же. Так, например, решением неравенства   является любое «икс», т.к. синусоида почти полностью лежит под прямой . Решением неравенства  является множество промежутков, на которых куски синусоиды лежат строго выше прямой  (оси абсцисс):

или, если короче:

А вот множество решений неравенства  – пусто, поскольку никакая точка синусоиды не лежит выше прямой .

Что-нибудь не понятно? Срочно штудировать уроки о множествах и графиках функций!

Разминаемся:

Задание 1

Решить графически следующие тригонометрические уравнения:

Ответы внизу страницы (не подсматриваем!)

Как видите, для изучения точных наук совсем не обязательно зубрить формулы и справочники! И более того, это принципиально порочный подход.

Как я уже обнадёжил вас в самом начале урока, сложные тригонометрические уравнения в стандартном курсе высшей математики приходится решать крайне редко. Вся сложность, как правило, заканчивается уравнениями вроде , решением которого являются две группы корней, происходящие от простейших уравнений  и . С решением последнего сильно не парьтесь – посмотрите в книжке или найдите в Интернете =)

Графический метод решения может выручить и в менее тривиальных случаях. Рассмотрим, например, следующее «разношёрстное» уравнение:

Перспективы его решения выглядят... вообще никак не выглядят, однако стОит только представить уравнение в виде , построить графики функций  и всё окажется невероятно просто. Чертёж есть в середине статьи о бесконечно малых функциях (откроется на соседней вкладке).

Тем же графическим методом можно выяснить, что  уравнение  имеет уже два корня, причём один из них равен нулю, а другой, судя по всему, иррационален и принадлежит отрезку . Данный корень можно вычислить приближённо, например, методом касательных. Кстати, в некоторых задачах, бывает, требуется не отыскать корни, а выяснить, есть ли они вообще. И здесь тоже может помочь чертёж – если графики не пересекаются, то корней нет.

Переходим ко второй части урока:

Рациональные корни многочленов с целыми коэффициентами. Схема Горнера

Решения и ответы:

Задание 1 Ответы:
а) решений нет (синусоида не пересекается с прямой )

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте