


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Разложение функций в степенные ряды.
Ряд Тейлора. Ряд Маклорена. Примеры решений
Продолжаем рассматривать теорию и практику степенных рядов. Материал несложный, но для его понимания необходимо уже более или менее хорошо ориентировать в теме. Если Вы только-только приступили к изучению рядов или чувствуйте себя чайником, пожалуйста, начните с урока Ряды для чайников. Примеры решений. Далее следует прочитать статью Степенные ряды. Область сходимости ряда, в частности, Вы должны хорошо понимать, что такое степенной ряд и его область сходимости. А для целей сегодняшнего урока потребуется методический материал Таблица разложений некоторых функций в степенные ряды, его можно раздобыть в кладовке Математические формулы и таблицы. По возможности, таблицу лучше распечатать, поскольку она потребуется не только сейчас, но и в оффлайне.
Понятие суммы степенного ряда
Начнем подходить к теме с воспоминаний. Как мы помним, любой числовой ряд может или сходиться, или расходиться. Если числовой ряд ![]() сходится, то это значит, что сумма его членов равна некоторому конечному числу:
сходится, то это значит, что сумма его членов равна некоторому конечному числу: ![]()
На уроке Степенные ряды. Область сходимости ряда мы рассматривали уже не числовые, а функциональные и степенные ряды. Возьмём тот самый подопытный степенной ряд, который всем понравился: ![]() . В ходе исследования было установлено, что этот ряд сходится при
. В ходе исследования было установлено, что этот ряд сходится при ![]() . Если числовые ряды сходятся к ЧИСЛАМ, то к чему же сходятся функциональные и степенные ряды? Правильно подумали. Функциональные ряды сходятся к ФУНКЦИЯМ. В частности, суммой ряда
. Если числовые ряды сходятся к ЧИСЛАМ, то к чему же сходятся функциональные и степенные ряды? Правильно подумали. Функциональные ряды сходятся к ФУНКЦИЯМ. В частности, суммой ряда ![]() в его области сходимости
в его области сходимости ![]() является некоторая функция
является некоторая функция ![]() :
:
![]()
Еще раз подчеркиваю, что данный факт справедлив только для найденной области ![]() , вне этого промежутка степенной ряд
, вне этого промежутка степенной ряд ![]() будет расходиться.
будет расходиться.
Чтобы всё стало окончательно понятно, рассмотрим примеры с картинками. Я выпишу простейшее табличное разложение синуса в степенной ряд:
![]()
Область сходимости ряда: ![]()
(По какому принципу получены сами элементарные табличные разложения, мы рассмотрим чуть позже).
Теперь вспоминаем школьный график синуса ![]() :
:

Вот такая симпатичная синусоида. Хмм…. Где-то я уже это видел….
Теперь фишка. Если начертить график бесконечного многочлена ![]() , то получится… та же самая синусоида! То есть, наш степенной ряд
, то получится… та же самая синусоида! То есть, наш степенной ряд ![]() сходится к функции
сходится к функции ![]() . Используя признак Даламбера (см. статью Степенные ряды. Область сходимости ряда), легко проверить, что ряд
. Используя признак Даламбера (см. статью Степенные ряды. Область сходимости ряда), легко проверить, что ряд ![]() сходится при любом «икс»:
сходится при любом «икс»: ![]() (собственно, поэтому в таблице разложений и появилась такая запись об области сходимости).
(собственно, поэтому в таблице разложений и появилась такая запись об области сходимости).
А что значит вообще «сходится»? По смыслу глагола – что-то куда-то идёт. Если я возьму первые три члена ряда ![]() и начерчу график многочлена пятой степени, то он лишь отдаленно будет напоминать синусоиду. А вот если составить многочлен из первых ста членов ряда:
и начерчу график многочлена пятой степени, то он лишь отдаленно будет напоминать синусоиду. А вот если составить многочлен из первых ста членов ряда: ![]() и начертить его график, то он будет с синусоидой практически совпадать (на достаточно длинном промежутке). Чем больше членов ряда – тем лучше приближение. И, как уже отмечалось, график бесконечного многочлена – есть в точности синусоида. Иными словами, ряд
и начертить его график, то он будет с синусоидой практически совпадать (на достаточно длинном промежутке). Чем больше членов ряда – тем лучше приближение. И, как уже отмечалось, график бесконечного многочлена – есть в точности синусоида. Иными словами, ряд ![]() сходится к функции
сходится к функции ![]() при любом значении «икс».
при любом значении «икс».
Рассмотрим более печальный пример, табличное разложение арктангенса:
![]()
Область сходимости ряда: ![]()
Печаль заключается в том факте, что график бесконечного многочлена ![]() существует и совпадает с графиком арктангенса
существует и совпадает с графиком арктангенса ![]() только на отрезке
только на отрезке ![]() (т.е. в области сходимости ряда):
(т.е. в области сходимости ряда):
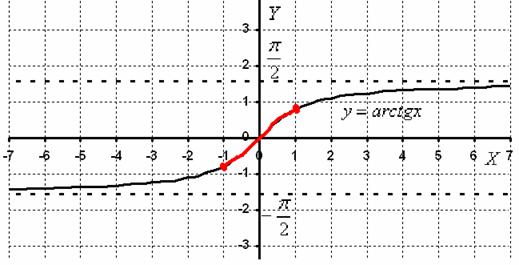
Вне отрезка ![]() разложение арктангенса в ряд
разложение арктангенса в ряд ![]() расходится, и о графике речи не идёт вообще, поскольку каждое значение бесконечного многочлена бесконечно .
расходится, и о графике речи не идёт вообще, поскольку каждое значение бесконечного многочлена бесконечно .
Исходя из вышесказанного, можно сформулировать две взаимно обратные задачи:
– найти сумму ряда (функцию) по известному разложению;
– разложить функцию в ряд (если это возможно) и найти область сходимости ряда.
Что проще? Конечно же, разложение – с него и начнём. После чего я рекомендую не затягивать и в ближайшие часы-дни (пока свежи воспоминания) потренироваться в нахождении суммы степенного ряда.
Разложение функций в степенной ряд.
Ряд Тейлора. Ряд Маклорена
Приступим к увлекательному занятию – разложению различных функций в степенные ряды. Сначала пара формул, затем практические задания.
Если функция ![]() в некотором интервале раскладывается в степенной ряд по степеням
в некотором интервале раскладывается в степенной ряд по степеням ![]() , то это разложение единственно и задается формулой:
, то это разложение единственно и задается формулой:
![]()
Примечания: надстрочный индекс ![]() в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву
в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву ![]() .
.
Данная формула носит фамилию англичанина Тейлора (ударение на первый слог).
На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда ![]() :
:
![]()
Этот ряд получил известность благодаря шотландцу Маклорену (ударение на второй слог). Разложение Маклорена также называют разложением Тейлора по степеням ![]() .
.
Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции:
![]()
Как оно получилось? По формуле Маклорена:
![]()
Рассмотрим функцию ![]() , тогда:
, тогда:
![]()
Теперь начинаем находить производные в точке ![]() : первую производную, вторую производную, третью производную и т.д. Это просто, поскольку при дифференцировании экспонента превращается в саму себя:
: первую производную, вторую производную, третью производную и т.д. Это просто, поскольку при дифференцировании экспонента превращается в саму себя:
![]()
![]()
![]()
![]()
![]()
![]()
И так далее….
Совершенно очевидно, что ![]()
Подставляем единицы в формулу Маклорена и получаем наше табличное разложение!
Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).
Примеры разложения функций в ряд Маклорена
В данном параграфе мы рассмотрим типовую задачу на разложение функции в ряд Маклорена и определении области сходимости полученного ряда. Нет, мучаться с нахождением производных не придется, мы будем пользоваться таблицей.
Пример 1
Разложить функцию в ряд Маклорена. Найти область сходимости полученного ряда.
! Эквивалентная формулировка: Разложить функцию в ряд по степеням ![]()
![]()
Решение незамысловато, главное, быть внимательным.
Конструируем наш ряд. Плясать начинают, как правило, от функции, разложение которой есть в таблице:
![]() .
.
В данном случае ![]() :
:
![]()
Раскрываем наверху скобки:
![]()
Теперь умножаем обе части на «икс»:
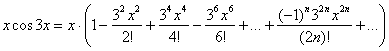
В итоге искомое разложение функции в ряд:
![]()
Как определить область сходимости? Чем постоянно проводить очевидные рассуждения, проще запомнить: разложения синуса, косинуса и экспоненты сходятся при любом действительном значении ![]() (за исключением, конечно, тех случаев, когда, например,
(за исключением, конечно, тех случаев, когда, например, ![]() – см. комментарии к табличным разложениям). Домножение
– см. комментарии к табличным разложениям). Домножение ![]() на «икс» не играет никакой роли в плане сходимости, поэтому область сходимости полученного ряда:
на «икс» не играет никакой роли в плане сходимости, поэтому область сходимости полученного ряда: ![]()
Пример 2
Разложить функцию в ряд по степеням ![]() . Найти область сходимости ряда.
. Найти область сходимости ряда.
![]()
Это пример для самостоятельного решения.
Я не стал рассматривать простейшие разложения вроде ![]() ,
, ![]() или
или ![]() , поскольку это фактически задача в одно действие. В нужные табличные разложения вместо «альфы» необходимо подставить
, поскольку это фактически задача в одно действие. В нужные табличные разложения вместо «альфы» необходимо подставить ![]() ,
, ![]() ,
, ![]() и немного причесать полученные ряды. Единственное предостережение – не теряйте по невнимательности степени и знаки.
и немного причесать полученные ряды. Единственное предостережение – не теряйте по невнимательности степени и знаки.
А сейчас для разнообразия рассмотрим что-нибудь с минусами.
Пример 3
Разложить функцию в ряд по степеням ![]() . Найти область сходимости ряда.
. Найти область сходимости ряда.
![]()
В таблице находим похожее разложение:
![]()
Трюк прост – перепишем нашу функцию немного по-другому:
![]()
Таким образом, ![]() и:
и:
![]()
Окончательно:
![]()
Теперь нужно определить область сходимости. Согласно таблице, ряд сходится при ![]() .
.
В данном случае ![]() :
:
![]()
Так как квадрат неотрицателен, то при раскрытии модуля знак «минус» просто испаряется:
![]()
Исследуем сходимость ряда на концах найденного интервала. Значения ![]() ,
, ![]() не входят в область определения функции
не входят в область определения функции ![]() , но как мы видели в Примере 2, в «проблемной» точке САМ РЯД сходиться может. И поэтому от греха подальше лучше выполнить прямую подстановку концов интервала в найденное разложение. При
, но как мы видели в Примере 2, в «проблемной» точке САМ РЯД сходиться может. И поэтому от греха подальше лучше выполнить прямую подстановку концов интервала в найденное разложение. При ![]() получаем:
получаем: ![]() – расходящийся гармонический ряд. И он же получается при
– расходящийся гармонический ряд. И он же получается при ![]()
Таким образом, область сходимости ряда:
![]()
Но так бывает далеко не всегда:
Простейшее разложение из учебника ![]() сходится ещё в одной точке:
сходится ещё в одной точке: ![]() . Здесь значение
. Здесь значение ![]() тоже вне игры, а вот при
тоже вне игры, а вот при ![]() сумма получившегося знакочередующегося ряда
сумма получившегося знакочередующегося ряда ![]() в точности равна
в точности равна ![]() .
.
Интересно отметить, что разложение в ряд такого логарифма:
![]() – сходится уже на обоих концах интервала:
– сходится уже на обоих концах интервала: ![]() (при подстановках
(при подстановках ![]() ,
, ![]() получается тот же самый сходящийся ряд
получается тот же самый сходящийся ряд ![]() )
)
Таким образом, с логарифмами нужно работать осмотрительно!
Пара примеров для самостоятельного решения:
Пример 4
Разложить функцию в ряд по степеням ![]() . Найти область сходимости ряда.
. Найти область сходимости ряда.
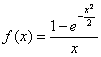
Пляска традиционно начинается от «главной» функции, то есть, начинать нужно с экспоненты.
Пример 5
Разложить функцию в ряд по степеням ![]() . Найти область сходимости ряда.
. Найти область сходимости ряда.
![]()
Здесь разложение не такое сложное, но могут возникнуть трудности с нахождением области сходимости полученного ряда.
Полные решения и ответы в конце урока.
Не редкость, когда перед разложением функции в ряд её необходимо предварительно преобразовать. Канонический случай – это разложение функции ![]() . Перед тем как ее раскладывать в ряд, необходимо понизить степень с помощью известной тригонометрической формулы:
. Перед тем как ее раскладывать в ряд, необходимо понизить степень с помощью известной тригонометрической формулы: ![]() . Решать я этот пример не буду, поскольку он довольно простой, к тому же что-то подобное мы недавно рассмотрели.
. Решать я этот пример не буду, поскольку он довольно простой, к тому же что-то подобное мы недавно рассмотрели.
Пример 6
Разложить функцию в ряд по степеням ![]() . Найти область сходимости ряда.
. Найти область сходимости ряда.
![]()
Смотрим в таблицу и находим наиболее похожее разложение:
![]()
Во-первых, вверху должна быть единица, поэтому представляем нашу функцию в виде произведения: ![]()
Теперь нам нужно в знаменателе устроить ![]() , для этого выносим двойку за скобки:
, для этого выносим двойку за скобки:
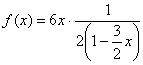
И сокращаем на два:
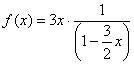
В данном случае ![]() , таким образом:
, таким образом:
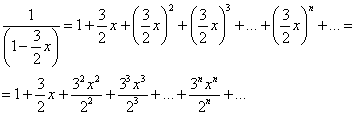
В итоге искомое разложение:
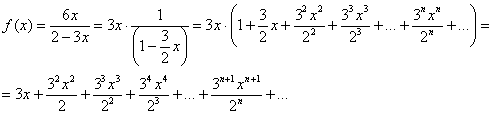
Определим область сходимости ряда. Можно пойти длинным и надежным путем – использовать признак Даламбера для полученного степенного ряда ![]() , т.е. найти интервал сходимости и т.д. Но можно поступить проще. В таблице указано, что биномиальный ряд сходится при
, т.е. найти интервал сходимости и т.д. Но можно поступить проще. В таблице указано, что биномиальный ряд сходится при ![]() . В данном случае
. В данном случае ![]() , поэтому:
, поэтому:
![]()
Умножаем все части неравенства на ![]() :
:
![]() – интервал сходимости полученного ряда.
– интервал сходимости полученного ряда.
Что происходит с рядом ![]() на концах интервала?
на концах интервала?
При ![]() получаем:
получаем: 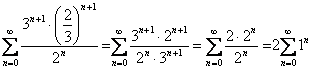 – данный ряд расходится, т.к. не выполнен необходимый признак сходимости,
– данный ряд расходится, т.к. не выполнен необходимый признак сходимости,
и при:  – расходится по той же причине.
– расходится по той же причине.
Таким образом, область сходимости полученного ряда: ![]()
Пример 7
Разложить функцию в ряд по степеням ![]() . Найти область сходимости ряда.
. Найти область сходимости ряда.
![]()
Указание: предварительно функцию следует упростить, используя свойство логарифмов: ![]()
Это пример для самостоятельного решения.
Разложение функций в ряд Маклорена необходимо проводить и в ряде других задач, например, в задаче приближенного вычисления определенного интеграла. Кстати, там, помимо нового материала, можно посмотреть примеры других разложений, которые не поместились в этот урок.
Примеры разложения функций в ряд Тейлора по степеням 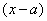 , когда
, когда 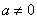
Данное задание является более сложным и встречается значительно реже, но всё-таки 2-3 примера не помешают. Пригодится.
Вытащим из чулана общую формулу Тейлора:
![]()
Еще раз повторю, что вместо буквы «а» на практике часто можно встретить букву ![]() .
.
В чём сложность разложения функции по степеням ![]() при ненулевом значении «а»? Сложность состоит в том, что нам не удастся воспользоваться табличными разложениями, и придётся самостоятельно находить и вычислять производные. Или не придётся. Но сначала разберём универсальный «классический» метод с производными.
при ненулевом значении «а»? Сложность состоит в том, что нам не удастся воспользоваться табличными разложениями, и придётся самостоятельно находить и вычислять производные. Или не придётся. Но сначала разберём универсальный «классический» метод с производными.
Очень хорошо если вы проработали урок Производные высших порядков, впрочем, я постараюсь максимально подробно закомментировать оставшиеся задачи.
И сразу небольшой Пример 8
Разложить функцию ![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням ![]()
В данном случае ![]() , смотрим на формулу Тейлора, и становится уже всё понятнее.
, смотрим на формулу Тейлора, и становится уже всё понятнее.
Теперь предстоит ручная работа по конструированию разложения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , все производные, начиная с четвёртой производной, будут нулевыми.
, все производные, начиная с четвёртой производной, будут нулевыми.
Теперь подставляем весь найденный скарб в формулу Тейлора:
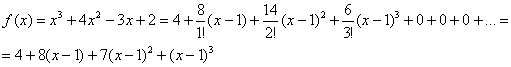
Готово. Для проверки можно раскрыть скобки:
![]()
Получен исходный многочлен, что и требовалось проверить.
Рассмотрим более содержательные примеры.
Пример 9
Разложить функцию ![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням ![]() . Найти область сходимости полученного ряда.
. Найти область сходимости полученного ряда.
Решение: Используем разложение функции в ряд Тейлора по степеням ![]()
![]()
Хех, опять предстоит ручная работа….
В данном случае: ![]()
![]()
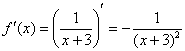
![]()
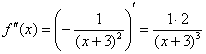
![]()
Замечаем, что с такими раскладами производные можно находить до бесконечности. Поэтому необходимо уловить некоторую закономерность. Найдем ещё третью производную:
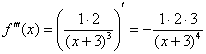
![]()
А теперь проанализируем найденные производные:
![]() ,
, ![]() ,
, ![]() .
.
Закономерность прослеживается: знаки чередуются, в числителе накручивается факториал, а в знаменателе растёт степень.
Теперь, исходя из выявленной закономерности, нужно составить производную «энного» порядка. В данном случае она выглядит так:
![]()
Как проверить, правильно ли составлена энная производная? Подставьте в неё значения ![]() ,
, ![]() ,
, ![]() и у вас должны получиться в точности первая, вторая и третья производные. После того, как мы убедились в том, что энная производная составлена правильно, подставляем в неё наше значение:
и у вас должны получиться в точности первая, вторая и третья производные. После того, как мы убедились в том, что энная производная составлена правильно, подставляем в неё наше значение:
![]()
Теперь осталось все труды подставить в формулу Тейлора и аккуратно провести упрощения:
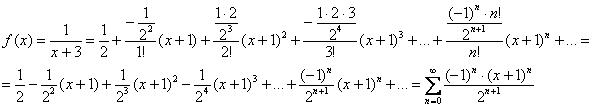
Далее необходимо найти область сходимости полученного степенного ряда ![]() . Это стандартная задача, которую мы многократно прорешивали на уроке Степенные ряды. Область сходимости ряда. Впрочем, из того соображения, что на концах интервала должны сократиться «двойки в степени эн», ответ нетрудно «углядеть» и устно:
. Это стандартная задача, которую мы многократно прорешивали на уроке Степенные ряды. Область сходимости ряда. Впрочем, из того соображения, что на концах интервала должны сократиться «двойки в степени эн», ответ нетрудно «углядеть» и устно: ![]() .
.
Теперь способ второй. Он основан на замене переменной. Итак, требуется разложить ту же функцию ![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням ![]() , и мы проводим замену:
, и мы проводим замену:
![]() , откуда выражаем
, откуда выражаем ![]() – и подставляем в нашу функцию:
– и подставляем в нашу функцию:
![]()
при этом общая формула Тейлора превращается в формулу Маклорена:
![]()
и появляется возможность воспользоваться теми же табличными разложениями!
Таким образом, наша задача свелась к задаче предыдущего параграфа, представим полученную функцию в виде:
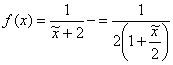 и воспользуемся разложением:
и воспользуемся разложением:
![]() ., в данном случае
., в данном случае ![]() :
:
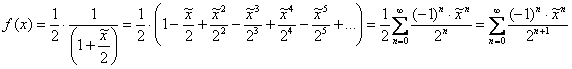 , после чего вспоминаем о том, что
, после чего вспоминаем о том, что ![]() и записываем искомое разложение:
и записываем искомое разложение:
![]() , и проверочка заодно получилась.
, и проверочка заодно получилась.
Возникает вопрос: а зачем тогда возиться с производными? И ответ здесь такой: замена далеко не всегда приводит к желаемому результату, так, например, она совершенно бесполезна в Примере 8, и ещё много для каких функций. Поэтому главным и основополагающим методом следует считать прямое построение ряда через производные.
Заключительный пример для самостоятельного решения:
Пример 10
Разложить функцию ![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням ![]() . Найти область сходимости полученного ряда.
. Найти область сходимости полученного ряда.
В образце приведены оба способа решения.
Как ваш тонус? Я так и знал, что на высоте! – поэтому самое время потренироваться в нахождении сумм степенных рядов по известным разложениям. Кроме того, на следующем уроке много интересной и... неожиданной информации. Только не злоупотребляйте =)
Желаю успехов!
Решения и ответы:
Пример 2: Решение: используем разложение: ![]() .
.
В данном случае ![]()
![]()
![]()
Область сходимости ряда: ![]() .
.
! Примечание: здесь может сложиться впечатление, что из области сходимости ряда следует исключить точку ![]() , которая не входит в область определения функции, однако тут речь идёт об области сходимости ряда. А полученный ряд преспокойно сходится в точке
, которая не входит в область определения функции, однако тут речь идёт об области сходимости ряда. А полученный ряд преспокойно сходится в точке ![]() – но не к исходной функции, а к изолированному значению:
– но не к исходной функции, а к изолированному значению: ![]() . Интересно отметить, что здесь функция терпит устранимый разрыв:
. Интересно отметить, что здесь функция терпит устранимый разрыв: ![]() и сумма степенного ряда непрерывна.
и сумма степенного ряда непрерывна.
Пример 4: Решение: используем разложение: ![]() .
.
В данном случае ![]()
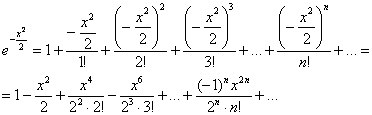
Конструируем функцию дальше:
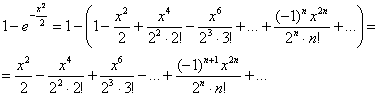
Окончательно:
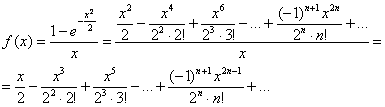
Ряд сходится при ![]()
Примечание: в точке ![]() ряд сходится не к исходной функции, а к нулю:
ряд сходится не к исходной функции, а к нулю: ![]()
Пример 5: Решение: используем частный случай биномиального разложения:
![]()
В данном случае ![]()
Таким образом:
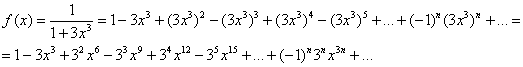
Само по себе разложение не слишком сложное, важно правильно найти область сходимости полученного ряда. Есть длинный путь и есть короткий.
Путь короткий: биномиальный ряд сходится при ![]() (см. таблицу).
(см. таблицу).
В данном случае ![]() :
:
![]() .
.
Делим все части на 3 и извлекаем из всех частей кубический корень:
![]()
![]() – интервал сходимости ряда.
– интервал сходимости ряда.
Исследуем сходимость нашего ряда ![]() на концах найдённого интервала:
на концах найдённого интервала:
при ![]() получаем ряд:
получаем ряд: 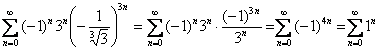 ,
,
и на правом конце: 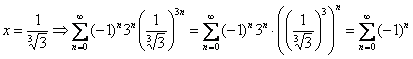
Оба числовых ряда расходятся, так как не выполнен необходимый признак сходимости рядов.
Таким образом, область сходимости ряда: ![]()
Путь длинный (но более надежный и универсальный) состоит в исследовании полученного ряда ![]() с помощью признака Даламбера по стандартной схеме, рассмотренной на уроке Степенные ряды. Область сходимости ряда.
с помощью признака Даламбера по стандартной схеме, рассмотренной на уроке Степенные ряды. Область сходимости ряда.
Пример 7: Решение: преобразуем функцию:
![]()
Используем разложение:
![]()
В данном случае ![]()
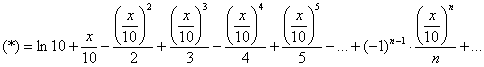
Таким образом:
![]()
Или в свёрнутом виде: ![]()
Найдем область сходимости полученного степенного ряда. Согласно таблице, использованное разложение сходится при ![]() . В данном случае
. В данном случае ![]() , поэтому:
, поэтому:
![]()
![]() – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость ряда на концах найденного интервала:
при ![]() – расходится;.
– расходится;.
при ![]() – сходится по признаку Лейбница, условно.
– сходится по признаку Лейбница, условно.
Таким образом, область сходимости полученного степенного ряда: ![]()
Пример 10: Решение, способ первый: Используем разложение функции в ряд Тейлора по степеням ![]() :
:
![]()
В данном случае: ![]()
![]()
![]()
![]()
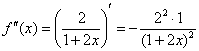
![]()
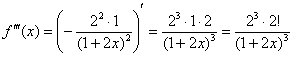
![]()
…
![]()
![]()
…
Таким образом:
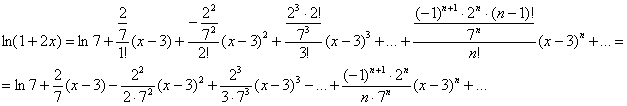 Область сходимости полученного степенного ряда уже надоела =)
Область сходимости полученного степенного ряда уже надоела =)
Ответ:
![]()
ряд сходится при ![]() .
.
Способ второй: проведём замену ![]() , выразим
, выразим ![]() – и подставим в функцию:
– и подставим в функцию:
![]()
Используем разложение ![]() , в данной задаче
, в данной задаче ![]() :
:
![]()
обратная замена ![]() :
:
![]() – искомое разложение.
– искомое разложение.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright