


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Криволинейные интегралы. Понятие и примеры решений
Жизнь такова, что из любой новой темы (не обязательно научной) пытливый человеческий ум стремится «выжать» по максимуму – все идеи и все возможности. Появилось понятие вектора, и, пожалуйста – курс аналитической геометрии не заставил себя ждать. А также дифференциальная геометрия, теории поля и прочие гранитные плиты для зубов разной крепости. Пришла наука к понятию производной – …ну, думаю, тут объяснять не нужно! …некоторые до сих пор отойти не могут =)
И интегралы тоже не стали исключением из этого правила. Давайте посмотрим на криволинейную трапецию и вспомним классическую схему интегрального исчисления:
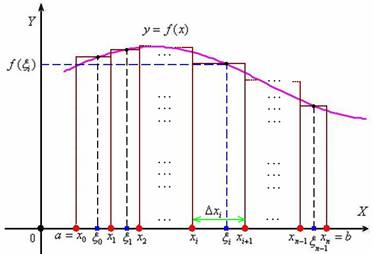
– отрезок ![]() дробится на части;
дробится на части;
– составляется интегральная сумма, которая равна площади ступенчатой фигуры;
– и, наконец, количество отрезков разбиения устремляется к бесконечности – в результате чего эта фигура превращается в криволинейную трапецию площади 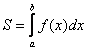 .
.
Аналогично выводятся формулы объема тела вращения, длины дуги кривой и др.
Более того, наводящие ужас кратные интегралы «устроены» принципиально так же – по существу, они отличается только областью интегрирования: у двойных интегралов – это не отрезок, а плоская фигура, у тройных – пространственное тело.
И, чтобы у вас сразу отлегло от сердца – наши «сегодняшние» криволинейные интегралы далеки от «ужаса», они больше похожи на «обычные» кошмары интегралы. Уже из самого названия нетрудно догадаться, что областью интегрирования таких интегралов являются кривые линии (но иногда полностью либо частично – прямые).
На уроке о пределе функции двух переменных я придумал реалистичную модель, которая снискала большую популярность – да такую, что там каждый день собираются целые экскурсии =) Итак, паркет вашей комнаты – это координатная плоскость ![]() , в углу стоит ось
, в углу стоит ось ![]() , а вверху «зависло» расправленное одеяло, заданное функцией
, а вверху «зависло» расправленное одеяло, заданное функцией ![]() .
.
Возьмите в руки мел и начертите на полу под одеялом произвольную кривую ![]() . Как вариант, у неё могут быть «острые углы» – такая линия называется кусочно-гладкой. Можно изобразить даже ломаную. ВажнА спрямляемость (см. урок о методах Эйлера) и непрерывность пути интегрирования. Теперь суть:
. Как вариант, у неё могут быть «острые углы» – такая линия называется кусочно-гладкой. Можно изобразить даже ломаную. ВажнА спрямляемость (см. урок о методах Эйлера) и непрерывность пути интегрирования. Теперь суть:
Представьте, что от одеяла осталась всего лишь одна нитка – лежащая над кривой ![]() . Вертикальная поверхность, расположенная между кривой «эль» и этой «ниткой» представляет собой фрагмент криволинейного цилиндра. Представили? Отлично!
. Вертикальная поверхность, расположенная между кривой «эль» и этой «ниткой» представляет собой фрагмент криволинейного цилиндра. Представили? Отлично!
Криволинейный интеграл первого рода
имеет вид ![]() и по модулю* равен площади
и по модулю* равен площади ![]() данного фрагмента.
данного фрагмента.
* Если график ![]() целиком или бОльшей частью расположен ниже плоскости
целиком или бОльшей частью расположен ниже плоскости ![]() , то площадь получится со знаком «минус».
, то площадь получится со знаком «минус».
Согласно общему принципу интегрирования, произведение бесконечно малого кусочка ![]() кривой
кривой ![]() на соответствующую высоту
на соответствующую высоту ![]() равно бесконечно малому элементу площади данной поверхности:
равно бесконечно малому элементу площади данной поверхности:![]() . А криволинейный интеграл как раз и объединяет эти элементы
. А криволинейный интеграл как раз и объединяет эти элементы ![]() вдоль всей кривой:
вдоль всей кривой: ![]() .
.
! Важно: во многих источниках информации дифференциал дуги кривой ![]() обозначают через
обозначают через ![]() , что, на мой взгляд, не слишком удачный выбор.
, что, на мой взгляд, не слишком удачный выбор.
Если на плоскости ![]() вместо кривой начертить отрезок прямой, то получится не что иное, как плоская криволинейная трапеция, параллельная оси
вместо кривой начертить отрезок прямой, то получится не что иное, как плоская криволинейная трапеция, параллельная оси ![]() . Соответствующий интеграл хоть и каламбурно, но с полным правом можно назвать «прямолинейным».
. Соответствующий интеграл хоть и каламбурно, но с полным правом можно назвать «прямолинейным».
В частности, если подынтегральная функция задаёт плоскость ![]() , то криволинейный интеграл равен площади «ленты» единичной высоты, а также и длине самой линии интегрирования:
, то криволинейный интеграл равен площади «ленты» единичной высоты, а также и длине самой линии интегрирования: ![]() .
.
…Чего только не придумаешь, чтобы не делать чертежей =)
Как вычислить криволинейный интеграл 1-го рода?
Пусть точки ![]() являются концами линии
являются концами линии ![]() , а сама она задана функцией одной переменной
, а сама она задана функцией одной переменной ![]() . Тогда криволинейный интеграл первого рода можно свести к обычному определённому интегралу по следующей формуле:
. Тогда криволинейный интеграл первого рода можно свести к обычному определённому интегралу по следующей формуле:
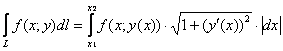
Знак модуля обусловлен природой рассматриваемого интеграла: поскольку дифференциал ![]() не может быть отрицательным (это же элемент длины), то при переходе к определённому интегралу нужно соблюсти статус-кво. В случае «арабского» интегрирования справа налево (когда
не может быть отрицательным (это же элемент длины), то при переходе к определённому интегралу нужно соблюсти статус-кво. В случае «арабского» интегрирования справа налево (когда ![]() ) значения «икс» убывают и поэтому
) значения «икс» убывают и поэтому ![]() – в результате чего появляется побочный минус, подлежащий немедленной ликвидации. Общую формулу можно расписать подробно:
– в результате чего появляется побочный минус, подлежащий немедленной ликвидации. Общую формулу можно расписать подробно:
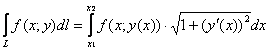 , если
, если ![]() (стандартный случай) или:
(стандартный случай) или:
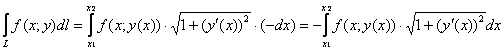 , если
, если ![]() .
.
В частности, при ![]() получается хорошо знакомая формула длины дуги кривой
получается хорошо знакомая формула длины дуги кривой 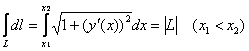 . Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже решали! И теперь вам совсем не нужно решимости:)
. Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже решали! И теперь вам совсем не нужно решимости:)
Пример 1
Вычислить интеграл ![]() от точки
от точки ![]() до точки
до точки ![]() , если кривая
, если кривая ![]() задана уравнением
задана уравнением ![]()
Решение: перед нами каноническое уравнение параболы, и коль скоро в условии дана точка ![]() , то речь идёт о её верхней ветке:
, то речь идёт о её верхней ветке: ![]() .
.
Желающие могут выполнить чертёж. Кстати, вне зависимости от его простоты, иногда это бывает обязательным требованием условия.
В данной задаче имеет место наиболее распространённый случай ![]() , а значит, нужно использовать формулу
, а значит, нужно использовать формулу 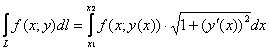 .
.
Сначала удобно найти производную и упростить корень:
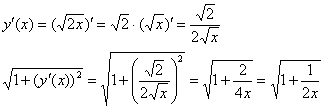
Так как ![]() и
и ![]() , то
, то ![]() – грубо говоря, на данном шаге мы избавляемся от «игреков».
– грубо говоря, на данном шаге мы избавляемся от «игреков».
Предварительная подготовка завершена, пользуемся формулой:
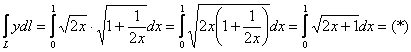
Здесь можно провести замену переменной, но гораздо сподручнее подвести подкоренное выражение под знак дифференциала и обойтись без перехода к новым пределам интегрирования:
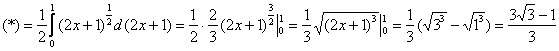
Ответ: ![]()
Если вычислить тот же самый интеграл от точки ![]() до точки
до точки ![]() , то результат не изменится. В этом случае «икс» будет убывать от 1 до 0, следовательно, дифференциал
, то результат не изменится. В этом случае «икс» будет убывать от 1 до 0, следовательно, дифференциал ![]() станет отрицательным и при переходе к определённому интегралу потребуется добавить знак «минус»:
станет отрицательным и при переходе к определённому интегралу потребуется добавить знак «минус»:
![]()
Таким образом, криволинейный интеграл 1-го рода не зависит от направления интегрирования: ![]()
В этой связи типовая задача, как правило, формулируется «нейтрально»: вычислить интеграл ![]() вдоль дуги параболы
вдоль дуги параболы ![]() , расположенной между точками
, расположенной между точками ![]() . Иными словами, совершенно не важно, какая из точек является началом, а какая – концом кривой.
. Иными словами, совершенно не важно, какая из точек является началом, а какая – концом кривой.
Следует отметить, что криволинейный интеграл можно вычислить и другим способом. Поскольку буква «игрек» ничем не хуже «икса», то для вычисления криволинейного интеграла 1-го рода справедлива «зеркальная» формула (тривиальный вариант ![]() ):
):
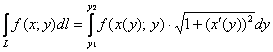 , где
, где ![]() – обратная функция, выражающая линию
– обратная функция, выражающая линию ![]() . В нашей задаче:
. В нашей задаче:
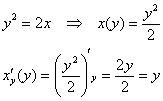
При переходе от ![]() к
к ![]() мы должны избавиться от всех «иксов», однако функция
мы должны избавиться от всех «иксов», однако функция ![]() от них не зависит, а значит, делать ничего не нужно.
от них не зависит, а значит, делать ничего не нужно.
И, учитывая, что для «игрековых» координат точек ![]() справедливо неравенство
справедливо неравенство ![]() , доводим решение до того же самого результата:
, доводим решение до того же самого результата:

В чём состоит геометрический смысл разобранной задачи? На плоскости ![]() между точками
между точками ![]() и
и ![]() находится кусок параболы
находится кусок параболы ![]() , через который проходит «одноимённый» параболический цилиндр
, через который проходит «одноимённый» параболический цилиндр ![]() , «высекающий» из плоскости
, «высекающий» из плоскости ![]() пространственную «ниточку». Криволинейный интеграл
пространственную «ниточку». Криволинейный интеграл ![]() численно равен площади
численно равен площади ![]() фрагмента параболического цилиндра, который расположен между куском параболы и этой «ниткой».
фрагмента параболического цилиндра, который расположен между куском параболы и этой «ниткой».
Как я уже отмечал, криволинейный интеграл может получиться отрицательным – это означает, что фрагмент полностью или бОльшей частью лежит ниже плоскости ![]() . Не удивляйтесь и нулю (в каких случаях?). То есть, «всё как у нормальных интегралов».
. Не удивляйтесь и нулю (в каких случаях?). То есть, «всё как у нормальных интегралов».
Замысловатый пример для самостоятельного решения:
Пример 2
Вычислить площадь фрагмента цилиндрической поверхности ![]() во 2-м и 6-м октантах
во 2-м и 6-м октантах ![]() , который высечен плоскостью
, который высечен плоскостью ![]() и гиперболическим параболоидом
и гиперболическим параболоидом ![]() .
.
Ситуацию крайне важно представить геометрически – надеюсь, на данный момент все знают, как выглядит круговой цилиндр ![]() ; картинку же последней поверхности можно найти в начале урока об экстремумах функций двух и трёх переменных (3-й чертёж). Также будет полезно изобразить на плоскости
; картинку же последней поверхности можно найти в начале урока об экстремумах функций двух и трёх переменных (3-й чертёж). Также будет полезно изобразить на плоскости ![]() кривую интегрирования.
кривую интегрирования.
Краткое решение с комментариями в конце урока – тот, кто правильно во всём разберётся, может считать себя «самоваром» интегралов =)
Довольно часто линия ![]() бывает задана параметрическими уравнениями
бывает задана параметрическими уравнениями ![]() , и в этом случае нужно использовать следующую формулу:
, и в этом случае нужно использовать следующую формулу:
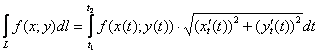 – если значение параметра возрастает
– если значение параметра возрастает ![]() . И для убывающего параметра
. И для убывающего параметра ![]() :
:
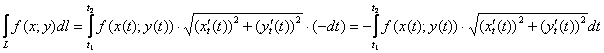
В частности, при ![]() получается опять же знакомая формула длины параметрически заданной кривой:
получается опять же знакомая формула длины параметрически заданной кривой:
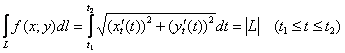
Пример 3
Вычислить криволинейный интеграл ![]() по дуге окружности
по дуге окружности ![]() при изменении параметра
при изменении параметра ![]() .
.
Параметрические уравнения эллипса и окружности я разбирал в тематической статье о площади и объёме, и поэтому если вам не понятен их смысл (или вообще смысл параметрического задания функции), то милости прошу по ссылке.
Решение: указанным пределам изменения параметра соответствует левая верхняя дуга единичной окружности:
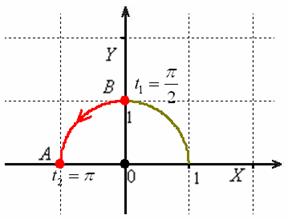
По условию, значение параметра возрастает, поэтому:
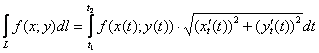
Нет, конечно, можно интегрировать и от ![]() до
до ![]() с добавочным минусом, но зачем?
с добавочным минусом, но зачем?
Как и в предыдущих примерах, сначала удобно найти производные и причесать корень:
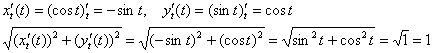
…мда, тут вообще стрижка наголо получилась =)
Итак:

Ответ: ![]()
Два последних примера похожи, как близкие родственники, однако между ними есть существенное различие: в Примере 2 требовалось найти площадь, и поэтому было принципиально важно проанализировать положение поверхности ![]() относительно плоскости
относительно плоскости ![]() . В третьем же примере нужно было вычислить интеграл формально. Как видите, различие здесь точно такое же, как и между вычислением площади с помощью определённого интеграла и «просто» вычислением определённого интеграла.
. В третьем же примере нужно было вычислить интеграл формально. Как видите, различие здесь точно такое же, как и между вычислением площади с помощью определённого интеграла и «просто» вычислением определённого интеграла.
И, разумеется, криволинейные интегралы обладают всеми типичными свойствами «клана интегралов», в частности, для них справедливо свойство линейности:
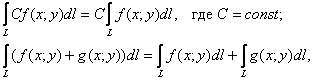
а также свойство аддитивности: если на линии ![]() выбрать промежуточную точку
выбрать промежуточную точку ![]() , то интеграл можно разделить на две части:
, то интеграл можно разделить на две части:
![]()
Или вот такой – более практически важный пример, …сейчас что-нибудь придумаю, чтобы легко было нарисовать в уме,… предположим, нам нужно вычислить криволинейный интеграл по ломаной ![]() :
:
![]() , где
, где ![]() .
.
Да без проблем – представим его в виде суммы двух интегралов по отрезкам ![]() :
:
![]() – и вперёд с песнями.
– и вперёд с песнями.
И на всякий пожарный формула для кривой, заданной уравнением ![]() в полярных координатах:
в полярных координатах:
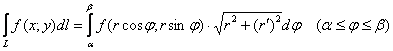
Кроме того, у криволинейного интеграла 1-го рода существуют физические приложения, в частности, с помощью него можно вычислить массу плоской дуги ![]() , если
, если ![]() – функция её плотности.
– функция её плотности.
Впрочем, криволинейные интегралы 1-го рода – это вообще нечастый гость в самостоятельных и контрольных работах (по крайне мере, у студентов-заочников), однако если вам этих примеров не достаточно, то загляните, например, во 2-й том К.А. Бохана. Там, к слову, вполне доступно разобрана и теория.
Мой же урок ориентирован на реальную практику, и по этой причине значительная его часть будет посвящена
криволинейным интегралам второго рода
«Реалити-шоу» точно такое же. Отличие будет в способе интегрирования. Если в интеграле ![]() мы объединяли бесконечно малые кусочки
мы объединяли бесконечно малые кусочки ![]() самой линии
самой линии ![]() , то сейчас интегрирование пойдёт по проекциям
, то сейчас интегрирование пойдёт по проекциям ![]() этих кусочков на ось абсцисс:
этих кусочков на ось абсцисс:
![]() ,
,
либо по их проекциям ![]() на ось ординат:
на ось ординат:
![]() ,
,
Следует заметить, что это два разных интеграла.и в общем случае ![]() .
.
Но в большинстве задач приходится иметь дело с так называемой общей формой криволинейного интеграла от двух функций:
![]()
С практической точки зрения будут важнЫ те же свойства линейности и аддитивности, а также тот факт, что:
криволинейный интеграл 2-го рода зависит от направления интегрирования, причём:
![]()
И в самом деле – здесь же интегрирование осуществляется не по длинам ![]() (которые беспрекословно положительны), а по их безразмерным проекциям, которые могут быть и отрицательными.
(которые беспрекословно положительны), а по их безразмерным проекциям, которые могут быть и отрицательными.
С чисто формальной точки зрения криволинейный интеграл 2-го рода «опознаётся» по наличию в подынтегральном выражении дифференциалов ![]() (намного реже – какого-то одного), и алгоритм его решения гораздо бесхитростнее, нежели «разборки» со «старшим братом»:
(намного реже – какого-то одного), и алгоритм его решения гораздо бесхитростнее, нежели «разборки» со «старшим братом»:
Пример 4
Вычислить криволинейный интеграл ![]() , где
, где ![]() – отрезок прямой от точки
– отрезок прямой от точки ![]() до точки
до точки ![]() . Выполнить чертёж.
. Выполнить чертёж.
Решение: на первом шаге нам нужно найти уравнение прямой, которая содержит отрезок ![]() . Составим его по двум точкам:
. Составим его по двум точкам:
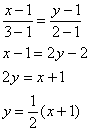
Несмотря на то, что линия интегрирования весьма простА, по условию требуется выполнить чертёж:
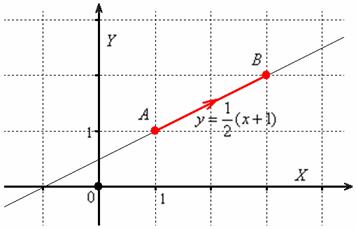
Обязательно указываем направление интегрирования! – здесь оно имеет принципиальное значение. Также обратите внимание на область определения подынтегральных функций – в данном примере ![]() , и поэтому линия интегрирования не должна пересекать координатные оси! Иногда авторы задачников и методичек недоглядывают за этим моментом, в результате чего получается невразумительное решение, где ответ, например, может оказаться бесконечным. Нет, конечно, мы вправе рассмотреть и несобственный криволинейный интеграл, но обычно задумка совсем не такая.
, и поэтому линия интегрирования не должна пересекать координатные оси! Иногда авторы задачников и методичек недоглядывают за этим моментом, в результате чего получается невразумительное решение, где ответ, например, может оказаться бесконечным. Нет, конечно, мы вправе рассмотреть и несобственный криволинейный интеграл, но обычно задумка совсем не такая.
Криволинейный интеграл 2-го рода тоже сводится к определённому интегралу с «избавлением» либо от всех «игреков», либо от всех «иксов».
Способ первый, традиционный, где осуществляется переход к интегрированию по переменной ![]() . Пределы интегрирования, как нетрудно догадаться, соответствуют «иксовым» координатам точек
. Пределы интегрирования, как нетрудно догадаться, соответствуют «иксовым» координатам точек ![]() , при этом не имеет значения, какой из них больше, а какой меньше; НО, принципиально важен порядок – интегрировать нужно строго по заданному направлению: от 1 до 3.
, при этом не имеет значения, какой из них больше, а какой меньше; НО, принципиально важен порядок – интегрировать нужно строго по заданному направлению: от 1 до 3.
Берём уравнение линии ![]() и находим дифференциал:
и находим дифференциал:
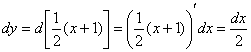
Подставим ![]() и
и ![]() в подынтегральное выражение – всё настолько прозрачно, что я даже формулу записывать не буду:
в подынтегральное выражение – всё настолько прозрачно, что я даже формулу записывать не буду:
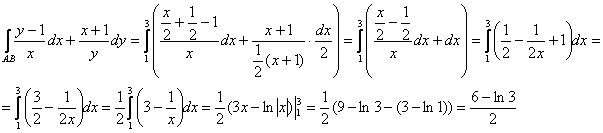
Ответ: ![]()
Если проинтегрировать наоборот – от точки ![]() до точки
до точки ![]() , то получится то же самое, только с другим знаком:
, то получится то же самое, только с другим знаком: 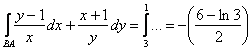 – в силу известного свойства определённого интеграла.
– в силу известного свойства определённого интеграла.
Способ второй состоит в переходе к интегрированию по переменной ![]() . Для этого из уравнения
. Для этого из уравнения ![]() выразим обратную функцию:
выразим обратную функцию:
![]()
и найдём дифференциал ![]() .
.
Перейдём к определённому интегралу от 1 до 2 («игрековые» координаты точек ![]() и
и ![]() ), подставив при этом в подынтегральное выражение
), подставив при этом в подынтегральное выражение ![]() и
и ![]() :
:
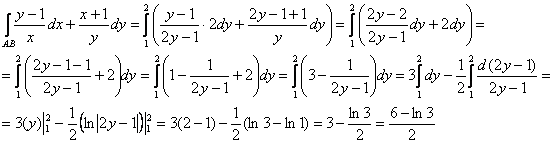
Второй способ оказался технически труднее, но, разумеется, бывает и наоборот. Поэтому перед решением всегда полезно «прикинуть» оба пути. И да – проверка же, не ленИтесь!
Но тут есть исключение: если фрагмент или весь путь интегрирования параллелен координатной оси, то способ остаётся только один! Ибо проекция этого участка на другую ось равна нулю.
Ответ: ![]()
Для самостоятельного решения я всегда стараюсь подбирать наиболее интересные задачи, которые мои студенты всегда выполняют с большим энтузиазмом иначе ни хрена не сдадут:);-)
Пример 5
Вычислить криволинейный интеграл ![]() от точки
от точки ![]() до точки
до точки ![]() вдоль ломаной, состоящей из отрезков прямых
вдоль ломаной, состоящей из отрезков прямых ![]() . Выполнить чертёж.
. Выполнить чертёж.
Краткое решение и ответ в конце урока.
У многих читателей наверняка назрел вопрос: в чём смысл такого интегрирования? У криволинейных интегралов 2-го рода есть каноничный физический смысл (и не только), с которым мы непременно познакомимся на следующем уроке (Интегрирование по замкнутому контуру и формула Грина). Всё будет – и примеры, и пояснения, и ссылки. А пока нарабатываем технические навыки.
Пример 6
Вычислить криволинейный интеграл ![]() , где
, где ![]() – дуга кривой
– дуга кривой ![]() от точки
от точки ![]() до точки
до точки ![]() .
.
Решение: для удобства выполним чертёж, не забывая подметить, что линия интегрирования не может пересекать ось ординат (т.к. ![]() ), впрочем, она здесь заведомо не может – ибо логарифм:
), впрочем, она здесь заведомо не может – ибо логарифм:
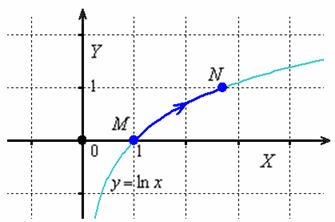
И сейчас я вас познакомлю с ещё одним приёмом решения. По причине той же аддитивности, интеграл можно разделить на две части:
![]() – и с каждым из них разделаться по отдельности:
– и с каждым из них разделаться по отдельности:
1) Вычислим ![]() . Так как
. Так как ![]() , то
, то ![]() (впрочем, дифференциал нам потребует только в пункте 2),
(впрочем, дифференциал нам потребует только в пункте 2), ![]() изменяется от 1 до
изменяется от 1 до ![]() :
:
![]()
Надеюсь, на данный момент все читатели понимают, как решать интеграл подведением функции под знак дифференциала. Результат, кстати, не помешает проверить интегрированием по «игрек»:
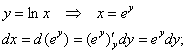
![]() изменяется от 0 до 1 (см. чертёж):
изменяется от 0 до 1 (см. чертёж):
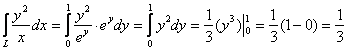 , что и требовалось проверить. Напоминаю, что второй путь можно смело выбирать и за основной.
, что и требовалось проверить. Напоминаю, что второй путь можно смело выбирать и за основной.
Со второй частью всё проще:
2) ![]()
Контроль по «игрек»: 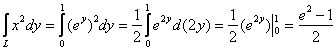
Осталось просуммировать полученные значения:
![]()
Ответ: ![]()
Разделение интеграла особенно удобно в тех случаях, когда подынтегральное выражение сильно «наворочено». Очередная «бомба» для самостоятельного решения:
Пример 7
Проверить, существует ли интеграл по данной кривой, и вычислить его, если это возможно
![]() – по дуге параболы
– по дуге параболы ![]() от точки
от точки ![]() до начала координат.
до начала координат.
Выполнить чертёж.
Вспоминаем, как интегрируются дроби. Краткое решение и ответ в конце урока.
И в заключение урока пара ласковых о параметрически заданной кривой:
Пример 8
Вычислить криволинейный интеграл ![]() по кривой
по кривой 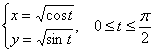
Решение: чертежа здесь, благо, чертить не требуется, да он и не нужен – условие таково, что снимай данные, да решай.
Как решать? Объясню буквально в 7 словах:)
– в подынтегральном выражении нужно всё выразить через параметр.
При этом во многих случаях, и в этом в частности, «начинку» удобно обработать отдельно. Сначала разбираемся с дифференциалами:
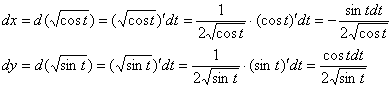
Теперь без спешки и ВНИМАТЕЛЬНО подставляем их вместе с прародителями ![]() в подынтегральное выражение, после чего аккуратно проводим упрощения:
в подынтегральное выражение, после чего аккуратно проводим упрощения:

И что приятно, тут не нужно думать над пределами изменения параметра:
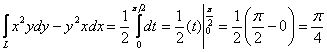
Ответ: ![]()
Самостоятельно:
Пример 9
Вычислить криволинейный интеграл ![]() по верхней половине эллипса
по верхней половине эллипса ![]() . Интегрировать против часовой стрелки.
. Интегрировать против часовой стрелки.
Статья о площади и объёме для параметрически заданной линии в помощь (Пример 2). Краткое решение и ответ совсем рядом.
Во второй части урока мы рассмотрим интереснейший случай интегрирования по замкнутому контуру, а также физический смысл криволинейного интеграла 2-го рода.
Жду вас с нетерпением!
Решения и ответы:
Пример 2. Решение: проекцией цилиндра ![]() на плоскость
на плоскость ![]() является «одноимённая» окружность единичного радиуса:
является «одноимённая» окружность единичного радиуса:
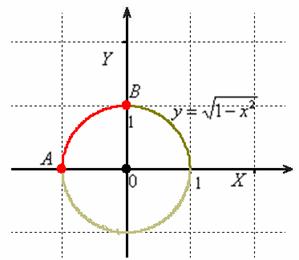
По условию, ![]() , следовательно:
, следовательно: ![]() , то есть в рассматриваемой области поверхность
, то есть в рассматриваемой области поверхность ![]() расположена ниже плоскости
расположена ниже плоскости ![]() . Площадь искомого фрагмента цилиндрической поверхности вычислим с помощью криволинейного интеграла 1-го рода по дуге
. Площадь искомого фрагмента цилиндрической поверхности вычислим с помощью криволинейного интеграла 1-го рода по дуге ![]() , при этом к интегралу следует добавить знак «минус» (по причине указанного выше обстоятельства):
, при этом к интегралу следует добавить знак «минус» (по причине указанного выше обстоятельства):
![]()
Интегрирование проведём по переменной ![]() от точки
от точки ![]() до точки
до точки ![]() . Так как
. Так как ![]() , то используем формулу
, то используем формулу 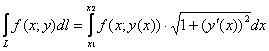 .
.
Примечание: можно интегрировать в обратном направлении (от 0 до –1), но тогда к интегралу следует добавить дополнительный минус.
Верхняя полуокружность задаётся функцией ![]() . Найдём производную и упростим корень:
. Найдём производную и упростим корень:
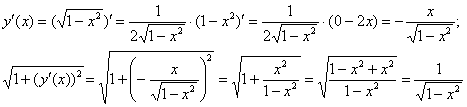
Таким образом:
![]()
Ответ: ![]()
Пример 5. Решение: выполним чертёж:
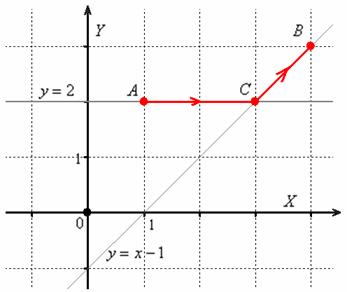
Интеграл по ломаной ![]() вычислим как сумму интегралов по её звеньям:
вычислим как сумму интегралов по её звеньям:
![]()
1) На отрезке ![]() :
: ![]() изменяется от 1 до 3:
изменяется от 1 до 3:
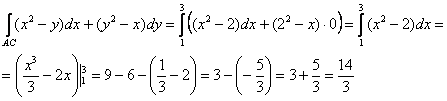
Примечание: т. к. ![]() параллелен оси абсцисс, то 2-й способ применить нельзя!
параллелен оси абсцисс, то 2-й способ применить нельзя!
2) На отрезке ![]() :
: ![]() изменяется от 3 до 4:
изменяется от 3 до 4:
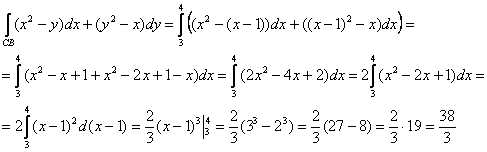
Ответ: ![]()
Пример 7. Решение: линия интегрирования спрямляема, непрерывна и не пересекает прямые ![]() , значит, данный криволинейный интеграл существует. Выполним чертёж:
, значит, данный криволинейный интеграл существует. Выполним чертёж:
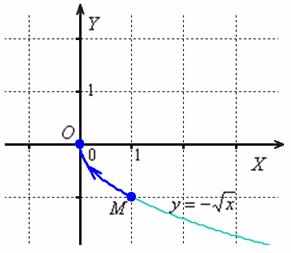
Представим интеграл в виде:
![]()
1) Вычислим ![]() .
.
![]() ,
, ![]() изменяется от 1 до 0:
изменяется от 1 до 0:

2) Вычислим ![]() .
.
![]() ,
, ![]() изменяется от –1 до 0:
изменяется от –1 до 0:
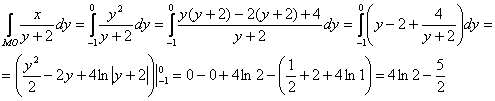
Таким образом:
![]()
Ответ: интеграл по данной кривой существует и равен ![]()
Пример 9. Решение: запишем параметрические уравнения эллипса:
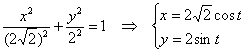
Найдём дифференциалы:
![]()
Выполним подстановку и упростим подынтегральное выражение:
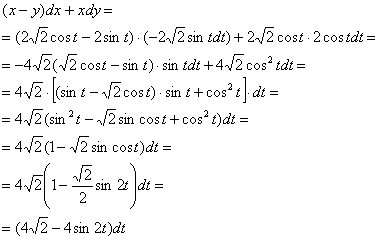
Предложенной дуге и направлению интегрирования соответствует изменение параметра от 0 до ![]() :
:
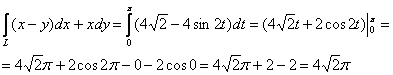
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright