mathprofi.ru

  Карта сайта

Эффективные методы решения
определённых и несобственных интегралов


Данная статья содержит дополнительные материалы по методам решения определённых и несобственных интегралов и предназначена для тех, кто хочет научиться их решать эффективнее. Предполагается, что читатель владеет средними или высокими навыками интегрирования, и для «чайников» я только что проставил ссылки на базовые уроки.

Если вам интересно что-то конкретное, оглавление:

И мы продолжаем.


Метод решения определённого интеграла от чётной функции
по симметричному относительно нуля отрезку

Рассмотрим определенный интеграл вида 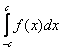. Легко заметить, что отрезок интегрирования  симметричен относительно нуля.

Если функция  подынтегральная  является чётной, то интеграл 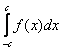 можно вычислить по половине отрезка, а результат – удвоить: .

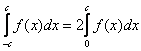Многие догадались, почему так, тем не менее, рассмотрим конкретный пример с чертежом:

Пример 1

Вычислить определенный интеграл.
О чётности функции много говорилось в справочном материале о графиках и функциях, повторим один раз: функция является чётной, если для неё выполняется равенство . Как проверить функцию на чётность? Нужно вместо «икс» подставить .

В данном случае , и мы проводим подстановку:
, значит, данная функция является чётной.

Согласно правилу, на симметричном относительно нуля отрезке  наш интеграл от чётной функции можно вычислить следующим образом:

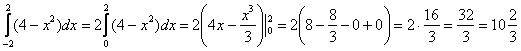
А сейчас геометрическая интерпретация. Да, продолжаем мучить несчастную параболу….

Любая чётная функция, в частности , симметрична относительно оси :
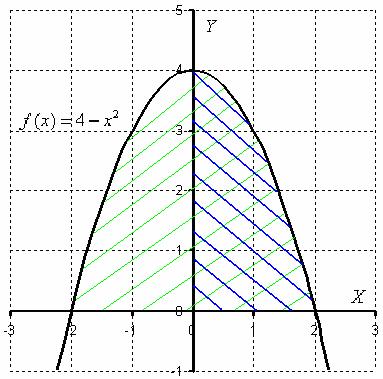
Определенный интеграл от четной функции по симметричному отрезку интегрирования

Определенный интеграл равен площади фигуры, которая заштрихована зеленым цветом. Но, в силу чётности подынтегральной функции, а значит, симметричности её графика относительно оси , достаточно вычислить площадь фигуры, заштрихованной синим цветом, а результат – удвоить. Одинаковые же половинки!
Именно поэтому справедливо действие .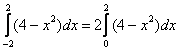

Аналогичная история происходит с любой чётной функцией  по симметричному относительно нуля отрезку:

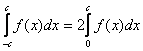
Некоторые скажут: «Да зачем это всё нужно, можно ведь и так вычислить определённый интеграл». Можно. Давайте вычислим:

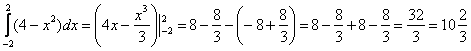
Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. Кстати, ненулевой процент студентов допустит ошибку в знаках. Гораздо проще и приятнее подставить ноль. Замечу, что это еще был простой демонстрационный пример, на практике всё бывает хуже.

Кроме того, рассматриваемый приём часто применяется при вычислении двойных интегралов, тройных интегралов, где вычислений и так хватает.

Короткий разминочный пример для самостоятельного решения:

Пример 2

Вычислить определенный интеграл.

Полное решение и ответ в конце урока.

Обратите внимание, что когда вам предложено просто вычислить определенный интеграл, то чертеж выполнять не нужно! Иллюстрация к Примеру 1 дана только для того, чтобы было понятно правило. Как раз данному моменту посвящена следующая простая задачка:

Пример 3

1) Вычислить определенный интеграл .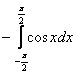
2) Вычислить площадь плоской фигуры, ограниченной линиями  и осью  на интервале .

Это две разные задачи! Об этом уже говорилось в статье Как вычислить площадь плоской фигуры? Сначала разберёмся с первым пунктом:

1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому:

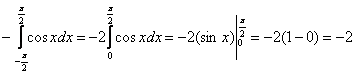
Определенный интеграл получился отрицательным и так бывает!

2) Теперь найдём площадь плоской фигуры. Вот здесь без чертежа обойтись трудно:
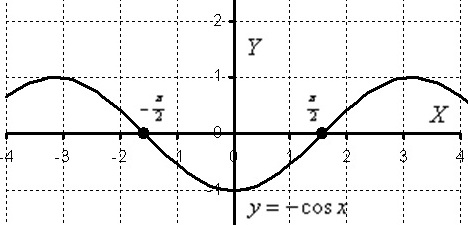
Различие определенного интеграла и задачи нахождения площади

Если у вас возникло затруднение с этим косинусом, пожалуйста, обратитесь к статье Геометрические преобразования графиков.

На отрезке  график функции расположен ниже оси , поэтому:

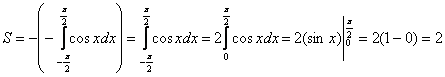
Площадь не может быть отрицательной, именно поэтому в формуле вычисления площади добавляют минус (также см. Пример 3 урока Определенный интеграл. Как вычислить площадь фигуры).

Заметьте, что чётность косинуса никто не отменял, поэтому мы опять споловинили отрезок и удвоили интеграл.


Вычисление площади круга с помощью определенного интеграла.
Тригонометрическая подстановка

Это очень важная задача, поскольку будет рассмотрен типовой интеграл и приём решения, который неоднократно встретится в будущем.

Но сначала небольшое напоминание по уравнению окружности. Уравнение вида  задаёт окружность с центром в точке  радиуса . В частности, уравнение  задаёт окружность радиуса  с центром в начале координат.

Пример 4

Вычислить площадь круга, ограниченного окружностью, заданной уравнением .

Изобразим на чертеже окружность с центром в начале координат радиуса :
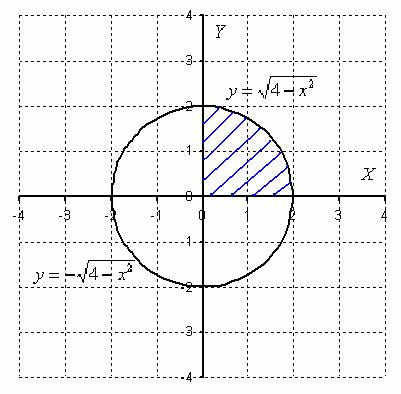
Как вычислить площадь круга с помощью определенного интеграла

Сначала вычислим площадь круга с помощью известной школьной формулы. Если радиус круга , то его площадь равна:

Для того чтобы вычислить площадь круга с помощью определенного интеграла, нужно из уравнения окружности  выразить «игрек» в явном виде:
.

Верхняя полуокружность задается функцией .
Нижняя полуокружность задается функцией .

Особые параноики, как я, могут подставить несколько точек окружности в эти функции и убедиться в справедливости вышеизложенных утверждений.

Как вычислить площадь круга? В данном примере круг симметричен относительно начала координат, поэтому достаточно вычислить площадь сектора в 1-й четверти (заштрихован синим цветом), затем результат умножить на 4.

Таким образом:

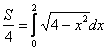
Такой же, только неопределенный интеграл рассматривался в Примере 6 урока Сложные интегралы, он решался длительным и трудоёмким методом сведения интеграла к самому себе. Можно пойти тем же путём, но для определенного интеграла существует удобный и эффективный метод тригонометрической замены.

Проведём замену: .

Почему именно такая замена, скоро станет понятно, а пока найдём дифференциал:

Выясним, во что превратится корень, распишу очень подробно:

Если в ходе решения вы не сможете догадаться применить формулу наподобие  , то, увы, схлопочете от преподавателя «приходите в следующий раз».

После преобразования корня отчетливо видно, почему проведена замена , особое внимание обращаю на коэффициент при синусе – двойке, этот коэффициент нужно подбирать таким образом, чтобы при возведении в квадрат всё хорошо вынеслось за скобки и из-под корня.

Осталось вычислить новые пределы интегрирования.
Если , то .

Новый нижний предел интегрирования: .
Новый верхний предел интегрирования: .

Таким образом:

Площадь сектора нужно умножить на 4, следовательно, площадь всей окружности:

Вероятно, у некоторых возник вопрос, зачем вообще мучиться с интегралом, если есть короткая школьная формула ?  А фишка состоит в том, что возможность очень точно вычислить площадь круга появилась только с развитием математического анализа (хотя уже в древности площадь круга рассчитывали с приличной точностью).

Разобранный пример можно решить в общем виде, то есть найти площадь круга, ограниченного окружностью произвольного радиуса: . В результате получится как раз формула !

Следует отметить, что к решению данной задачи можно было применить и другой подход – вычислить площадь верхнего полукруга с помощью интеграла , а затем удвоить результат. Но, в силу чётности подынтегральной функции, решение элементарно сводится к оптимальной версии:

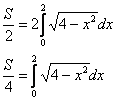
Ещё раз подчёркиваю важность проведенной тригонометрической замены, она встретится на практике не раз и не два. Поэтому для закрепления материала чуть более сложное задание для самостоятельного решения:

Пример 5

Вычислить определенный интеграл.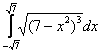

По условию требуется вычислить определенный интеграл, поэтому чертеж выполнять не нужно. Хорошо подумайте над коэффициентом в замене . Если возникнут трудности после замены, вернитесь к уроку Интегралы от тригонометрических функций. Будьте внимательны! Полное решение и ответ в конце урока.


Метод решения  определённого интеграла от нечётной функции
по симметричному относительно нуля отрезку

Вам понравится.

Рассмотрим тот же определенный интеграл с симметричным относительно нуля отрезком интегрирования: .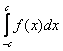
Если подынтегральная функция  является нечётной, то .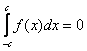

Почему такой интеграл равен нулю? 

Пример 6

Вычислить определенный интеграл

Выполним чертеж:
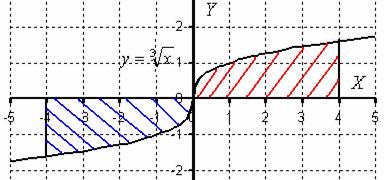
Определенный интеграл от нечетной функции по симметричному относительно нуля отрезку интегрирования

Вот заодно и график функции , который ещё нигде у меня не встречался, он представляет собой перевёрнутую кубическую параболу.

Проверим нашу функцию на чётность / нечётность, подставляем :
, значит, данная функция является нечётной и её график симметричен относительно начала координат. Из симметрии графика следует равенство площадей, которые заштрихованы красным и синим цветом.

При вычислении определенного интеграла  площадь, которая заштрихована синим цветом, формально является отрицательной. А площадь, которая заштрихована красным цветом – положительной. Поскольку площади равны и формально противоположны по знаку, то они «взаимоуничтожаются», следовательно, .

И еще раз подчеркиваю разницу между заданиями:

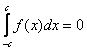1) Определённый интеграл (сам по себе) отрицательным быть может! Формально это площадь со знаком «минус». Поэтому , так как в силу нечётности функции , интегралы и площади «взаимно уничтожатся», что проиллюстрировано выше.

2) Задача на нахождение площади – это совершенно другая задача. Так, если бы нам было предложено найти площадь фигуры в данном примере, то её следовало бы вычислить следующим образом: .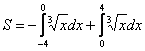

Еще несколько коротких примеров на тему данного правила:

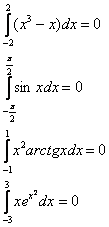
И аналогично для любой нечетной функции и симметричного относительно нуля отрезка.

Применять ли данный метод на практике? На самом деле вопрос не такой простой. Когда вам предложен сложный пример с большим количеством вычислений, то можно и даже уместно указать, что такой интеграл равен нулю, сославшись на нечетность функции и симметричность отрезка интегрирования относительно нуля. Как говорится, знание – сила, незнание – рабочая сила.

Но когда вам предложен короткий пример, то преподаватель вполне обоснованно может заставить прорешать его подробно: взять интеграл и подставить пределы интегрирования по формуле Ньютона-Лейбница. Например, вам предложено вычислить тот же определенный интеграл . Если вы сразу запишите, что  и поясните словами, почему получается ноль, то это будет не очень хорошо. Намного лучше «прикинуться простачком» и провести полное решение:

А то, что интеграл равен нулю, вы будете знать заранее ;-) И это знание 100%-но позволит избежать ошибки.


Метод решения несобственного интеграла с бесконечным нижним пределом

Второй раздел статьи предназначен для тех, кто хорошо разобрался с уроком Несобственные интегралы. Примеры решения, или, по крайне мере, понял бОльшую его часть. Начнём с несобственного интеграла первого рода с бесконечным нижним пределом: .

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Чем отличается данный интеграл от «обычного» несобственного интеграла с бесконечным верхним пределом? По технике решения практически ничем. Так же нужно найти первообразную, так же нужно использовать предел при вычислении интеграла. Отличие состоит в том, что здесь нужно устремить нижний предел интегрирования к «минус» бесконечности: .

Из вышесказанного следует очевидная формула для вычисления такого несобственного интеграла:

В данном примере, подынтегральная функция непрерывна на  и:
, то есть несобственный интеграл расходится.

Вот тут, главное, быть аккуратным в знаках, и не забывать, что . Нужно внимательно разобраться, что куда стремится.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.


Метод решения несобственного интеграла
с бесконечными пределами интегрирования

Очень интересный случай. Это тоже несобственный интеграл первого рода, где оба предела интегрирования бесконечны:

Как его решить? Данный интеграл можно представить в виде суммы двух несобственных интегралов:
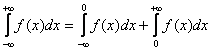(всё гениальное просто) и смотреть по ситуации:

Примечание: вместо нуля может быть любое число, но ноль обычно удобнее всего.

Пример 9

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция непрерывна на всей числовой прямой. Представляем интеграл в виде суммы двух интегралов:

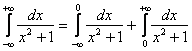
и разделываемся с ними по отдельности:

 

 

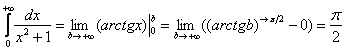
Таким образом:
, то есть несобственный интеграл существует и сходится.

Теперь обратим внимание на подынтегральную функцию. Она является чётной.

В несобственных интегралах с бесконечными пределами (а значит, симметричным интервалом интегрирования) чётностью пользоваться МОЖНО. Аналогично определённому интегралу, промежуток выгодно споловинить, а результат – удвоить:

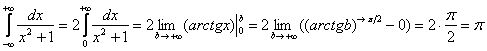
Почему такое возможно? График подынтегральной чётной функции  симметричен относительно оси . Следовательно, если половина площади конечна (интеграл сходится) – то симметричная половина площади тоже конечна. Если половина площади бесконечна (интеграл расходится), следовательно, симметричная половина тоже будет расходиться. И не забываем о третьем случае: если половины не существует, то второй и всего интеграла – тоже. Например:
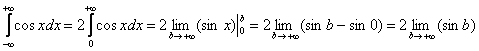 – данного предела не существует, а значит, не существует и несобственного интеграла .

Переходим ещё к более любопытному случаю:

Пример 10

Исследовать несобственный интеграл на сходимость.

Обратите внимание на задание – здесь в условии уже не констатируется факт существования интеграла.

Подынтегральная функция непрерывна на всей числовой прямой, и мы в академичном стиле распиливаем пациента на две части:

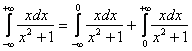
Решаем первый:

и второй:

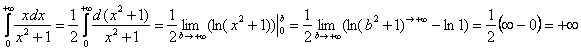
И, несмотря на то, что оба интеграла по отдельности расходятся – итогового интеграла в общем случае не существует, ибо сумма  не определена. Почему? Потому что переменная «а» может стремиться к «минус» бесконечности, например, БЫСТРЕЕ, чем переменная «бэ» к «плюс» бесконечности (или наоборот).

Но существует особый частный случай – когда обе переменные стремятся к бесконечностям одинаково. Это выражается пределом:

 и называется сходимостью интеграла по Коши. Само же значение предела называют главным значением несобственного интеграла.

И поскольку условие требовало от нас исследования, то здесь будет грамотным следующий ответ: в общем случае несобственного интеграла  не существует, однако имеет место сходимость по Коши и главное значение интеграла равно нулю. Главное значение принято обозначать так: .

А сейчас очень важный момент: подынтегральная функция  является нечётной, и, как вы правильно догадываетесь, в несобственных интегралах с бесконечными пределами нечётностью пользоваться НЕ СЛЕДУЕТ!!!

В этом состоит отличие от определенного интеграла. Там можно смело записать, что , а здесь так поступать не следует. Почему? Потому что в ряде случаев, как, например, в рассмотренном примере, получится автоматическая ошибка , что не соответствует действительности.

Тонкость же состоит в том, что интегралы  от некоторых нечётных функций и в самом деле равны нулю! И как раз этой тонкости посвящен следующий пример для самостоятельного решения:

Пример 11

Вычислить несобственный интеграл или установить его расходимость.

Полное решение и ответ в конце урока.


Метод решения несобственного интеграла второго рода
с точками разрыва на обоих концах отрезка

Заключительные пункты настоящей статьи предназначены для читателей, которые хорошо разобрались с несобственными интегралами второго рода. Рассмотрим другие разновидности этих интегралов. Ничего сложного!

Многие выкладки предыдущего параграфа будут справедливы и сейчас.

Сразу конкретная задача:

Пример 12

Вычислить несобственный интеграл или установить его расходимость:

Подынтегральная функция терпит бесконечные разрывы в обоих концах отрезка интегрирования. Изобразим подынтегральную функцию  на чертеже:
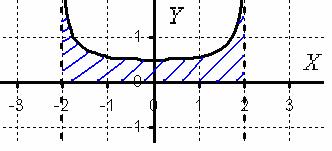
Несобственный интеграл второго рода с точками разрыва на обоих концах

Геометрически данный несобственный интеграл представляет собой площадь бесконечной криволинейной трапеции, которая не ограничена сверху.

Методика решения точно такая же, как и в предыдущем параграфе – разделяй и властвуй:

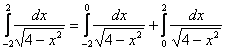
А уж интегралы правой части рассматривались во втором разделе урока Несобственные интегралы. Примеры решений.

Но, вместо этого замечаем, что подынтегральная функция является чётной. Чётность использовать МОЖНО. В этом легко убедиться и по чертежу. Таким образом, интеграл целесообразно споловинить, а результат удвоить. Решаем наиболее рациональным способом:

Подынтегральная функция терпит бесконечные разрывы в точках . Данная функция является чётной, а интервал интегрирования симметричен относительно нуля.

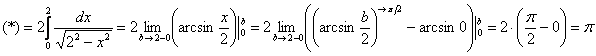
Ответ: , то есть несобственный интеграл сходится

Пример 13

Исследовать несобственный интеграл на сходимость ;)

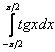
Это пример для самостоятельного решения. Всё, как и в предыдущем параграфе – нечетностью функции пользоваться НЕ НУЖНО. Аккуратно делим интеграл на две части и исследуем сходимость по типовому алгоритму. Полное решение и ответ близко.

Не редкость, когда подынтегральная функция не является чётной или нечётной, да и отрезок интегрирования не симметричен относительно нуля. Например, рассмотрим несобственный интеграл . Подынтегральная функция опять терпит бесконечные разрывы в обоих концах отрезка интегрирования. Алгоритм такой же, делим интеграл на два интеграла:

Интегралы правой части разобраны на уроке о несобственных интегралах. В качестве факультатива выясните, существует ли этот интеграл в общем случае, и если существует – то сходится или нет.


Метод решения несобственного интеграла
с точкой разрыва на отрезке интегрирования

Если честно, такой пример встречался в моей практике всего один раз (по крайне мере, вспомнил лишь один), поэтому я ограничусь только обзором.

Пример опять же будет в известной степени условным, первое, что в голову пришло. Рассмотрим несобственный интеграл 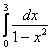. На концах отрезка интегрирования всё хорошо. Но подынтегральная функция терпит бесконечный разрыв прямо на отрезке в точке . Подынтегральная функция является четной, но это не имеет никакого значения, поскольку отрезок интегрирования не симметричен относительно нуля.

Метод уже состарился, как хмм… чешуя динозавра. Представим несобственный интеграл в виде суммы двух несобственных интегралов:

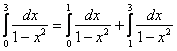
Интегралы правой части вам уже знакомы. А проговаривать алгоритм в третий раз не буду, смотрИте предыдущие два параграфа)

Желаю успехов!

Решения и ответы:

Пример 2. Решение:

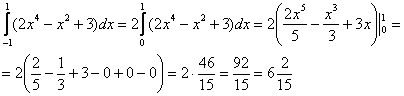
Пример 5. Решение:

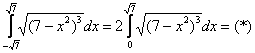
Проведем замену:

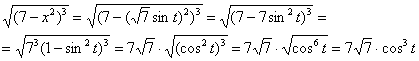
Новые пределы интегрирования:

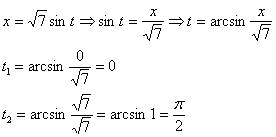
Пример 8. Решение:

Подынтегральная функция непрерывна на

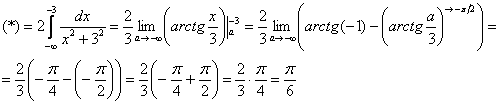
Пример 11. Решение: подынтегральная функция непрерывна на всей числовой прямой. Представим интеграл в виде суммы двух интегралов:

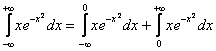
Вычислим первый интеграл:

Вычислим второй интеграл:

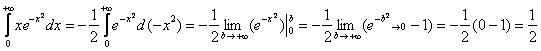
Таким образом:
– интеграл сходится и равен нулю.
Ответ:

Примечание 1: В частности, равно нулю и главное значение интеграла

Примечание 2: Будет серьезной оплошностью сразу записать, что , пользуясь нечетностью подынтегральной функции и симметричностью интервала интегрирования. Стандартный алгоритм обязателен!!!

Пример 13. Решение: 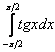подынтегральная функция терпит бесконечные разрывы в точках . Представим интеграл в виде суммы двух интегралов:

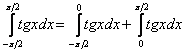
Вычислим первый интеграл:

Вычислим второй интеграл:

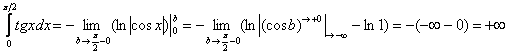
Таким образом, интеграла 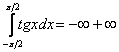 в общем случае не существует. Исследуем сходимость интеграла по Коши, используем чётность косинуса и свойство логарифмов:

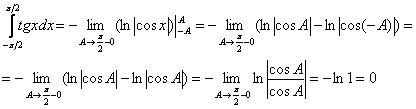
Ответ: интеграл сходится лишь по Коши, главное значение .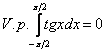

Автор: Емелин Александр


 Блог Емелина Александра

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?