

 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как исследовать несобственный интеграл на сходимость?
Приветствую опытных и не очень любителей несобственных интегралов, и на трёх ближайших уроках мы рассмотрим новый материал – признаки их сходимости.
Напоминаю основные типы несобственных интегралов:
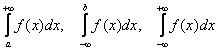 – несобственные интегралы 1-го рода;
– несобственные интегралы 1-го рода;
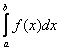 – несобственные интегралы 2-го рода, в которых функция
– несобственные интегралы 2-го рода, в которых функция ![]() терпит бесконечный разрыв в точке
терпит бесконечный разрыв в точке ![]() и / или
и / или ![]() или в промежуточных точках отрезка
или в промежуточных точках отрезка ![]() .
.
Предположим, что нам дан произвольный несобственный интеграл. В чём состоит сегодняшняя задача? Задача состоит в том, чтобы выяснить, СХОДИТСЯ ЛИ (в принципе) данный интеграл или нет.
Зачем это нужно? Ну, во-первых, иногда бывает полезно сразу выяснить этот вопрос. Во-вторых, рассмотрим, например, такие несобственные интегралы:
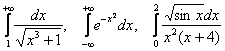
Здесь соответствующие неопределенные интегралы являются неберущимися, и поэтому решить данные примеры обычным способом невозможно. Но можно выяснить, сходятся ли эти интегралы или расходятся.
И, в-третьих, такие интегралы встречаются в практических работах, а значит, материал этой странички действительно нужен :) Более того, он тесно «перекликается» с исследованием числовых рядов, а значит, вы получите двойную выгоду. И я постараюсь изложить всю информацию в своём традиционном стиле – просто и доступно!
Вопрос третий: как определить, сходится ли несобственный интеграл или нет?
С помощью так называемых признаков сходимости / расходимости, к изучению которых мы незамедлительно приступаем.
Начнём с несобственных интегралов 1-го рода, и сразу признак:
если подынтегральная функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() и её предел
и её предел ![]() – существует и не равен нулю, то несобственный интеграл
– существует и не равен нулю, то несобственный интеграл 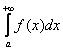 расходится.
расходится.
Это следует непосредственно из определения предела функции и особо очевидно в случае бесконечного предела ![]() , когда функция не ограничена сверху. Пожалуйста:
, когда функция не ограничена сверху. Пожалуйста: ![]() . Вспоминаем «школьный» график прямой пропорциональности
. Вспоминаем «школьный» график прямой пропорциональности ![]() . Что-то и сам проностальгировал:
. Что-то и сам проностальгировал:
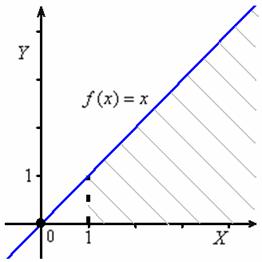
При ![]() этот график уходит вверх на плюс бесконечность, и совершенно понятно, что площадь под ним (серая штриховка) бесконечна:
этот график уходит вверх на плюс бесконечность, и совершенно понятно, что площадь под ним (серая штриховка) бесконечна: ![]() .
.
То же самое справедливо и для «страшных» интегралов наподобие 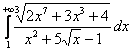 , которые на самом деле ничуть не страшнЫ. Во-первых, отмечаем непрерывность подынтегральной функции на промежутке интегрирования, и, во-вторых, выясняем порядок роста числителя и знаменателя – этим мы уже занимались, когда находили пределы функций. В числителе МЫСЛЕННО отбрасываем все младшие слагаемые под корнем:
, которые на самом деле ничуть не страшнЫ. Во-первых, отмечаем непрерывность подынтегральной функции на промежутке интегрирования, и, во-вторых, выясняем порядок роста числителя и знаменателя – этим мы уже занимались, когда находили пределы функций. В числителе МЫСЛЕННО отбрасываем все младшие слагаемые под корнем: ![]() и константу-множитель:
и константу-множитель: ![]() , следовательно, старшая степень числителя равна
, следовательно, старшая степень числителя равна ![]() . …Возникли трудности со степенями? Срочно повторять школьные формулы! В знаменателе тоже отбрасываем все младшие слагаемые:
. …Возникли трудности со степенями? Срочно повторять школьные формулы! В знаменателе тоже отбрасываем все младшие слагаемые: ![]() , следовательно, старшая степень знаменателя равна 2.
, следовательно, старшая степень знаменателя равна 2.
Неравенство ![]() говорит нам о том, что числитель более высокого порядка роста, чем знаменатель, а значит,
говорит нам о том, что числитель более высокого порядка роста, чем знаменатель, а значит, ![]() . То есть, при
. То есть, при ![]() подынтегральная функция не ограничена сверху и площадь под графиком данной функции на промежутке
подынтегральная функция не ограничена сверху и площадь под графиком данной функции на промежутке ![]() – бесконечна:
– бесконечна: 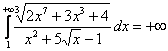 .
.
Актуализируем ещё пару важных фактов о порядке роста. Рассмотрим следующие несобственные интегралы от непрерывных на промежутке интегрирования функций:
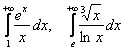
При ![]() показательная функция
показательная функция ![]() с основанием
с основанием ![]() более высокого порядка роста, чем любая степенная функция
более высокого порядка роста, чем любая степенная функция ![]() . Поэтому
. Поэтому ![]() и соответствующий несобственный интеграл
и соответствующий несобственный интеграл ![]() – расходится. Подчёркиваю, что в знаменателе может стоять «икс» хоть в сотой, хоть в тысячной степени, суммы степенных функций – результат от этого не изменится:
– расходится. Подчёркиваю, что в знаменателе может стоять «икс» хоть в сотой, хоть в тысячной степени, суммы степенных функций – результат от этого не изменится: ![]() . В справедливости предела
. В справедливости предела ![]() можно убедиться, 100 раз применив правило Лопиталя :)
можно убедиться, 100 раз применив правило Лопиталя :)
Второе. При ![]() степенная функция
степенная функция ![]() – более высокого порядка роста, чем натуральный логарифм, таким образом, функция
– более высокого порядка роста, чем натуральный логарифм, таким образом, функция ![]() (не ограничена сверху) и соответствующий несобственный интеграл расходится:
(не ограничена сверху) и соответствующий несобственный интеграл расходится: 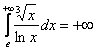 .
.
Возьмите на заметку эту информацию, она нам потребуется в будущем, в том числе самом близком.
Хорошо, если ![]() , то несобственный интеграл
, то несобственный интеграл 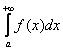 расходится. НО! Из того, что
расходится. НО! Из того, что ![]() , ещё не следует, что интеграл сходится. Он может, как сходиться, так и расходиться. В этом случае понятно лишь то, что подынтегральная функция ограничена на промежутке
, ещё не следует, что интеграл сходится. Он может, как сходиться, так и расходиться. В этом случае понятно лишь то, что подынтегральная функция ограничена на промежутке ![]() (и сверху и снизу).
(и сверху и снизу).
...На всякий случай приведу яркие примеры ограниченных функций, вдруг у кого недопонимание этого термина: экспонента ![]() – ограничена осью абсцисс снизу; синус:
– ограничена осью абсцисс снизу; синус: ![]() , арктангенс:
, арктангенс: ![]() – ограничены и сверху и снизу.
– ограничены и сверху и снизу.
! Откройте методичку по графикам (откроется на соседней вкладке), освежите воспоминания о графиках основных элементарных функций, и продолжаем. Справку не закрывать! – она будет здОрово помогать на сегодняшнем уроке.
В этой связи для исследования используют другие признаки, и наиболее распространенными из них являются так называемые признаки сравнения. Ключевая идея состоит в том, что СРАВНИТЬ «подопытный» интеграл с несобственным интегралом, сходимость или расходимость которого нам уже известна, и на этом основании сделать вывод о сходимости или расходимости «пациента».
Признак сравнения: пусть две неотрицательные функции ![]() непрерывны на промежутке
непрерывны на промежутке ![]() , и для всех
, и для всех ![]() этого промежутка справедливо неравенство
этого промежутка справедливо неравенство ![]() . Тогда из сходимости интеграла
. Тогда из сходимости интеграла 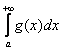 следует сходимость интеграла
следует сходимость интеграла 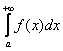 , а из расходимости
, а из расходимости 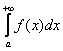 следует расходимость интеграла
следует расходимость интеграла 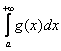 .
.
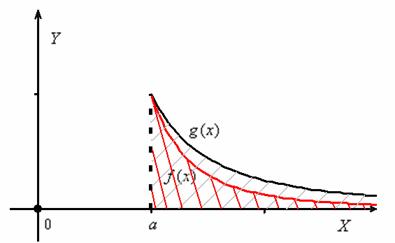
Таким образом, данный признак работает в двух различных ситуациях, геометрия которых очень и очень простА:
1) Пусть несобственный интеграл 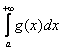 сходится. Тогда площадь, заштрихованная на чертеже серым цветом, будет конечна. В силу условия
сходится. Тогда площадь, заштрихованная на чертеже серым цветом, будет конечна. В силу условия ![]() график функции
график функции ![]() (красная линия) расположен не выше графика
(красная линия) расположен не выше графика ![]() и интегралу
и интегралу 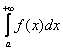 соответствует «красная» площадь, которая является ЧАСТЬЮ конечной «серой» площади. Следовательно, «красная» площадь тоже конечна, то есть несобственный интеграл
соответствует «красная» площадь, которая является ЧАСТЬЮ конечной «серой» площади. Следовательно, «красная» площадь тоже конечна, то есть несобственный интеграл 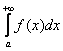 – сходится:
– сходится:
2) Ситуация вторая: пусть на том же промежутке ![]() интеграл
интеграл 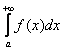 расходится. Это означает, что «красная» площадь бесконечна. А коль скоро она является частью «серой» площади, то интегралу
расходится. Это означает, что «красная» площадь бесконечна. А коль скоро она является частью «серой» площади, то интегралу 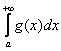 ничего не остаётся делать, как тоже расходиться.
ничего не остаётся делать, как тоже расходиться.
Такой же признак можно сформулировать для интегралов ![]() и, кроме того, для неположительных функций, удовлетворяющих условию
и, кроме того, для неположительных функций, удовлетворяющих условию ![]() , чертёж в последнем случае отобразится в нижнюю полуплоскость, симметрично относительно оси
, чертёж в последнем случае отобразится в нижнюю полуплоскость, симметрично относительно оси ![]() . Признаки сравнения для этих случаев сформулируйте и осознайте самостоятельно. На практике такие примеры встречаются, и они не должны поставить вас в тупик!
. Признаки сравнения для этих случаев сформулируйте и осознайте самостоятельно. На практике такие примеры встречаются, и они не должны поставить вас в тупик!
Но в первую очередь, конечно, традиционные примеры:
В начале вводного урока о несобственных интегралах мы установили сходимость интеграла ![]() . Теперь поставим задачу исследовать сходимость интеграла
. Теперь поставим задачу исследовать сходимость интеграла ![]() .
.
Подчёркиваю, что решать его не нужно (хотя делается это легко) – а нужно выяснить, сходится ли он (в принципе) или нет.
Прежде всего, обратим внимание, что функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() и её предел при
и её предел при ![]() равен нулю. Но, как отмечалось выше, это не делает погоды, а посему пробуем использовать признак сравнения. Сравнивать будем с интегралом
равен нулю. Но, как отмечалось выше, это не делает погоды, а посему пробуем использовать признак сравнения. Сравнивать будем с интегралом ![]() , сходимость которого уже установлена. Разбираемся:
, сходимость которого уже установлена. Разбираемся:
На промежутке ![]() функции
функции ![]() непрерывны? Да, непрерывны.
непрерывны? Да, непрерывны.
Неотрицательны? Да, более того, строго положительны: ![]() . Очень хорошо – условия признака выполнены, и поэтому можно приступать к анализу самих функций.
. Очень хорошо – условия признака выполнены, и поэтому можно приступать к анализу самих функций.
Для ВСЕХ ![]() из данного промежутка справедливо очевидное неравенство:
из данного промежутка справедливо очевидное неравенство:
![]()
а бОльшим знаменателям соответствуют мЕньшие дроби:
![]()
Вы согласны? В случае сомнений всегда можно взять несколько значений «икс» (проще всего целых) и расписать несколько неравенств подробно, чтобы убедиться в своей правоте или неправоте. В нашем случае:
если ![]() , то
, то ![]() ;
;
если ![]() , то
, то ![]() ;
;
если ![]() , то
, то ![]() ;
;
Если ![]() , то
, то ![]() ;
;
….
и теперь-то уж совершенно понятно, что для всех ![]() из промежутка
из промежутка ![]() неравенство
неравенство ![]() действительно справедливо.
действительно справедливо.
Таким образом, по признаку сравнения интеграл ![]() сходится (равен конечному числу) вместе с интегралом
сходится (равен конечному числу) вместе с интегралом ![]() . Кстати, на чертеже выше я «по партизански» изобразил именно графики функций
. Кстати, на чертеже выше я «по партизански» изобразил именно графики функций ![]() .
.
С помощью признака сравнения легко установить, что интеграл вида ![]() сходится при
сходится при ![]() и расходится, если
и расходится, если ![]() , а при
, а при ![]() он будет очевидно расходящимся.
он будет очевидно расходящимся.
Так, например, интегралы ![]() – сходятся, а
– сходятся, а ![]() – расходятся (в случаях непоняток со степенями повторяем формулы!).
– расходятся (в случаях непоняток со степенями повторяем формулы!).
Запишите данную информацию на листок!
Это семейство «эталонных» интегралов активно используется в практических заданиях, причём, опционально нижний предел интегрирования может быть и другим, например: 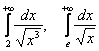 – зависит от того, какой интеграл предложен для исследования.
– зависит от того, какой интеграл предложен для исследования.
Пример 1
Исследовать сходимость интеграла ![]()
Решение: данный биномиальный интеграл является неберущимся, но есть возможность выяснить, сходится он или нет. Во-первых, отмечаем, что подынтегральная функция непрерывна на промежутке ![]() и предел
и предел ![]() – равен нулю. Таким образом, отделаться «малой кровью» у нас не получилось и решение продолжается.
– равен нулю. Таким образом, отделаться «малой кровью» у нас не получилось и решение продолжается.
По «общим очертаниям» предложенный интеграл напоминает сходящийся «эталон» ![]() . Начинаем проводить рассуждение. На промежутке
. Начинаем проводить рассуждение. На промежутке ![]() :
:
![]() (что совершенно очевидно). «Навешивание» корней сохраняет «статус-кво»:
(что совершенно очевидно). «Навешивание» корней сохраняет «статус-кво»:
![]() , а вот дела с дробями обстоят ровно наоборот – по той причине, что дробь с бОльшим знаменателем является мЕньшей:
, а вот дела с дробями обстоят ровно наоборот – по той причине, что дробь с бОльшим знаменателем является мЕньшей:
![]() , таким образом, по признаку сравнения исследуемый интеграл сходится вместе с интегралом
, таким образом, по признаку сравнения исследуемый интеграл сходится вместе с интегралом ![]() .
.
Ответ: сходится
И ничего лишнего – что спрашивали, то и отвечаем.
Подобных примеров можно придумать очень много: ![]() – сравниваем с соответствующими сходящимися интегралами
– сравниваем с соответствующими сходящимися интегралами ![]() .
.
Как вариант, знаменатель может быть «утяжелён» какой-нибудь возрастающей функцией – «иксом» в положительной степени, логарифмом, экспонентой: 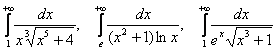 и т. д.
и т. д.
Все эти интегралы исследуются по той же схеме, единственное, здесь появляется дополнительная строчка в решении. Так, например, если в разобранном примере:
![]() , то, домножая левую часть на
, то, домножая левую часть на ![]() , мы только её увеличим, и поэтому неравенство:
, мы только её увеличим, и поэтому неравенство:
![]() будет выполнено подАвно.
будет выполнено подАвно.
Следовательно:
![]() , и по признаку сравнения, интеграл
, и по признаку сравнения, интеграл ![]() тоже сходится.
тоже сходится.
Разберём ещё одну классику жанра:
Пример 2
Исследовать сходимость интеграла ![]()
Решение: для удобства исследования перепишем его в виде ![]() . Очевидно, что подынтегральная функция непрерывна на промежутке интегрирования и предел
. Очевидно, что подынтегральная функция непрерывна на промежутке интегрирования и предел ![]() – равен нулю. Поэтому интеграл может как сходиться, так и расходиться.
– равен нулю. Поэтому интеграл может как сходиться, так и расходиться.
Сравним предложенный интеграл с интегралом![]() , сходимость которого выясняется в прямом смысле одной строкой:
, сходимость которого выясняется в прямом смысле одной строкой:
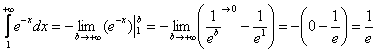
Для любого ![]() из промежутка
из промежутка ![]() справедливо неравенство:
справедливо неравенство:
![]() , и поскольку основание функции
, и поскольку основание функции ![]() , то:
, то:
![]()
а дробь с бОльшим знаменателем является мЕньшей:
![]() , таким образом, по признаку сравнения, интеграл
, таким образом, по признаку сравнения, интеграл ![]() сходится вместе с интегралом
сходится вместе с интегралом ![]() .
.
Ответ: сходится
И здесь интересно провести дополнительное исследование: в силу чётности подынтегральной функции, сходиться будет и интеграл по симметричному промежутку:![]() Кроме того, собственный или «обычный» определённый интеграл
Кроме того, собственный или «обычный» определённый интеграл ![]() , разумеется, тоже сходится, т. к. равен конечному числу.
, разумеется, тоже сходится, т. к. равен конечному числу.
Тогда, в силу свойства аддитивности, сходится и интеграл:
![]() . И парадоксально, но факт – данный интеграл рассчитан точно:
. И парадоксально, но факт – данный интеграл рассчитан точно: ![]() , невзирая на то, что соответствующий неопределенный интеграл не берётся. Да, так бывает! Это так называемый гауссов интеграл, который нам встретится в теории вероятностей, но желающие могут ознакомиться с его вычислением уже сейчас.
, невзирая на то, что соответствующий неопределенный интеграл не берётся. Да, так бывает! Это так называемый гауссов интеграл, который нам встретится в теории вероятностей, но желающие могут ознакомиться с его вычислением уже сейчас.
Другая вариация задания – это уменьшение числителя:
Пример 3
Исследовать сходимость интеграла ![]()
Решение: поскольку синус ограничен: ![]() , то
, то ![]() , и:
, и:
![]() , значит, по признаку сравнения исследуемый интеграл сходится вместе с интегралом
, значит, по признаку сравнения исследуемый интеграл сходится вместе с интегралом ![]() .
.
Ответ: сходится
И тут попутно возникает вопрос об интеграле ![]() , подынтегральная функция которого знакопеременна, т. е. постоянно меняет знак. Как быть в этом случае? Для таких интегралов существуют свои признаки, которые мы рассмотрим на уроке об условной и абсолютной сходимости интегралов. Ну а пока продолжаем.
, подынтегральная функция которого знакопеременна, т. е. постоянно меняет знак. Как быть в этом случае? Для таких интегралов существуют свои признаки, которые мы рассмотрим на уроке об условной и абсолютной сходимости интегралов. Ну а пока продолжаем.
Ситуация вторая: сравнение интеграла 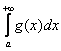 с заранее известным расходящимся интегралом
с заранее известным расходящимся интегралом 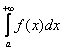 . Кратко напомню, что здесь на промежутке интегрирования должно выполняться то же неравенство
. Кратко напомню, что здесь на промежутке интегрирования должно выполняться то же неравенство ![]() . Как и в предыдущей ситуации, анализировать можно знаменатель или числитель:
. Как и в предыдущей ситуации, анализировать можно знаменатель или числитель:
Пример 4
Исследовать сходимость несобственных интегралов
а) ![]() , б)
, б) 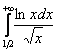
Скромно и со вкусом. И последнее «китайское» напоминание – в дальнейшем это будет подразумеваться по умолчанию: перед решением ВСЕГДА проверяем (мысленно или на черновике) непрерывность функции на промежутке интегрирования. Так, например, интеграл ![]() терпит бесконечный разрыв в точке
терпит бесконечный разрыв в точке ![]() , и для его исследования используются другие методы (о которых позже). Далее убеждаемся, что
, и для его исследования используются другие методы (о которых позже). Далее убеждаемся, что ![]() . А то может статься, промучаетесь с примером битый час, в то время как этот предел ненулевой, из чего сразу следует расходимость интеграла (см. примеры начала урока).
. А то может статься, промучаетесь с примером битый час, в то время как этот предел ненулевой, из чего сразу следует расходимость интеграла (см. примеры начала урока).
Решаем.
а) Множитель-константа не влияет на сходимость или расходимость, поэтому его можно сразу вынести за пределы интеграла:
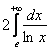
Для каждого ![]() промежутка
промежутка ![]() справедливо неравенство:
справедливо неравенство:
![]() (т. к. «икс» более высокого порядка роста, чем натуральный логарифм),
(т. к. «икс» более высокого порядка роста, чем натуральный логарифм),
а мЕньшим знаменателям соответствуют бОльшие дроби:
![]() , значит, по признаку сравнения исследуемый интеграл расходится вместе с «эталонным» интегралом
, значит, по признаку сравнения исследуемый интеграл расходится вместе с «эталонным» интегралом ![]() .
.
Вместо слова «ответ» я привык выделять вердикт жирным шрифтом, а при оформлении задания от руки подчёркивать его карандашом. Впрочем, кому как удобнее.
б) 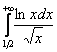 – а вот это вот более хитрый пример. Здесь напрашивается сравнение с расходящимся интегралом
– а вот это вот более хитрый пример. Здесь напрашивается сравнение с расходящимся интегралом ![]() , но не всё так просто. Во-первых, при
, но не всё так просто. Во-первых, при ![]() натуральный логарифм отрицателен (смотрим график!!). И, во-вторых, на участке
натуральный логарифм отрицателен (смотрим график!!). И, во-вторых, на участке ![]() этот логарифм меньше единицы, а значит, желаемое неравенство не является справедливым:
этот логарифм меньше единицы, а значит, желаемое неравенство не является справедливым: ![]() .
.
Что делать? Решение можно оформить двумя способами. Первый способ академичный. Согласно свойству аддитивности, делим интеграл на 3 части:
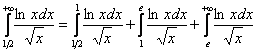
Первый и второй интегралы сходятся, т. к. являются определёнными интегралами. Для всех же значений ![]() справедливо неравенство:
справедливо неравенство:
![]() , значит, интеграл
, значит, интеграл 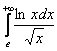 расходится вместе с интегралом
расходится вместе с интегралом ![]() ,
,
а значит, расходится и весь интеграл 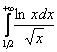 .
.
В укороченном способе оформления можно ограничиться такой фразой:
– при ![]() справедливо неравенство
справедливо неравенство ![]() – и тот же самый вывод.
– и тот же самый вывод.
Таким образом, сходимость или расходимость несобственного интеграла 1-го рода зависит от «поведения» его бесконечного «хвоста». Следует заметить, что все эти очевидные свойства строго доказываются в курсе математического анализа, но чтобы не перегружать вас информацией, я излагаю их в обзорно-популярном стиле.
Тренируемся самостоятельно:
Пример 5
Исследовать сходимость несобственных интегралов
а) ![]() , б)
, б) 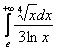 , в)
, в) 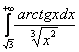 , г)
, г) 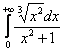 , д)
, д) ![]() , …пожалуй, достаточно.
, …пожалуй, достаточно.
Примерные образцы чистового оформления примеров в конце урока. И обязательно проверьте, успешно ли вы обошли все «подводные камни» ;)
Всегда ли работает рассмотренный признак сравнения? Нет, далеко не всегда, и сейчас мы рассмотрим примеры, ради которых и зашли некоторые более опытные читатели:
Пример 6
Исследовать сходимость несобственных интегралов
а) 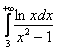 , б)
, б) ![]()
Решение:
а) По «общим очертаниям» интеграл напоминает сходящийся «эталон» ![]() , но как провести сравнение? Шаблон Примера 3 (интеграл
, но как провести сравнение? Шаблон Примера 3 (интеграл ![]() ) не годится, так как на промежутке
) не годится, так как на промежутке ![]() аналогичное неравенство является неверным:
аналогичное неравенство является неверным:
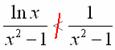
Но мы его всё равно организуем: при ![]() степенная функция
степенная функция ![]() , и в частности корень
, и в частности корень ![]() для любого
для любого ![]() – более высокого порядка роста, чем
– более высокого порядка роста, чем ![]() .
.
Следовательно:
![]()
Отмечу одну тонкость: если неравенство ![]() выполнено вообще для всех положительных «икс», то для более «мелких» корней, например
выполнено вообще для всех положительных «икс», то для более «мелких» корней, например ![]() , это утверждение неверно. Так, неравенство
, это утверждение неверно. Так, неравенство ![]() начинает выполняться лишь примерно с
начинает выполняться лишь примерно с ![]() , и поэтому при использовании таких корней нельзя применять формулировку «на всём промежутке интегрирования». Следует сказать уклончиво: «при
, и поэтому при использовании таких корней нельзя применять формулировку «на всём промежутке интегрирования». Следует сказать уклончиво: «при ![]() , по умолчанию подразумевая, что «начало» интеграла (где неравенство не выполнено) – тоже сходится.
, по умолчанию подразумевая, что «начало» интеграла (где неравенство не выполнено) – тоже сходится.
Однако возвращаемся к задаче. В силу установленного неравенства возникает вопрос сходимости интеграла 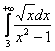 и тут возникает вторая загвоздка: поскольку
и тут возникает вторая загвоздка: поскольку ![]() , то нужное нам неравенство опять не выполняется:
, то нужное нам неравенство опять не выполняется:
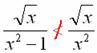
Что делать?
Предельный признак сравнения: пусть те же неотрицательные функции ![]() непрерывны на промежутке
непрерывны на промежутке ![]() и существует конечный предел их отношения
и существует конечный предел их отношения ![]() , отличный от нуля. Тогда интегралы
, отличный от нуля. Тогда интегралы 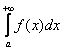 (1) и
(1) и 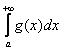 (2) сходятся или расходятся одновременно. Кроме того, при
(2) сходятся или расходятся одновременно. Кроме того, при ![]() из сходимости интеграла (2) следует сходимость интеграла (1), а при
из сходимости интеграла (2) следует сходимость интеграла (1), а при ![]() из расходимости того же интеграла (2) следует расходимость интеграла (1).
из расходимости того же интеграла (2) следует расходимость интеграла (1).
Но последняя часть признака применяется редко, гораздо чаще подбирают такой интеграл, чтобы получился конечный предел.
Итак, исследуем сходимость интеграла 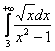 . Вопрос: с каким интегралом его нужно сравнить, чтобы в результате получился предел
. Вопрос: с каким интегралом его нужно сравнить, чтобы в результате получился предел![]() ?
?
Нечто подобное мы уже проделывали при вычислении пределов функций. Смотрим на знаменатель ![]() нашей функции и МЫСЛЕННО отбрасываем все младшие слагаемые:
нашей функции и МЫСЛЕННО отбрасываем все младшие слагаемые: ![]() – таким образом, старшая степень знаменателя равна 2. Поскольку в числителе находится только
– таким образом, старшая степень знаменателя равна 2. Поскольку в числителе находится только ![]() , то старшая степень числителя равна
, то старшая степень числителя равна ![]() . Теперь находим разность старших степеней:
. Теперь находим разность старших степеней: ![]() (строго такую, не наоборот!), и в результате приходим к выводу, что наш интеграл следует сравнить с интегралом
(строго такую, не наоборот!), и в результате приходим к выводу, что наш интеграл следует сравнить с интегралом 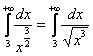 , который сходится.
, который сходится.
Составляем предел, избавляемся от четырёхэтажности дроби и получаем:
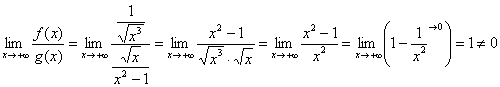 – конечное число, значит, по предельному признаку сравнения, интеграл
– конечное число, значит, по предельному признаку сравнения, интеграл 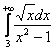 сходится вместе с интегралом
сходится вместе с интегралом ![]() .
.
И в силу установленного выше неравенства ![]() , исследуемый интеграл
, исследуемый интеграл 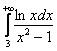 сходится вместе с интегралом
сходится вместе с интегралом 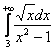 .
.
Таким образом, у нас получилась двухшаговое исследование, в котором мы использовали оба признака сравнения.
б) Интеграл ![]() . Проведём предварительный анализ: на промежутке
. Проведём предварительный анализ: на промежутке ![]() арктангенс ограничен:
арктангенс ограничен: ![]() , но эта информация помогает мало, т. к. на обоих этажах есть и другие одно- и многочлены с «иксами». И это типичная ситуация, в которой хорошо срабатывает предельный признак сравнения! Используем ту же методику: МЫСЛЕННО отбрасываем под корнем все младшие члены а также множитель-константу (двойку) при самой высокой степени:
, но эта информация помогает мало, т. к. на обоих этажах есть и другие одно- и многочлены с «иксами». И это типичная ситуация, в которой хорошо срабатывает предельный признак сравнения! Используем ту же методику: МЫСЛЕННО отбрасываем под корнем все младшие члены а также множитель-константу (двойку) при самой высокой степени: ![]() , значит, старшая степень знаменателя равна
, значит, старшая степень знаменателя равна ![]() . В числителе находится одинокий
. В числителе находится одинокий ![]() (ограниченный арк не принимаем во внимание), и поэтому старшая степень числителя равна 1.
(ограниченный арк не принимаем во внимание), и поэтому старшая степень числителя равна 1.
Из старшей степени знаменателя (именно так) вычитаем старшую степень числителя:
![]() , таким образом, наш интеграл следует сравнить с интегралом
, таким образом, наш интеграл следует сравнить с интегралом 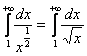 , который расходится. Возможно, у некоторых возник вопрос: а что делать, если разность степеней получилась отрицательной? Это означает, что числитель более высокого порядка роста, чем знаменатель, и интеграл расходится – вычисляем предел
, который расходится. Возможно, у некоторых возник вопрос: а что делать, если разность степеней получилась отрицательной? Это означает, что числитель более высокого порядка роста, чем знаменатель, и интеграл расходится – вычисляем предел ![]() , и готово.
, и готово.
Но в предельном признаке сравнения нас ожидает более занятный предел:
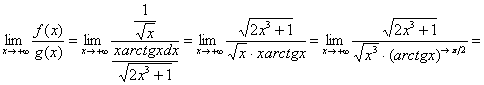
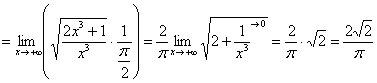 – конечное число, отличное от нуля, значит, исследуемый интеграл расходится вместе с интегралом
– конечное число, отличное от нуля, значит, исследуемый интеграл расходится вместе с интегралом ![]() .
.
Следует отметить, что при использовании предельного признака отношение функций можно составлять и наоборот, так, в только что разобранном примере можно составить предел 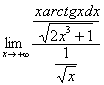 , получить
, получить ![]() и прийти к тому же содержательному выводу.
и прийти к тому же содержательному выводу.
Как быть, если нижний предел интегрирования равен нулю? Всё просто, по свойству аддитивности: 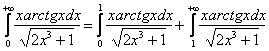 . Первый интеграл сходится (это обычный определённый интеграл, равный конечному числу), а для второго интеграла используем предельный признак сравнения (см. выше). Сумма сходящегося и расходящегося интеграла – есть расходящийся интеграл.
. Первый интеграл сходится (это обычный определённый интеграл, равный конечному числу), а для второго интеграла используем предельный признак сравнения (см. выше). Сумма сходящегося и расходящегося интеграла – есть расходящийся интеграл.
Такую же хитрость можно применить, если нижний предел отрицателен, но здесь важно проследить, чтобы промежуток интегрирования полностью вошёл в область определения подынтегральной функции. Так, интеграл 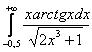 существует, но вот его собрат
существует, но вот его собрат ![]() – уже нет. И в легальном случае никаких проблем:
– уже нет. И в легальном случае никаких проблем:
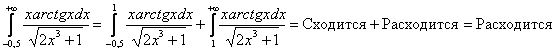 .
.
Интегралы для самостоятельного решения:
Пример 7
Исследовать сходимость несобственных интегралов:
а) 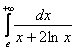 , б)
, б) ![]() , вот такой вот совсем не страшный красавец,
, вот такой вот совсем не страшный красавец,
и ещё один экземпляр, который прислал один из читателей сайта:
в) 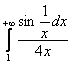 , сейчас мы узнАем, кто прогуливал матан в первом семестре :)
, сейчас мы узнАем, кто прогуливал матан в первом семестре :)
И хотел я тут продолжить про несобственные интегралы 2-го рода, но статья задалась недетская, а посему милости прошу во вторую часть, где нас ожидает самый настоящий «экшн»!
Решения и ответы:
Пример 5. Решение:
а) Сравним данный интеграл со сходящимся интегралом ![]() . На промежутке
. На промежутке ![]() :
:
![]() , значит, исследуемый интеграл тоже сходится.
, значит, исследуемый интеграл тоже сходится.
б) ![]() (т. к.
(т. к. ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() ), следовательно, исследуемый интеграл расходится.
), следовательно, исследуемый интеграл расходится.
в) На промежутке от ![]() до
до ![]() :
: ![]() , поэтому:
, поэтому:
![]() , значит, по признаку сравнения, исследуемый интеграл расходится вместе с интегралом
, значит, по признаку сравнения, исследуемый интеграл расходится вместе с интегралом ![]() .
.
г) На промежутке ![]() :
:
![]() , следовательно:
, следовательно:
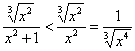 , таким образом, интеграл
, таким образом, интеграл 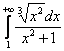 сходится вместе с интегралом
сходится вместе с интегралом ![]() .
.
И поскольку 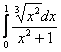 – сходится (обычный определённый интеграл), то сходится и весь исследуемый интеграл:
– сходится (обычный определённый интеграл), то сходится и весь исследуемый интеграл: 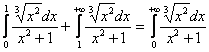 .
.
д) Способ первый. Использование признака сравнения. На промежутке ![]() :
:
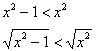
![]() , значит:
, значит:
![]() , то есть, исследуемый интеграл расходится вместе с интегралом
, то есть, исследуемый интеграл расходится вместе с интегралом ![]() .
.
Способ второй. Прямое вычисление. Перед нами табличный «длинный» логарифм:
![]() , таким образом, исследуемый интеграл расходится.
, таким образом, исследуемый интеграл расходится.
Пример 7. Решение:
а) Сравним предложенный интеграл с расходящимся интегралом ![]() . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
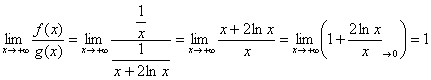 (т. к.
(т. к. ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() ). В результате получено конечное число, отличное от нуля, значит, исследуемый интеграл расходится вместе с интегралом
). В результате получено конечное число, отличное от нуля, значит, исследуемый интеграл расходится вместе с интегралом ![]() .
.
б) Поскольку косинус ограничен: ![]() , то
, то ![]() и:
и:
![]() (*)
(*)
Исследуем сходимость интеграла ![]() (множитель-константа не влияет на сходимость или расходимость, и поэтому его сразу выносим). Старшая степень знаменателя равна 3, старшая степень числителя равна
(множитель-константа не влияет на сходимость или расходимость, и поэтому его сразу выносим). Старшая степень знаменателя равна 3, старшая степень числителя равна ![]() , их разность:
, их разность:
![]() , поэтому сравнивать будем со сходящимся интегралом
, поэтому сравнивать будем со сходящимся интегралом ![]() . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
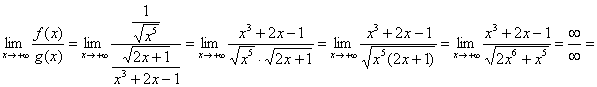
делим числитель и знаменатель на ![]() в старшей степени:
в старшей степени:
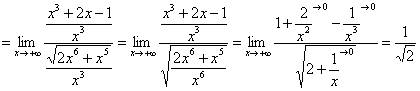 – получено конечное число, отличное от нуля, значит, интеграл
– получено конечное число, отличное от нуля, значит, интеграл ![]() сходится вместе с интегралом
сходится вместе с интегралом ![]() и, в силу неравенства (*) (по «обычному» признаку сравнения), исследуемый интеграл сходится вместе с интегралом
и, в силу неравенства (*) (по «обычному» признаку сравнения), исследуемый интеграл сходится вместе с интегралом ![]() .
.
в) Прежде всего, вычислим предел подынтегральной функции. Используем замечательную эквивалентность ![]() при
при ![]() , в данном случае
, в данном случае ![]() :
:
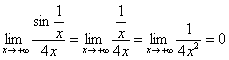 , таким образом, интеграл может, как сходиться, так и расходиться. И, анализируя решение этого предела, нетрудно понять, что наш интеграл нужно сравнить со сходящимся интегралом
, таким образом, интеграл может, как сходиться, так и расходиться. И, анализируя решение этого предела, нетрудно понять, что наш интеграл нужно сравнить со сходящимся интегралом ![]() . Используем предельный признак сравнения и ту же эквивалентность:
. Используем предельный признак сравнения и ту же эквивалентность:
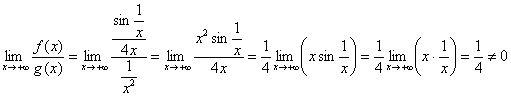 – конечное число, стало быть, интеграл
– конечное число, стало быть, интеграл 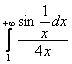 тоже сходится.
тоже сходится.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright