


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Приближенные вычисления с помощью рядов
После изучения основных понятий функциональных и степенных рядов, задачи разложения функций в ряды переходим к обширной группе приложений рассматриваемой темы. К основным заданиям, которые часто встречаются на практике, относятся следующие:
– приближённое вычисление значения функции с помощью ряда;
– приближённое вычисление определённого интеграла с помощью ряда;
– нахождение частного решения ДУ приближённо с помощью ряда.
На данном уроке мы рассмотрим первую, наиболее простую задачу, для решения которой потребуются самые элементарные знания о рядах, таблица разложений функций в степенные ряды и микрокалькулятор. Как вариант, пойдёт Эксель (если умеете управляться с его функциями). Вычислительные задачи требуют повышенной концентрации внимания, поэтому к изучению статьи рекомендую подойти в хорошей физической форме и со свежей головой:
Существует 2 типа рассматриваемой задачи, с которыми мы на самом деле уже сталкивались ранее, в частности при вычислении интеграла по формуле трапеций и методом Симпсона. Тип первый:
Пример 1
Используя разложение функции в ряд, вычислить число ![]() , ограничившись 5 членами разложения. Результат округлить до 0,001. Провести вычисления на калькуляторе и найти абсолютную погрешность вычислений.
, ограничившись 5 членами разложения. Результат округлить до 0,001. Провести вычисления на калькуляторе и найти абсолютную погрешность вычислений.
Решение: прежде всего, выбираем подходящее табличное разложение функции. Очевидно, что в нашем случае нужно взять следующий ряд:
![]() , который сходится при любом значении «икс».
, который сходится при любом значении «икс».
Кратко повторим, что такое сходимость функционального ряда: чем больше слагаемых мы рассмотрим, тем точнее функция-многочлен будет приближать функцию ![]() . Действительно, график параболы
. Действительно, график параболы ![]() совсем не напоминает экспоненту и график кубической функции
совсем не напоминает экспоненту и график кубической функции ![]() тоже далёк от идеала, но если взять 50-100 членов ряда, то картина в корне поменяется. И, наконец, график бесконечного многочлена
тоже далёк от идеала, но если взять 50-100 членов ряда, то картина в корне поменяется. И, наконец, график бесконечного многочлена ![]() совпадёт с графиком экспоненциальной функции
совпадёт с графиком экспоненциальной функции ![]() .
.
Примечание: в теории даже есть такой подход и определение: функция ![]() – это сумма функционального ряда
– это сумма функционального ряда ![]() .
.
В условии прямо сказано, что нужно просуммировать 5 первых членов ряда, причём, результат следует округлить до 0,001. И поэтому проблем здесь никаких:
![]()
Вычислим более точное значение с помощью микрокалькулятора:
![]()
Абсолютная погрешность вычислений:
![]() – ну что же, вполне и вполне неплохо. Но бывает лучше.
– ну что же, вполне и вполне неплохо. Но бывает лучше.
Ответ: ![]()
Теперь рассмотрим нескольку другую разновидность задания:
Пример 2
Используя разложение функции в ряд, вычислить ![]() приближённо с точностью до 0,001.
приближённо с точностью до 0,001.
! Примечание: иногда аргумент бывает выражен в градусах, в таких случаях его следует перевести в радианы.
Давайте вспомним смысл выражения «с точностью до 0,001». Оно обозначает, что наш ответ должен отличаться от истины не более чем на 0,001.
Решение: используя табличное разложение ![]() , запишем несколько членов соответствующего ряда, при этом округление лучше проводить с «запасом» – до 5-6 знаков после запятой:
, запишем несколько членов соответствующего ряда, при этом округление лучше проводить с «запасом» – до 5-6 знаков после запятой:
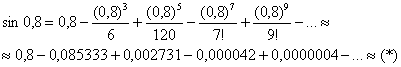
Сколько членов ряда следует просуммировать для достижения требуемой точности? Для сходящихся знакочередующихся рядов справедлив следующий критерий: члены следует суммировать до тех пор, пока они по модулю больше заданной точности. Первый же меньший вместе со всем «хвостом» подлежит утилизации. В данном примере таковым является 4-й член: ![]() , поэтому:
, поэтому:
![]() – с округлением финального результата до требуемой точности.
– с округлением финального результата до требуемой точности.
Ответ: ![]() с точностью до 0,001
с точностью до 0,001
Наверное, все понимают, почему она гарантирована: здесь к отрицательному 4-му члену ![]() прибавляется мЕньшее по модулю число
прибавляется мЕньшее по модулю число ![]() , затем из результата вычитается ещё более малое число
, затем из результата вычитается ещё более малое число ![]() – и так далее до бесконечности. Образно говоря, конструкция напоминает маятник с затухающими колебаниями, где
– и так далее до бесконечности. Образно говоря, конструкция напоминает маятник с затухающими колебаниями, где ![]() – самый большой размах в отрицательную сторону, «затмевающий» собой все остальные движения.
– самый большой размах в отрицательную сторону, «затмевающий» собой все остальные движения.
Очевидно, что для сходящихся положительных рядов (ближайший пример – Пример 1) рассмотренный критерий некорректен. Условно говоря, если 0,00034 < 0,001, то сумма «хвоста» может запросто превзойти 0,001 (т. к. ВСЕ члены ряда положительны). И к этому вопросу я ещё вернусь позже:
Пример 3
Вычислить ![]() с точностью до 0,001
с точностью до 0,001
Пример 4
Вычислить ![]() приближённо, используя первые два члена соответствующего разложения. Оценить абсолютную погрешность вычислений.
приближённо, используя первые два члена соответствующего разложения. Оценить абсолютную погрешность вычислений.
Это примеры для самостоятельного решения. Разумеется, выгодно сразу же найти ![]() чтобы эффективно контролировать ход решения.
чтобы эффективно контролировать ход решения.
И возникает вопрос: зачем заниматься такими нелепыми вещами, если есть калькуляторы, расчётные программы? Отчасти я дал ответ на уроке Приближенные вычисления с помощью дифференциала. Не так уж и давно калькулятор был большой редкостью, не говоря о такой роскоши, как клавиши с надписями ![]() и т. д. В гостевой книге сайта одна из посетительниц поделилась воспоминаниями, как все расчёты своего диплома проводила с помощью математических таблиц и логарифмической линейки. А такой инструментарий наряду с механическими счётами сегодня займут место разве что в музее истории математики.
и т. д. В гостевой книге сайта одна из посетительниц поделилась воспоминаниями, как все расчёты своего диплома проводила с помощью математических таблиц и логарифмической линейки. А такой инструментарий наряду с механическими счётами сегодня займут место разве что в музее истории математики.
Резюме таково – мы решаем устаревшую задачу. Насущный же практический смысл состоит в том, что её нужно решить =) Ну, может ещё по информатике будет полезно кому – приближенная сумма с наперёд заданной точностью элементарно алгоритмизируется циклом. Правда, какой-нибудь Паскаль довольно быстро сломается, поскольку факториал растёт семимильными шагами.
Кроме того, есть ещё одно очень важное и актуальное приложение, имеющее прикладное значение, но этот секрет будет раскрыт по ходу урока ;-) Выдвигайте гипотезы, если догадаетесь – респект.
Также не следует упускать из внимания область сходимости предлагаемых рядов, разложения синуса, косинуса и экспоненты – да, сходятся при любом «икс», но разобранные примеры не должны усыплять бдительность! Простейшая иллюстрация – арктангенс и его разложение ![]() . Если попытаться вычислить, скажем, значение
. Если попытаться вычислить, скажем, значение ![]() , то легко заметить неограниченный рост (по модулю) членов ряда, который не приведёт нас к какому бы то ни было конечному, и тем более приближённому значению. А всё потому, что
, то легко заметить неограниченный рост (по модулю) членов ряда, который не приведёт нас к какому бы то ни было конечному, и тем более приближённому значению. А всё потому, что ![]() не входит в область сходимости
не входит в область сходимости ![]() данного разложения.
данного разложения.
Разберём более трудные задания:
Пример 5
Вычислить ![]() с точностью до 0,01
с точностью до 0,01
Решение: щёлкаем по клавишам калькулятора: ![]() . И думаем, как выполнить приближённые вычисления с помощью ряда. В ситуациях с корнем дело сводится к биномиальному разложению
. И думаем, как выполнить приближённые вычисления с помощью ряда. В ситуациях с корнем дело сводится к биномиальному разложению ![]() с гарантированным интервалом сходимости
с гарантированным интервалом сходимости ![]() .
.
Пытаемся представить наш радикал в виде ![]() :
:
![]()
И всё бы было хорошо, но только значение ![]() не входит в область сходимости рассматриваемого биномиального ряда, то есть конструкция
не входит в область сходимости рассматриваемого биномиального ряда, то есть конструкция ![]() не годится для вычислений – произойдёт такой же несчастный случай, как с рассмотренным выше
не годится для вычислений – произойдёт такой же несчастный случай, как с рассмотренным выше ![]() .
.
Как быть? Ещё раз смотрим на значение ![]() и замечаем, что оно близко к «тройке». В самом деле:
и замечаем, что оно близко к «тройке». В самом деле: ![]() . Используя замечательного соседа, проводим следующее типовое преобразование: под корнем выделяем число 27, искусственно выносим его за скобки и далее выносим из-под корня:
. Используя замечательного соседа, проводим следующее типовое преобразование: под корнем выделяем число 27, искусственно выносим его за скобки и далее выносим из-под корня:
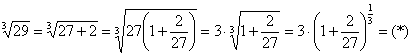
Вот теперь всё тип-топ: число ![]() принадлежит интервалу сходимости
принадлежит интервалу сходимости ![]() . Но в качестве «побочного эффекта» возникает необходимость поправить точность вычислений. Ведь когда мы подсчитаем члены разложения
. Но в качестве «побочного эффекта» возникает необходимость поправить точность вычислений. Ведь когда мы подсчитаем члены разложения 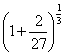 , то будем обязаны домножить каждое число на «тройку». И по этой причине изначально требуемую точность 0,01 нужно устрожить в три раза:
, то будем обязаны домножить каждое число на «тройку». И по этой причине изначально требуемую точность 0,01 нужно устрожить в три раза: ![]() .
.
Итак, используем ряд ![]() , в котором
, в котором ![]() . Не забываем проверить по таблице разложений, не подпадает ли наш пример под какой-нибудь частный случай биномиального разложения. Нет. А, значит, придётся работать ручками:
. Не забываем проверить по таблице разложений, не подпадает ли наш пример под какой-нибудь частный случай биномиального разложения. Нет. А, значит, придётся работать ручками:
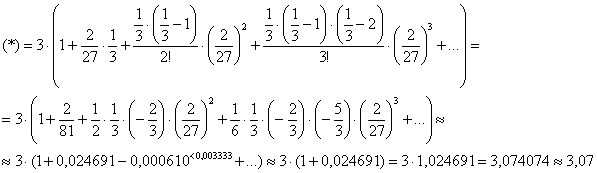
Тут для достижения необходимой точности (заметьте, что члены начали знакочередоваться!) хватило трёх слагаемых, и четвёртого монстра ![]() считать не было смысла. Но «про запас» всегда стараемся расписать побольше членов ряда. Если поленитесь и не хватит слагаемых – будете заново переписывать всё задание.
считать не было смысла. Но «про запас» всегда стараемся расписать побольше членов ряда. Если поленитесь и не хватит слагаемых – будете заново переписывать всё задание.
Ответ: ![]() с точностью до 0,01
с точностью до 0,01
Да, вычисления, конечно, не подарочные, но что поделать….
Более простая вариация на ту же тему для самостоятельного решения:
Пример 6
Вычислить ![]() , ограничившись первыми тремя членами ряда. Результат округлить до 3 знаков после запятой.
, ограничившись первыми тремя членами ряда. Результат округлить до 3 знаков после запятой.
Образец оформления задачи в конце урока. И не забываем вновь обратиться к вычислительной технике: ![]() .
.
Что студент с нетерпением ждёт изо дня в день? Логарифмы:
Пример 7
Вычислить ![]() с точностью до 0,001
с точностью до 0,001
Решение: сначала, как всегда, узнаем ответ: ![]() .
.
Очевидно, что здесь нужно использовать разложение ![]()
И это действительно возможно, т. к. значение ![]() входит в область сходимости
входит в область сходимости ![]() данного ряда.
данного ряда.
Считаем:
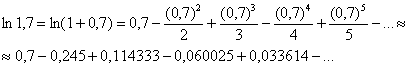
Стоп. Что-то здесь не так. Сойтись-то ряд сойдётся, но такими темпами вычисления могут затянуться до скончания века. И научный тык в неравенство ![]() подсказал, что этот конец наступит после счастливого номера
подсказал, что этот конец наступит после счастливого номера ![]() .
.
Таким образом, ряд ![]() сходится довольно медленно и пригоден для вычислений разве что
сходится довольно медленно и пригоден для вычислений разве что ![]() и других логарифмов, аргумент которых достаточно близок к единице.
и других логарифмов, аргумент которых достаточно близок к единице.
В целях значительного ускорения процесса несложно вывести следующее разложение:
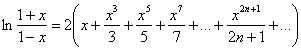 с областью сходимости
с областью сходимости ![]()
Приятная вещь состоит в том, что всякое положительное число ![]() (кроме единицы) можно представить в виде
(кроме единицы) можно представить в виде ![]() . Преобразуем аргумент логарифма в обыкновенную дробь:
. Преобразуем аргумент логарифма в обыкновенную дробь: ![]() и решим следующее уравнение:
и решим следующее уравнение:
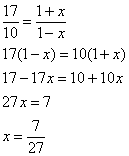
Проверка: 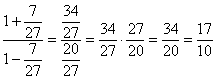
«Заряжаем»:
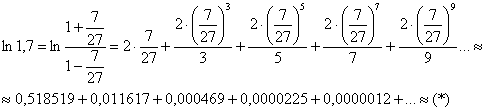
И теперь у нас обнаружилась другая проблемка – ряд-то, оказывается, положительный, и поэтому здесь нельзя указать ![]() и отбросить весь «хвост». Вдруг он в своей сумме окажется больше, чем 0,001? В этой связи используем более хитрый метод оценки. Сохранив «на всякий случай» подозрительно большой 3-й член, рассмотрим остаток ряда:
и отбросить весь «хвост». Вдруг он в своей сумме окажется больше, чем 0,001? В этой связи используем более хитрый метод оценки. Сохранив «на всякий случай» подозрительно большой 3-й член, рассмотрим остаток ряда:
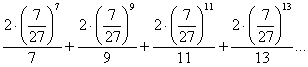
Числа 9, 11, 13, … в знаменателях меняем на 7 – тем самым только увеличивая члены, а значит, и всю сумму остатка:
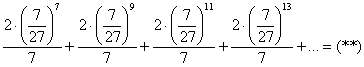
Далее выполняем обычные алгебраические преобразования и находим сумму бесконечно убывающей геометрической прогрессии по формуле ![]() :
:
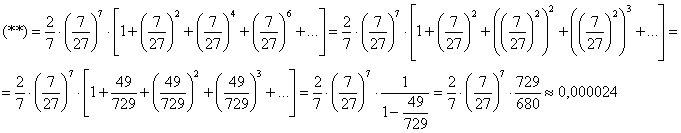
По-научному, это называется подбором мажорантного сходящегося ряда (в данном случае – геом. прогрессии), сумму которого легко отыскать (или которая известна). И план оказался не только выполнен, но и перевыполнен! Отбрасывая все члены ряда, начиная с 4-го, будет гарантирована точность 0,00002! Впрочем, по условию результат всё равно нужно округлить до трёх знаков после запятой:
![]()
Ответ: ![]() с точностью до 0,001
с точностью до 0,001
Ну и осталось с чувством голубого морального удовлетворения свериться с более точным значением ![]() .
.
…А может быть, было проще вычислить сумму 12 членов медленно сходящегося ряда? =) Впрочем, в следующем задании такой возможности уже не будет в принципе:
Пример 8
Вычислить ![]() с точностью до 0,001
с точностью до 0,001
– по той причине, что значение ![]() не входит в область сходимости ряда
не входит в область сходимости ряда ![]() .
.
Дерзайте!
Статья начиналась с приближённого вычисления числа «е», и закончим мы её другой знаменитой константой:
Приближённое вычисление числа 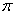 с помощью ряда
с помощью ряда
О «пи» исписаны километры бумаги и сказаны миллионы слов, поэтому я не буду загружать вас историей, теорией и гипотезами, если интересно (а это и на самом деле интересно), обратитесь, например, к Википедии. Данное число обладает бесконечным количеством знаков после запятой: ![]() , и теория рядов предоставляет один из эффективных способов нахождения этих цифр:
, и теория рядов предоставляет один из эффективных способов нахождения этих цифр:
Пример 9
Используя значение ![]() и разложение арктангенса в ряд Маклорена вычислить приближённо число
и разложение арктангенса в ряд Маклорена вычислить приближённо число ![]() , используя первые пять членов ряда. Оценить количество верных знаков.
, используя первые пять членов ряда. Оценить количество верных знаков.
Решение: запишем первые пять членов разложения в ряд арктангенса: 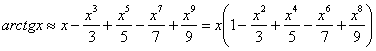
В данном случае ![]() :
:
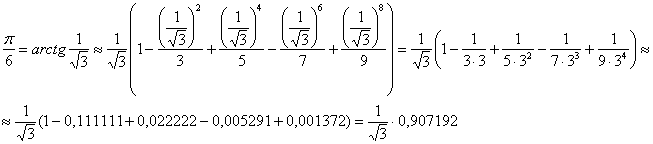
В результате ![]() , откуда легко выразить приближённое значение:
, откуда легко выразить приближённое значение:
![]()
Ответ: ![]() , данный способ даёт два верных знака после запятой.
, данный способ даёт два верных знака после запятой.
Очевидно, что чем больше членов ряда рассмотреть, тем точнее будет найдено число «пи». Кроме того, существуют значительно более быстро сходящиеся ряды, позволяющие малым количеством слагаемых получить очень высокую точность.
На сегодня найдены многие миллиарды верных цифр после запятой, в последовательности которых не обнаружено каких-либо закономерностей. Доходит до того, что всевозможные экстрасенсы и философы считают, что в данном числе зашифровано всё-всё-всё на белом свете.
А если откинуть мистику, то вычисление чисел «е», «пи» и других констант имеет важное прикладное значение, так, например, в астрономических или квантовых расчётах верный 100-й знак после запятой может играть существенную и даже принципиальную роль.
Да будут потёрты клавиши вашего калькулятора =)
Решения и ответы:
Пример 3. Решение: используем разложение ![]() .
.
В данном случае ![]() :
:
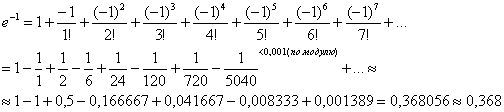
Ответ: ![]() с точностью до 0,001
с точностью до 0,001
Пример 4. Решение: используем разложение ![]() . Вычислим сумму двух первых членов ряда:
. Вычислим сумму двух первых членов ряда: ![]() . Так как ряд является знакочередующимся, то абсолютная погрешность не превзойдёт по модулю третьего члена:
. Так как ряд является знакочередующимся, то абсолютная погрешность не превзойдёт по модулю третьего члена: ![]()
Ответ: ![]() , абсолютная погрешность вычислений – не более чем
, абсолютная погрешность вычислений – не более чем ![]()
Пример 6. Решение: преобразуем радикал:
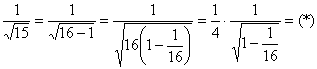
Используем частный случай биномиального разложения:
![]() , в данном случае
, в данном случае ![]() – принадлежит области сходимости ряда.
– принадлежит области сходимости ряда.
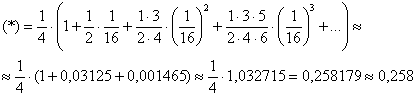
Ответ: ![]()
Пример 8. Решение: для самопроверки вычислим данное значение на калькуляторе: ![]() .
.
Используем разложение: ![]() .
.
Представим аргумент в виде обыкновенной дроби ![]() и найдём
и найдём ![]() :
:
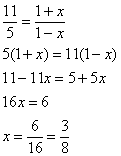
Таким образом:
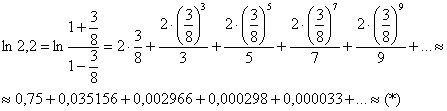
Предполагая, для достижения требуемой точности будет достаточно 3 членов, оценим остаток ряда:
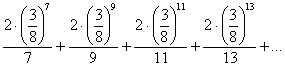
Числа 9, 11, 13… заменим на 7, тем самым только увеличив члены ряда. Выполним преобразования и найдём сумму бесконечно убывающей геометрической прогрессии ![]() :
:
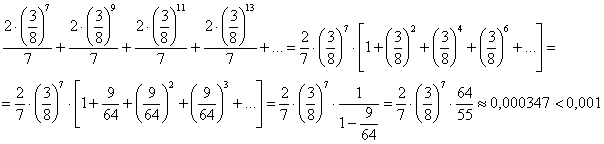
Таким образом, первые три члена ряда гарантируют требуемую точность:
![]()
Ответ: ![]() с точностью до 0,001
с точностью до 0,001
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright