


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Сложные производные. Логарифмическая производная.
Производная степенно-показательной функции
Продолжаем повышать свою технику дифференцирования. На данном уроке мы закрепим пройденный материал, рассмотрим более сложные производные, а также познакомимся с новыми приемами и хитростями нахождения производной, в частности, с логарифмической производной.
Тем читателям, у кого низкий уровень подготовки, следует обратиться к статье Как найти производную? Примеры решений, которая позволит поднять свои навыки практически с нуля. Далее необходимо внимательно изучить страницу Производная сложной функции, понять и прорешать все приведенные мной примеры. Данный урок логически третий по счету, и после его освоения Вы будете уверенно дифференцировать достаточно сложные функции. Нежелательно придерживаться позиции «Куда ещё? Да и так хватит!», поскольку все примеры и приёмы решения взяты из реальных контрольных работ и часто встречаются на практике.
Начнем с повторения. На уроке Производная сложной функции мы рассмотрели ряд примеров с подробными комментариями. В ходе изучения дифференциального исчисления и других разделов математического анализа – дифференцировать придется очень часто, и не всегда бывает удобно (да и не всегда нужно) расписывать примеры очень подробно. Поэтому мы потренируемся в устном нахождении производных. Самым подходящими «кандидатами» для этого являются производные простейших из сложных функций, например:
![]()
По правилу дифференцирования сложной функции ![]() :
:
![]()
При изучении других тем матана в будущем такая подробная запись чаще всего не требуется, предполагается, что студент умеет находить подобные производные на автопилоте автомате. Представим, что в 3 часа ночи раздался телефонный звонок, и приятный голос спросил: «Чему равна производная тангенса двух икс?». На это должен последовать почти мгновенный и вежливый ответ: ![]() .
.
Первый пример будет сразу предназначен для самостоятельного решения.
Пример 1
Найти следующие производные устно, в одно действие, например: ![]() . Для выполнения задания нужно использовать только таблицу производных элементарных функций (если она ещё не запомнилась). Если возникнут затруднения, рекомендую перечитать урок Производная сложной функции.
. Для выполнения задания нужно использовать только таблицу производных элементарных функций (если она ещё не запомнилась). Если возникнут затруднения, рекомендую перечитать урок Производная сложной функции.
![]() ,
, ![]() ,
, 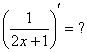 ,
,
![]() ,
, 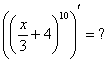 ,
,  ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
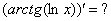 ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]()
Ответы в конце урока
Сложные производные
После предварительной артподготовки будут менее страшны примеры, с 3-4-5 вложениями функций. Возможно, следующие два примера покажутся некоторым сложными, но если их понять (кто-то и помучается), то почти всё остальное в дифференциальном исчислении будет казаться детской шуткой.
Пример 2
Найти производную функции ![]()
Как уже отмечалось, при нахождении производной сложной функции, прежде всего, необходимо правильно РАЗОБРАТЬСЯ во вложениях. В тех случаях, когда есть сомнения, напоминаю полезный приём: берем подопытное значение «икс», например, ![]() и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
1) Сначала нам нужно вычислить выражение ![]() , значит, сумма
, значит, сумма ![]() – самое глубокое вложение.
– самое глубокое вложение.
2) Затем необходимо вычислить логарифм: ![]()
3) Далее косинус: ![]()
4) Потом косинус возвести в куб: ![]()
5) На пятом шагу разность: ![]()
6) И, наконец, самая внешняя функция – это квадратный корень: ![]()
Формула дифференцирования сложной функции ![]() применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:
применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:
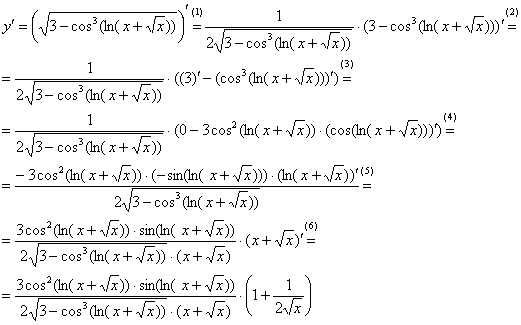
Вроде без ошибок….
(1) Берём производную от квадратного корня.
(2) Берём производную от разности, используя правило ![]()
(3) Производная тройки равна нулю. Во втором слагаемом берём производную от степени (куба).
(4) Берём производную от косинуса.
(5) Берём производную от логарифма.
(6) И, наконец, берём производную от самого глубокого вложения ![]() .
.
Может показаться слишком трудно, но это еще не самый зверский пример. Возьмите, например, сборник Кузнецова и вы оцЕните всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Следующий пример для самостоятельного решения.
Пример 3
Найти производную функции ![]()
Подсказка: сначала применяем свойство линейности (первые два правила) и правило дифференцирования произведения
Полное решение и ответ в конце урока.
Настало время перейти к чему-нибудь более компактному и симпатичному.
Не редка ситуация, когда в примере дано произведение не двух, а трёх функций. Как найти производную от произведения трёх множителей?
Пример 4
Найти производную функции ![]()
Сначала смотрим, а нельзя ли произведение трёх функций превратить в произведение двух функций? Так, если бы у нас было два многочлена, то можно было бы раскрыть скобки и получить один. Но здесь все функции разные: степень, экспонента и логарифм.
В таких случаях нужно последовательно применить правило дифференцирования произведения ![]() два раза
два раза
Фокус состоит в том, что за «у» мы обозначим произведение двух функций: ![]() , а за «вэ» – логарифм:
, а за «вэ» – логарифм: ![]() . Почему так можно сделать? А разве
. Почему так можно сделать? А разве ![]() – это не произведение двух множителей и правило не работает?! Ничего сложного нет:
– это не произведение двух множителей и правило не работает?! Ничего сложного нет:
![]()
Теперь осталось второй раз применить правило ![]() к скобке
к скобке ![]() :
:
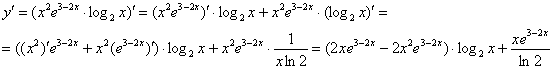
Можно еще поизвращаться и вынести что-нибудь за скобки, но в данном случае ответ лучше оставить именно в таком виде – легче будет проверять.
Готово.
Рассмотренный пример можно решить вторым способом, обозначив за «у» степень, а за «вэ» – произведение экспоненты и логарифма::
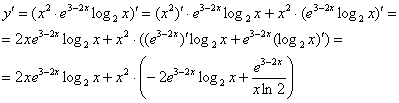
Оба способа решения абсолютно равноценны.
Пример 5
Найти производную функции ![]()
Это пример для самостоятельного решения, в образце он решён первым способом.
Рассмотрим аналогичные примеры с дробями.
Пример 6
Найти производную функции ![]()
Здесь можно пойти несколькими путями:
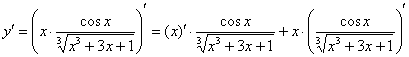
или так:
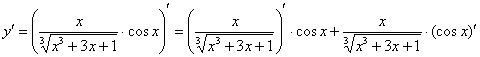
Но решение запишется более компактно, если в первую очередь использовать правило дифференцирования частного 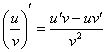 , приняв за
, приняв за ![]() весь числитель:
весь числитель:
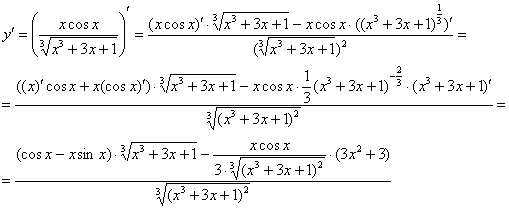
В принципе, пример решён, и если его оставить в таком виде, то это не будет ошибкой. Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить? Приведём выражение числителя к общему знаменателю и избавимся от трёхэтажности дроби:
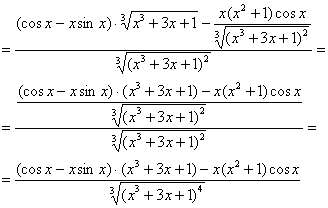
Минус дополнительных упрощений состоит в том, что есть риск допустить ошибку уже не при нахождении производной, а при банальных «школьных» преобразованиях. С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную.
Более простой пример для самостоятельного решения:
Пример 7
Найти производную функции ![]()
Продолжаем осваивать приёмы нахождения производной, и сейчас мы рассмотрим типовой случай, когда для дифференцирования предложен «страшный» логарифм
Пример 8
Найти производную функции ![]()
Тут можно пойти длинным путём, используя правило дифференцирования сложной функции:
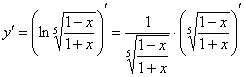
Но первый же шаг сразу повергает в уныние – предстоит взять неприятную производную от дробной степени ![]() , а потом ещё и от дроби
, а потом ещё и от дроби ![]() .
.
Поэтому перед тем как брать производную от «навороченного» логарифма, его предварительно упрощают, используя известные школьные свойства:
![]()
![]()
![]()
! Если под рукой есть тетрадь с практикой, перепишите эти формулы прямо туда. Если тетради нет, перерисуйте их на листочек, поскольку оставшиеся примеры урока буду вращаться вокруг этих формул.
Итак, преобразуем логарифм:
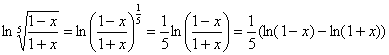
Строго говоря, в общем случае эти преобразования неравносильны (справедливы не для всех «икс»), но при нахождении производных сиё формально допустимо.
Берём производную, в несложных случаях логарифм можно упростить прямо под штрихом и даже за один шаг:
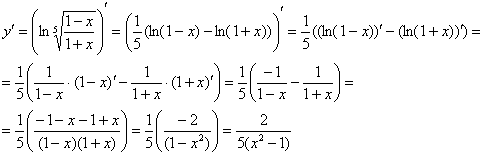
Как видите, предварительное преобразование логарифма значительно облегчило решение. Таким образом, когда для дифференцирования предложена подобная конструкция, то её целесообразно «развалить».
А сейчас пара несложных примеров для самостоятельного решения:
Пример 9
Найти производную функции ![]()
Пример 10
Найти производную функции ![]()
Все преобразования и ответы в конце урока.
Логарифмическая производная (логарифмическое дифференцирование)
Если производная от логарифмов – это такая сладкая музыка, то возникает вопрос, а нельзя ли в некоторых случаях организовать логарифм искусственно? Можно! И даже нужно.
Пример 11
Найти производную функции 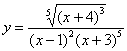
Похожие примеры мы недавно рассмотрели. Что делать? Можно последовательно применить правило дифференцирования частного, а потом правило дифференцирования произведения. Недостаток способа состоит в том, что получится огромная трёхэтажная дробь, с которой совсем не хочется иметь дела.
Но в теории и практике есть такая замечательная вещь, как логарифмическая производная или (синоним) логарифмическое дифференцирование. Логарифмы можно организовать искусственно, «навесив» их на обе части:
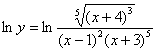
По-научному это называется логарифмированием.
Примечание: т. к. функция может принимать отрицательные значения, то, вообще говоря, нужно использовать модули: 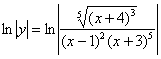 , которые исчезнут в результате дифференцирования. Однако допустимо и текущее оформление, где по умолчанию принимаются во внимание комплексные значения. Но если со всей строгостью, то и в том и в другом случае следует сделать оговорку, что
, которые исчезнут в результате дифференцирования. Однако допустимо и текущее оформление, где по умолчанию принимаются во внимание комплексные значения. Но если со всей строгостью, то и в том и в другом случае следует сделать оговорку, что ![]() .
.
Теперь нужно максимально «развалить» логарифм правой части (формулы перед глазами?). Я распишу этот процесс очень подробно:
![]()
![]()
![]()
![]()
Собственно приступаем к дифференцированию.
Заключаем под штрих обе части:
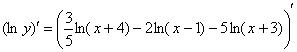
Производная правой части достаточно простая, её я комментировать не буду, поскольку если вы читаете этот текст, то должны уверенно с ней справиться.
Как быть с левой частью?
В левой части у нас сложная функция. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?».
Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ. Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции ![]() :
:
![]()
В левой части как по мановению волшебной палочки у нас «нарисовалась» производная ![]() . Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:
. Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:
![]()
А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие: 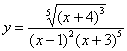
Окончательный ответ:
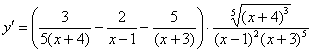
Пример 12
Найти производную функции ![]()
Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока.
С помощью логарифмической производной можно было решить любой из примеров № 4-7, другое дело, что там функции проще, и, может быть, использование логарифмической производной не слишком-то и оправдано.
Производная степенно-показательной функции
Данную функцию мы еще не рассматривали. Степенно-показательная функция – это функция, у которой и основание и показатель степени зависят от «икс». Классический пример, который вам приведут в любом учебнике и на любой лекции:
![]()
Как найти производную степенно-показательной функции? Нужно использовать только что рассмотренный приём – логарифмическое дифференцирование.
Навешиваем логарифмы на обе части:
![]()
и сносим «икс» на землю за пределы лографима:
![]()
В результате в правой части у нас получилось произведение двух функций, которое будет дифференцироваться по стандартной формуле ![]() .
.
Находим производную, для этого заключаем обе части под штрихи:
![]()
Дальнейшие действия несложны:
![]()
Окончательно: ![]()
Если какое-то преобразование не совсем понятно, пожалуйста, внимательно перечитайте объяснения Примера № 11.
В практических заданиях степенно-показательная функция всегда будет сложнее, чем рассмотренный лекционный пример.
Пример 13
Найти производную функции ![]()
Используем логарифмическую производную.
![]()
![]()
В правой части у нас константа и произведение двух множителей – «икса» и «логарифма логарифма икс» (под логарифм вложен ещё один логарифм). При дифференцировании константу, как мы помним, лучше сразу вынести за знак производной, чтобы она не мешалась под ногами; и, конечно, применяем знакомое правило ![]() :
:
![]()
![]()
![]()
Как видите, алгоритм логарифмического дифференцирования не содержит в себе каких-то особых хитростей или уловок, и нахождение производной степенно-показательной функции обычно не связано с «мучениями».
Заключительные два примера предназначены для самостоятельного решения.
Пример 14
Найти производную функции ![]()
Пример 15
Найти производную функции ![]()
Образцы решения и оформления совсем близко.
Не такое и сложное это дифференциальное исчисление.
Желаю успехов!
Решения и ответы:
Пример 1:
![]() ,
, ![]() ,
, 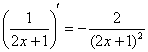 ,
,
![]() ,
, 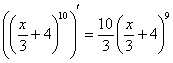 ,
, 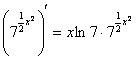 ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]()
Пример 3:

Пример 5:
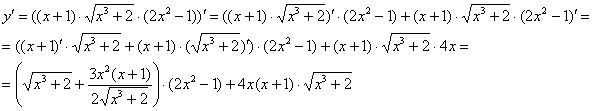
Примечание: перед дифференцированием можно было раскрыть скобки ![]() и использовать правило
и использовать правило ![]() один раз.
один раз.
Пример 7:
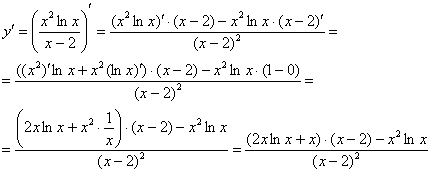
Пример 9: используем свойства логарифмов и правило дифференцирования сложной функции:
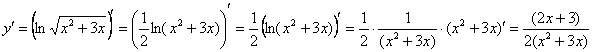
Пример 10: используем свойства логарифмов:
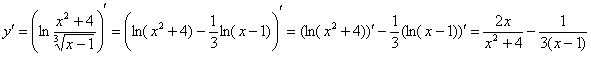
Пример 12: используем логарифмическую производную. Преобразуем функцию:
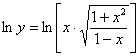
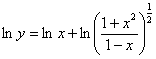
![]()
![]()
Находим производную:
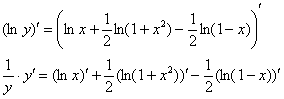
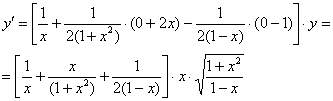
Пример 14: используем логарифмическую производную:
![]()
![]()
![]()
![]()
![]()
Пример 15: используем логарифмическую производную:
![]()
![]()
![]()
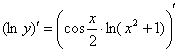
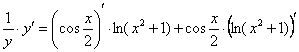
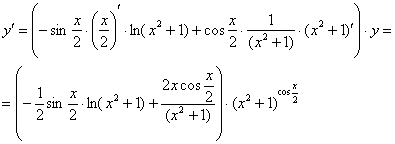
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright