


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как вычислить длину дуги кривой?
Помимо нахождения площади и объёма тела вращения, вездесущий определённый интеграл позволяет рассчитать и другие показатели, в частности длину дуги кривой.
И в данной статье мы узнаем, как вычислить данную величину, если линия задана функцией ![]() , либо параметрически
, либо параметрически ![]() , или же уравнением
, или же уравнением ![]() в полярной системе координат. Для каждого случая будут разобраны практические примеры с подробными комментариями о типичных особенностях решения этой задачи. Более того, по ходу изложения материала вас ждёт специальное предложение, которое должно понравиться ;-)
в полярной системе координат. Для каждого случая будут разобраны практические примеры с подробными комментариями о типичных особенностях решения этой задачи. Более того, по ходу изложения материала вас ждёт специальное предложение, которое должно понравиться ;-)
Пусть некоторая функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , и её график на данном промежутке представляет собой кривую или, что то же самое, дугу кривой
, и её график на данном промежутке представляет собой кривую или, что то же самое, дугу кривой ![]() :
:
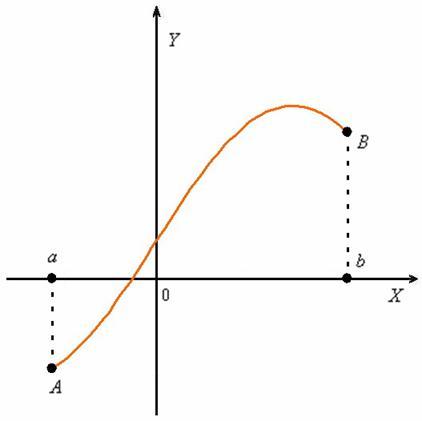
В предположении о непрерывности производной ![]() на
на ![]() , длина кривой
, длина кривой ![]() выражается формулой:
выражается формулой:
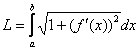 или компактнее:
или компактнее: 
Согласно геометрическому смыслу, длина не может быть отрицательной, и это заведомо гарантируется неотрицательностью подынтегральной функции ![]() (при разумеющемся условии
(при разумеющемся условии ![]() ). Таким образом, в данной задаче не возникает дополнительных хлопот по поводу того, как и где «петляет» график (выше оси, ниже оси и т.д.).
). Таким образом, в данной задаче не возникает дополнительных хлопот по поводу того, как и где «петляет» график (выше оси, ниже оси и т.д.).
Другой хорошей новостью является тот факт, что в практических примерах, как правило, не нужно строить чертежа. Это была единственная иллюстрация в статье, чтобы вы быстрее поняли, о чём вообще идёт речь. Впрочем, начнём с кривой, которую всем вбили в голову ещё в далёком детстве =)
Пример 1
Вычислить длину дуги параболы ![]() от точки
от точки ![]() до точки
до точки ![]()
Решение: принимая во внимание «иксовые» координаты точек, определяем пределы интегрирования ![]() и используем формулу:
и используем формулу:
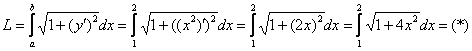
А вот и первый камень преткновения. Интеграл данного вида детально разобран в Примере № 5 урока Сложные интегралы, он интегрируется по частям и сводится к себе. Сначала удобно найти первообразную:
![]()
Интегрируем по частям:
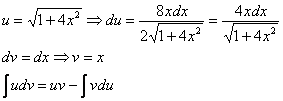
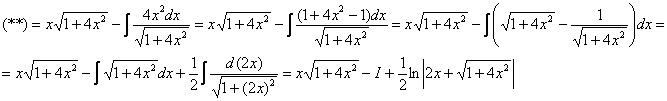
Таким образом:
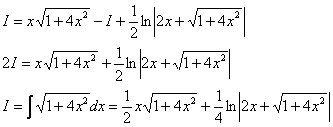
Открываем одиночной «звёздочкой» основное решение и используем формулу Ньютона-Лейбница:
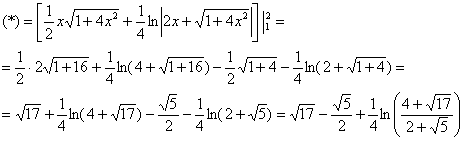
Ответ: 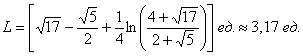
Скрупулёзно не проверял, но если взглянуть на параболу, то очень и очень похоже на правду. Громоздких и страшных результатов бояться не нужно, рАвно, как и длинных решений!
Следующие разминочные задачи для самостоятельного решения
Пример 2
Вычислить длину дуги полукубической параболы ![]() от точки
от точки ![]() до точки
до точки ![]()
Интеграл здесь будет значительно проще, чем в предыдущем примере. Однако за кажущейся простотой нередко скрывается коварство. Так, вроде бы похожее условие «Вычислить длину дуги полукубической параболы ![]() на промежутке
на промежутке ![]() » далеко не эквивалентно и приводит к совершенно другому ответу.
» далеко не эквивалентно и приводит к совершенно другому ответу.
Да, в рассматриваемом типе задач обычно не требуется выполнять чертёж, но всегда полезно, а иногда и очень важно знать, что это за линия и КАК выглядит её график ;-)
Пример 3
Вычислить длину дуги кривой ![]() ,
, ![]()
Это более распространённый вариант формулировки – когда промежуток интегрирования указан в виде двойного неравенства.
А что тут смущает? Люди без комплексов давно интегрируют по любой переменной, и я ещё в статье Объем тела вращения предлагал вам расширить свои взгляды =)
Обратная функция ![]() и её производная
и её производная ![]() непрерывны на отрезке
непрерывны на отрезке ![]() , поэтому применима зеркальная формула
, поэтому применима зеркальная формула 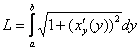 , где
, где ![]() и
и ![]() , естественно, уже «игрековые» пределы интегрирования.
, естественно, уже «игрековые» пределы интегрирования.
Кстати, в первом примере можно рассмотреть правую ветвь параболы ![]() с пределами интегрирования
с пределами интегрирования ![]() , правда, хрен редьки не слаще. Хотя любители оценят, интеграл получается трудный, но вполне реалистичный.
, правда, хрен редьки не слаще. Хотя любители оценят, интеграл получается трудный, но вполне реалистичный.
В следующем параграфе рассмотрим критически важную вещь, касающуюся всех задач урока:
Как найти длину дуги кривой, если линия задана параметрически?
Если линия задана параметрическими уравнениями ![]() , то при выполнении некоторых условий, на которых я не буду останавливаться, длина дуги кривой
, то при выполнении некоторых условий, на которых я не буду останавливаться, длина дуги кривой ![]() , которая прочерчивается при изменении параметра в пределах
, которая прочерчивается при изменении параметра в пределах ![]() , рассчитывается по формуле:
, рассчитывается по формуле:
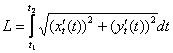 , где
, где ![]() – значения, определяющие точки
– значения, определяющие точки ![]() и
и ![]() .
.
В начале урока о площади и объёме при линиях, заданных параметрически, я обратил ваше внимание на тот факт, что параметрические уравнения могут «прорисовывать» кривую ![]() как слева направо, так и справа налево, из-за чего во втором случае «вылезает минус» и возникают небольшие технические затруднения. В рассматриваемой задаче мы от этого избавлены! Так как подынтегральная функция, как и в первом пункте, неотрицательна
как слева направо, так и справа налево, из-за чего во втором случае «вылезает минус» и возникают небольшие технические затруднения. В рассматриваемой задаче мы от этого избавлены! Так как подынтегральная функция, как и в первом пункте, неотрицательна ![]() , то заранее можно утверждать, что результата со знаком «минус» получиться не должно (понятно, при условии
, то заранее можно утверждать, что результата со знаком «минус» получиться не должно (понятно, при условии ![]() ).
).
Однако вместо «вопроса прорисовки дуги» у нас появляется другая почётная обязанность – беречь неотрицательность подынтегральной функции, как зеницу ока:
Пример 4
Вычислить длину дуги кривой 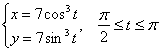
Решение: аналитические условия задают левую верхнюю дугу астроиды. Причём параметрические уравнения «прорисовывают» эту кривую справа налево, но, как я только что отметил, сейчас нас это не волнует, и асфальтный каток едет дальше.
Используем формулу 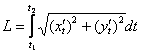 .
.
Сначала найдём производные:
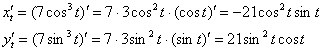
и упростим сумму их квадратов:
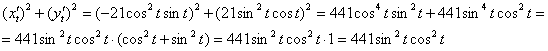
Это оптимальная во многих случаях техника решения, позволяющая не «таскать за собой» значки корня и интеграла с пределами интегрирования. Тем самым минимизируется риск что-нибудь потерять в громоздкой записи.
Гораздо удобнее «зарядить» в формулу готовую сумму:
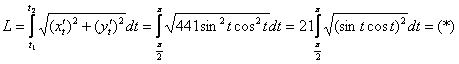
А вот теперь самый важный момент. Здесь нельзя «машинально» избавляться от корня и необходимо придерживаться следующего правила:
![]() , если функция
, если функция ![]() на промежутке
на промежутке ![]() ,
,
или ![]() , если
, если ![]() на данном промежутке.
на данном промежутке.
Эта «развилка» сохраняет неотрицательность подынтегральной функции, что соответствует геометрическому смыслу задачи.
На отрезке ![]() , следовательно, их произведение неположительное:
, следовательно, их произведение неположительное: ![]() и поэтому
и поэтому ![]()
Не понимаете, почему ![]() ? Посмотрите на их графики.
? Посмотрите на их графики.
Продолжаем, а точнее, заканчиваем решение:

Ответ: ![]()
Приятно, когда знаешь график функции, но вдвойне приятнее, когда можно эффективно проверить или даже заранее узнать ответ. Длина астроиды 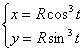 равна
равна ![]() . В нашей задаче
. В нашей задаче ![]() и мы рассчитали длину «четвертинки»:
и мы рассчитали длину «четвертинки»:
![]() , что и требовалось проверить.
, что и требовалось проверить.
Тренируемся самостоятельно:
Пример 5
Вычислить длину дуги кривой с точностью до двух знаков после запятой
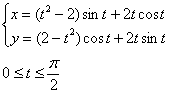
Примерный образец оформления задачи и в конце урока.
Продолжаем динамично закатывать асфальт:
Как найти длину дуги кривой, если линия задана в полярной системе координат?
Пусть кривая ![]() задана в полярных координатах уравнением
задана в полярных координатах уравнением ![]() , где
, где ![]() , и при этом значение
, и при этом значение ![]() определяет точку
определяет точку ![]() , а значение
, а значение ![]() – точку
– точку ![]() . Если на промежутке
. Если на промежутке ![]() функция
функция ![]() имеет непрерывную производную
имеет непрерывную производную ![]() , то длина кривой
, то длина кривой ![]() выражается следующей формулой:
выражается следующей формулой:
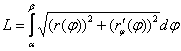
Условие ![]() логично и незыблемо. Это третья, похожая на предыдущую формула, которую мы незамедлительно оприходуем:
логично и незыблемо. Это третья, похожая на предыдущую формула, которую мы незамедлительно оприходуем:
Пример 6
Вычислить длину дуги кривой, заданную в полярной системе координат
![]() ,
, ![]()
Порядок и принципы решения точно такие же.
Используем формулу 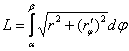 .
.
Найдём производную по «фи»:
![]()
Составим и максимально упростим подкоренное выражение:
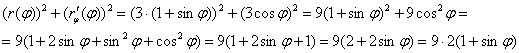
Заливаем топливо:
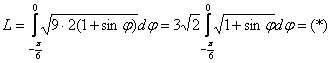
…мда, презабавно, всё время понижали-понижали степень, а теперь её надо повысить. Используем формулу двойного угла ![]() и основное тригонометрическое тождество
и основное тригонометрическое тождество ![]() , выцыганив тем самым заветный квадрат:
, выцыганив тем самым заветный квадрат:
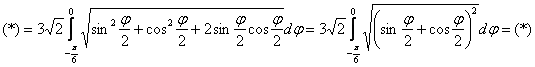
Теперь нужно разобраться с функцией ![]() на отрезке
на отрезке ![]() , чтобы правильно избавиться от корня. Я мысленно представляю график и вижу, что функция здесь положительна, но это очевидно далеко не всем, и в этой ситуации можно использовать нечто похожее на метод интервалов. Вычислим значение функции в какой-нибудь промежуточной точке, например, посерединке в точке
, чтобы правильно избавиться от корня. Я мысленно представляю график и вижу, что функция здесь положительна, но это очевидно далеко не всем, и в этой ситуации можно использовать нечто похожее на метод интервалов. Вычислим значение функции в какой-нибудь промежуточной точке, например, посерединке в точке ![]() :
:
![]() , а значит,
, а значит, ![]() и в любой точке интервала
и в любой точке интервала ![]() . К слову, и на концах тоже.
. К слову, и на концах тоже.
Примечание: строго говоря, надо ещё добавить, что уравнение ![]() не имеет корней на данном интервале.
не имеет корней на данном интервале.
Таким образом, вынесение из-под корня проходит без всяких последствий. …Не хотел вам рассказывать об одном нехорошем методе решения, но таки поделюсь – всё равно догадаетесь, по себе знаю =) На черновике считаем интеграл 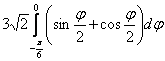 и если получился отрицательный результат, то на чистовике ставим перед интегралом «минус». И никаких запарок с рассуждениями.
и если получился отрицательный результат, то на чистовике ставим перед интегралом «минус». И никаких запарок с рассуждениями.
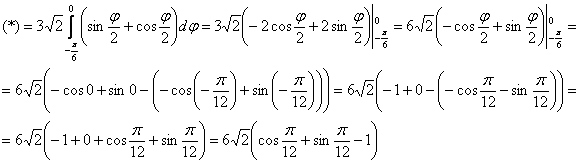
Ответ: ![]()
Я решил эту задачу много лет назад именно таким способом и недавно, подбирая примеры к уроку, нашёл более симпатичное решение, идея которого состоит в использовании формулы приведения ![]() и дальнейшего повышения степени по избитой формуле
и дальнейшего повышения степени по избитой формуле ![]() . Там получается ответ в другом виде, но численно результаты совпадают. Такое тоже бывает.
. Там получается ответ в другом виде, но численно результаты совпадают. Такое тоже бывает.
Затем я углубился в свой архив и нашёл ещё много чего знакомого. Такое впечатление, что сборник Кузнецова – очень популярный поставщик задач по приложениям определённого интеграла в контрольные работы. И в разделе IV-Интегралы вы можете найти порядка сотни прорешанных примеров по теме (Задачи 17-19), велика вероятность, что найдётся и ваш пример!
Успокоительная миниатюра для самостоятельного решения:
Пример 7
Вычислить длину дуги кривой, заданную в полярной системе координат
![]() ,
, ![]()
Хочется сказать ещё что-нибудь ласковое, но, к сожалению, я тороплюсь, сегодня пятница и мне тоже хочется погулять =)
Желаю успехов!
Решения и ответы:
Пример 2: Решение: пределы интегрирования: ![]() . Из условия следует, что требуется вычислить длину дуги верхней ветви
. Из условия следует, что требуется вычислить длину дуги верхней ветви ![]() .
.
Найдём производную: ![]() .
.
По формуле:
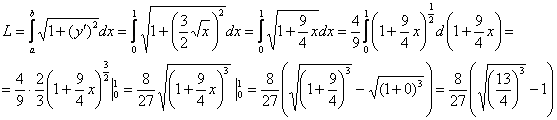
Ответ: 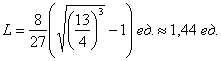
Пример 3: Решение: найдём производную:
![]()
Таким образом:

(1) Используем тригонометрическую формулу ![]()
(2) При вынесении из-под корня необходимо, чтобы подынтегральная функция осталась положительной:![]() . Так как
. Так как ![]() на отрезке интегрирования, то:
на отрезке интегрирования, то: ![]() .
.
(3) Данный интеграл разобран в Примере 18 статьи Сложные интегралы.
Ответ: ![]()
Пример 5: Решение: используем формулу 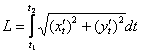 .
.
Найдём производные:
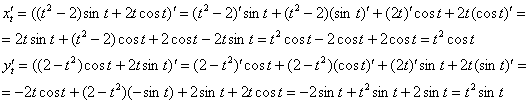
Таким образом:
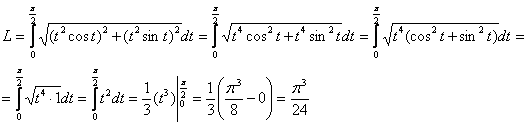
Примечание: ![]() при любом значении
при любом значении ![]() .
.
Ответ: ![]()
Пример 7: Решение: используем формулу:

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright