


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Правила Лопиталя. Примеры решений
Представьте стаю воробьёв с выпученными глазами. Нет, это не гром, не ураган и даже не маленький мальчик с рогаткой в руках. Просто в самую гущу птенчиков летит огромное-огромное пушечное ядро. Именно так правила Лопиталя расправляются с пределами, в которых имеет место неопределённость ![]() или
или ![]() .
.
Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности, не случайно в сборниках задач, на контрольных работах, зачётах часто встречается устойчивый штамп: «вычислить предел, не пользуясь правилом Лопиталя». Выделенное жирным шрифтом требование можно с чистой совестью приписать и к любому пределу уроков Пределы. Примеры решений, Замечательные пределы. Методы решения пределов, Замечательные эквивалентности, где встречается неопределённость «ноль на ноль» либо «бесконечность на бесконечность». Даже если задание сформулировано коротко – «вычислить пределы», то негласно подразумевается, что вы будете пользоваться всем, чем угодно, но только не правилами Лопиталя.
Всего правил два, и они очень похожи друг на друга, как по сути, так и по способу применения. Кроме непосредственных примеров по теме, мы изучим и дополнительный материал, который будет полезен в ходе дальнейшего изучения математического анализа.
Сразу оговорюсь, что правила будут приведены в лаконичном «практическом» виде, и если вам предстоит сдавать теорию, рекомендую обратиться к учебнику за более строгими выкладками.
Первое правило Лопиталя
Рассмотрим функции ![]() , которые бесконечно малЫ в некоторой точке
, которые бесконечно малЫ в некоторой точке ![]() . Если существует предел их отношений
. Если существует предел их отношений ![]() , то в целях устранения неопределённости
, то в целях устранения неопределённости ![]() можно взять две производные – от числителя и от знаменателя. При этом:
можно взять две производные – от числителя и от знаменателя. При этом: ![]() , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
, то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел ![]() тоже должен существовать, в противном случае правило не применимо.
тоже должен существовать, в противном случае правило не применимо.
Что следует из вышесказанного?
Во-первых, необходимо уметь находить производные функций, и чем лучше – тем лучше =)
Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного 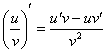 !!!
!!!
И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость ![]() .
.
Вернёмся к Примеру 5 первой статьи о пределах, в котором был получен следующий результат:
![]()
К неопределённости 0:0 применим первое правило Лопиталя:
![]()
Как видите, дифференцирование числителя и знаменателя привело нас к ответу с пол оборота: нашли две простые производные, подставили в них «двойку», и оказалось, что неопределённость бесследно исчезла!
Не редкость, когда правила Лопиталя приходится применять последовательно два или бОльшее количество раз (это относится и ко второму правилу). Вытащим на ретро-вечер Пример 2 урока о замечательных пределах:
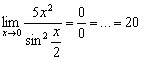
На двухъярусной кровати снова прохлаждаются два бублика. Применим правило Лопиталя:
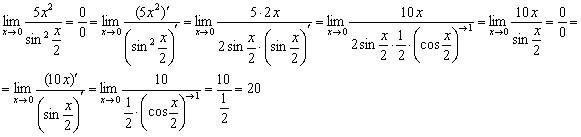
Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции. После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).
Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные, следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам. Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.
Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через замечательные эквивалентности.
Второе правило Лопиталя
Брат-2 борется с двумя спящими восьмёрками ![]() . Аналогично:
. Аналогично:
Если существует предел отношения бесконечно больших в точке ![]() функций:
функций: ![]() , то в целях устранения неопределённости
, то в целях устранения неопределённости ![]() можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом:
можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: ![]() , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
, то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел ![]() должен существовать
должен существовать
Опять же, в различных практических примерах значение ![]() может быть разным, в том числе, бесконечным. Важно, чтобы была неопределённость
может быть разным, в том числе, бесконечным. Важно, чтобы была неопределённость ![]() .
.
Проверим Пример №3 первого урока: ![]() . Используем второе правило Лопиталя:
. Используем второе правило Лопиталя:
![]()
Однако для Примера №2 ![]() той же статьи проверка данным способом будет весьма муторна. Тут придётся использовать правило Лопиталя три раза подряд (экспериментаторы могут попробовать). На самом деле ответ лежит на поверхности и почти мгновенно определяется устно (см. статью Методы решения пределов).
той же статьи проверка данным способом будет весьма муторна. Тут придётся использовать правило Лопиталя три раза подряд (экспериментаторы могут попробовать). На самом деле ответ лежит на поверхности и почти мгновенно определяется устно (см. статью Методы решения пределов).
Коль скоро речь зашла о великанах, разберём два каноничных предела:
Пример 1
Вычислить предел
![]()
Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:
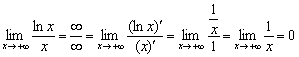
Таким образом, линейная функция более высокого порядка роста, чем логарифм с основанием бОльшим единицы (![]() и т.д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция
и т.д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция ![]() растёт достаточно медленно и её график является более пологим относительно того же «икса».
растёт достаточно медленно и её график является более пологим относительно того же «икса».
Пример 2
Вычислить предел
![]()
Ещё один примелькавшийся кадр. В целях устранения неопределённости ![]() , используем правило Лопиталя, причём, два раза подряд:
, используем правило Лопиталя, причём, два раза подряд:
![]()
Показательная функция, с основанием, бОльшим единицы (![]() и т.д.) более высокого порядка роста, чем степенная функция с положительной степенью.
и т.д.) более высокого порядка роста, чем степенная функция с положительной степенью.
Похожие пределы встречаются в ходе полного исследования функции, а именно, при нахождении асимптот графиков. Также замечаются они и в некоторых задачах по теории вероятностей. Советую взять на заметку два рассмотренных примера, это один из немногих случаев, когда лучше дифференцирования числителя и знаменателя ничего нет.
Далее по тексту я не буду разграничивать первое и второе правило Лопиталя, это было сделано только в целях структурирования статьи. Вообще, с моей точки зрения, несколько вредно излишне нумеровать математические аксиомы, теоремы, правила, свойства, поскольку фразы вроде «согласно следствию 3 по теореме 19…» информативны только в рамках того или иного учебника. В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел.
Продолжаем разрабатывать тему, которую нам подкинул член Парижской академии наук маркиз Гийом Франсуа де Лопиталь. Статья приобретает ярко выраженную практическую окраску и в достаточно распространённом задании требуется:
Вычислить предел, используя правило Лопиталя
Для разминки разберёмся с парой небольших воробушков:
Пример 3
Вычислить предел по правилу Лопиталя
![]()
Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:
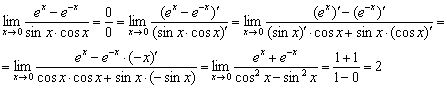
В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения ![]() .
.
Рассмотренный пример разруливается и через замечательные пределы, похожий случай разобран в конце статьи Сложные пределы.
Пример 4
Вычислить предел по правилу Лопиталя
![]()
Это пример для самостоятельного решения. Нормально пошутил =)
Типична ситуация, когда после дифференцирования получаются трех- или четырёхэтажные дроби:
Пример 5
Вычислить предел, используя правило Лопиталя
![]()
Напрашивается применение замечательной эквивалентности, но путь жёстко предопределён по условию:
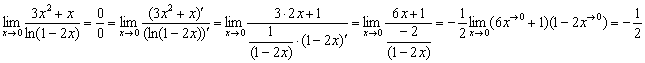
После дифференцирования настоятельно рекомендую избавляться от многоэтажности дроби и проводить максимальные упрощения. Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: 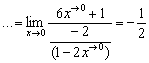 , но в некоторых пределах запутаются даже отличники.
, но в некоторых пределах запутаются даже отличники.
Пример 6
Вычислить предел, используя правило Лопиталя
![]()
Пример 7
Вычислить предел, используя правило Лопиталя
![]()
Это примеры для самостоятельного решения. В Примере 6 можно ничего не упрощать, слишком уж простой получается после дифференцирования дробь. А вот в Примере 7 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными. Полное решение и ответ в конце урока. Если возникли затруднения – тригонометрическая таблица в помощь.
И, упрощения совершенно необходимы, когда после дифференцирования неопределённость не устранена.
Пример 8
Вычислить предел, используя правило Лопиталя
![]()
Поехали:
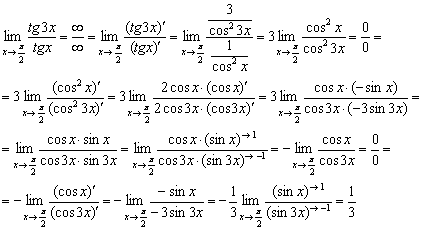
Интересно, что первоначальная неопределённость ![]() после первого дифференцирования превратилась в неопределённость
после первого дифференцирования превратилась в неопределённость ![]() , и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при
, и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при ![]() , а
, а ![]() , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.
, поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.
На днях мне попалось любопытное задание:
Пример 9
Вычислить предел функции, используя правило Лопиталя
![]()
Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.
Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….
В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида ![]() .
.
Расправа с неопределённостью ![]() подробно разобрана в Примерах №№9-13 урока Методы решения пределов. Давайте для проформы ещё один:
подробно разобрана в Примерах №№9-13 урока Методы решения пределов. Давайте для проформы ещё один:
Пример 10
Вычислить предел функции, используя правило Лопиталя
![]()
На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость ![]() в неопределённость
в неопределённость ![]() . А затем заряжаем правило Лопиталя:
. А затем заряжаем правило Лопиталя:
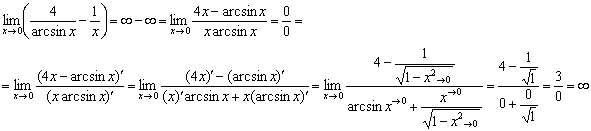
Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.
Неопределённость ![]() тоже не сопротивляется превращению в
тоже не сопротивляется превращению в ![]() или
или ![]() :
:
Пример 11
Вычислить предел функции с помощью правила Лопиталя
![]()
Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций. Как вы помните, графика «классического» логарифма не существует слева от оси ![]() , таким образом, мы можем приближаться к нулю только справа.
, таким образом, мы можем приближаться к нулю только справа.
Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью ![]() . На первом шаге делаем дробь трёхэтажной, получая неопределённость
. На первом шаге делаем дробь трёхэтажной, получая неопределённость ![]() , далее решение идёт по шаблонной схеме:
, далее решение идёт по шаблонной схеме:
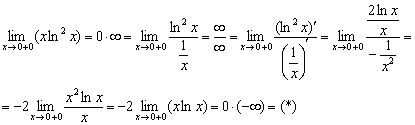
После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость ![]() . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости
. Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости ![]() применяем правило Лопиталя ещё раз:
применяем правило Лопиталя ещё раз:
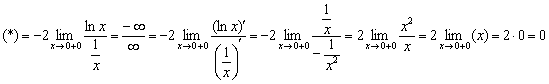
Готово.
Исходный предел можно было попытаться свести к двум бубликам:
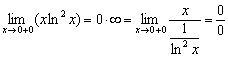
Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.
Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести ![]() – к «нулю на ноль» или к «бесконечности на бесконечность».
– к «нулю на ноль» или к «бесконечности на бесконечность».
В свою очередь на огонёк ![]() подтягиваются
подтягиваются собутыльники ![]() и более экзотические товарищи
и более экзотические товарищи ![]() . Метод трансформации прост и стандартен:
. Метод трансформации прост и стандартен:
Пример 12
Вычислить предел функции с помощью правила Лопиталя
![]()
Для устранения неопределённости ![]() используем основное логарифмическое тождество:
используем основное логарифмическое тождество: ![]() . В данном случае
. В данном случае ![]() :
:
![]()
На предпоследнем шаге, согласно известному школьному свойству, «сносим» синус из степени за пределы логарифма, получая произведение ![]() . На последнем шаге перемещаем значок предела в показатель (поскольку экспоненциальная функция непрерывна, да и предел относится, прежде всего, к верхнему этажу).
. На последнем шаге перемещаем значок предела в показатель (поскольку экспоненциальная функция непрерывна, да и предел относится, прежде всего, к верхнему этажу).
Чтобы не мельчить, вычислим предел показателя отдельно:
![]()
С неопределённостью ![]() разбираемся уже знакомым способом – делаем дробь трёхэтажной, получая долгожданную неопределённость
разбираемся уже знакомым способом – делаем дробь трёхэтажной, получая долгожданную неопределённость ![]() , к которой применимо правило Лопиталя:
, к которой применимо правило Лопиталя:
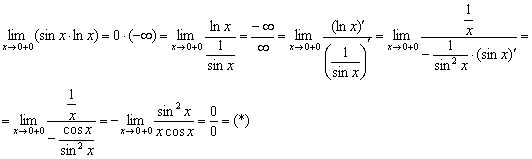
Метаморфозы продолжаются, теперь вылезла неопределённость «ноль на ноль». В принципе, можно избавиться от косинуса, указав, что он стремится к единице. Но мудрая стратегия заключается в том, чтобы никто ни до чего не докопался. Поэтому сразу применим правило Лопиталя, как этого требует условие задачи:
![]()
Не торопитесь, предел не равен нулю! Мы вычислили только предел показателя. В конце решения главное не забыть про экспоненту, я сейчас сам чуть про неё не забыл =) Окончательно:
![]()
В ряде случаев после использование основного логарифмического тождества удаётся миновать неопределённость ![]() :
:
Пример 13
Вычислить предел по правилу Лопиталя
![]()
Очередной папуас ![]() тоже сдаётся перед формулой
тоже сдаётся перед формулой ![]() . В данном случае
. В данном случае ![]() :
:
![]()
В результате сразу получена неопределённость ![]() , что облегчает задачу. Предел показателя для удобства вычислим отдельно:
, что облегчает задачу. Предел показателя для удобства вычислим отдельно:
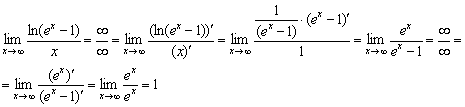
В итоге:
![]()
Аналогичное задание для самостоятельного решения:
Пример 14
Вычислить предел по правилу Лопиталя
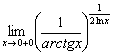
Полное решение и ответ в конце урока.
Предел с неопределённостью ![]() по правилу Лопиталя, если честно, у себя не нашёл, но для полноты картины решим многострадальный шестой пример урока Замечательные пределы:
по правилу Лопиталя, если честно, у себя не нашёл, но для полноты картины решим многострадальный шестой пример урока Замечательные пределы:
Пример 15
Вычислить с помощью правила Лопиталя
![]()
Решайте =)
В заключение хочу успокоить гринписовцев – ни один воробей от оружия серьёзно не пострадал, пределы – птицы юркие, да и ядра формы обтекаемой. Вспоминаем обычное требование: «…не пользуясь правилом Лопиталя». С беспощадной действительностью соприкоснёмся в статье Сложные пределы.
Желаю успехов!
Решения и ответы:
Пример 4
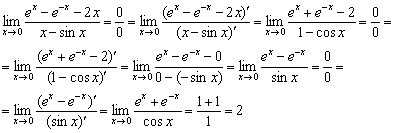
Пример 6
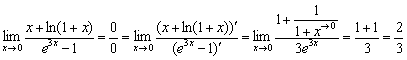
Пример 7
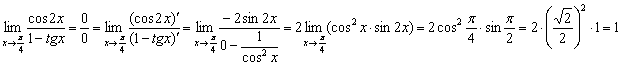
Пример 9
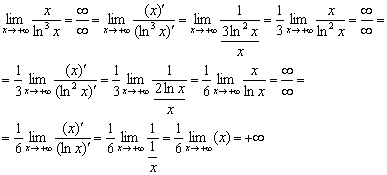
Пример 14
Используем основное логарифмическое тождество и преобразование ![]() :
:
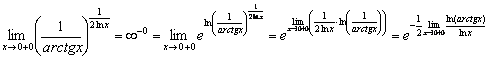
Вычислим предел показателя:
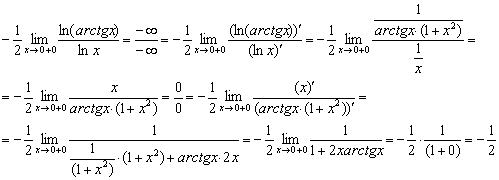
Таким образом: 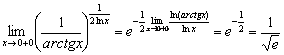
Пример 15
Используем основное логарифмическое тождество:

Вычислим предел показателя:
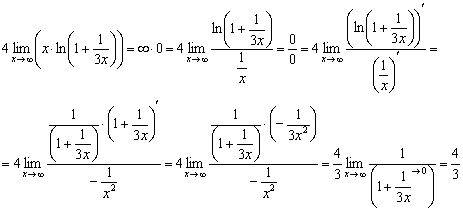
Таким образом: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright