


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Переход к новому базису и к новой системе координат
Эта небольшая статья появилась на свет значительно позже большинства моих уроков по аналитической геометрии, и предназначена она для более или менее подготовленных читателей, которые знакомы с векторами, матрицами и обладают навыками решения основных тематических задач. Впрочем, что означает «более или менее подготовленных»? …Если Вы понимаете, чем отличается базис от системы координат – тогда смело читайте дальше! Потому что будет очень интересно – сегодня мы станем очевидцами самой настоящей революции в мире векторов! Такие эпохальные события происходят не каждый день, и поэтому нет ничего удивительного в том, что задачи перехода к новому базису и перехода к новой системе координат заметно реже встречаются на практике. Однако, это как раз та тема, которая вызывает наибольшую путаницу и недопонимание у студентов. Дело осложняется ещё и тем, что в различных источниках информации используются разные схемы подачи материала и разные обозначения
Но сейчас пришло время окончательно вас запутать «расставить все точки над i» и расстановка этих точек начинается с «плоского» случая. Кстати, и буква нужная сразу вспомнилась. Рассмотрим привычный ортонормированный базис ![]() и два подопытных вектора:
и два подопытных вектора:
![]()
или: ![]() .
.
Как вы прекрасно знаете, любой другой вектор ![]() плоскости тоже можно разложить по базисным векторам:
плоскости тоже можно разложить по базисным векторам: ![]() (причём единственным образом) и записать коэффициенты этого разложения (координаты) в скобках:
(причём единственным образом) и записать коэффициенты этого разложения (координаты) в скобках: ![]()
И всё бы было тихо-спокойно, но мирную жизнь векторов нарушает появление другого базиса…. Почему он появляется? Так нужно в ряде задач высшей математики. И не только математики.
В качестве демонстрационного базиса можно взять любую пару неколлинеарных векторов, но для удобства объяснений я рассмотрю следующий ортогональный базис ![]() :
:
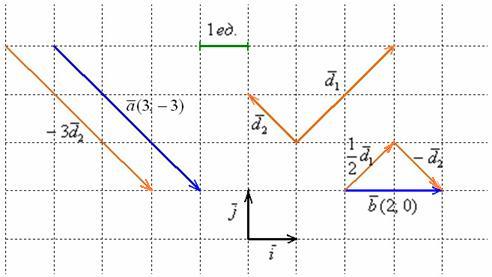
Обратите внимание, что новый базис не является ортонормированным – длины его векторов отличны от единицы: ![]()
Наверное, все понимают происходящие события – когда меняется власть, то все подстраиваются под эту власть. Таким образом, наша задача состоит в том, чтобы найти разложения тех же самых векторов по НОВОМУ базису.
На иллюстрации хорошо видно готовые результаты:
![]() , то есть
, то есть ![]() – это координаты вектора «а» в базисе
– это координаты вектора «а» в базисе ![]() ;
;
![]() и
и ![]() – есть координаты вектора «бэ» в новом базисе.
– есть координаты вектора «бэ» в новом базисе.
Примечание: заметьте, что «условные единицы» нового базиса в ![]() и
и ![]() раз больше единицы исходного базиса.
раз больше единицы исходного базиса.
Но всё хорошо видно лишь потому, что я подобрал простые базисы и удобные векторы, и поэтому нам нужно изучить аналитический метод перехода от одного базиса к другому. Очевидно, что для осуществления такого перехода нужно как-то связать векторы старого и нового базиса. Первое, что приходит в голову – это разложить векторы «пришлой власти» по базису ![]() :
:
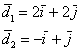
…если вам не понятно, откуда берутся все эти разложения – срочно изучать/повторять «школьные» действия с векторами!
Коэффициенты разложений напрашивается записать в матрицу: ![]() . Или так:
. Или так: ![]() . …В верном направлении движемся, товарищи! И ту, и другую матрицу называют матрицей перехода от базиса
. …В верном направлении движемся, товарищи! И ту, и другую матрицу называют матрицей перехода от базиса ![]() к базису
к базису ![]() . По техническим причинам чаще встречается 2-й вариант – когда коэффициенты «укладывают» в столбцы.
. По техническим причинам чаще встречается 2-й вариант – когда коэффициенты «укладывают» в столбцы.
Но от красивой записи толку мало, и сейчас нам предстоит разобраться, как связаны между собой координаты ![]() произвольного вектора
произвольного вектора ![]() в старом базисе
в старом базисе ![]() с его соответствующими координатами
с его соответствующими координатами ![]() в новом базисе
в новом базисе ![]() .
.
! Штрихи здесь не имеют никакого отношения к производным!
Для решения нашей задачи подставим разложения ![]() во 2-е равенство, раскроем скобки и перегруппируем слагаемые:
во 2-е равенство, раскроем скобки и перегруппируем слагаемые:
![]()
Таким образом, с одной стороны, в нашем распоряжении есть старое разложение ![]() , но с другой стороны мы получили
, но с другой стороны мы получили ![]() . Поскольку разложение вектора по базису единственно, то справедливы следующие равенства:
. Поскольку разложение вектора по базису единственно, то справедливы следующие равенства:
![]()
С помощью полученных соотношений можно найти СТАРЫЕ координаты, если известны новые.
Запишем формулы в виде простейшего матричного уравнения:
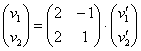
и выполним проверку, тестируя наши подопытные векторы «а» и «бэ»:
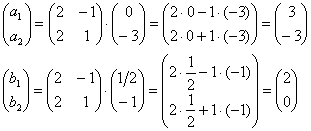
Что и требовалось проверить. Надеюсь, ни у кого не возникло проблем с матричным умножением. Хотя, в случае аварийных недоразумений всегда можно подставить новые координаты в равенства ![]() и получить те же самые результаты.
и получить те же самые результаты.
Всё хорошо, всё правильно, но нам-то нужно наоборот – из старых координат получить новые. Давайте присмотримся к нашему матричному уравнению 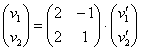 …. В его середине находится матрица с координатами векторов
…. В его середине находится матрица с координатами векторов ![]() , которые записаны в столбцы. И, обозначив
, которые записаны в столбцы. И, обозначив 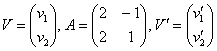 , перепишем уравнение в компактном виде:
, перепишем уравнение в компактном виде:
![]()
Для того чтобы выразить новые координаты через старые, умножим обе части на ![]() слева:
слева:
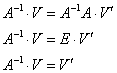
В результате ситуация разрешилась самым благоприятным образом:
![]()
Теперь нужно найти обратную матрицу. Так как векторы базиса линейно независимы, то определитель ![]() и обратная матрица заведомо существует. Я не буду подробно расписывать процесс её нахождения (с которым можно ознакомиться по ссылке) и сразу приведу готовый результат:
и обратная матрица заведомо существует. Я не буду подробно расписывать процесс её нахождения (с которым можно ознакомиться по ссылке) и сразу приведу готовый результат:
![]() – тот редкий случай, когда дробь целесообразно затолкать в матрицу.
– тот редкий случай, когда дробь целесообразно затолкать в матрицу.
Пользуясь уравнением 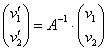 , вычислим координаты векторов
, вычислим координаты векторов ![]() в базисе
в базисе ![]() :
:
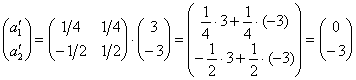 , то есть
, то есть ![]() ;
;
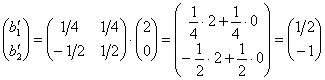 , то есть
, то есть ![]() .
.
Желающие могут протестировать другие «сподручные» векторы и свериться с чертежом.
Нетрудно догадаться, что в столбцах полученной матрицы ![]() находятся коэффициенты разложения векторов старого базиса по векторам нового базиса:
находятся коэффициенты разложения векторов старого базиса по векторам нового базиса:
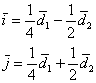
(убедитесь по чертежу в справедливости этих разложений)
и матрица ![]() называется (именно так!) матрицей перехода от базиса
называется (именно так!) матрицей перехода от базиса ![]() к базису
к базису ![]() .
.
Из статьи о линейных преобразованиях вы узнаете (или уже знаете), что любой квадратной матрице «два на два» соответствует определённое преобразование (грубо говоря, искажение) плоскости, и, как видите, невырожденная матрица «два на два» может иметь и другой геометрический смысл. Любопытные читатели непременно проанализируют, какие линейные преобразования задают рассмотренные матрицы.
Систематизируем алгоритм решения данной задачи: итак, заданы два произвольных базиса плоскости ![]() , при этом векторы 2-го базиса выражены через векторы 1-го:
, при этом векторы 2-го базиса выражены через векторы 1-го:
![]()
! Обозначения: в данном контексте двойные подстрочные индексы имеют следующий смысл: 1-я цифра обозначает номер координаты, 2-я цифра – номер вектора:
![]() – 1-я координата 1-го вектора (вектора
– 1-я координата 1-го вектора (вектора ![]() ),
), ![]() – 2-я координата 1-го вектора;
– 2-я координата 1-го вектора;
![]() – 1-я координата 2-го вектора (вектора
– 1-я координата 2-го вектора (вектора ![]() ),
), ![]() – 2-я координата 2-го вектора.
– 2-я координата 2-го вектора.
Следует отметить, что в других источниках информации обозначения могут быть другими, я выбрал вариант, который мне показался наиболее понятным.
В базисе ![]() дан вектор
дан вектор ![]() . Требуется найти его координаты
. Требуется найти его координаты ![]() в базисе
в базисе ![]() .
.
На первом шаге составляем матричное уравнение, при этом коэффициенты разложений ![]() «укладываем» в столбцы матрицы:
«укладываем» в столбцы матрицы: 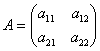 (векторы
(векторы ![]() следует «перебирать» строго по порядку!):
следует «перебирать» строго по порядку!):
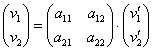 или, если компактнее:
или, если компактнее: ![]()
Уравнение, кстати, легко преобразовать в формулы, выражающие старые координаты через новые. Выполняем матричное умножение:
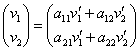
Две матрицы равны, если равны их соответствующие элементы:
![]()
Читателям, углубленно изучающим математику, рекомендую вывести эти формулы самостоятельно (по аналогии конкретных рассуждений в разобранном примере).
Но возвращаемся к нашей задаче. Она элементарна! Находим обратную матрицу ![]() и, вычисляя произведение
и, вычисляя произведение ![]() , получаем координаты вектора
, получаем координаты вектора ![]() в базисе
в базисе ![]() :
:
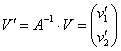
Простота простотой, но в действительности эта задача вызывает серьёзные затруднения у многих студентов. Связано это, видимо, с не наглядностью изложения материала. Как правило, в типовом источнике можно увидеть два «косых» базиса (если чертёж есть вообще), и вкупе со всеми этими штрихами (популярный стиль), непонятными индексами возникает только одно желание – захлопнуть книгу/закрыть окно. И в демонстрационном примере я специально рассмотрел два «хороших» базиса – чтобы не наглядный материал превратить в ненаглядный =)
…так чувствуется, вам уже не терпится что-нибудь порешать! Пространственный случай для самостоятельного изучения:
Задача 1
1) В трехмерном пространстве заданы базисы ![]() , причём:
, причём:
![]()
Записать два матричных уравнения, которые связывают координаты ![]() вектора
вектора ![]() в базисе
в базисе ![]() с его координатами
с его координатами ![]() в базисе
в базисе ![]() .
.
2) ![]() .
.
Найти разложение вектора ![]() по базису
по базису ![]()
Краткое решение и ответы в конце урока.
Следует отметить, что формулировка этой задачи вовсе не подразумевает, что речь идёт именно о геометрических векторах. Это могут быть векторы и другой природы. Я очень надеюсь, что на данный момент вы всё-таки почитали мои статьи по высшей алгебре и добрались до статьи о линейных преобразованиях, где я обобщил понятие вектора. Однако сейчас у нас на повестке дня аналитическая геометрия, и поэтому я перехожу к рассмотрению второго вопроса:
Переход к новой системе координат
Это не то же самое, что переход к новому базису! Хотя задача родственная.
Наверняка первый чертёж урока вызвал у вас мысль, что «чего-то здесь не хватает». И действительно, коль скоро речь шла о базисах, то нам было вполне достаточно векторов. А вектор – это птица свободная, и на иллюстрации их вообще можно было расположить как угодно. Но во многих случаях существует потребность учесть преобразование координат точек, и по этой причине возникает необходимость «застолбить» начальную точку отсчёта (начало координат), которая в тандеме с базисными векторами порождает аффинную систему координат.
Рассмотрим две аффинные системы координат плоскости: ![]() . Первую систему по нестарой памяти назовём старой, вторую – новой, и, как водится, запишем традиционное разложение:
. Первую систему по нестарой памяти назовём старой, вторую – новой, и, как водится, запишем традиционное разложение:
![]()
Не углубляясь в книжные рассуждения, я сразу приведу готовые формулы, позволяющие узнать старые координаты ![]() произвольной точки
произвольной точки ![]() плоскости, если известны её новые координаты
плоскости, если известны её новые координаты ![]() :
:
![]() , где
, где ![]() – координаты точки
– координаты точки ![]() в старой системе координат.
в старой системе координат.
Данные равенства называются формулами преобразования аффинной системы координат, и в них легко просматривается знакомая матрица 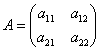 .
.
Вернёмся к нашим ненаглядным базисам =), на основе которых построим две системы координат: ![]() . В качестве начала новой системы координат я выберу точку
. В качестве начала новой системы координат я выберу точку ![]() :
:
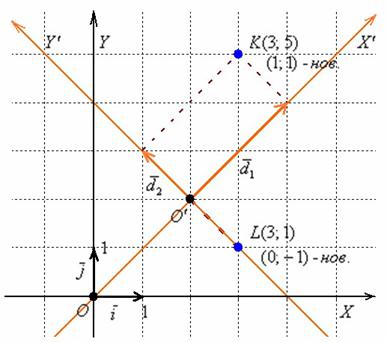
Теперь «укладываем» коэффициенты разложений ![]() в «столбцы» формул
в «столбцы» формул ![]() :
:
![]()
Подопытные точки опять же – синие и пушистые =) Пожалуйста, наклоните голову на 45 градусов влево и убедитесь, что в «оранжевой» системе координат точка ![]() имеет координаты
имеет координаты ![]() , а точка
, а точка ![]() – координаты
– координаты ![]() (коричневые пунктирные линии). Вычислим координаты данных точек в исходном базисе
(коричневые пунктирные линии). Вычислим координаты данных точек в исходном базисе ![]() :
:
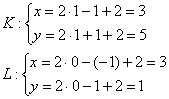
В чём и требовалось убедиться.
Однако здесь опять всё «задом наперёд» – ведь в подавляющем большинстве случаев новые-то координаты нам как раз не известны. На очереди знакомая схема действий. Запишем формулы ![]() в виде матричного уравнения:
в виде матричного уравнения:
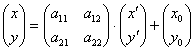 или, если компактнее:
или, если компактнее: ![]()
И с помощью стандартных преобразований выражаем столбец новых координат:
![]() , где
, где 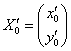 – координаты точки
– координаты точки ![]() в новом базисе. Данный столбец рассчитывается по формуле
в новом базисе. Данный столбец рассчитывается по формуле ![]() .
.
В нашем примере обратная матрица уже найдена в предыдущем параграфе ![]() и осталось как раз узнать этот столбец:
и осталось как раз узнать этот столбец:
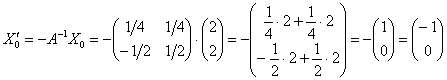
Пожалуйста, снова наклоните голову влево на ![]() и убедитесь, что в новой («оранжевой») системе координат точка
и убедитесь, что в новой («оранжевой») системе координат точка ![]() обладает именно координатами
обладает именно координатами ![]() .
.
Запишем рабочее матричное уравнение ![]() и рассчитаем координаты точек
и рассчитаем координаты точек ![]() в новой системе координат:
в новой системе координат:
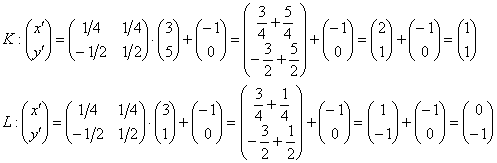
Рассмотренные формулы работают для произвольных аффинных систем плоскости, однако в практических задачах особую важность имеет переход от прямоугольной декартовой системы координат ![]() к другой декартовой системе
к другой декартовой системе ![]() . Но перед тем, как приступить к изучению этого частного случая, я расскажу вам о том, о чём многие слышали, но стеснялись спросить:))
. Но перед тем, как приступить к изучению этого частного случая, я расскажу вам о том, о чём многие слышали, но стеснялись спросить:))
Ориентация плоскости
У плоскости может быть две ориентации. Левая. И правая. Первая ориентация задаётся левоориентированным базисом и, как следствие, левой системой координат, вторая – соответственно, правоориентированным базисом и правой системой.
По сложившейся традиции разбираться будем на пальцах: разверните ладони вверх и прижмите к ним все пальцы, кроме указательных и больших. Теперь совместите указательные пальцы. Большие пальцы при этом расположатся по разные стороны. Наоборот: совместите большие пальцы – тогда по разные от них стороны окажутся пальцы указательные. Это признак того, что символические базисы и порождаемые ими системы координат имеют разную ориентацию.
Если большой палец символизирует 1-й вектор базиса, а указательный палец – 2-й вектор базиса (ладони развёрнуты вверх),то базис правой руки принято считать правоориентированным, а базис левой руки – левоориентированным.
Так, например, наша «школьная» система координат ![]() является правой. Как в этом убедиться? Совместите большой палец правой руки с вектором
является правой. Как в этом убедиться? Совместите большой палец правой руки с вектором ![]() (первым вектором базиса). Тогда указательный палец будет смотреть в сторону вектора
(первым вектором базиса). Тогда указательный палец будет смотреть в сторону вектора ![]() , и это признак того, что базис правоориентирован.
, и это признак того, что базис правоориентирован.
Вообще, рассматриваемое понятие весьма удачно характеризует осевая (зеркальная) симметрия, которая меняет ориентацию плоскости. Изобразим в прямоугольной системе брата нашего меньшего и отобразим его симметрично относительно оси ординат:
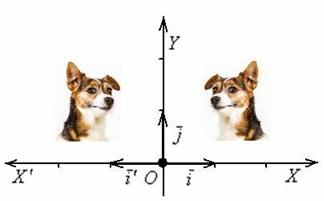
Совершенно понятно, что как ни перемещай, как ни крути изображения – совместить их не удастся. Это и есть эффект разной ориентации. Обратите внимание, что 1-й координатный вектор тоже подвергся отражению, и левая система ![]() задала левую ориентацию плоскости – координатная ось
задала левую ориентацию плоскости – координатная ось ![]() «развернулась» в противоположную сторону и положительные значения стали отсчитываться справа налево. И, кстати, ничто не мешает вести отсчёт именно так! Но тут нас вряд ли поймут – не зря же ориентацию назвали левой =) Хотя чисто «технически» она ничем не хуже.
«развернулась» в противоположную сторону и положительные значения стали отсчитываться справа налево. И, кстати, ничто не мешает вести отсчёт именно так! Но тут нас вряд ли поймут – не зря же ориентацию назвали левой =) Хотя чисто «технически» она ничем не хуже.
Если Тузика отобразить симметрично относительно оси ![]() , то получим другую левую систему
, то получим другую левую систему ![]() , в которой единичный вектор
, в которой единичный вектор ![]() смотрит вниз.
смотрит вниз.
Взаимную ориентацию двух базисов (а значит и взаимную ориентацию порожденных ими систем координат) можно установить аналитически: если определитель матрицы перехода от одного базиса к другому больше нуля, то базисы ориентированы одинаково (оба левые или оба правые), в противном случае они имеют разную ориентацию. Так, в демонстрационном примере нашего урока ![]() , значит, базисы
, значит, базисы ![]() ориентированы одинаково. И поскольку «школьный» базис считается правым, то
ориентированы одинаково. И поскольку «школьный» базис считается правым, то ![]() – тоже правый (впрочем, это и так очевидно). В Задаче 1 (пункт 2) определитель матрицы перехода отрицателен:
– тоже правый (впрочем, это и так очевидно). В Задаче 1 (пункт 2) определитель матрицы перехода отрицателен: ![]() , следовательно, базисы
, следовательно, базисы ![]() задают разную ориентацию трёхмерного пространства. С этим понятием можно ознакомиться в статье о векторном произведении векторов, ну а сейчас пришло время вернуться в основное русло урока:
задают разную ориентацию трёхмерного пространства. С этим понятием можно ознакомиться в статье о векторном произведении векторов, ну а сейчас пришло время вернуться в основное русло урока:
Преобразование прямоугольных систем координат
На практике наиболее часто приходится осуществлять переход от одной правой декартовой системы координат ![]() к другой правой декартовой системе
к другой правой декартовой системе ![]() , и в этом случае общие формулы преобразования координат принимают следующий вид:
, и в этом случае общие формулы преобразования координат принимают следующий вид:
![]() , где
, где ![]() – угол между первыми координатными векторами (не важно, положительный или отрицательный).
– угол между первыми координатными векторами (не важно, положительный или отрицательный).
Данные формулы, в частности используются в ходе приведения уравнения линии 2-го порядка к каноническому виду. И, несмотря на то, что они выражают старые координаты ![]() точки
точки ![]() через новые
через новые ![]() , равенства называют формулами перехода от старой системы координат к новой. Объяснение просто: если в какое-либо уравнение вместо «икса» и «игрека» подставить правые части этих равенств, то, собственно, именно такой переход и будет осуществлён.
, равенства называют формулами перехода от старой системы координат к новой. Объяснение просто: если в какое-либо уравнение вместо «икса» и «игрека» подставить правые части этих равенств, то, собственно, именно такой переход и будет осуществлён.
В том случае если новая система координат построена на тех же базисных векторах: ![]() , то речь идёт лишь о параллельном переносе начала координат, и формулы донельзя упрощаются:
, то речь идёт лишь о параллельном переносе начала координат, и формулы донельзя упрощаются:
![]()
Пусть, например, ![]() – новое начало:
– новое начало:
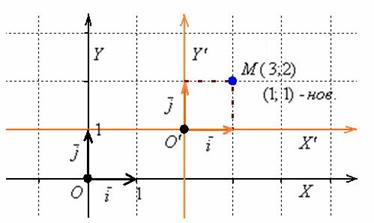
Тогда старые координаты ![]() точки
точки ![]() легко получить из новых:
легко получить из новых: ![]() ,
,
а новые – из старых: ![]()
Второй частный случай – это поворот осей с сохранением начала координат:
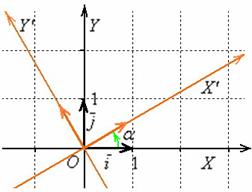
Так как новое начало координат ![]() совпадает со старым, то в формулах преобразования координат исчезают свободные члены:
совпадает со старым, то в формулах преобразования координат исчезают свободные члены:
![]()
Для самостоятельного решения:
Задача 2
Прямоугольная декартова система координат ![]() получена из системы
получена из системы ![]() поворотом на угол
поворотом на угол ![]() .
.
1) С помощью матричного исчисления вывести формулы, выражающие новые координаты ![]() точки
точки ![]() через её старые координаты
через её старые координаты ![]() .
.
2) Найти новые координаты точки ![]() , если известно, что угол поворота
, если известно, что угол поворота ![]() .
.
На чертеже выше изображен именно этот легендарный угол, с синуса и косинуса которого начиналось наше знакомство с тригонометрией. Впрочем, если что – тригонометрические таблицы рядом.
Краткое решение и ответ в конце урока.
В общем случае правая прямоугольная система координат ![]() получается из системы
получается из системы ![]() в два шага:
в два шага:
1) поворотом координатных осей;
2) параллельным переносом начала координат.
Ну, или в другом порядке.
Следует отметить, что для двух левых декартовых систем работают те же самые формулы
![]()
Но вот если одна из прямоугольных систем левая, а другая правая, то в двух местах следует поменять знаки:
![]()
Кстати, здесь уже нельзя рассуждать о «чистом повороте» координатных осей, поскольку с помощью него невозможно «совместить двух Тузиков». И как раз одна система координат получается из другой в том числе с помощью зеркальной симметрии.
Аналогичные формулы преобразования аффинных систем координат имеют место быть в трёхмерном пространстве:
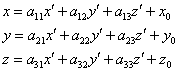 , где:
, где:
где ![]() – координаты точки
– координаты точки ![]() в аффинной системе
в аффинной системе ![]() ;
;
![]() – её координаты в системе
– её координаты в системе ![]() ;
;
![]() – координаты начала
– координаты начала ![]() в системе
в системе ![]() .
.
Грубо говоря, здесь прибавилась одна координата и принципиальная схема рассуждений не изменилась. Но разнообразия (тех же поворотов), стало, безусловно, больше.
И, разумеется, рассмотренный математический аппарат работает для векторов произвольной природы, в том числе векторов бОльшей размерности.
Любите векторы, и векторы полюбят вас!
Решения и ответы:
Задача 1. Решение:
1) Матричное уравнение ![]() , где
, где 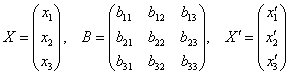 позволяет найти координаты вектора
позволяет найти координаты вектора ![]() в базисе
в базисе ![]() , если известны его координаты в базисе
, если известны его координаты в базисе ![]() . Матричное уравнение
. Матричное уравнение ![]() соотносит координаты в другом порядке
соотносит координаты в другом порядке
2) Запишем матрицу 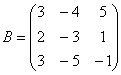 . Координаты вектора
. Координаты вектора ![]() в базисе
в базисе ![]() найдём с помощью матричного уравнения
найдём с помощью матричного уравнения ![]() .
.
Обратную матрицу найдем по формуле:
![]() , где
, где ![]() – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы ![]() .
.
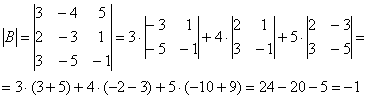
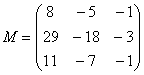 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы ![]() .
.
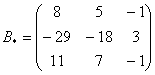 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
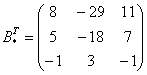 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Таким образом:
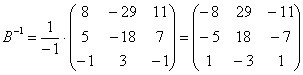
В результате:
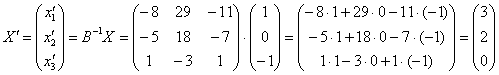
Ответ: ![]()
Примечание: на самом деле такую задачу мы уже решали на уроке о линейной независимости и базисах (см. Примеры 8, 9), но недостаток тех решений состоит в том, что метод Крамера позволяет найти новые координаты лишь отдельно взятого вектора.
Задача 2. Решение:
1) Запишем формулы в матричной форме:
![]()
![]()
Выразим новые координаты через старые: ![]() .
.
Обратную матрицу найдем по формуле:
![]() , где
, где ![]() – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы ![]() .
.
![]()
![]() – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы ![]() .
.
![]() – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
![]() – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Таким образом:
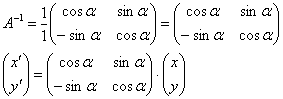
Осуществляя матричное умножение, получаем искомые формулы:
![]()
2) Поскольку угол поворота составляет ![]() , то формулы принимают вид:
, то формулы принимают вид:
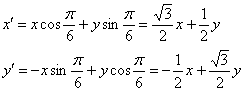
Вычислим координаты точки ![]() в новой системе координат:
в новой системе координат:
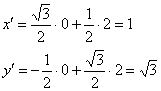
Ответ: а) ![]() , б)
, б) ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright