


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Скалярное произведение векторов
Продолжаем разбираться с векторами. На первом уроке Векторы для чайников мы рассмотрели понятие вектора, действия с векторами, координаты вектора и простейшие задачи с векторами. Но было бы наивным думать, что математики не придумают что-нибудь ещё :) И посему далее по курсу скалярное произведение векторов, векторное произведение векторов и смешанное произведение векторов.
Начнём с действия, которое нам известно ещё с детства нет, не то :). В данной статье я разберу все или почти все задачи на скалярное произведение, которые встречаются как в школе, так и в курсе высшей математики. Если вы хотите сразу посмотреть что-то конкретное, то воспользуйтесь оглавлением, ибо урок недетский. Чайникам же рекомендую изучать всё по порядку, ангем forever:
- Понятие и определение скалярного произведения
- Угол между векторами и значение скалярного произведения
- Скалярный квадрат вектора
- Свойства скалярного произведения
- Угол между векторами через скалярное произведение
- Скалярное произведение в координатах
- Проверка векторов на ортогональность с помощью скалярного произведения
- Скалярное произведение в координатах, если векторы заданы суммами векторов
- Формула косинуса угла между векторами, которые заданы координатами
- Проекция вектора на вектор
- Проекции вектора на координатные оси. Направляющие косинусы вектора
Приоткроем же, наконец, дверь и увлечённо посмотрим, что происходит, когда два вектора встречают друг друга….
Определение скалярного произведения векторов.
Свойства скалярного произведения. Типовые задачи
Понятие и определение скалярного произведения
Сначала про угол между векторами. Думаю, всем интуитивно понятно, что такое угол между векторами, но на всякий случай чуть подробнее. Рассмотрим свободные ненулевые векторы ![]() и
и ![]() . Если отложить данные векторы от произвольной точки
. Если отложить данные векторы от произвольной точки ![]() , то получится картинка, которую многие уже представили мысленно:
, то получится картинка, которую многие уже представили мысленно:
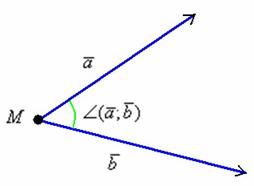
Признаюсь, здесь я обрисовал ситуацию только на уровне понимания. Если необходимо строгое определение угла между векторами, пожалуйста, обратитесь к учебнику, для практических же задач оно нам, в принципе, ни к чему. Также ЗДЕСЬ И ДАЛЕЕ я буду местами игнорировать нулевые векторы ввиду их малой практической значимости. Оговорку сделал специально для продвинутых посетителей сайта, которые могут меня упрекнуть в теоретической неполноте некоторых последующих утверждений.
Угол между векторами ![]() может принимать значения от 0 до 180 градусов (от 0 до
может принимать значения от 0 до 180 градусов (от 0 до ![]() радиан) включительно. Аналитически данный факт записывается в виде двойного неравенства:
радиан) включительно. Аналитически данный факт записывается в виде двойного неравенства: ![]() либо
либо ![]() (в радианах).
(в радианах).
В литературе значок угла ![]() часто пропускают и пишут просто
часто пропускают и пишут просто ![]() .
.
Определение: скалярным произведением двух векторов ![]() и
и ![]() называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними:
называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними:
![]()
Вот это вот уже вполне строгое определение.
Акцентируем внимание на существенной информации:
Обозначение: скалярное произведение обозначается через ![]() или просто
или просто ![]() .
.
Результат операции является ЧИСЛОМ: Умножается вектор на вектор, а получается число. Действительно, если длины векторов ![]() – это числа, косинус угла – число, то их произведение
– это числа, косинус угла – число, то их произведение ![]() тоже будет числом.
тоже будет числом.
Сразу пара разминочных примеров:
Пример 1
Найти скалярное произведение векторов ![]() и
и ![]() , если
, если ![]()
Решение: используем формулу ![]() . В данном случае:
. В данном случае:
![]()
Ответ: ![]()
Значения косинуса можно найти в тригонометрической таблице. Рекомендую её распечатать – потребуется практически во всех разделах вышки и потребуется много раз.
Чисто с математической точки зрения скалярное произведение безразмерно, то есть результат, в данном случае ![]() , просто число и всё. С точки же зрения задач физики скалярное произведение всегда имеет определенный физический смысл, то есть после результата нужно указать ту или иную физическую единицу. Канонический пример по вычислению работы силы можно найти в любом учебнике (формула в точности представляет собой скалярное произведение). Работа силы измеряется в Джоулях, поэтому, и ответ запишется вполне конкретно, например,
, просто число и всё. С точки же зрения задач физики скалярное произведение всегда имеет определенный физический смысл, то есть после результата нужно указать ту или иную физическую единицу. Канонический пример по вычислению работы силы можно найти в любом учебнике (формула в точности представляет собой скалярное произведение). Работа силы измеряется в Джоулях, поэтому, и ответ запишется вполне конкретно, например, ![]() .
.
Пример 2
Найти ![]() , если
, если ![]() , а угол между векторами равен
, а угол между векторами равен ![]() .
.
Это пример для самостоятельного решения, ответ в конце урока.
Угол между векторами и значение скалярного произведения
В Примере 1 скалярное произведение получилось положительным, а в Примере 2 – отрицательным. Выясним, от чего зависит знак скалярного произведения. Смотрим на нашу формулу: ![]() . Длины ненулевых векторов всегда положительны:
. Длины ненулевых векторов всегда положительны: ![]() , поэтому знак может зависеть только от значения косинуса.
, поэтому знак может зависеть только от значения косинуса.
Примечание: для более качественного понимания нижеприведенной информации лучше изучить график косинуса в методичке Графики и свойства функции. Посмотрите, как ведёт себя косинус на отрезке ![]() .
.
Как уже отмечалось, угол между векторами может изменяться в пределах ![]() , и при этом возможны следующие случаи:
, и при этом возможны следующие случаи:
1) Если угол между векторами острый: ![]() (от 0 до 90 градусов), то
(от 0 до 90 градусов), то ![]() , и скалярное произведение будет положительным:
, и скалярное произведение будет положительным: ![]() . Особый случай: если векторы сонаправлены, то угол между ними считается нулевым
. Особый случай: если векторы сонаправлены, то угол между ними считается нулевым ![]() , и скалярное произведение также будет положительным. Поскольку
, и скалярное произведение также будет положительным. Поскольку ![]() , то формула упрощается:
, то формула упрощается: ![]() .
.
2) Если угол между векторами тупой: ![]() (от 90 до 180 градусов), то
(от 90 до 180 градусов), то ![]() , и, соответственно, скалярное произведение отрицательно:
, и, соответственно, скалярное произведение отрицательно: ![]() . Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым:
. Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым: ![]() (180 градусов). Скалярное произведение тоже отрицательно, так как
(180 градусов). Скалярное произведение тоже отрицательно, так как ![]()
Справедливы и обратные утверждения:
1) Если ![]() , то угол между данными векторами острый. Как вариант, векторы сонаправлены.
, то угол между данными векторами острый. Как вариант, векторы сонаправлены.
2) Если ![]() , то угол между данными векторами тупой. Как вариант, векторы направлены противоположно.
, то угол между данными векторами тупой. Как вариант, векторы направлены противоположно.
Но особый интерес представляет третий случай:
3) Если угол между векторами прямой: ![]() (90 градусов), то
(90 градусов), то ![]() и скалярное произведение равно нулю:
и скалярное произведение равно нулю: ![]() . Обратное тоже верно: если
. Обратное тоже верно: если ![]() , то
, то ![]() . Компактно утверждение формулируется так: Скалярное произведение двух векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись:
. Компактно утверждение формулируется так: Скалярное произведение двух векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись: ![]()
! Примечание: повторим основы математической логики: двусторонний значок логического следствия ![]() обычно читают «тогда и только тогда», «в том и только в том случае». Как видите, стрелки направлены в обе стороны – «из этого следует это, и обратно – из того, следует это». В чём, кстати, отличие от одностороннего значка следования
обычно читают «тогда и только тогда», «в том и только в том случае». Как видите, стрелки направлены в обе стороны – «из этого следует это, и обратно – из того, следует это». В чём, кстати, отличие от одностороннего значка следования ![]() ? Значок
? Значок ![]() утверждает, только то, что «из этого следует это», и не факт, что обратное справедливо. Например:
утверждает, только то, что «из этого следует это», и не факт, что обратное справедливо. Например: ![]() , но не каждый зверь является пантерой, поэтому в данном случае нельзя использовать значок
, но не каждый зверь является пантерой, поэтому в данном случае нельзя использовать значок ![]() . В то же время, вместо значка
. В то же время, вместо значка ![]() можно использовать односторонний значок. Например, решая задачу, мы выяснили, что
можно использовать односторонний значок. Например, решая задачу, мы выяснили, что ![]() и сделали вывод, что векторы ортогональны:
и сделали вывод, что векторы ортогональны: ![]() – такая запись будет корректной, и даже более уместной, чем
– такая запись будет корректной, и даже более уместной, чем ![]() .
.
Третий случай имеет большую практическую значимость, поскольку позволяет проверить, ортогональны векторы или нет. Данную задачу мы решим во втором разделе урока.
Скалярный квадрат вектора
Вернёмся к ситуации, когда два вектора сонаправлены. В этом случае угол между ними равен нулю, ![]() , и формула скалярного произведения принимает вид:
, и формула скалярного произведения принимает вид: ![]() .
.
А что будет, если вектор ![]() умножить на самого себя? Понятно, что вектор сонаправлен сам с собой, поэтому пользуемся вышеуказанной упрощенной формулой:
умножить на самого себя? Понятно, что вектор сонаправлен сам с собой, поэтому пользуемся вышеуказанной упрощенной формулой:
![]()
Или: ![]()
Число ![]() называется скалярным квадратом вектора
называется скалярным квадратом вектора ![]() , и обозначатся как
, и обозначатся как ![]() .
.
Таким образом, скалярный квадрат вектора ![]() равен квадрату длины данного вектора:
равен квадрату длины данного вектора:
![]()
Из данного равенства можно получить формулу для вычисления длины вектора:
![]()
Пока она кажется малопонятной, но задачи урока всё расставят на свои места. Для решения задач нам также потребуются
свойства скалярного произведения
Для произвольных векторов ![]() и любого числа
и любого числа ![]() справедливы следующие свойства:
справедливы следующие свойства:
1) ![]() – переместительный или коммутативный закон скалярного произведения.
– переместительный или коммутативный закон скалярного произведения.
2) ![]() – распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
– распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
3) ![]() – сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.
– сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.
Зачастую, всевозможные свойства (которые ещё и доказывать надо!) воспринимаются студентами как ненужный хлам, который лишь необходимо вызубрить и сразу после экзамена благополучно забыть. Казалось бы, чего тут важного, все и так с первого класса знают, что от перестановки множителей произведение не меняется: ![]() . Должен предостеречь, в высшей математике с подобным подходом легко наломать дров. Так, например, переместительное свойство не является справедливым для алгебраических матриц. Неверно оно и для векторного произведения векторов. Поэтому, в любые свойства, которые вам встретятся в курсе высшей математики, как минимум, лучше вникать, чтобы понять, что можно делать, а чего нельзя.
. Должен предостеречь, в высшей математике с подобным подходом легко наломать дров. Так, например, переместительное свойство не является справедливым для алгебраических матриц. Неверно оно и для векторного произведения векторов. Поэтому, в любые свойства, которые вам встретятся в курсе высшей математики, как минимум, лучше вникать, чтобы понять, что можно делать, а чего нельзя.
Пример 3
Найти скалярное произведение векторов ![]() и
и ![]() , если известно, что
, если известно, что ![]() .
.
Решение: сначала проясним ситуацию с вектором ![]() . Что это вообще такое? Сумма векторов
. Что это вообще такое? Сумма векторов ![]() и
и ![]() представляет собой вполне определенный вектор, который и обозначен через
представляет собой вполне определенный вектор, который и обозначен через ![]() . Геометрическую интерпретацию действий с векторами можно найти в статье Векторы для чайников. Та же история с вектором
. Геометрическую интерпретацию действий с векторами можно найти в статье Векторы для чайников. Та же история с вектором ![]() – это сумма векторов
– это сумма векторов ![]() и
и ![]() .
.
Итак, по условию требуется найти скалярное произведение ![]() . По идее, нужно применить рабочую формулу
. По идее, нужно применить рабочую формулу ![]() , но беда в том, что нам неизвестны длины векторов
, но беда в том, что нам неизвестны длины векторов ![]() и угол между ними. Зато в условии даны аналогичные параметры для векторов
и угол между ними. Зато в условии даны аналогичные параметры для векторов ![]() , поэтому мы пойдём другим путём:
, поэтому мы пойдём другим путём:
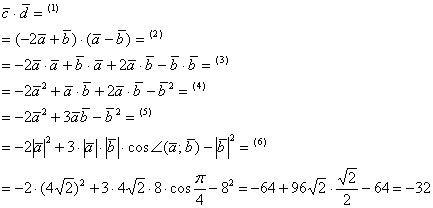
(1) Подставляем выражения векторов ![]() .
.
(2) Раскрываем скобки по правилу умножения многочленов, пошлую скороговорку можно найти в статье Комплексные числа или Интегрирование дробно-рациональной функции. Повторяться уж не буду =) Кстати, раскрыть скобки нам позволяет дистрибутивное свойство скалярного произведения. Имеем право.
(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов: ![]() . Во втором слагаемом используем перестановочность скалярного произведения:
. Во втором слагаемом используем перестановочность скалярного произведения: ![]() .
.
(4) Приводим подобные слагаемые: ![]() .
.
(5) В первом слагаемом используем формулу скалярного квадрата ![]() , о которой не так давно упоминалось. В последнем слагаемом, соответственно, работает та же штука:
, о которой не так давно упоминалось. В последнем слагаемом, соответственно, работает та же штука: ![]() . Второе слагаемое раскладываем по стандартной формуле
. Второе слагаемое раскладываем по стандартной формуле ![]() .
.
(6) Подставляем данные условия ![]() , и ВНИМАТЕЛЬНО проводим окончательные вычисления.
, и ВНИМАТЕЛЬНО проводим окончательные вычисления.
Ответ: ![]()
Отрицательное значение скалярного произведения констатирует тот факт, что угол между векторами ![]() является тупым.
является тупым.
Задача типовая, вот пример для самостоятельного решения:
Пример 4
Найти скалярное произведение векторов ![]() и
и ![]() , если известно, что
, если известно, что ![]() .
.
Краткое решение и ответ в конце урока.
Теперь ещё одно распространённое задание, как раз на новую формулу длины вектора ![]() . Обозначения тут будут немного совпадать, поэтому для ясности я перепишу её с другой буквой:
. Обозначения тут будут немного совпадать, поэтому для ясности я перепишу её с другой буквой: ![]()
Пример 5
Найти длину вектора ![]() , если
, если ![]() .
.
Решение будет следующим:
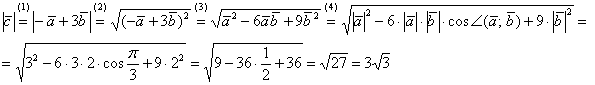
(1) Поставляем выражение вектора ![]() .
.
(2) Используем формулу длины: ![]() , при этом в качестве вектора «вэ» у нас выступает целое выражение
, при этом в качестве вектора «вэ» у нас выступает целое выражение ![]() .
.
(3) Используем школьную формулу квадрата суммы ![]() . Обратите внимание, как она здесь любопытно работает:
. Обратите внимание, как она здесь любопытно работает: ![]() – фактически это квадрат разности, и, по сути, так оно и есть. Желающие могут переставить векторы местами:
– фактически это квадрат разности, и, по сути, так оно и есть. Желающие могут переставить векторы местами: ![]() – получилось то же самое с точностью до перестановки слагаемых.
– получилось то же самое с точностью до перестановки слагаемых.
(4) Дальнейшее уже знакомо из двух предыдущих задач.
Ответ: ![]()
Коль скоро речь идёт о длине, не забываем указать размерность – «единицы».
Пример 6
Найти длину вектора ![]() , если
, если ![]() .
.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Угол между векторами
Продолжаем выжимать полезные вещи из скалярного произведения. Снова посмотрим на нашу формулу ![]() . По правилу пропорции сбросим длины векторов в знаменатель левой части:
. По правилу пропорции сбросим длины векторов в знаменатель левой части:
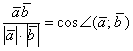
А части поменяем местами:
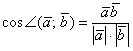
В чём смысл данной формулы? Если известны длины двух векторов и их скалярное произведение, то можно вычислить косинус угла между данными векторами, а, следовательно, и сам угол.
Скалярное произведение ![]() – это число? Число. Длины векторов
– это число? Число. Длины векторов ![]() – числа? Числа. Значит, дробь
– числа? Числа. Значит, дробь ![]() тоже является некоторым числом
тоже является некоторым числом ![]() . А если известен косинус угла:
. А если известен косинус угла: ![]() , то с помощью обратной функции легко найти и сам угол:
, то с помощью обратной функции легко найти и сам угол: ![]() .
.
Пример 7
Найти угол между векторами ![]() и
и ![]() , если известно, что
, если известно, что ![]() .
.
Решение: используем формулу:
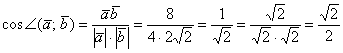
На заключительном этапе вычислений использован технический приём – устранение иррациональности в знаменателе. В целях устранения иррациональности я домножил числитель и знаменатель на ![]() .
.
Итак, если ![]() , то:
, то:
![]()
Значения обратных тригонометрических функций можно находить по тригонометрической таблице. Хотя случается это редко. В задачах аналитической геометрии значительно чаще появляется какой-нибудь неповоротливый медведь вроде ![]() , и значение угла приходится находить приближенно, используя калькулятор. Собственно, такую картину мы ещё неоднократно увидим.
, и значение угла приходится находить приближенно, используя калькулятор. Собственно, такую картину мы ещё неоднократно увидим.
Ответ: ![]()
Опять, не забываем указывать размерность – радианы и градусы. Лично я, чтобы заведомо «снять все вопросы», предпочитаю указывать и то, и то (если по условию, конечно, не требуется представить ответ только в радианах или только в градусах).
Теперь вы сможете самостоятельно справиться с более сложным заданием:
Пример 7*
Даны ![]() – длины векторов
– длины векторов ![]() ,
, ![]() и угол между ними
и угол между ними ![]() . Найти угол между векторами
. Найти угол между векторами ![]() ,
, ![]() .
.
Задание даже не столько сложное, сколько многоходовое.
Разберём алгоритм решения:
1) По условию, требуется найти угол между векторами ![]() и
и ![]() , поэтому нужно использовать формулу
, поэтому нужно использовать формулу 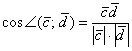 .
.
2) Находим скалярное произведение ![]() (см. Примеры № 3, 4).
(см. Примеры № 3, 4).
3) Находим длину вектора ![]() и длину вектора
и длину вектора ![]() (см. Примеры № 5, 6).
(см. Примеры № 5, 6).
4) Концовка решения совпадает с Примером № 7 – нам известно число ![]() , а значит, легко найти и сам угол:
, а значит, легко найти и сам угол: 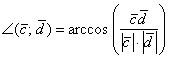
Краткое решение и ответ в конце урока.
Второй раздел урока посвящен тому же скалярному произведению. Координаты. Будет даже проще, чем в первой части.
Скалярное произведение векторов,
заданных координатами в ортонормированном базисе
На уроке Векторы для чайников мы рассматривали два случая: векторы на плоскости и векторы в трехмерном пространстве, при этом «плоские» и «пространственные» формулы были весьма похожи. Для скалярного произведения векторов всё точно так же! Прежде чем продолжать дальше, скажу, что все рассмотренные выше утверждения, теоремы и задачи (первого раздела данной статьи) справедливы как для плоскости, так и для пространства.
Второе важное замечание касается базиса. В данном разделе рассматриваются только ортонормированные базисы плоскости и пространства.
Повествование опять пойдёт параллельно – и для векторов плоскости и для пространственных векторов.
Скалярное произведение в координатах
Скалярное произведение векторов ![]() и
и ![]() , заданных в ортонормированном базисе
, заданных в ортонормированном базисе ![]() , выражается формулой
, выражается формулой ![]()
Скалярное произведение векторов ![]() , заданных в ортонормированном базисе
, заданных в ортонормированном базисе ![]() , выражается формулой
, выражается формулой ![]()
То есть скалярное произведение равно сумме произведений соответствующих координат векторов.
Пример 8
Найти скалярное произведение векторов:
а) ![]() и
и ![]()
б) ![]() и
и ![]() , если даны точки
, если даны точки ![]()
Решение:
а) Здесь даны векторы плоскости. По формуле ![]() :
:
![]()
К слову: скалярное произведение получилось отрицательным, значит, угол между данными векторами является тупым. Пытливые умы могут отложить на плоскости векторы ![]() от одной точки, и убедиться, что это действительно так.
от одной точки, и убедиться, что это действительно так.
б) А тут речь идёт о точках и векторах пространства. Сначала найдём векторы:
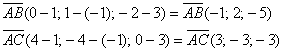
Надеюсь, эта простейшая задача у вас уже отработана.
По формуле ![]() вычислим скалярное произведение:
вычислим скалярное произведение:
![]()
К слову: скалярное произведение положительно, значит, угол между пространственными векторами ![]() является острым.
является острым.
Ответ: ![]()
При некотором опыте скалярное произведение можно приноровиться считать устно.
Проверка векторов на ортогональность с помощью скалярного произведения
Вернёмся к важному случаю, когда векторы являются ортогональными. Напоминаю: векторы ![]() и
и ![]() ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда ![]() . В координатах данный факт запишется следующим образом:
. В координатах данный факт запишется следующим образом:
![]() (для векторов плоскости);
(для векторов плоскости);
![]() (для векторов пространства).
(для векторов пространства).
Пример 9
а) Проверить ортогональность векторов: ![]() и
и ![]()
б) Выяснить, будут ли перпендикулярными отрезки ![]() и
и ![]() , если
, если ![]()
Решение:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение:
![]() , следовательно,
, следовательно, ![]()
б) Здесь речь идёт об обычных отрезках плоскости (в чём сходство и различия вектора и отрезка, я очень подробно разъяснил на первом уроке). Речь идёт об обычных отрезках, а задача всё равно решается через векторы. Найдём векторы:
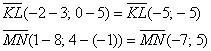
Вычислим их скалярное произведение:
![]() , значит, отрезки
, значит, отрезки ![]() и
и ![]() не перпендикулярны.
не перпендикулярны.
Обратите внимание на два существенных момента:
– В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
– В окончательном выводе «между строк» подразумевается: «если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными». Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках: «значит, отрезки ![]() и
и ![]() не перпендикулярны».
не перпендикулярны».
Ответ: а) ![]() , б) отрезки
, б) отрезки ![]() не перпендикулярны.
не перпендикулярны.
Пример 10
Даны четыре точки пространства ![]() . Выяснить будут ли перпендикулярными следующие прямые:
. Выяснить будут ли перпендикулярными следующие прямые:
а) ![]() ;
;
б) ![]() .
.
Это задача для самостоятельного решения. В условии требуется проверить перпендикулярность прямых. А решается задача снова через векторы по полной аналогии с предыдущим примером. Геометрически тоже всё очевидно – если удастся доказать перпендикулярность векторов, то из этого автоматически будет следовать перпендикулярность соответствующих прямых. Четыре вектора, которые вы найдёте, называют направляющими векторами прямых.
Полное решение и ответ в конце урока.
Мощь аналитической геометрии – в векторах. Так, в рассмотренных примерах, с помощью скалярного произведения можно установить не только ортогональность векторов самих по себе, но и перпендикулярность отрезков, прямых. И это приоткрылась только малая часть красоты предмета.
Завершая разговор об ортогональности, разберу ещё одну небольшую задачу, которая время от времени встречается на практике:
Пример 11
При каком значении ![]() векторы
векторы ![]() будут ортогональны?
будут ортогональны?
Решение: по условию, требуется найти такое значение параметра ![]() , чтобы данные векторы были ортогональны. Два вектора пространства
, чтобы данные векторы были ортогональны. Два вектора пространства ![]() ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда ![]() .
.
Дело за малым, составим уравнение:
![]()
Раскрываем скобки и приводим подобные слагаемые:
![]()
Решаем простейшее линейное уравнение:
![]()
Ответ: при ![]()
В рассмотренной задаче легко выполнить проверку, в исходные векторы ![]() подставляем полученное значение параметра
подставляем полученное значение параметра ![]() :
:
![]()
И находим скалярное произведение:
![]() – да, действительно, при
– да, действительно, при ![]() векторы
векторы ![]() ортогональны, что и требовалось проверить.
ортогональны, что и требовалось проверить.
Пример 12
При каком значении ![]() скалярное произведение векторов
скалярное произведение векторов ![]() будет равно –2?
будет равно –2?
Это простенький пример с векторами плоскости. Для самостоятельного решения.
Немного усложним задачу:
Скалярное произведение в координатах, если векторы заданы суммами векторов
Пример 13
Найти скалярное произведение векторов ![]() , если
, если ![]()
Решение: напрашивается трафаретный путь предыдущего раздела, где мы раскрывали скобки: ![]() . Но зачем? Есть более лаконичное решение:
. Но зачем? Есть более лаконичное решение:
Найдём вектор ![]() :
:
![]()
Найдём вектор ![]() :
:
![]()
Проделаны элементарные действия с векторами, которые рассмотрены в конце урока Векторы для чайников.
Вычислим скалярное произведение:
![]()
Ответ: ![]()
Что и говорить, иметь дело с координатами значительно приятнее.
Пример 14
Найти скалярное произведение векторов ![]() и
и ![]() , если
, если ![]()
Это пример для самостоятельного решения. Здесь можно использовать ассоциативность операции, то есть не считать ![]() , а сразу вынести тройку за пределы скалярного произведения и домножить на неё в последнюю очередь. Решение и ответ в конце урока.
, а сразу вынести тройку за пределы скалярного произведения и домножить на неё в последнюю очередь. Решение и ответ в конце урока.
В заключение параграфа провокационный пример на вычисление длины вектора:
Пример 15
Найти длины векторов ![]() , если
, если ![]()
Решение: снова напрашивается способ предыдущего раздела: ![]() , но существует и другая дорога:
, но существует и другая дорога:
Найдём вектор ![]() :
:
![]()
И его длину по тривиальной формуле ![]() :
:
![]()
Скалярное произведение здесь вообще не при делах!
Как не при делах оно и при вычислении длины вектора ![]() :
:
![]() Стоп. А не воспользоваться ли очевидным свойством длины вектора? Что можно сказать о длине вектора
Стоп. А не воспользоваться ли очевидным свойством длины вектора? Что можно сказать о длине вектора ![]() ? Данный вектор длиннее вектора
? Данный вектор длиннее вектора ![]() в 5 раз. Направление противоположно, но это не играет роли, ведь разговор о длине. Очевидно, что длина вектора
в 5 раз. Направление противоположно, но это не играет роли, ведь разговор о длине. Очевидно, что длина вектора ![]() равна произведению модуля числа
равна произведению модуля числа ![]() на длину вектора
на длину вектора ![]() :
:
![]() – знак модуля «съедает» возможный минус числа
– знак модуля «съедает» возможный минус числа ![]() .
.
Таким образом:
![]()
Ответ: ![]()
Формула косинуса угла между векторами, которые заданы координатами
Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса угла между векторами ![]() выразить через координаты векторов
выразить через координаты векторов ![]() :
:
Косинус угла между векторами плоскости ![]() и
и ![]() , заданными в ортонормированном базисе
, заданными в ортонормированном базисе ![]() , выражается формулой:
, выражается формулой:
![]() .
.
Косинус угла между векторами пространства ![]() , заданными в ортонормированном базисе
, заданными в ортонормированном базисе ![]() , выражается формулой:
, выражается формулой:
![]()
Пример 16
Даны вершины треугольника ![]() . Найти
. Найти ![]() (угол при вершине
(угол при вершине ![]() ).
).
Решение: по условию, чертёж выполнять не требуется, но науки ради:
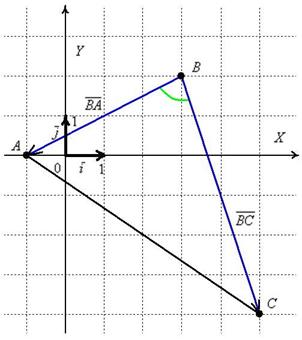
Требуемый угол ![]() помечен зелёной дугой. Сразу вспоминаем школьное обозначение угла:
помечен зелёной дугой. Сразу вспоминаем школьное обозначение угла: ![]() – особое внимание на среднюю букву
– особое внимание на среднюю букву ![]() – это и есть нужная нам вершина угла. Для краткости можно было также записать просто
– это и есть нужная нам вершина угла. Для краткости можно было также записать просто ![]() .
.
Из чертежа совершенно очевидно, что угол ![]() треугольника совпадает с углом между векторами
треугольника совпадает с углом между векторами ![]() и
и ![]() , иными словами:
, иными словами: ![]() .
.
Проведённый анализ желательно научиться выполнять мысленно.
Найдём векторы:
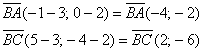
Вычислим скалярное произведение:
![]()
И длины векторов:
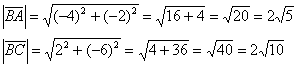
Косинус угла:
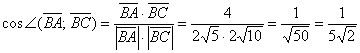
Именно такой порядок выполнения задания рекомендую чайникам. Более подготовленные читатели могут записывать вычисления «одной строкой»:
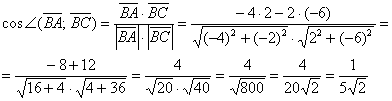
Вот и пример «плохого» значения косинуса. Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
![]()
Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки угол также можно измерить и транспортиром. Не повредите покрытие монитора =)
Ответ: ![]()
В ответе не забываем, что спрашивалось про угол треугольника (а не про угол между векторами), не забываем указать точный ответ: ![]() и приближенное значение угла:
и приближенное значение угла: ![]() , найденное с помощью калькулятора.
, найденное с помощью калькулятора.
Те, кто получил удовольствие от процесса, могут вычислить углы ![]() , и убедиться в справедливости канонического равенства
, и убедиться в справедливости канонического равенства ![]()
Пример 17
В пространстве задан треугольник координатами своих вершин ![]() . Найти угол между сторонами
. Найти угол между сторонами ![]() и
и ![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока
Небольшой заключительный раздел будет посвящен проекциям, в которых тоже «замешано» скалярное произведение:
Проекции
Проекция вектора на вектор
Вектор можно проецировать под разными углами, но чаще всего (и по умолчанию) под проекцией подразумевают ортогональную проекцию. Рассмотрим векторы ![]() и
и ![]() :
:
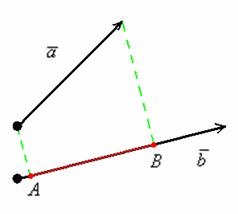
Спроецируем вектор ![]() на вектор
на вектор ![]() , для этого из начала и конца вектора
, для этого из начала и конца вектора ![]() опустим перпендикуляры на вектор
опустим перпендикуляры на вектор ![]() (зелёные пунктирные линии). Представьте, что на вектор
(зелёные пунктирные линии). Представьте, что на вектор ![]() перпендикулярно падают лучи света. Тогда отрезок
перпендикулярно падают лучи света. Тогда отрезок ![]() (красная линия) будет «тенью» вектора
(красная линия) будет «тенью» вектора ![]() . В данном случае проекцией вектора
. В данном случае проекцией вектора ![]() на вектор
на вектор ![]() является ДЛИНА отрезка
является ДЛИНА отрезка ![]() . То есть ПРОЕКЦИЯ – ЭТО ЧИСЛО.
. То есть ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Данное ЧИСЛО обозначается следующим образом: ![]() , «большим вектором» обозначают вектор КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НА который проецируют.
, «большим вектором» обозначают вектор КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись ![]() читается так: «проекция вектора «а» на вектор «бэ»».
читается так: «проекция вектора «а» на вектор «бэ»».
Что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на прямую, содержащую вектор «бэ».
Если угол между векторами ![]() острый (как на рисунке), то
острый (как на рисунке), то ![]()
Если векторы ![]() ортогональны, то
ортогональны, то ![]() (проекцией является точка, размеры которой считаются нулевыми).
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами ![]() тупой (на рисунке мысленно переставьте стрелочку вектора
тупой (на рисунке мысленно переставьте стрелочку вектора ![]() ), то
), то ![]() (та же длина, но взятая со знаком минус).
(та же длина, но взятая со знаком минус).
Отложим данные векторы от одной точки:
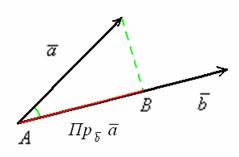
Очевидно, что при перемещении вектора его проекция не меняется
Вспомним школу. Рассмотрим прямоугольный треугольник. Косинусом острого угла называется отношение прилежащего катета к гипотенузе. В данном случае:
![]()
С другой стороны, у нас уже получена формула косинуса угла между векторами:
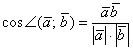
Таким образом:
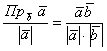
Сокращаем знаменатели обеих частей на ![]() и получаем формулу для вычисления проекции:
и получаем формулу для вычисления проекции:
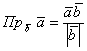
Формула выведена, распишем её в координатах:
Если векторы плоскости ![]() и
и ![]() , заданы в ортонормированном базисе
, заданы в ортонормированном базисе ![]() , то проекция вектора
, то проекция вектора ![]() на вектор
на вектор ![]() выражается формулой:
выражается формулой:
![]() .
.
Если векторы пространства ![]() , заданы в ортонормированном базисе
, заданы в ортонормированном базисе ![]() , то проекция вектора
, то проекция вектора ![]() на вектор
на вектор ![]() выражается формулой:
выражается формулой:
![]()
Пример 18
Найти проекцию вектора ![]() на вектор
на вектор ![]()
Решение в одну строчку:
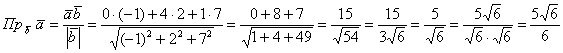
Ответ: ![]()
Проекция – это ДЛИНА, поэтому обязательно указываем размерность. Длина, конечно, своеобразная, в случае тупизны угла между векторами к ней добавляется знак «минус».
В задачах приходится находить не только проекцию вектора на вектор, но и проекцию отрезка на отрезок, отрезка на прямую и т. д. Но, так или иначе, в решении используются векторы!
Пример 19
Треугольник задан своими вершинами ![]() . Найти:
. Найти:
а) проекцию стороны ![]() на сторону
на сторону ![]() ;
;
б) проекцию стороны ![]() на сторону
на сторону ![]() .
.
Это задача для самостоятельного решения. Решение и ответ в конце урока.
Выясним геометрический смысл координат векторов в ортонормированном базисе:
Проекции вектора на координатные оси.
Направляющие косинусы вектора
Рассмотрим вектор плоскости ![]() , заданный своими координатами в ортонормированном базисе
, заданный своими координатами в ортонормированном базисе ![]() . Для удобства я отложу его от начала координат:
. Для удобства я отложу его от начала координат:
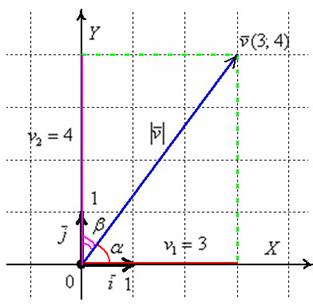
Проекцией вектора ![]() на координатную ось
на координатную ось ![]() является в точности его первая координата:
является в точности его первая координата: ![]() (красная черта). Обозначим через
(красная черта). Обозначим через ![]() угол между вектором
угол между вектором ![]() и координатным вектором
и координатным вектором ![]() :
: ![]() (красная дуга). Тогда:
(красная дуга). Тогда:
![]() (определение косинуса в прямоугольном треугольнике недавно упоминалось).
(определение косинуса в прямоугольном треугольнике недавно упоминалось).
Аналогично со второй координатой: проекцией вектора ![]() на координатную ось
на координатную ось ![]() является его вторая координата:
является его вторая координата: ![]() (малиновая черта). Обозначим через
(малиновая черта). Обозначим через ![]() угол между вектором
угол между вектором ![]() и координатным вектором
и координатным вектором ![]() :
: ![]() (двойная малиновая дуга). Тогда:
(двойная малиновая дуга). Тогда:
![]()
Косинусы ![]() называются направляющими косинусами вектора. Причём, для любого ненулевого вектора справедливо равенство
называются направляющими косинусами вектора. Причём, для любого ненулевого вектора справедливо равенство ![]() . Проверим его справедливость для рассматриваемого вектора:
. Проверим его справедливость для рассматриваемого вектора:
![]() , что и требовалось проверить.
, что и требовалось проверить.
Заметьте, что приведённые выше выкладки не изменятся, если вектор ![]() отложить от любой другой точки плоскости.
отложить от любой другой точки плоскости.
Итак, координаты вектора в ортонормированном базисе – это его проекции на направления соответствующих координатных векторов (координатные оси).
Направляющие косинусы ненулевого вектора ![]() , заданного в ортонормированном базисе
, заданного в ортонормированном базисе ![]() , выражаются формулами
, выражаются формулами ![]() , а сами координаты вектора можно выразить через его длину и данные косинусы:
, а сами координаты вектора можно выразить через его длину и данные косинусы: ![]() , то есть:
, то есть: ![]() .
.
Кроме того, вектор с координатами из соответствующих направляющих косинусов:
– коллинеарен исходному вектору «вэ»;
– его длина равна единице (так называемый единичный вектор).
С пространственными векторами, заданными в ортонормированном базисе ![]() , разборки точно такие же. Рассмотрим произвольный ненулевой вектор
, разборки точно такие же. Рассмотрим произвольный ненулевой вектор ![]() . Его координаты представляют собой проекции вектора на оси
. Его координаты представляют собой проекции вектора на оси ![]() соответственно. Обозначим углы данного вектора с ортами через:
соответственно. Обозначим углы данного вектора с ортами через: ![]() . Тогда направляющие косинусы вектора выражаются формулами:
. Тогда направляющие косинусы вектора выражаются формулами: ![]() , и справедливым является равенство
, и справедливым является равенство ![]() .
.
В практических задачах чаще всего требуется найти направляющие косинусы вектора, заключительный пример урока:
Пример 20
Найти направляющие косинусы векторов:
а) ![]() , проверить, что
, проверить, что ![]() ;
;
б) ![]() , проверить, что
, проверить, что ![]() .
.
Простая задача для самостоятельного решения. Фактически, она состоит в том, чтобы найти длину векторов и составить эти самые направляющие косинусы. Однако не забывайте, что вместе с направляющими косинусами нам автоматически становятся известными единичные векторы, которые коллинеарны векторам «а» и «бэ». К слову, практическая задача на нахождения единичного вектора рассмотрена в Примере № 5 урока Уравнение плоскости. Ну а здесь решение и ответ совсем близко.
После изучения данного урока, у вас уже весьма приличная подготовка по аналитической геометрии. Чтобы паззл сложился окончательно, читайте статьи Линейная (не) зависимость векторов. Базис векторов и Векторное и смешанное произведение векторов.
Любите векторы, и векторы полюбят вас!
Решения и ответы:
Пример 2. Решение:
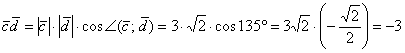
Ответ: ![]()
Пример 4. Решение:
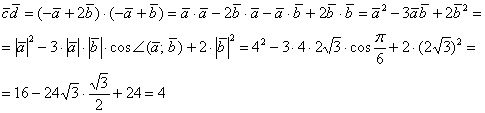
Ответ: ![]()
Пример 6. Решение:
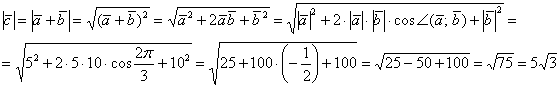
Ответ: ![]()
Пример 7*. Решение: используем формулу 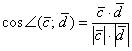 .
.
Найдём скалярное произведение:
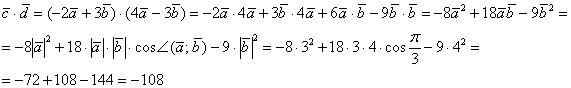
Найдём длину вектора ![]() :
:
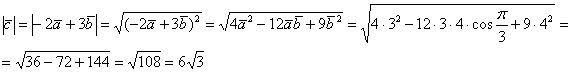
Найдём длину вектора ![]() :
:
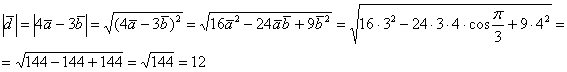
Таким образом:
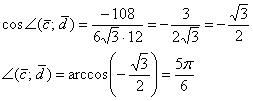
Ответ: ![]()
Пример 10. Решение:
а) Найдем векторы:
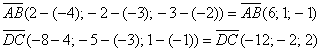
Вычислим скалярное произведение:
![]() , значит, прямые
, значит, прямые ![]() не перпендикулярны.
не перпендикулярны.
б) Найдем векторы:
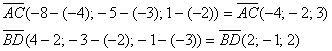
Вычислим скалярное произведение:
![]() , значит, прямые
, значит, прямые ![]() перпендикулярны.
перпендикулярны.
Ответ: а) прямые ![]() не перпендикулярны, б)
не перпендикулярны, б) ![]()
Пример 12. Решение: составим и решим уравнение:
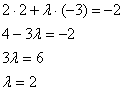
Ответ: при ![]()
Пример 14. Решение:
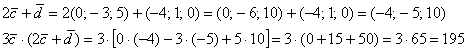
Ответ: ![]()
Пример 17. Решение: найдём векторы ![]()
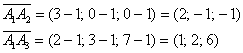
Вычислим косинус угла:
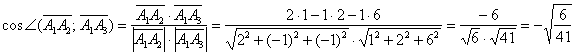
Угол: 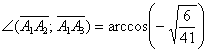
Ответ: 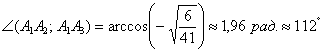
Пример 19. Решение: найдём векторы:
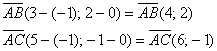
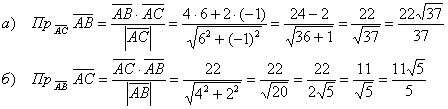
Ответ: ![]()
Пример 20. Решение:
а) Найдём длину вектора: ![]() .
.
Направляющие косинусы: ![]() .
.
Проверка: 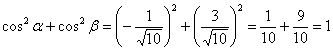 , что и требовалось проверить.
, что и требовалось проверить.
б) Найдём длину вектора: ![]() .
.
Направляющие косинусы: ![]() .
.
Проверка: 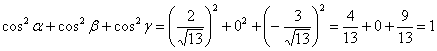 , что и требовалось проверить.
, что и требовалось проверить.
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright