


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Сложные интегралы
Данная статья завершает тему неопределенных интегралов, и в неё включены интегралы, которые я считаю достаточно сложными. Урок создан по неоднократным просьбам посетителей, которые высказывали пожелания, чтобы на сайте были разобраны и более трудные примеры.
Предполагается, что читатель сего текста хорошо подготовлен и умеет применять основные приемы интегрирования. Чайникам и людям, которые не очень уверенно разбираются в интегралах, следует обратиться к самому первому уроку – Неопределенный интеграл. Примеры решений, где можно освоить тему практически с нуля. Более опытные студенты могут ознакомиться с приемами и методами интегрирования, которые в моих статьях еще не встречались.
Какие интегралы будут рассмотрены?
Сначала мы рассмотрим интегралы с корнями, для решения которых последовательно используется замена переменной и интегрирование по частям. То есть в одном примере комбинируются сразу два приёма. И даже больше.
Затем мы познакомимся с интересным и оригинальным методом сведения интеграла к самому себе. Данным способом решается не так уж мало интегралов.
Третьим номером программы пойдут интегралы от сложных дробей, которые пролетели мимо кассы в предыдущих статьях.
В-четвертых, будут разобраны дополнительные интегралы от тригонометрических функций. В частности, существуют методы, которые позволяют избежать трудоемкой универсальной тригонометрической подстановки.
И в заключение рассмотрим интеграл от корня из дроби, в числителе и знаменателе которой находятся линейные функции.
Конечно, название урока не совсем точно, будут и не сказать, что сильно сложные интегралы. Тем не менее, крепких орешков предостаточно. Запланировано довольно много примеров, поэтому поехали.
Последовательная замена переменной и интегрирование по частям
Пример 1
Найти неопределенный интеграл
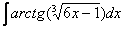
Подынтегральная функция представляет собой арктангенс, под которым находится кубический корень. Первая же мысль, которая приходит в голову – избавиться бы от этого корня. Данный вопрос решается путем замены переменной, сама техника замены специфична, и она подробно рассмотрена на уроке Интегралы от иррациональных функций. Проведем замену:
![]()
После такой замены у нас получится вполне симпатичная вещь: ![]()
Осталось выяснить, во что превратится ![]() . Навешиваем дифференциалы на обе части нашей замены:
. Навешиваем дифференциалы на обе части нашей замены:
![]()
И само собой раскрываем дифференциалы:
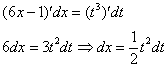
На чистовике решение кратко записывается примерно так:
![]()
Проведем замену:
![]()
![]()
В результате замены получен знакомый тип интеграла, который интегрируется по частям:

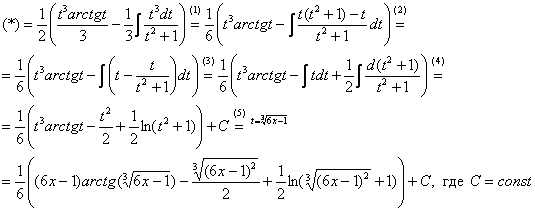
(1) Выносим ![]() за скобки. К оставшемуся интегралу применяем прием, который рассмотрен в первых примерах урока статьи Интегрирование некоторых дробей.
за скобки. К оставшемуся интегралу применяем прием, который рассмотрен в первых примерах урока статьи Интегрирование некоторых дробей.
(2) В подынтегральной функции почленно делим числитель на знаменатель.
(3) Используем свойство линейности неопределенного интеграла. В последнем интеграле сразу подводим функцию под знак дифференциала.
(4) Берём оставшиеся интегралы. Обратите внимание, что в логарифме можно использовать скобки, а не модуль, так как ![]() .
.
(5) Проводим обратную замену, выразив из прямой замены ![]() «тэ»:
«тэ»: ![]()
Студенты-мазохисты могут продифференцировать ответ и получить исходную подынтегральную функцию, как только что это сделал я. Нет-нет, я-то в правильном смысле выполнил проверку =)
Как видите, в ходе решения пришлось использовать даже больше двух приемов решения, таким образом, для расправы с подобными интегралами нужны уверенные навыки интегрирования и не самый маленький опыт.
На практике, конечно же, чаще встречается квадратный корень, вот три примера для самостоятельного решения:
Пример 2
Найти неопределенный интеграл
![]()
Пример 3
Найти неопределенный интеграл
![]()
Пример 4
Найти неопределенный интеграл
![]()
Данные примеры однотипны, поэтому полное решение в конце статьи будет только для Примера 2, в Примерах 3-4 – одни ответы. Какую замену применять в начале решений, думаю, понятно. Почему я подобрал однотипные примеры? Часто встречаются в своем амплуа. Чаще, пожалуй, только что-нибудь вроде ![]() .
.
Но не всегда, когда под арктангенсом, синусом, косинусом, экспонентой и др. функциями находится корень из линейной функции, приходится применять сразу несколько методов. В ряде случаев удается «легко отделаться», то есть сразу после замены получается простой интеграл, который элементарно берётся. Самым легким из предложенных выше заданий является Пример 4, в нём после замены получается относительно несложный интеграл.
Метод сведения интеграла к самому себе
Остроумный и красивый метод. Немедленно рассмотрим классику жанра:
Пример 5
Найти неопределенный интеграл
![]()
Под корнем находится квадратный двучлен, и при попытке проинтегрировать данный пример чайник может мучаться часами. Такой интеграл берётся по частям и сводится к самому себе. В принципе не сложно. Если знаешь как.
Обозначим рассматриваемый интеграл латинской буквой ![]() и начнем решение:
и начнем решение:
![]()
Интегрируем по частям:


(1) Готовим подынтегральную функцию для деления.
(2) Делим числитель на знаменатель. Возможно, не всем понятно, распишу подробно:
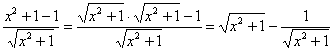
(3) Используем свойство линейности неопределенного интеграла.
(4) Берём последний интеграл («длинный» логарифм).
Теперь смотрим на самое начало решения:
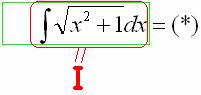
И на концовку:
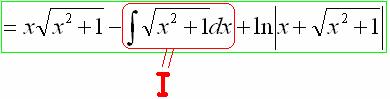
Что произошло? В результате наших манипуляций интеграл свёлся к самому себе!
Приравниваем начало и конец:
![]()
Переносим ![]() в левую часть со сменой знака:
в левую часть со сменой знака:
![]()
А двойку сносим в правую часть. В результате:
![]()
Или: ![]()
Константу ![]() , строго говоря, надо было добавить ранее, но приписал её в конце. Настоятельно рекомендую прочитать, в чём тут строгость:
, строго говоря, надо было добавить ранее, но приписал её в конце. Настоятельно рекомендую прочитать, в чём тут строгость:
Примечание: более строго заключительный этап решения выглядит так:
![]()
Таким образом:
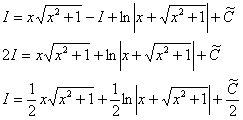
Константу ![]() можно переобозначить через
можно переобозначить через ![]() . Почему можно переобозначить? Потому что
. Почему можно переобозначить? Потому что ![]() всё равно принимает любые значения, и в этом смысле между константами
всё равно принимает любые значения, и в этом смысле между константами ![]() и
и ![]() нет никакой разницы.
нет никакой разницы.
В результате:
![]()
Подобный трюк с переобозначением константы широко используется в дифференциальных уравнениях. И там я буду строг. А здесь такая вольность допускается мной только для того, чтобы не путать вас лишними вещами и акцентировать внимание именно на самом методе интегрирования.
Пример 6
Найти неопределенный интеграл
![]()
Еще один типовой интеграл для самостоятельного решения. Полное решение и ответ в конце урока. Разница с ответом предыдущего примера будет!
Если под квадратным корнем находится квадратный трехчлен, то решение в любом случае сводится к двум разобранным примерам.
Например, рассмотрим интеграл ![]() . Всё, что нужно сделать – предварительно выделить полный квадрат:
. Всё, что нужно сделать – предварительно выделить полный квадрат:
![]() .
.
Далее проводится линейная замена, которая обходится «без всяких последствий»:
![]() , в результате чего получается интеграл
, в результате чего получается интеграл ![]() . Нечто знакомое, правда?
. Нечто знакомое, правда?
Или такой пример, с квадратным двучленом: ![]()
Выделяем полный квадрат: ![]()
И, после линейной замены ![]() , получаем интеграл
, получаем интеграл ![]() , который также решается по уже рассмотренному алгоритму.
, который также решается по уже рассмотренному алгоритму.
Рассмотрим еще два типовых примера на приём сведения интеграла к самому себе:
– интеграл от экспоненты, умноженной на синус;
– интеграл от экспоненты, умноженной на косинус.
В перечисленных интегралах по частям придется интегрировать уже два раза:
Пример 7
Найти неопределенный интеграл
![]()
Подынтегральная функция – экспонента, умноженная на синус.
Дважды интегрируем по частям и сводим интеграл к себе:
![]()
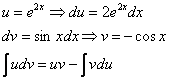
![]()
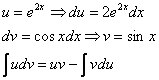

В результате двукратного интегрирования по частям интеграл свёлся к самому себе. Приравниваем начало и концовку решения:
![]()
Переносим ![]() в левую часть со сменой знака и выражаем наш интеграл:
в левую часть со сменой знака и выражаем наш интеграл:
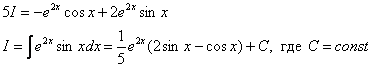
Готово. Попутно желательно причесать правую часть, т. е. вынести экспоненту за скобки, а в скобках расположить синус с косинусом в «красивом» порядке.
Теперь вернемся к началу примера, а точнее – к интегрированию по частям:
![]()
За ![]() мы обозначили экспоненту. Возникает вопрос, именно экспоненту всегда нужно обозначать за
мы обозначили экспоненту. Возникает вопрос, именно экспоненту всегда нужно обозначать за ![]() ? Не обязательно. На самом деле в рассмотренном интеграле принципиально без разницы, что обозначать за
? Не обязательно. На самом деле в рассмотренном интеграле принципиально без разницы, что обозначать за ![]() , можно было пойти другим путём:
, можно было пойти другим путём:
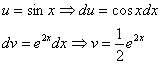
Почему такое возможно? Потому что экспонента превращается сама в себя (и при дифференцировании, и при интегрировании), синус с косинусом взаимно превращаются друг в друга (опять же – и при дифференцировании, и при интегрировании).
То есть за ![]() можно обозначить и тригонометрическую функцию. Но, в рассмотренном примере это менее рационально, поскольку появятся дроби. При желании можете попытаться решить данный пример вторым способом, ответы обязательно должны совпасть.
можно обозначить и тригонометрическую функцию. Но, в рассмотренном примере это менее рационально, поскольку появятся дроби. При желании можете попытаться решить данный пример вторым способом, ответы обязательно должны совпасть.
Пример 8
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения. Перед тем как решать, подумайте, что выгоднее в данном случае обозначить за ![]() , экспоненту или тригонометрическую функцию? Полное решение и ответ в конце урока.
, экспоненту или тригонометрическую функцию? Полное решение и ответ в конце урока.
И, конечно, не забывайте, что большинство ответов данного урока достаточно легко проверить дифференцированием!
Примеры были рассмотрены не самые сложные. На практике чаще встречаются интегралы, где константа есть и в показателе экспоненты и в аргументе тригонометрической функции, например: ![]() . Попутаться в подобном интеграле придется многим, частенько путаюсь и я сам. Дело в том, что в решении велика вероятность появления дробей, и очень просто что-нибудь по невнимательности потерять. Кроме того, велика вероятность ошибки в знаках, обратите внимание, что в показателе экспоненты есть знак «минус», и это вносит дополнительную трудность.
. Попутаться в подобном интеграле придется многим, частенько путаюсь и я сам. Дело в том, что в решении велика вероятность появления дробей, и очень просто что-нибудь по невнимательности потерять. Кроме того, велика вероятность ошибки в знаках, обратите внимание, что в показателе экспоненты есть знак «минус», и это вносит дополнительную трудность.
На завершающем этапе часто получается примерно следующее:
![]()
Даже в конце решения следует быть предельно внимательным и грамотно разобраться с дробями:
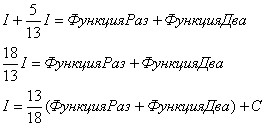
Интегрирование сложных дробей
Потихоньку подбираемся к экватору урока и начинаем рассматривать интегралы от дробей. Опять же, не все они суперсложные, просто по тем или иным причинам примеры были немного «не в тему» в других статьях.
Продолжаем тему корней
Пример 9
Найти неопределенный интеграл
![]()
В знаменателе под корнем находится квадратный трехчлен плюс за пределами корня «довесок» в виде «икса». Интеграл такого вида решается с помощью стандартной замены.
Решаем:
![]()
Замена тут проста:
![]()
Смотрим на жизнь после замены:
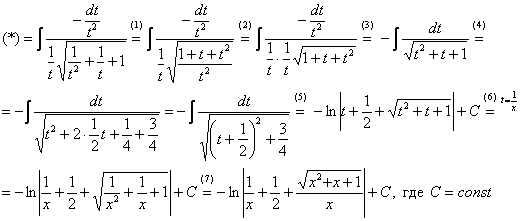
(1) После подстановки приводим к общему знаменателю слагаемые под корнем.
(2) Выносим ![]() из-под корня.
из-под корня.
(3) Числитель и знаменатель сокращаем на ![]() . Заодно под корнем я переставил слагаемые в удобном порядке. При определенном опыте шаги (1), (2) можно пропускать, выполняя прокомментированные действия устно.
. Заодно под корнем я переставил слагаемые в удобном порядке. При определенном опыте шаги (1), (2) можно пропускать, выполняя прокомментированные действия устно.
(4) Полученный интеграл, как вы помните из урока Интегрирование некоторых дробей, решается методом выделения полного квадрата. Выделяем полный квадрат.
(5) Интегрированием получаем заурядный «длинный» логарифм.
(6) Проводим обратную замену. Если изначально ![]() , то обратно:
, то обратно: ![]() .
.
(7) Заключительное действие направлено на прическу результата: под корнем снова приводим слагаемые к общему знаменателю и выносим из-под корня ![]() .
.
Пример 10
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения. Здесь к одинокому «иксу» добавлена константа, и замена почти такая же:
![]()
Единственное, что нужно дополнительно сделать – выразить «икс» из проводимой замены: ![]()
Полное решение и ответ в конце урока.
Иногда в таком интеграле под корнем может находиться квадратный двучлен, это не меняет способ решения, оно будет даже еще проще. Почувствуйте разницу:
Пример 11
Найти неопределенный интеграл
![]()
Пример 12
Найти неопределенный интеграл
![]()
Краткие решения и ответы в конце урока. Следует отметить, что Пример 11 является в точности биномиальным интегралом, метод решения которого рассматривался на уроке Интегралы от иррациональных функций.
Интеграл от неразложимого многочлена 2-й степени в степени
(многочлен в знаменателе)
Более редкий, но, тем не менее, встречающий в практических примерах вид интеграла.
Пример 13
Найти неопределенный интеграл
![]()
В знаменателе подынтегральной функции находится неразложимый на множители квадратный двучлен. Подчеркиваю, что неразложимость на множители является существенной особенностью. Если многочлен раскладывается на множители, то всё намного понятнее, например:
![]() – и далее применяется стандартный метод неопределенных коэффициентов.
– и далее применяется стандартный метод неопределенных коэффициентов.
Но вернёмся к примеру со счастливым номером 13 (честное слово, не подгадал). Этот интеграл тоже из разряда тех, с которыми можно изрядно промучиться, если не знаешь, как решать.
Решение начинается с искусственного преобразования:

Это приём, думаю, уже все понимают.
Полученный интеграл берётся по частям:
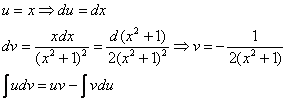
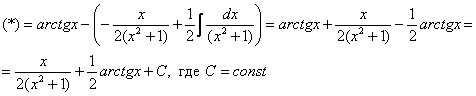
Готово.
Для интеграла вида ![]() (
(![]() – натуральное число) выведена рекуррентная формула понижения степени:
– натуральное число) выведена рекуррентная формула понижения степени:
![]() , где
, где ![]() – интеграл степенью ниже.
– интеграл степенью ниже.
Убедимся в справедливости данной формулы для прорешанного интеграла ![]() .
.
В данном случае: ![]() ,
, ![]() , используем формулу:
, используем формулу:
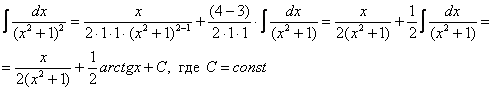
Как видите, ответы совпадают.
Пример 14
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения. В образце решения дважды последовательно использована вышеупомянутая формула.
Если под степенью находится неразложимый на множители квадратный трехчлен, то решение сводится к двучлену путем выделения полного квадрата, например:
![]()
Далее следует «безболезненная» линейная замена ![]() и получается знакомый интеграл
и получается знакомый интеграл ![]() .
.
Что делать, если дополнительно в числителе есть многочлен? В этом случае используется метод неопределенных коэффициентов, и подынтегральная функция раскладывается в сумму дробей. Но в моей практике такого примера не встречалось ни разу, поэтому я пропустил данный случай в статье Интегралы от дробно-рациональной функции, пропущу и сейчас. Если такой интеграл все-таки встретится, смотрите учебник – там всё просто. Не считаю целесообразным включать материал (даже несложный), вероятность встречи с которым стремится к нулю.
Интегрирование сложных тригонометрических функций
Прилагательное «сложный» для большинства примеров вновь носит во многом условный характер. Начнем с тангенсов и котангенсов в высоких степенях. С точки зрения используемых методов решения тангенс и котангенс – почти одно и тоже, поэтому я больше буду говорить о тангенсе, подразумевая, что продемонстрированный прием решения интеграла справедлив и для котангенса тоже.
На уроке Интегралы от тригонометрических функций мы разобрали интеграл от тангенса в квадрате. На уроке Как вычислить площадь фигуры? в примере 10 фигурировал тангенс в кубе. В том примере для нахождения интеграла от тангенса в кубе мы применяли тригонометрическую формулу ![]() . Интеграл от тангенса в четвертой, пятой степени (редко в более высоких степенях) решается с помощью этой же формулы!
. Интеграл от тангенса в четвертой, пятой степени (редко в более высоких степенях) решается с помощью этой же формулы!
Пример 15
Найти неопределенный интеграл
![]()
Идея решения подобных интегралов состоит в том, чтобы с помощью формулы ![]() «развалить» исходный интеграл на несколько более простых интегралов:
«развалить» исходный интеграл на несколько более простых интегралов:
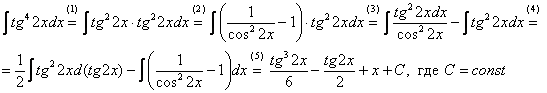
(1) Готовим подынтегральную функцию к применению формулы.
(2) Для одного из множителей используем формулу ![]()
(3) Раскрываем скобки и сразу же используем свойство линейности неопределенного интеграла.
(4) В первом интеграле используем метод подведения функции под знак дифференциала. Во втором интеграле еще раз используем формулу ![]() , в данном случае
, в данном случае ![]() .
.
(5) Берём все три интеграла и получаем ответ.
Пример 16
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения. Для котангенса существует аналогичная формула: ![]() . Полное решение и ответ в конце урока.
. Полное решение и ответ в конце урока.
Если возникли затруднения или недопонимание, следует вернуться к уроку Интегралы от тригонометрических функций.
На вышеупомянутом уроке мы рассматривали универсальную тригонометрическую подстановку для решения определенного вида интегралов от тригонометрических функций. Недостаток универсальной тригонометрической подстановки заключается в том, что при её применении часто возникают громоздкие интегралы с трудными вычислениями. И в ряде случаев универсальной тригонометрической подстановки можно избежать!
Рассмотрим еще один канонический пример, интеграл от единицы, деленной на синус:
Пример 17
Найти неопределенный интеграл
![]()
Здесь можно использовать универсальную тригонометрическую подстановку и получить ответ, но существует более рациональный путь. Я приведу полное решение с комментами к каждому шагу:

(1) Используем тригонометрическую формулу синуса двойного угла ![]() .
.
(2) Проводим искусственное преобразование: В знаменателе делим и умножаем на ![]() .
.
(3) По известной формуле в знаменателе превращаем дробь в тангенс.
(4) Подводим функцию под знак дифференциала.
(5) Берём интеграл.
Пара простых примеров для самостоятельного решения:
Пример 18
Найти неопределенный интеграл
![]()
Указание: Самым первым действием следует использовать формулу приведения ![]() и аккуратно провести аналогичные предыдущему примеру действия.
и аккуратно провести аналогичные предыдущему примеру действия.
Пример 19
Найти неопределенный интеграл
![]()
Ну, это совсем простой пример.
Полные решения и ответы в конце урока.
Думаю, теперь ни у кого не возникнет проблем с интегралами:
![]() и т. п.
и т. п.
В чём состоит идея метода? Идея состоит в том, чтобы с помощью преобразований, тригонометрических формул организовать в подынтегральной функции только тангенсы и производную тангенса ![]() . То есть речь идет о замене:
. То есть речь идет о замене: ![]() . В Примерах 17-19 мы фактически и применяли данную замену, но интегралы были настолько просты, что дело обошлось эквивалентным действием – подведением функции под знак дифференциала.
. В Примерах 17-19 мы фактически и применяли данную замену, но интегралы были настолько просты, что дело обошлось эквивалентным действием – подведением функции под знак дифференциала.
Аналогичные рассуждения, как я уже оговаривался, можно провести для котангенса.
Существует и формальная предпосылка для применения вышеуказанной замены:
Сумма степеней косинуса и синуса – целое отрицательное ЧЁТНОЕ число, например:
для интеграла ![]() – целое отрицательное ЧЁТНОЕ число.
– целое отрицательное ЧЁТНОЕ число.
! Примечание: если подынтегральная функция содержит ТОЛЬКО синус или ТОЛЬКО косинус, то интеграл берётся и при отрицательной нечётной степени (простейшие случаи – в Примерах № 17, 18).
Рассмотрим пару более содержательных заданий на это правило:
Пример 20
Найти неопределенный интеграл
![]()
Сумма степеней синуса и косинуса ![]() : 2 – 6 = –4 – целое отрицательное ЧЁТНОЕ число, значит, интеграл можно свести к тангенсам и его производной:
: 2 – 6 = –4 – целое отрицательное ЧЁТНОЕ число, значит, интеграл можно свести к тангенсам и его производной:

(1) Преобразуем знаменатель.
(2) По известной формуле получаем ![]() .
.
(3) Преобразуем знаменатель.
(4) Используем формулу ![]() .
.
(5) Подводим функцию под знак дифференциала.
(6) Проводим замену ![]() . Более опытные студенты замену могут и не проводить, но все-таки лучше заменить тангенс одной буквой – меньше риск запутаться.
. Более опытные студенты замену могут и не проводить, но все-таки лучше заменить тангенс одной буквой – меньше риск запутаться.
Далее берётся простой интеграл и проводится обратная замена.
Пример 21
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения.
Держитесь, начинаются чемпионские раунды =)
Зачастую в подынтегральной функции находится «солянка»:
Пример 22
Найти неопределенный интеграл
![]()
В этом интеграле изначально присутствует тангенс, что сразу наталкивает на уже знакомую мысль:

Искусственное преобразование в самом начале и остальные шаги оставлю без комментариев, поскольку обо всем уже говорилось выше.
Пара творческих примеров для самостоятельного решения:
Пример 23
Найти неопределенный интеграл
![]()
Пример 24
Найти неопределенный интеграл
![]()
Да, в них, конечно, можно понизить степени синуса, косинуса, использовать универсальную тригонометрическую подстановку, но решение будет гораздо эффективнее и короче, если его провести через тангенсы. Полное решение и ответы в конце урока
У многих читателей могло сложиться впечатления, что я немного подустал. Отнюдь. За окном февральский ветер – самая атмосфера для лекций. Естественно, данная страничка создана не за один день, я успел несколько раз побриться, регулярно кушаю и так далее. К тому же, загружать студентов – удовольствие бесконечное =). …Шутка! На самом деле моя миссия – разгружать посетителей сайта. Вагонами.
Переходим к заключительному пункту познавательного путешествия в мир сложных интегралов:
Интеграл от корня из дроби
Интеграл, который мы рассмотрим, встречается достаточно редко, но я буду очень рад, если единственный пример данного параграфа вам поможет.
Корнями всё начиналось, корнями и закончится. Рассмотрим неопределенный интеграл:
![]() , где
, где ![]() – числа. Руководствуясь законом подлости, считаем, что все эти числа коэффициенты не равны нулю. Это уже не смешно, так обычно и бывает.
– числа. Руководствуясь законом подлости, считаем, что все эти числа коэффициенты не равны нулю. Это уже не смешно, так обычно и бывает.
В подынтегральной функции у нас находится корень, а под корнем – дробь, в числителе и знаменателе которой располагаются линейные функции.
Метод стар – нужно избавиться от корня. Стар и уныл, но сейчас станет веселее, поскольку придется проводить громоздкую замену.
Замена, с помощью которой мы гарантированно избавимся от корня, очевидна:
![]() , при этом
, при этом ![]() , т. к. корень чётный.
, т. к. корень чётный.
Теперь нужно выразить «икс» и найти, чему равен дифференциал ![]() .
.
Выражаем «икс»:
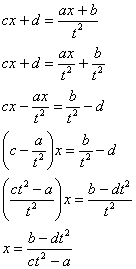
Теперь найдем дифференциал:
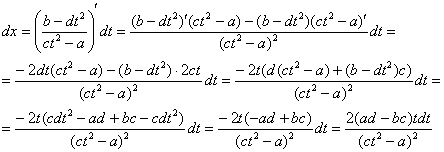
Зачем были эти нелепые скучные телодвижения?
Я вывел готовые формулы, которыми можно пользовать при решении интеграла вида ![]() !
!
Формулы замены таковы:
![]()
Это было ни в коем случае не хвастовство, просто я не смог быстро найти эти формулы в близлежащей литературе и Сети – оказалось проще вывести. Да и может быть кто-нибудь для реферата возьмет.
Опять – двадцать пять, заключительный пример:
Пример 25
Найти неопределенный интеграл
![]()
Проведем замену: ![]()
В данном примере: ![]()
![]()
Таким образом:
![]()
Еще куда ни шло, могло всё оказаться значительно хуже. Такой интеграл, кстати, уже фигурировал в Примере 13. Интегрируем по частям:
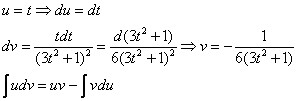
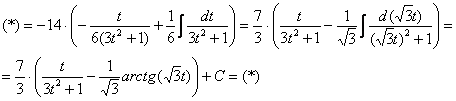
Проведем обратную замену. Если изначально ![]() , то обратно:
, то обратно:
![]()
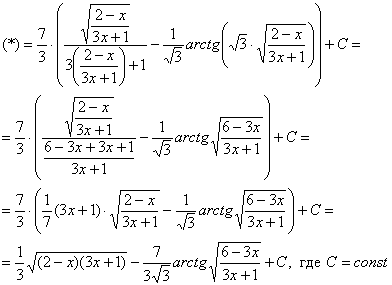
Некоторым страшно, а я это продифференцировал, ответ верный!
Иногда встречаются интегралы вида ![]() ,
, ![]() , но это нужно быть либо слишком умным либо попасть под раздачу. Идея та же – избавиться от корня, причем во втором случае, как все догадались, следует проводить подстановку
, но это нужно быть либо слишком умным либо попасть под раздачу. Идея та же – избавиться от корня, причем во втором случае, как все догадались, следует проводить подстановку ![]() и самостоятельно выводить, чему будет равняться дифференциал
и самостоятельно выводить, чему будет равняться дифференциал ![]() .
.
Теперь вам практически любой интеграл по силам, успехов!
Решения и ответы:
Пример 2. Решение:
![]()
Проведем замену:
![]()
![]()
Интегрируем по частям:
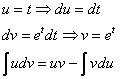
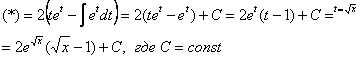
Пример 3. Ответ:
![]()
Пример 4. Ответ:
![]()
Пример 6. Решение:
![]()
Интегрируем по частям:
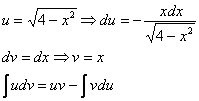

Таким образом:
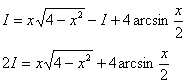
В результате:
![]()
Пример 8. Решение:
Дважды интегрируем по частям и сводим интеграл к себе:
![]()
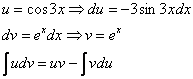
![]()
![]()
![]()
Таким образом:
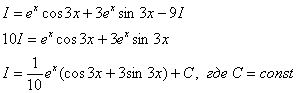
Пример 10. Решение:
![]()
Проведем замену: ![]()
![]()

Пример 11. Решение:
![]()
Замена: ![]()
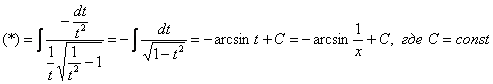
Пример 12. Решение:
![]()
Замена: ![]()
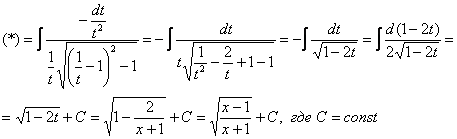
Пример 14. Решение:
![]()
Дважды используем рекуррентную формулу ![]()
![]()
![]()
![]()
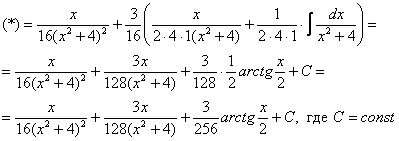
Пример 16. Решение:
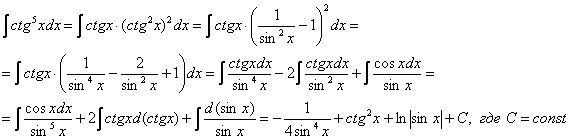
Пример 18. Решение:
![]()
Используем формулу приведения: ![]() и формулу двойного угла:
и формулу двойного угла: ![]() .
.

Пример 19. Решение:
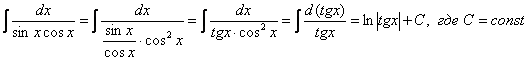
Пример 21. Решение:
–3 – 3 = –6 – целое отрицательное ЧЁТНОЕ число
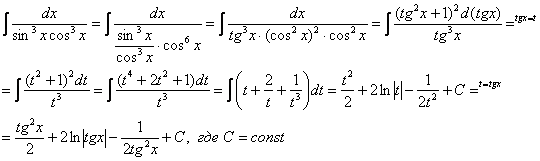
Пример 23. Решение:

Пример 24. Решение:

Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright