


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Непрерывная случайная величина и её функция распределения.
Функция плотности распределения
О непрерывной случайной величине (НСВ) я неоднократно упоминал в предыдущих статьях, и поэтому, если вы зашли с поисковика и/или не совсем в теме, то начните с первого урока о случайных величинах. После чего продолжаем и сразу вспоминаем разницу:
– В отличие от дискретной случайной величины, НСВ может принять любое действительное значение из некоторого промежутка ненулевой длины, что делает невозможным её представление в виде таблицы (т.к. действительных чисел несчётно много). В этой связи непрерывную случайную величину задают функциями двух типов, названия которых вы видите в заголовке.
Функция распределения непрерывной случайной величины ![]() определяется точно так же, как и функция распределения ДСВ:
определяется точно так же, как и функция распределения ДСВ:
![]() – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение, МЕНЬШЕЕ, чем переменная
примет значение, МЕНЬШЕЕ, чем переменная ![]() , которая «пробегает» все значения от «минус» до «плюс» бесконечности. Таким образом, учитываются все значения, которые В ПРИНЦИПЕ может принять произвольная случайная величина. С увеличением
, которая «пробегает» все значения от «минус» до «плюс» бесконечности. Таким образом, учитываются все значения, которые В ПРИНЦИПЕ может принять произвольная случайная величина. С увеличением ![]() функция распределения «накапливает» (суммирует) вероятности, а значит, является неубывающей и изменяется в пределах
функция распределения «накапливает» (суммирует) вероятности, а значит, является неубывающей и изменяется в пределах ![]() . По этой причине её иногда называют интегральной функцией распределения.
. По этой причине её иногда называют интегральной функцией распределения.
Важной особенностью является тот факт, что функция распределения ЛЮБОЙ непрерывной случайной величины всегда и всюду непрерывна! Часто её можно встретить в кусочном виде, например:
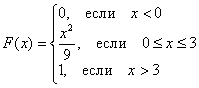
однако в точках «стыка» всё хорошо:
![]()
и если там разрыв, то вы имеете дело с опечаткой или откровенной ошибкой!
! Но сама по себе непрерывность и ноль слева, единица справа – ещё не означают, что перед нами функция распределения.
При ручном построении чертежа целесообразно найти опорные точки; в нашем примере удобно взять: ![]() и плавно-плавно провести карандашом кусочек параболы
и плавно-плавно провести карандашом кусочек параболы ![]() :
:
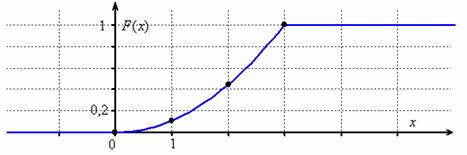
Напоминаю, что левый нижний луч следует прочертить жирно (чтобы он не сливался с осью), а правый верхний луч продолжить за остриё оси (т.к. график бесконечен). Также не забываем, что ![]() не может убывать, и если вдруг окажется, что какой-то кусок графика идёт «сверху вниз», то ищите ошибку или опять же – имеет место опечатка. А может просто дрогнула рука :)
не может убывать, и если вдруг окажется, что какой-то кусок графика идёт «сверху вниз», то ищите ошибку или опять же – имеет место опечатка. А может просто дрогнула рука :)
Что касаемо масштаба, то смотрим по ситуации, чаще всего оптимальный масштаб составляет 1 ед. = 1 см (две клетки), но поскольку я строю графики не от руки, то особо не слежу за пропорциями – в данном случае по оси ординат вышло примерно в 2 раза больше, чем по оси абсцисс.
Теперь вернёмся к смыслу функции распределения и рассмотрим пару конкретных «икс»:
![]() – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение, МЕНЬШЕЕ, чем –1;
примет значение, МЕНЬШЕЕ, чем –1;
![]() – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение, МЕНЬШЕЕ, чем 4.
примет значение, МЕНЬШЕЕ, чем 4.
Ну, и очевидно, что рассматриваемая случайная величина принимает случайные, наперёд неизвестные значения из отрезка ![]() . Если вкладывать в задачу содержательный смысл, то это может быть случайная продолжительность некоего процесса (в секундах, например), или масса либо размер случайно выбранного объекта (например, крупинки песка). И тому подобное – примеров масса. Конкретные задачи непременно будут, но прежде остановимся на технической стороне вопроса.
. Если вкладывать в задачу содержательный смысл, то это может быть случайная продолжительность некоего процесса (в секундах, например), или масса либо размер случайно выбранного объекта (например, крупинки песка). И тому подобное – примеров масса. Конкретные задачи непременно будут, но прежде остановимся на технической стороне вопроса.
Вероятность того, что случайная величина примет значение из некоторого промежутка рассчитывается ещё проще, чем для дискретной случайной величины. Здесь нет никакой Санта-Барбары: отрезок ли ![]() нам дан, полуинтервал
нам дан, полуинтервал ![]() или интервал
или интервал ![]() , соответствующую вероятность можно вычислить по единой формуле:
, соответствующую вероятность можно вычислить по единой формуле:
![]()
Примечание: в следующем параграфе мы обоснуем это утверждение
Например:
![]() – вероятность того, что случайная величина примет значение из отрезка
– вероятность того, что случайная величина примет значение из отрезка ![]() . И точно такими же будут вероятности
. И точно такими же будут вероятности ![]() ;
;
![]() – вероятность того, что случайная величина примет значение из отрезка
– вероятность того, что случайная величина примет значение из отрезка ![]() ;
;
![]() – вероятность того, что случайная величина примет значение из интервала
– вероятность того, что случайная величина примет значение из интервала ![]() ;
;
и так далее.
Наверное, вы подметили, что на участках одинаковой длины результаты получились разными: ![]() . И возникает вопрос: как оценить эту «концентрацию» вероятностей на различных промежутках? – ведь функция распределения
. И возникает вопрос: как оценить эту «концентрацию» вероятностей на различных промежутках? – ведь функция распределения ![]() характеризует накопление вероятностей по мере увеличения
характеризует накопление вероятностей по мере увеличения ![]() , и много раз вычислять
, и много раз вычислять ![]() что-то неохота.
что-то неохота.
Эффективный ответ на поставленный вопрос даёт
функция ПЛОТНОСТИ распределения вероятностей
или дифференциальная функция распределения. Она представляет собой производную функции распределения: ![]() .
.
Примечание: для дискретной случайной величины такой функции не существует
В нашем примере:
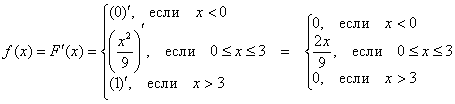
То есть, всё очень просто – берём производную от каждого куска, и порядок.
Но настоящий порядок состоит в том, что несобственный интеграл от ![]() с пределами интегрирования от «минус» до «плюс» бесконечности:
с пределами интегрирования от «минус» до «плюс» бесконечности:
![]() – равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция найдена как производная, то
– равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция найдена как производная, то ![]() – не является функцией распределения (несмотря на какие бы то ни было другие признаки).
– не является функцией распределения (несмотря на какие бы то ни было другие признаки).
Проверим «подлинность» наших функций. Если случайная величина ![]() принимает значения из конечного промежутка, то всё дело сводится к вычислению определённого интеграла. В силу свойства аддитивности:
принимает значения из конечного промежутка, то всё дело сводится к вычислению определённого интеграла. В силу свойства аддитивности:
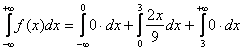
Совершенно понятно, что левый и правый интегралы равны нулю и нам осталось вычислить:
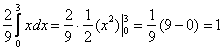 , что и требовалось проверить. С вероятностной точки зрения это означает, что случайная величина
, что и требовалось проверить. С вероятностной точки зрения это означает, что случайная величина ![]() достоверно примет одно из значений отрезка
достоверно примет одно из значений отрезка ![]() . Геометрически же это означает, что площадь между осью
. Геометрически же это означает, что площадь между осью ![]() и графиком
и графиком ![]() равна единице, в данном случае речь идёт о площади треугольника
равна единице, в данном случае речь идёт о площади треугольника ![]() . Сторона
. Сторона ![]() является фрагментом прямой
является фрагментом прямой ![]() и для её построения достаточно найти точку
и для её построения достаточно найти точку ![]() :
:
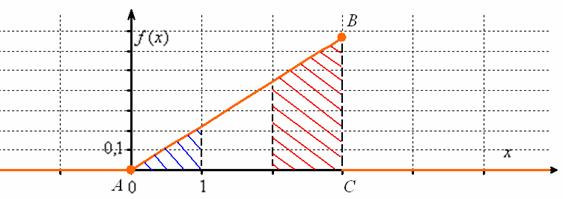
Ну вот, стало всё наглядно – где бОльшая площадь, там и более вероятные значения. Так как функция плотности «собирает под собой» вероятности, то она тоже неотрицательна ![]() и её график не может располагаться ниже оси
и её график не может располагаться ниже оси ![]() . Следует также отметить, что в общем случае эта функция разрывна (следим, где «жирные» точки!).
. Следует также отметить, что в общем случае эта функция разрывна (следим, где «жирные» точки!).
Теперь разберём весьма любопытный факт: поскольку действительных чисел несчётно много, то вероятность того, что случайная величина ![]() примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадались:
примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадались:
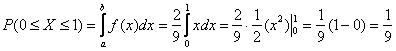 (синяя площадь на чертеже) – вероятность того, что случайная величина примет значение из отрезка
(синяя площадь на чертеже) – вероятность того, что случайная величина примет значение из отрезка ![]() ;
;
![]() (красная площадь) – вероятность того, что случайная величина примет значение из отрезка
(красная площадь) – вероятность того, что случайная величина примет значение из отрезка ![]() .
.
По той причине, что отдельно взятые значения можно не принимать во внимание, с помощью этих же интегралов рассчитываются и вероятности по интервалам / полуинтервалам, в частности:
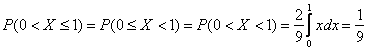
Этим же объяснятся аналогичная «вольность» с функцией ![]() .
.
Возможно, кто-то спросит: а зачем считать интегралы, если есть функция ![]() ?
?
А дело в том, что во многих задачах непрерывная случайная величина ИЗНАЧАЛЬНО задана функцией ![]() плотности распределения, которая ТОЖЕ однозначно определяет случайную величину. Но, как вариант, можно сначала найти функцию
плотности распределения, которая ТОЖЕ однозначно определяет случайную величину. Но, как вариант, можно сначала найти функцию ![]() (с помощью тех же интегралов), после чего использовать «лёгкий способ»
(с помощью тех же интегралов), после чего использовать «лёгкий способ» бросить курить отыскания вероятностей. Впрочем, об этом чуть позже:
Пример 1
Непрерывная случайная величина ![]() задана своей функцией распределения:
задана своей функцией распределения:
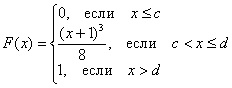
Найти значения ![]() и функцию
и функцию ![]() . Проверить, что
. Проверить, что ![]() действительно является функцией плотности распределения. Вычислить вероятности
действительно является функцией плотности распределения. Вычислить вероятности ![]() . Построить графики
. Построить графики ![]() .
.
Тренируемся самостоятельно! Если возникнут затруднения, то внимательно перечитайте вышеизложенный материал. Краткое решение и ответ в конце урока.
Вообще, типовые задачи на непрерывную случайную величину можно разделить на 2 большие группы: 1) когда дана функция ![]() , 2) когда дана функция
, 2) когда дана функция ![]() .
.
В первом случае не составляет никаких трудностей отыскать функцию плотности распределения – почти всегда производные не то что простЫ, а примитивны (в чём мы недавно убедились). Но вот когда НСВ задана функцией ![]() , то нахождение функции распределения – есть более кропотливый процесс:
, то нахождение функции распределения – есть более кропотливый процесс:
Пример 2
Непрерывная случайная величина ![]() задана функцией плотности распределения:
задана функцией плотности распределения:
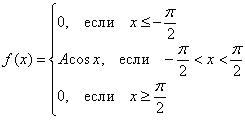
Найти значение ![]() и составить функцию распределения вероятностей. Вычислить
и составить функцию распределения вероятностей. Вычислить ![]() . Построить графики
. Построить графики ![]() .
.
Решение: найдём константу ![]() . Это классика. В подавляющем большинстве задач вам не предложат готовую функцию плотности. Используем свойство
. Это классика. В подавляющем большинстве задач вам не предложат готовую функцию плотности. Используем свойство ![]() . В данном случае:
. В данном случае:

На практике нулевые интегралы можно опускать, а константу сразу выносить за знак интеграла:
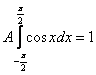
Пользуясь чётностью подынтегральной функции, вычислим:
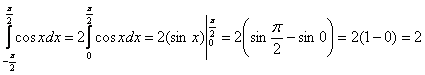 и подставим результат в уравнение:
и подставим результат в уравнение:
![]() , откуда выразим
, откуда выразим ![]()
Таким образом, функция плотности распределения:
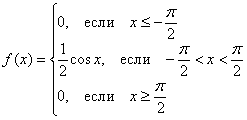
Выполним проверку, а именно, вычислим тот же самый интеграл, но уже с известной константой. Для разнообразия я не буду пользоваться чётностью:
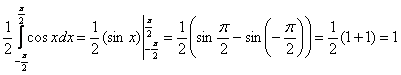 , что и требовалось проверить.
, что и требовалось проверить.
Обратите внимание, что только при ![]() – и только при этом значении, предложенная в условии функция является функцией плотности распределения. Ну и тут не лишним будет проконтролировать, что на интервале
– и только при этом значении, предложенная в условии функция является функцией плотности распределения. Ну и тут не лишним будет проконтролировать, что на интервале ![]() , т.е. условие неотрицательности выполнено. Доверяй условию, да проверяй ;) Не раз и не два мне встречались функции, которые в принципе не могли быть плотностью, что говорило об опечатках или о невнимательности авторов задач.
, т.е. условие неотрицательности выполнено. Доверяй условию, да проверяй ;) Не раз и не два мне встречались функции, которые в принципе не могли быть плотностью, что говорило об опечатках или о невнимательности авторов задач.
Теперь начинается самое интересное. Функция распределения вероятностей – есть интеграл:
![]()
Так как наша ![]() состоит из трёх кусков, то решение разобьётся на 3 шага:
состоит из трёх кусков, то решение разобьётся на 3 шага:
1) На промежутке ![]() , поэтому:
, поэтому:
![]()
2) На интервале ![]() , и мы прицепляем следующий вагончик:
, и мы прицепляем следующий вагончик:
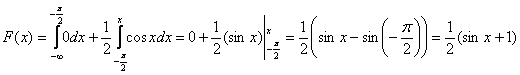
При подстановке верхнего предела интегрирования можно считать, что вместо «икс» мы подставляем «икс». Если же возник вопрос с пределом нижним, то вспоминаем график синусоиды или нечётность синуса ![]() с тригонометрической таблицей.
с тригонометрической таблицей.
3) И, наконец, на ![]() , и детский паровозик отправляется в путь:
, и детский паровозик отправляется в путь:

! А вот в этом задании нулевые интегралы пропускать НЕ НАДО. Чтобы показать своё понимание функции распределения ;) К тому же, они могут оказаться вовсе не нулевыми, и тогда придётся иметь дело с интегралами несобственными. Соответствующие примеры я обязательно разберу ниже.
Записываем наши достижения под единую скобку:
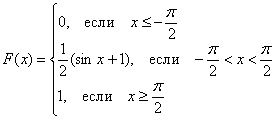
С высокой вероятностью всё правильно, но, тем не менее, устно возьмём производную 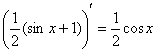 , а также «прозвоним» точки «стыка»:
, а также «прозвоним» точки «стыка»:
![]()
Правильность решения можно проконтролировать и в ходе построения графика, но, во-первых, он не всегда требуется, а во-вторых, до сего момента можно успеть «наломать дров». Ибо вероятности попадания в интервал чаще находят с помощью функции распределения:
![]()
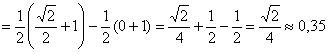 – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение из промежутка
примет значение из промежутка ![]()
Но ценители интегрального исчисления, конечно же, не откажут себе в удовольствии:
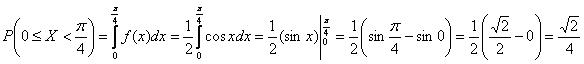 , что, кстати, не труднее. И проверочка заодно получилась.
, что, кстати, не труднее. И проверочка заодно получилась.
Выполним чертежи. График ![]() представляет собой
представляет собой косинусоиду, сжатую вдоль ординат в 2 раза:
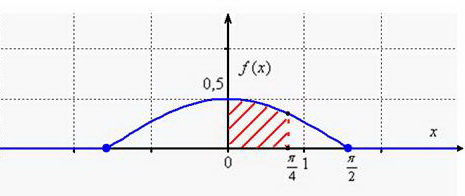
Тот редкий случай, когда функция плотности непрерывна.
Значение ![]() численно равно заштрихованной площади – это я специально сделал, чтобы напомнить вероятностный смысл функции плотности. И вся площадь под «дугой» равна единице, то есть, достоверным является тот факт, что случайная величина примет значение из интервала
численно равно заштрихованной площади – это я специально сделал, чтобы напомнить вероятностный смысл функции плотности. И вся площадь под «дугой» равна единице, то есть, достоверным является тот факт, что случайная величина примет значение из интервала ![]() . Заметьте, что значения
. Заметьте, что значения ![]() , согласно условию, невозможны.
, согласно условию, невозможны.
Осталось изобразить функцию распределения. График ![]() представляет собой сжатую в 2 раза вдоль оси ординат синусоиду, сдвинутую на
представляет собой сжатую в 2 раза вдоль оси ординат синусоиду, сдвинутую на ![]() вверх:
вверх:
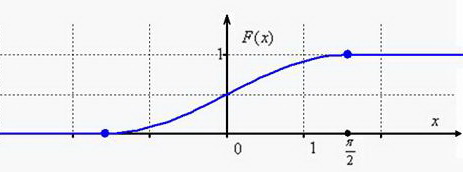
В принципе, тут можно не заморачиваться преобразованием графиков, а найти несколько опорных точек и догадаться, как выглядит кривая (тригонометрическая таблица в помощь). Но «любительский» подход чреват тем, что график получится принципиально не точным. Так, в нашем примере в точке ![]() существует перегиб графика, и велик риск неверно отобразить его выпуклость / вогнутость.
существует перегиб графика, и велик риск неверно отобразить его выпуклость / вогнутость.
Чертежи желательно расположить так, чтобы оси ординат лежали ровненько одна под другой. Это будет хорошим тоном.
И я так чувствую, вам уже не терпится проверить свои силы. Как водится, пример попроще:
Пример 3
Задана плотность распределения вероятностей непрерывной случайной величины ![]() :
:
![]()
Требуется:
1) определить коэффициент ![]() ;
;
2) найти функцию распределения ![]() ;
;
3) построить графики ![]() ;
;
4) найти вероятность того, что ![]() примет значение из промежутка
примет значение из промежутка ![]()
и задачка поинтереснее:
Пример 4
Непрерывная случайная величина ![]() задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:
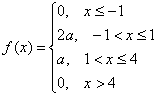
Найти значение ![]() и построить график плотности распределения. Найти функцию распределения вероятностей
и построить график плотности распределения. Найти функцию распределения вероятностей ![]() и построить её график. Вычислить вероятность
и построить её график. Вычислить вероятность ![]() .
.
Дерзайте! Свериться с решением можно внизу страницы.
И в заключение 1-й части урока обещанные случаи с несобственными интегралами:
Пример 5
Непрерывная случайная величина ![]() задана своей плотностью распределения:
задана своей плотностью распределения:
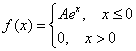
Найти коэффициент ![]() и функцию распределения
и функцию распределения ![]() . Построить графики.
. Построить графики.
Решение: по свойству функции плотности распределения:
![]()
В данной задаче ![]() состоит из 2 частей, поэтому:
состоит из 2 частей, поэтому:
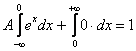
Правый интеграл равен нулю, а вот левый – есть «живой» несобственный интеграл с бесконечным нижним пределом:
![]()
Таким образом, наше уравнение превратилось в готовый результат:
![]()
и функция плотности:
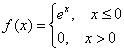
Функция ![]() , как нетрудно понять, отыскивается в 2 шага:
, как нетрудно понять, отыскивается в 2 шага:
1) На промежутке ![]() , следовательно:
, следовательно:
![]() – вот такая вот у нас замечательная экспонента. Как птица Феникс.
– вот такая вот у нас замечательная экспонента. Как птица Феникс.
2) На интервале ![]() и:
и:
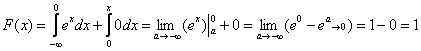 , что и должно получиться.
, что и должно получиться.
В результате:
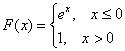
Для построения графиков найдём пару опорных точек: ![]() и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:
и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:
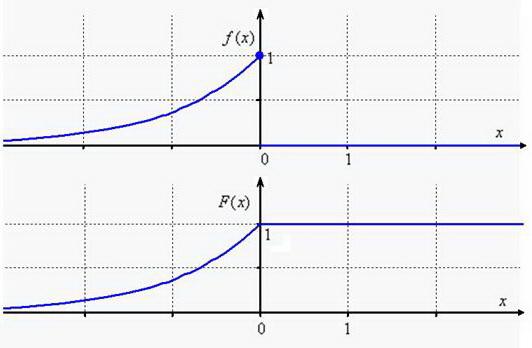
Заметьте, что теоретически случайная величина ![]() может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при
может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при ![]() .
.
Ещё более интересное задание для самостоятельного изучения:
Пример 6
Проверить, что ![]() является функцией плотности распределения вероятностей непрерывной случайной величины. Найти
является функцией плотности распределения вероятностей непрерывной случайной величины. Найти ![]() и выполнить чертежи.
и выполнить чертежи.
Здесь случайная величина теоретически принимает вообще ВСЕ действительные значения, т.к. ![]() определена при любом «икс». В ходе проверки
определена при любом «икс». В ходе проверки ![]() на плотность удобно использовать чётность подынтегральной функции в несобственном интеграле, а для нахождения самого интеграла нужно представить
на плотность удобно использовать чётность подынтегральной функции в несобственном интеграле, а для нахождения самого интеграла нужно представить ![]() и избавиться от трёхэтажности дроби. Самостоятельно выясните, как будут выглядеть графики – статья об асимптотах в помощь.
и избавиться от трёхэтажности дроби. Самостоятельно выясните, как будут выглядеть графики – статья об асимптотах в помощь.
Жду вас во 2-й части урока, посвящённой числовым характеристикам НСВ. Постарайтесь освоить её как можно скорее – по «горячим» знаниям и навыкам!
Решения и ответы:
Пример 1. Решение: в силу непрерывности функции распределения:
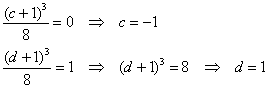
Таким образом:
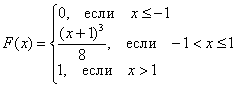
Контроль: ![]()
Найдём функцию плотности распределения:
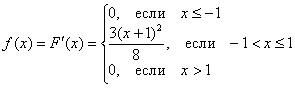
Покажем, что ![]() действительно является функцией плотности:
действительно является функцией плотности:
1) Для любого значения ![]() , в частности, на среднем промежутке:
, в частности, на среднем промежутке: ![]()
Внимание! Без 1-го пункта обойтись нельзя!
2) ![]()
Таким образом, найденная функция действительно является функцией плотности распределения.
Требуемые вероятности выгоднее вычислить с помощью функции распределения:
![]() – вероятность того, что случайная величина примет значение из полуинтервала
– вероятность того, что случайная величина примет значение из полуинтервала ![]() ;
;
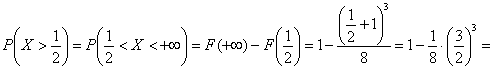
![]() – вероятность того, что случайная величина примет значение, больше, чем
– вероятность того, что случайная величина примет значение, больше, чем ![]() .
.
Построим графики ![]() :
:
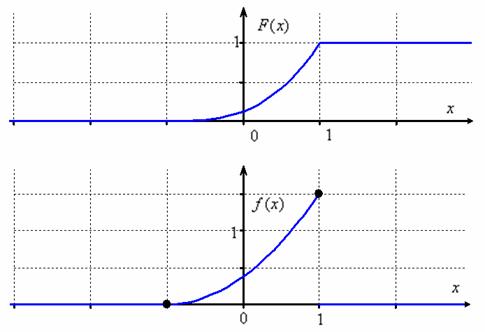
Пример 3. Решение:
1) По свойству функции плотности распределения:
![]()
В данной задаче:
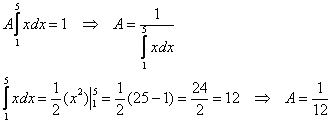
Таким образом, искомая плотность:
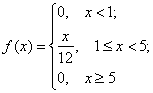
2) Функцию распределения найдём с помощью формулы ![]() :
:
– если ![]() то
то ![]() и
и ![]() ;
;
– если ![]() то
то ![]() и
и ![]() ;
;
– если ![]() то
то ![]() и:
и:
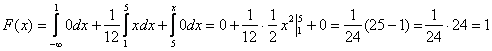 .
.
Таким образом:
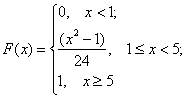
3) Выполним чертежи:
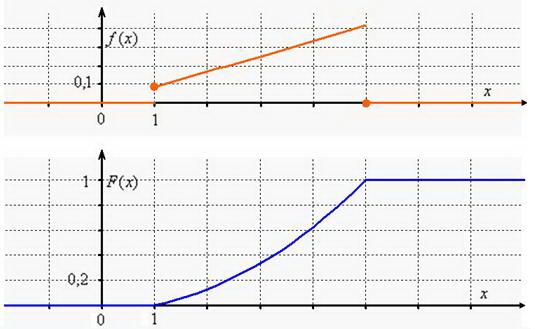
4) Найдём вероятность того, что случайная величина ![]() примет значение из промежутка
примет значение из промежутка ![]() :
:
![]()
Пример 4. Решение: функция плотности распределения вероятности обладает свойством ![]() . В данном случае:
. В данном случае:

Таким образом, функция плотности распределения:
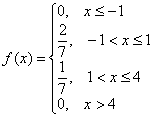
Выполним чертеж:
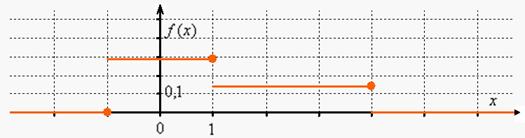
Составим функцию распределения вероятностей ![]() :
:
1) Если ![]() , то
, то ![]() и
и ![]()
2) Если ![]() , то
, то ![]() и
и ![]()
3) Если ![]() , то
, то ![]() и:
и:
![]()
4) Если ![]() , то
, то ![]() и:
и:
![]()
Таким образом:
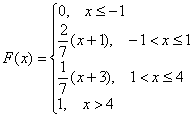 ,
,
Выполним чертеж:
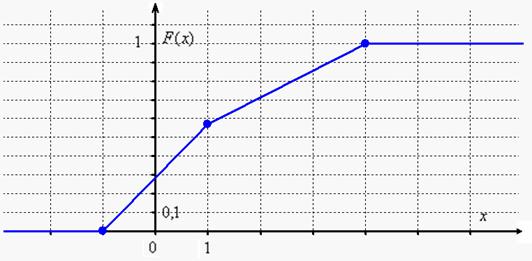
Вычислим ![]() – вероятность того, что случайная величина
– вероятность того, что случайная величина ![]() примет значение из интервала
примет значение из интервала ![]() .
.
Пример 6. Решение: проверим, что функция ![]() является функцией плотности:
является функцией плотности:
1) Поскольку экспоненциальная функция положительна, то ![]() для любого
для любого ![]() , значит, свойство неотрицательности функции плотности выполнено.
, значит, свойство неотрицательности функции плотности выполнено.
2) Проверим выполнение свойства ![]() .
.
Сначала удобно найти первообразную:
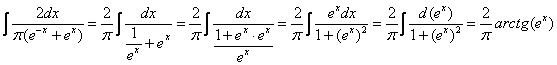 (константу добавлять не нужно).
(константу добавлять не нужно).
Используем чётность подынтегральной функции:
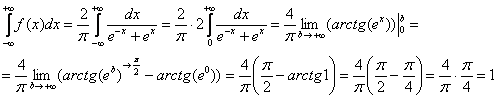
Вывод: ![]() является функцией плотности распределения вероятностей непрерывной случайной величины, что и требовалось проверить.
является функцией плотности распределения вероятностей непрерывной случайной величины, что и требовалось проверить.
Найдём функцию распределения:
![]()
![]() – для всех
– для всех ![]() .
.
Выполним чертёжи:
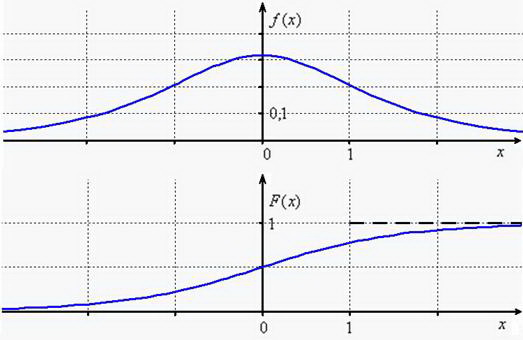
! Обратите внимание, что у 1-го графика одна, а 2-го – две горизонтальные асимптоты, «залезать» за которые нельзя!
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright