


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как вычислить площадь фигуры в полярных координатах
с помощью интеграла?
Это, пожалуй, одно из самых популярных приложений определённого интеграла после вычисления площади в прямоугольных координатах и объёма тела вращения. Для изучения материалов урока необходимо понимать, что такое полярные координаты и знать полярные уравнения простейших линий. Разумеется, потребуются навыки нахождения неопределённого и определённого интеграла, поэтому если у вас появятся технические трудности и/или недопонимание по ходу изложения, пожалуйста, начните с базовых статей.
Всё очень и очень напоминает привычную задачу нахождения площади. Полярным аналогом криволинейной трапеции является криволинейный сектор.
Рассмотрим некоторую функцию ![]() , заданную в полярной системе координат, которая принимает неотрицательные значения на отрезке
, заданную в полярной системе координат, которая принимает неотрицательные значения на отрезке ![]() и непрерывна на нём. Криволинейным сектором называется ФИГУРА, ограниченная отрезками лучей
и непрерывна на нём. Криволинейным сектором называется ФИГУРА, ограниченная отрезками лучей ![]() и графиком
и графиком ![]() :
:
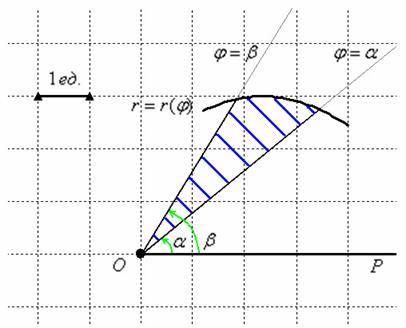
Площадь криволинейного сектора рассчитывается по формуле 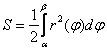 . Как видите, перед интегралом ставится дробь
. Как видите, перед интегралом ставится дробь ![]() , сама функция
, сама функция ![]() возводится в квадрат, а интегрирование осуществляется по переменной «фи».
возводится в квадрат, а интегрирование осуществляется по переменной «фи».
В качестве демонстрационного примера, вычислим площадь круга, ограниченного окружностью ![]() с центром в полюсе, радиуса 2. Очевидно, что
с центром в полюсе, радиуса 2. Очевидно, что ![]() и по формуле:
и по формуле:
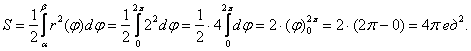
Сравните с Примером № 4 урока Эффективные методы решения определённых интегралов, где площадь этого же круга рассчитана в прямоугольной системе координат ;-)
Бензопила заправлена и прогрета:
Пример 1
Вычислить площадь фигуры, ограниченной линией ![]()
Решение: первый и главный совет:
Экономьте время на чертеже. Проще всего прибегнуть к программным средствам, например, воспользоваться моим графопостроителем в полярных координатах. Клик-клик – и готово, далее быстренько перерисовываем чертёж в тетрадь или при электронном способе оформления копируем его в Вёрд.
Если есть возможность быстро построить фигуру – всегда её стройте (даже если этого не требуется по условию). Чертёж усиливает задание, кроме того, как и при нахождении площади в прямоугольных координатах, даёт отличную возможность прикинуть по клеточкам правдоподобность получившегося результата.
Если же инструментальные средства по той или иной причине недоступны, и вы совсем не представляете, как выглядит фигура, то придерживайтесь противоположной тактики:
По возможности чертёж выгоднее НЕ строить вообще.
Ручное построение чертежа в полярных координатах – процесс длительный и трудоёмкий, за это время можно успеть выпить банку, а то и две пива решить несколько, а то и целый десяток интегралов. Исходя из личного опыта, могу с уверенностью сказать, что в простых примерах, как этот, построение чертежа на чистовике скорее не оправдано, чем оправдано. Конечно, если по условию требуется выполнить чертёж (или его дополнительно требует преподаватель), то никуда не деться, но по умолчанию гораздо рациональнее попытаться отделаться чисто аналитическим решением.
В нашем случае задача облегчается ещё и тем, что ![]() для любого «фи»,
для любого «фи»,
а значит, угол, как и в примере с площадью круга, принимает все значения от ![]() до
до ![]() . По рабочей формуле:
. По рабочей формуле:
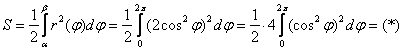
Стандартно понижаем степень с помощью известной тригонометрической формулы:

Ничего сложного тут нет, главное, не допустить ошибку в преобразованиях и вычислениях.
В частности, не забывайте, что площадь не может быть отрицательной, и если у вас вдруг получится такой результат, ищите оплошность.
Ответ: ![]()
Забавно, что можно вообще не иметь ни малейшего представления о том, какую фигуру ограничивает линия ![]() . Однако студенческое счастье переменчиво и всегда нужно быть готовым к худшему сценарию:
. Однако студенческое счастье переменчиво и всегда нужно быть готовым к худшему сценарию:
Как построить фигуру, если её НАДО построить, но под рукой нет программы?
Не унываем, схематический чертёж отнимет не так уж много времени. Такой версии, скорее всего, будет достаточно, ведь это не главная часть задания.
В который раз взглянем на график косинуса:
на интервале ![]() косинус принимает такие же по модулю значения, что и на интервале
косинус принимает такие же по модулю значения, что и на интервале ![]() , только со знаком «минус». Поскольку у нас косинус возводится в квадрат, то фигура, ограниченная графиком функции
, только со знаком «минус». Поскольку у нас косинус возводится в квадрат, то фигура, ограниченная графиком функции ![]() , будет состоять из двух одинаковых и симметричных относительно полюса частей, вершины которых, очевидно, находятся в следующих точках:
, будет состоять из двух одинаковых и симметричных относительно полюса частей, вершины которых, очевидно, находятся в следующих точках:
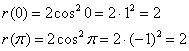
Так же очевидно, что при ![]() полярный радиус равен нулю.
полярный радиус равен нулю.
Давайте найдём дополнительную опорную точку. Напрашивается угол в 45 градусов:
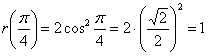
В силу симметрии линии: ![]()
Как называется эта фигура, я не знаю, …сейчас немного проанализировал, …какая-то алгебраическая кривая 6-го порядка:
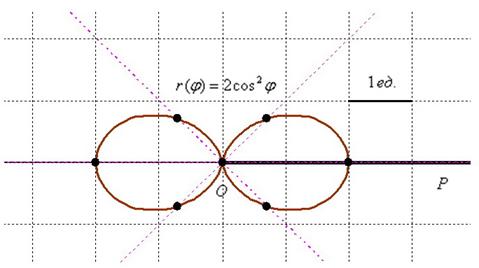
По ходу пьесы всячески приветствуется импровизация, так, в данном примере уместно найти значение ![]() для более точного построения чертежа.
для более точного построения чертежа.
Ну и, конечно же, не забываем по клеточкам оценить, что полученное значение площади ![]() похоже на правду.
похоже на правду.
Пример 2
Вычислить площадь фигуры, ограниченной линией ![]()
Это пример для самостоятельного решения. Примерный образец чистового оформления задачи в конце урока.
Если на пути встаёт область определения, то блицкриг тоже вполне осуществим:
Пример 3
Вычислить площадь фигуры, ограниченной линией ![]()
Решение: данное уравнение задаёт двухлепестковую полярную розу, область определения: ![]() . Лепестки одинаковы, поэтому достаточно найти площадь одного из них, а результат удвоить. Удваивать рекомендую сразу же (в конце задания забывается просто «на ура»):
. Лепестки одинаковы, поэтому достаточно найти площадь одного из них, а результат удвоить. Удваивать рекомендую сразу же (в конце задания забывается просто «на ура»):

(*) На данном шаге использовали чётность подынтегральной функции на симметричном относительно нуля отрезке интегрирования. С геометрической точки зрения это означает, что лепесток розы симметричен относительно своей центральной оси. В предыдущих двух примерах фигуры тоже были симметричными, но, как ни странно, в рассматриваемом типе задач излишнее обмусоливание данного факта зачастую только удлиняет решение.
Ответ: ![]()
Если считать, что уравнение ![]() задано в обобщенных полярных координатах, то данная роза будет иметь 4 лепестка, и, соответственно, результат следует умножить ещё на два. Но, как я уже советовал в курсе аналитической геометрии, осмотрительнее рассматривать классику, где полярный радиус неотрицателен.
задано в обобщенных полярных координатах, то данная роза будет иметь 4 лепестка, и, соответственно, результат следует умножить ещё на два. Но, как я уже советовал в курсе аналитической геометрии, осмотрительнее рассматривать классику, где полярный радиус неотрицателен.
Следующие короткие задачи предназначены для самостоятельного решения:
Пример 4
Вычислить площадь фигуры, ограниченной линией, заданной уравнением ![]() в полярной системе координат.
в полярной системе координат.
Пример 5
Вычислить площадь фигуры, ограниченной линией, заданной уравнением ![]() в полярной системе координат.
в полярной системе координат.
Кривая 4-го примера называется лемнискатой Бернулли, в 5-м примере дана трёхлепесковая роза. Напоминаю, что если есть возможность быстро построить чертеж, то его лучше построить. А здесь они, к слову, быстро строятся и вручную.
После интенсивной разминки на опушке надеваем хоккейную маску и с воодушевлением углубляемся в лес за новыми жертвами:
Пример 6
Вычислить площадь фигуры, ограниченной линиями ![]() .
.
Решение: в условии даны две линии, и здесь хоть о чертеже и молчок, но без него уже трудно. Какую кривую задаёт уравнение ![]() ? В статье о полярных координатах мы подробно разбирали и строили график полярной розы
? В статье о полярных координатах мы подробно разбирали и строили график полярной розы ![]() с лепестками на промежутках
с лепестками на промежутках ![]() . Знак «минус» всё перевернёт с ног на голову (а если академичнее – отобразит симметрично относительно полярной оси и её продолжения) и лепестки розы
. Знак «минус» всё перевернёт с ног на голову (а если академичнее – отобразит симметрично относительно полярной оси и её продолжения) и лепестки розы ![]() расположатся в секторах
расположатся в секторах ![]() .
.
Уравнение же ![]() значительно проще, оно определяет типовую окружность:
значительно проще, оно определяет типовую окружность:
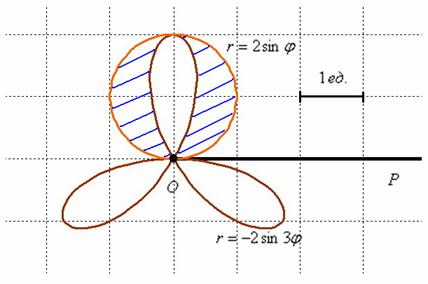
Искомая фигура заштрихована синим цветом. Чтобы вычислить её площадь, нужно из площади круга вычесть площадь одного лепестка розы.
1) Вычислим площадь круга. Пределы интегрирования ![]() , по формуле:
, по формуле:
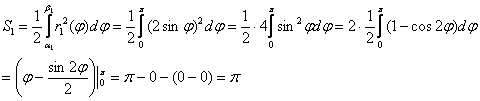
Результат, не забываем, легко проверяется с помощью школьной формулы.
2) Вычислим площадь лепестка розы, расположенного в пределах ![]() :
:
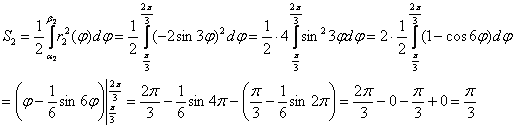
3) Площадь искомой фигуры:
![]() … математический каламбур прямо какой-то =)
… математический каламбур прямо какой-то =)
Ответ: ![]() , что весьма правдоподобно
, что весьма правдоподобно
В рассмотренном примере фигурировали разные отрезки интегрирования, и площадь выразилась разностью 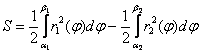 . Однако на практике данные промежутки чаще совпадают и по причине линейности интеграла формула упрощается. Сформулирую правило в общем виде: если функции
. Однако на практике данные промежутки чаще совпадают и по причине линейности интеграла формула упрощается. Сформулирую правило в общем виде: если функции ![]() непрерывны и неотрицательны на некотором отрезке
непрерывны и неотрицательны на некотором отрезке ![]() , и при этом
, и при этом ![]() , то площадь фигуры, ограниченной отрезками лучей
, то площадь фигуры, ограниченной отрезками лучей ![]() и данными линиями, равна:
и данными линиями, равна:
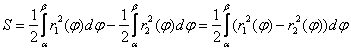
Нетрудно уловить, что общий мотив похож на вычисление площади в прямоугольных координатах по формуле 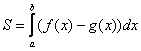 , где из «верхней» функции, вычитается «нижняя».
, где из «верхней» функции, вычитается «нижняя».
Следующий баян лучше не пропускать:
Пример 7
Вычислить площадь фигуры, ограниченной линиями ![]() .
.
Краткое решение с чертёжом в конце урока.
И в заключение ещё одна распространённая разновидность задачи, после чего будет специальное предложение для самых увлечённых маньяков:
Пример 8
Вычислить площадь фигуры, ограниченной линиями, заданными в полярных координатах
![]() .
.
Решение: с художеством особых проблем не возникает, однако фигура, ограниченная окружностями ![]() , не определена однозначно и поэтому в условии наложено дополнительное ограничение на угол
, не определена однозначно и поэтому в условии наложено дополнительное ограничение на угол ![]() , из которого следует, что необходимо вычислить заштрихованную площадь:
, из которого следует, что необходимо вычислить заштрихованную площадь:
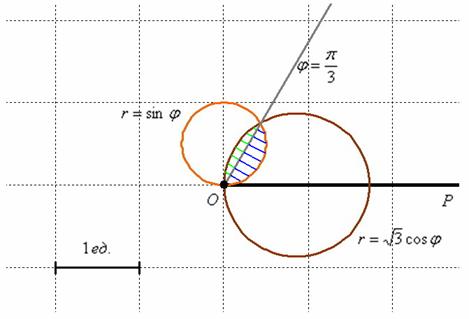
Сначала разберёмся, как найти луч ![]() , по которому пересекаются окружности. Очень просто – приравниваем функции и решаем уравнение:
, по которому пересекаются окружности. Очень просто – приравниваем функции и решаем уравнение:
![]()
Сбрасываем косинус на нижний ярус левой части и превращаем дробь в тангенс:
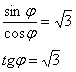
Таким образом: ![]()
Из чертежа следует, что площадь фигуры нужно искать как сумму площадей:
1) На промежутке ![]() фигура ограничена отрезком луча
фигура ограничена отрезком луча ![]() и дугой окружности (внимание!!)
и дугой окружности (внимание!!) ![]() (синяя штриховка).
(синяя штриховка).

2) На промежутке ![]() фигура ограничена тем же отрезком луча
фигура ограничена тем же отрезком луча ![]() и дугой окружности
и дугой окружности ![]() (зелёная штриховка).
(зелёная штриховка).

Интегралы настоятельно рекомендую считать РАЗДЕЛЬНО – риск допустить ошибку по невнимательности как никогда велик. Только что ещё раз убедился на собственном опыте, пытаясь оформить решение «одной строкой».
3) А вот теперь пользуемся аддитивностью площади:
![]()
Ответ: ![]()
Аналогичное задание для самостоятельного решения:
Пример 9
Вычислить площадь фигуры, ограниченной линиями, заданными в полярных координатах
![]() . Выполнить чертёж.
. Выполнить чертёж.
Заметьте, что условие данной задачи требует выполнения чертёжа (даже если Вы с ходу представили, как выглядит фигура и даже если мысленно всё рассчитали). Всегда обращайте внимание на формулировку. Примерный образец решения совсем близко.
Надо сказать, что я разобрал не самые сложные задания, дабы не отпугнуть «чайников». Дополнительные примеры можно найти в решебнике Л. А. Кузнецова (Раздел IV - Интегралы, Задача 16). Но таки приберегите немного сил на вычисление площадей фигур, ограниченных параметрически заданными линиями =)
И удачи вам в пятницу тринадцатого!
Решения и ответы:
Пример 2: Решение: найдём область определения: ![]() – любое.
– любое.
Площадь фигуры вычислим по формуле 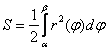 , в данном случае
, в данном случае ![]() :
:
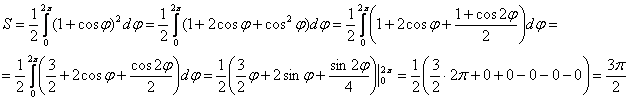
Ответ: ![]()
Примечание: линия, которой ограничена данная фигура, называется кардиоидой, чертёж можно посмотреть в Примере № 6 урока Как построить график в полярной системе координат?
Пример 4: Решение: область определения: ![]() . Фигура состоит из двух одинаковых частей. Используя формулу
. Фигура состоит из двух одинаковых частей. Используя формулу 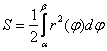 , вычислим площадь на отрезке
, вычислим площадь на отрезке ![]() , результат удвоим:
, результат удвоим:
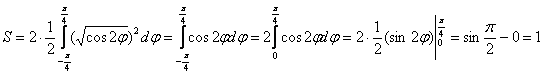
Ответ: ![]()
Пример 5: Решение: данное уравнение задаёт трёхлепестковую розу, область определения:
![]()
Используя формулу 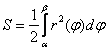 , вычислим площадь фигуры на отрезке
, вычислим площадь фигуры на отрезке ![]() , результат утроим:
, результат утроим:

Ответ: ![]()
Пример 7: Решение: выполним чертёж:
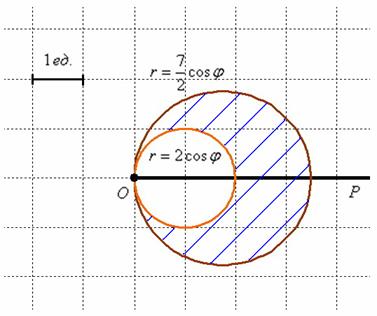
На отрезке ![]() , таким образом:
, таким образом:
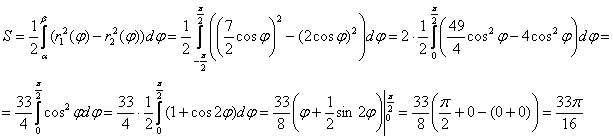
Ответ: ![]()
Пример 9: Решение: найдём угловое направление пересечения окружностей:
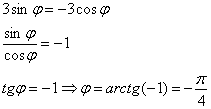
По условию ![]() , поэтому рассматриваем противоположнонаправленный луч
, поэтому рассматриваем противоположнонаправленный луч ![]() . Выполним чертёж:
. Выполним чертёж:
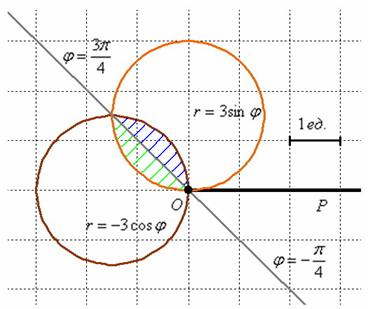
1) На промежутке ![]() фигура ограничена отрезком луча
фигура ограничена отрезком луча ![]() и дугой окружности
и дугой окружности ![]() .
.
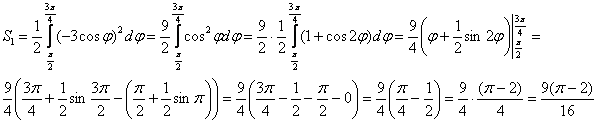
2) На промежутке ![]() фигура ограничена отрезком луча
фигура ограничена отрезком луча ![]() и дугой окружности
и дугой окружности ![]() .
.

3) Площадь фигуры:
![]()
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright