Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Решение системы при различных способах выбора базиса

Представляю вашему вниманию заключительную статью по теме решения систем линейных уравнений. Материал предназначен для читателей, владеющих техникой элементарных преобразований на среднем и высоком уровне. Чайникам рекомендую начать с урока метод Гаусса для чайников =), ну а остальным, как людям опытным, предлагаю непосредственно перейти к обсуждению задачи.

Рассмотрим некоторую систему линейных уравнений с пятью неизвестными . Можно было взять мЕньшее количество переменных, можно бОльшее, суть не в этом. Предположим, данная система совместна и имеет общее решение, в котором базисные переменные  выражаются через свободные переменные .

Ответим на вопрос, который зародился ещё на уроке Несовместные системы/системы с общим решением и окончательно созрел к занятию Метод Гаусса-Жордана:

А почему, собственно, в роли базисных переменных должны выступать именно ? Нельзя ли в качестве базиса выбрать, например, набор ? Действительно, чем хуже «обычных» ? 

Примечание: здесь и далее термин «базис» используется в общем алгебраическом смысле, пожалуйста, не ассоциируйте его с аффинным базисом плоскости или пространства.

В данном примере любые три переменные из списка  могут выступать в качестве базисных переменных.

И сегодня мы узнаем, как находить решение системы в различных базисах:

Пример 1

Исследовать систему линейных уравнений на совместность. В случае совместности найти её решение при различных способах выбора базиса.

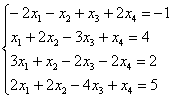
Решение: надо сказать, задачка не внушает оптимизма, велика вероятность, что система совместна и нам придётся ворочать базисы. Ещё бы – вряд ли в таком контексте условия студент отделается несовместностью системы или единственным решением =)

Но, так или иначе, первая часть предполагает исследование на совместность, которое проводится по типовой схеме с использованием теоремы Кронекера-Капелли. Спросите, зачем тут втиснулось исследование? Я взял пример из конкретной контрольной работы и решил не убирать первую часть (хотя мог бы), поскольку реализм на данном сайте ценится очень высоко.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

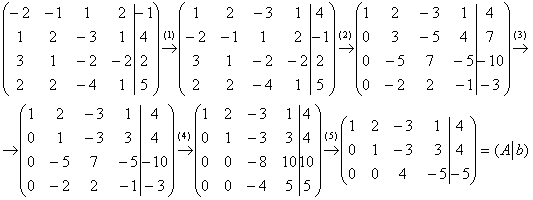
(1) Первую и вторую строки поменяли местами.

(2) Ко второй, третьей, четвертой строкам прибавили первую строку, умноженную на 2, –3 и –2 соответственно.

(3) Ко второй строке прибавили четвертую строку.

(4) К третьей и четвертой строкам прибавили вторую строку, умноженную на 5 и 2 соответственно.

(5) Третья и четвертая строки пропорциональны, третью строку удаляем. У последней строки меняем знак.

Если не очень понятны какие-нибудь моменты в преобразованиях, то, пожалуйста, отработайте метод Гаусса, благо, примеров я разобрал достаточно много.

Проверка системы на совместность оформляется по шаблону, рассмотренному в последнем параграфе статьи о ранге матрицы:

В результате элементарных преобразований получены эквивалентная исходным матрица системы  и расширенная матрица системы .

Максимальный порядок ненулевого минора матрицы системы равен 3, например 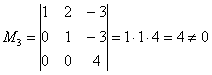, следовательно, .

По этой же причине .

Вывод: , значит, по теореме Кронекера-Капелли  система совместна.

Элементарные образования приблизили нас к наиболее традиционному выбору:
 – базисные переменные;
 – свободная переменная.

Обратный ход метода Гаусса работает без всяких чудес. Из третьего уравнения:
 – подставим во второе уравнение:

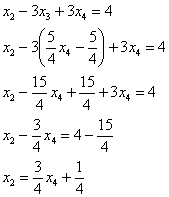
Подставим  и  в первое уравнение:

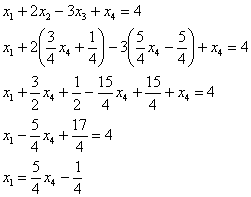
Общее решение системы в базисе  можно записать в привычном виде , но в целях выполнения дальнейших действий его удобнее оформить так:

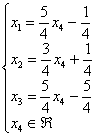
Запись  обозначает, что свободная переменная принимает произвольные действительные значения, порождая тем самым бесконечно много частных решений.

Выполним стандартную проверку – подставим результат в левую часть каждого уравнения исходной системы:

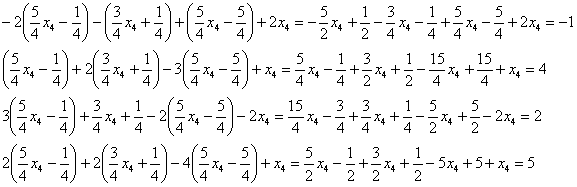
Получены правые части соответствующих уравнений, таким образом, общее решение найдено верно. Саму систему лучше переписать в тетрадь или распечатать – чтобы посматривать на неё в ходе последующих проверок.

По условию задачи требуется найти решение системы при различных (читай – при всех!) способах выбора базисных переменных. Помимо набора  возможны следующие варианты:

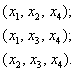
Других сочетаний нет.

Не сказать, что задание сильно короткое, но с другой стороны в депрессию тоже не загонит. Начинаем путешествие:

В построенном базисе  переведём неизвестную  в разряд свободных
( соответственно станет базисной). Переменная  содержится в третьей строке полученного решения 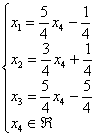, поэтому нужно взять эту строку и выразить  через :

Подставим  в оставшиеся выражения:

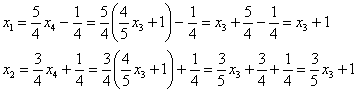
И, соблюдая порядок переменных, запишем решение системы в базисе

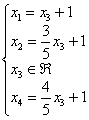
Для самоконтроля удостоверимся, что в правых частях находятся только свободные переменные (в нашем случае ) и константы. Запись  обозначает, что свободная переменная принимает произвольные действительные значения.

Общее решение также можно оформить и в обычном виде:
.

Понимаю, что неохота, но проходим таможенный контроль:

Проверка: подставим найдённое решение в левую часть каждого уравнения системы:

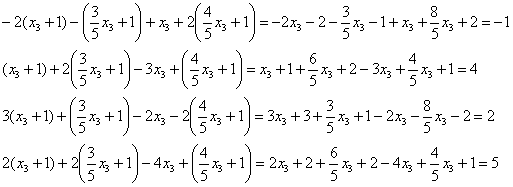
Получены соответствующие правые части уравнений, что и требовалось проверить.

Осуществим переход к следующему базисному решению:

Поскольку переменная  становится свободной, то из второй строчки текущего решения 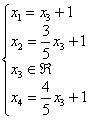 нужно выразить:

 – и подставить в оставшиеся выражения (первую и четвертую строки):

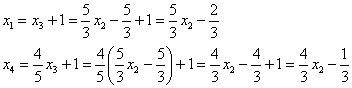
Таким образом, решение системы в базисе :

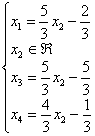
И снова окидываем результат взглядом – справа у нас должна находиться только свободная переменная  и константы.

Проверка: подставим результат в левую часть каждого уравнения системы:

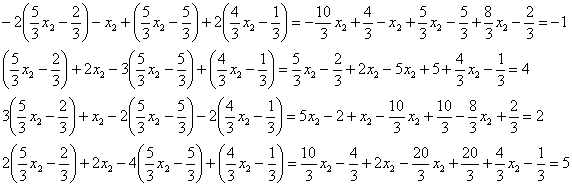
Получены правые части соответствующих уравнений, значит, решение найдено верно.

Каждый раз проверку, конечно, можете и не выполнять, но тут есть одно большое и жирное НО В рассматриваемом задании часто ошибаются по невнимательности, поэтому настоятельно рекомендую проверять решение на каждом шаге – ведь если пропустить ошибку, всё остальное тоже будет неправильно. Ещё одним аргументом выступает сам естественнонаучный принцип: любое утверждение должно быть обосновано и/или доказано. Проверка реальна? Обязательно проверяем! Кстати, не такой плохой принцип и во многих жизненных ситуациях.

Завершая задание, найдём решение системы в 4-м базисе. Осуществим переход:

Переменные  и  меняются ролями, а значит, из первой строки текущего решения 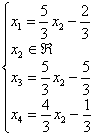 следует выразить:

 – подставим в оставшиеся выражения (3-ю и 4-ю строки):

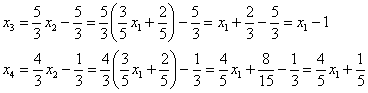
Записываем общее решение системы в базисе :

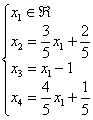
Проверка: подставим найденное  решение в левую часть каждого уравнения системы:

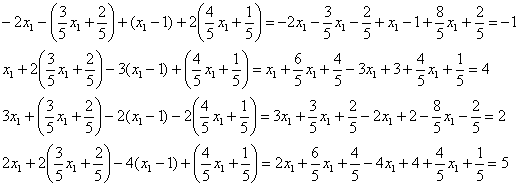
ОК.

Желающие могут замкнуть кругосветный круиз переходом , получив тем самым первоначальное решение.

В соответствии с условием задачи оформляем резюме:

Ответ: система совместна, решение системы при различных способах выбора базиса: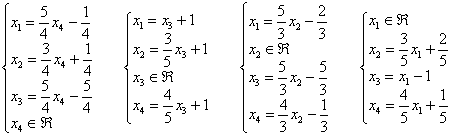

Если в системе с четырьмя неизвестными  базис состоит из двух переменных (например,  – базисные переменные,  – свободные переменные), то переход от одного решения к другому решению следует осуществлять по тому же алгоритму, и он даже запишется несколько компактнее, чем в разобранной задаче. Правда, самих базисов будет больше:

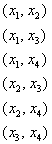
Количество базисов системы с  переменными,  из которых образуют базис, можно подсчитать с помощью комбинаторной формулы количества сочетаний .

Так, в условном примере начала урока с системой, содержащей  пять неизвестных , три из которых образуют базис, будет уже 10 различных базисных решений.

Однако на практике я не встречал ни того, ни другого случая, видимо, связка 4 переменные – 3 базисные переменные является наиболее разумной с точки зрения объёма работы.

Такое тоже не встречалось, но на всякий пожарный: что делать, если по условию требуется найти конкретный базис, например, решение с базисными переменными  и свободной переменной ?

При необходимости найти этот базис сразу выручит только метод Гаусса-Жордана, и ваша цель – привести расширенную матрицу системы к виду 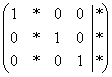. Если же автор задачи не торопит вас с ответом, то кроме первого способа, годится и второй, более длинный путь: получаем «традиционное» решение и «без посредников» осуществляем переход к нужному базису: .

Очевидно, что путешествовать от базиса к базису можно по разным маршрутам и решение следующей системы служит наглядной иллюстрацией данного факта:

Пример 2

Найти решение системы линейных уравнений при различных способах выбора базиса

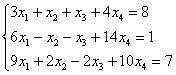
В образце первое базисное решение получено методом Гаусса-Жордана, который здесь более выгоден, чем обратный ход метода Гаусса. 

В предложенной системе перебор базисных решений проведён в следующем порядке:

Более стандартна последовательность первого примера, но данный вопрос не принципиален, и для закрепления алгоритма рекомендую попытаться провести решение по альтернативному маршруту, который Птицей счастья завтрашнего дня появляется на экранах ваших мониторов.

Постарайтесь выполнить задание самостоятельно!

Решение: запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

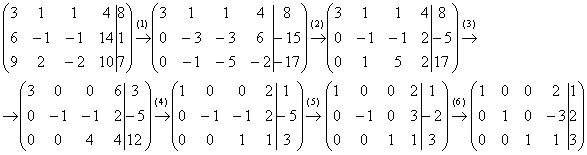
 (1) Ко второй и третьей строкам прибавили первую строку, умноженную на –2 и –3 соответственно.
(2) Вторую строку разделили на 3, у третьей строки сменили знак.
(3) К первой и третьей строкам прибавили вторую строку.
(4) Первую строку разделили на 3, третью строку разделили на 4.
(5) Ко второй строке прибавили третью строку
(6) У второй строки сменили знак.
Таким образом, решение системы в базисе :

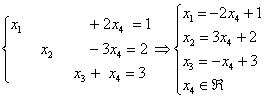
Проверка: подставим данное решение в левую часть каждого уравнения системы:

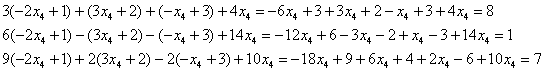
Получены правые части соответствующих уравнений, что и требовалось проверить.

Найдем решение в базисе . Переменная  переходит в разряд свободных, поэтому из первой строки текущего решения выразим:
 – подставим во вторую и третью строки:

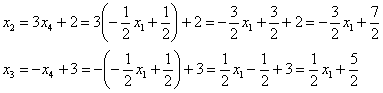
В результате, решение в базисе :

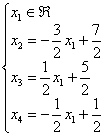
Проверка: подставим данное решение в левую часть каждого уравнения системы:

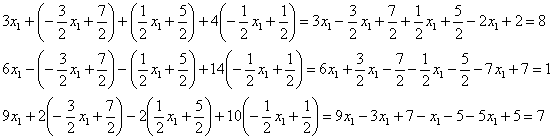
Получены правые части соответствующих уравнений, значит, решение найдено правильно.

Осуществим переход к базису . Переменная  перейдёт в разряд свободных, поэтому из 2-й строки текущего решения выразим:
 – подставим в третью и четвертую строки:

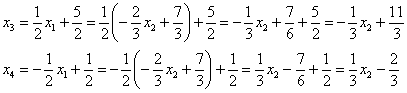
Таким образом, решение в базисе :

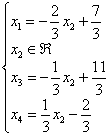
Проверка: Подставим данное решение в левую часть каждого уравнения системы:
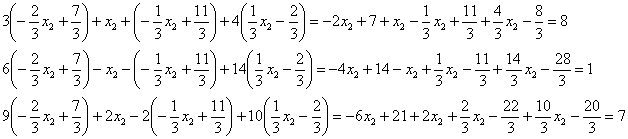Найденное решение удовлетворяет каждому уравнению системы.

Перейдём к базису . Переменная  уходит в разряд свободных, поэтому из 3-й строки текущего решения выразим:
 – подставим в 1-ю и 4-ю строки:

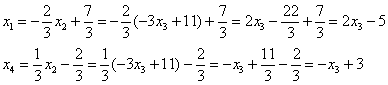
Решение в базисе :

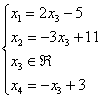
Проверка: Подставим данное решение в левую часть каждого уравнения системы:

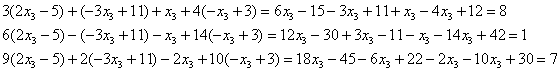
Полученное  решение удовлетворяет каждому уравнению системы.

Ответ: решение системы при различных способах выбора базиса:

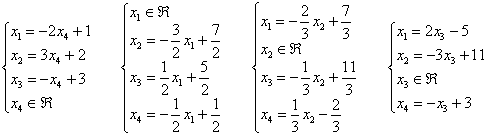
Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте