


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Интегрирование дробно-рациональной функции.
Метод неопределенных коэффициентов
Продолжаем заниматься интегрированием дробей. Интегралы от некоторых видов дробей мы уже рассмотрели на уроке Интегрирование некоторых дробей, и этот урок в некотором смысле можно считать продолжением. Для успешного понимания материала необходимы базовые навыки интегрирования, поэтому если Вы только приступили к изучению интегралов, то есть являетесь чайником, то следует начать со статьи Неопределенный интеграл. Примеры решений.
Как ни странно, сейчас мы будем заниматься не столько нахождением интегралов, сколько… решением систем линейных уравнений. В этой связи настоятельно рекомендую посетить урок Как решить систему линейных уравнений? А именно – нужно хорошо ориентироваться в методах подстановки («школьном» методе и методе почленного сложения (вычитания) уравнений системы).
Что такое дробно-рациональная функция? Простыми словами, дробно-рациональная функция – это дробь, в числителе и знаменателе которой находятся многочлены либо произведения многочленов. При этом дроби являются более навороченными, нежели те, о которых шла речь в статье Интегрирование некоторых дробей.
Интегрирование правильной дробно-рациональной функции
Сразу пример и типовой алгоритм решения интеграла от дробно-рациональной функции.
Пример 1
Найти неопределенный интеграл.
![]()
Шаг 1. Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной? Данный шаг выполняется устно, и сейчас я объясню как:
Сначала смотрим на числитель и выясняем старшую степень многочлена:
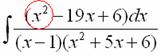
Старшая степень числителя равна двум.
Теперь смотрим на знаменатель и выясняем старшую степень знаменателя. Напрашивающийся путь – это раскрыть скобки и привести подобные слагаемые, но можно поступить проще, в каждой скобке находим старшую степень
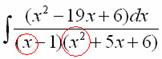
и мысленно умножаем: ![]() – таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх.
– таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх.
Вывод: старшая степень числителя СТРОГО меньше старшей степени знаменателя, значит, дробь является правильной.
Если бы в данном примере в числителе находился многочлен 3, 4, 5 и т. д. степени, то дробь была бы неправильной.
Сейчас мы будем рассматривать только правильные дробно-рациональные функции. Случай, когда степень числителя больше либо равна степени знаменателя, разберём в конце урока.
Шаг 2. Разложим знаменатель на множители. Смотрим на наш знаменатель:
![]()
Вообще говоря, здесь уже произведение множителей, но, тем не менее, задаемся вопросом: нельзя ли что-нибудь разложить еще? Объектом пыток, несомненно, выступит квадратный трехчлен. Решаем квадратное уравнение:
![]()
Дискриминант больше нуля, значит, трехчлен действительно раскладывается на множители:
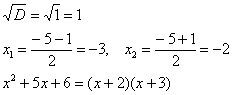
Общее правило: ВСЁ, что в знаменателе МОЖНО разложить на множители – раскладываем на множители
Начинаем оформлять решение:
![]()
Шаг 3. Методом неопределенных коэффициентов раскладываем подынтегральную функцию в сумму простых (элементарных) дробей. Сейчас будет понятнее.
Смотрим на нашу подынтегральную функцию:
![]()
И, знаете, как-то проскакивает интуитивная мысль, что неплохо бы нашу большую дробь превратить в несколько маленьких. Например, вот так:
![]()
Возникает вопрос, а можно ли вообще так сделать? Вздохнем с облегчением, соответствующая теорема математического анализа утверждает – МОЖНО. Такое разложение существует и единственно.
Только есть одна загвоздочка, коэффициенты ![]() мы пока не знаем, отсюда и название – метод неопределенных коэффициентов.
мы пока не знаем, отсюда и название – метод неопределенных коэффициентов.
Как вы догадались, последующие телодвижения так, не гоготать! будут направлены на то, чтобы как раз их УЗНАТЬ – выяснить, чему же равны ![]() .
.
Будьте внимательны, подробно объясняю один раз!
Итак, начинаем плясать от:
![]()
В левой части приводим выражение к общему знаменателю:
![]()
Теперь благополучно избавляемся от знаменателей (т. к. они одинаковы):
![]()
В левой части раскрываем скобки, неизвестные коэффициенты ![]() при этом пока не трогаем:
при этом пока не трогаем:
![]()
Заодно повторяем школьное правило умножения многочленов. В свою бытность учителем, я научился выговаривать это правило с каменным лицом: Для того чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
С точки зрения понятного объяснения коэффициенты ![]() лучше внести в скобки (хотя лично я никогда этого не делаю в целях экономии времени):
лучше внести в скобки (хотя лично я никогда этого не делаю в целях экономии времени):
![]()
Составляем систему линейных уравнений.
Сначала разыскиваем старшие степени:
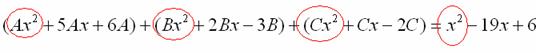
И записываем соответствующие коэффициенты в первое уравнение системы:
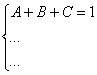
Хорошо запомните следующий нюанс. Что было бы, если б в правой части вообще не было ![]() ? Скажем, красовалось бы просто
? Скажем, красовалось бы просто ![]() без всякого квадрата? В этом случае в уравнении системы нужно было бы поставить справа ноль:
без всякого квадрата? В этом случае в уравнении системы нужно было бы поставить справа ноль: ![]() . Почему ноль? А потому что в правой части всегда можно приписать этот самый квадрат с нулём:
. Почему ноль? А потому что в правой части всегда можно приписать этот самый квадрат с нулём: ![]() Если в правой части отсутствуют какие-нибудь переменные или (и) свободный член, то в правых частях соответствующих уравнений системы ставим нули.
Если в правой части отсутствуют какие-нибудь переменные или (и) свободный член, то в правых частях соответствующих уравнений системы ставим нули.
Далее процесс идет по снижающейся траектории, от водки к пиву, отмечаем все «иксы»:
![]()
Записываем соответствующие коэффициенты во второе уравнение системы:
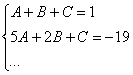
И, наконец, минералка, подбираем свободные члены.
Эх,…что-то я расшутился. Шутки прочь – математика наука серьезная. У нас в институтской группе никто не смеялся, когда доцент сказала, что разбросает члены по числовой прямой и выберет из них самые большие. Настраиваемся на серьезный лад. Хотя… кто доживет до конца этого урока, все равно будет тихо улыбаться.
![]()
Система готова:
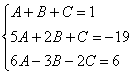
Решаем систему:
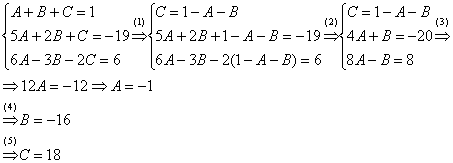
(1) Из первого уравнения выражаем ![]() и подставляем его во 2-е и 3-е уравнения системы. На самом деле можно было выразить
и подставляем его во 2-е и 3-е уравнения системы. На самом деле можно было выразить ![]() (или другую букву) из другого уравнения, но в данном случае выгодно выразить именно из 1-го уравнения, поскольку там самые маленькие коэффициенты.
(или другую букву) из другого уравнения, но в данном случае выгодно выразить именно из 1-го уравнения, поскольку там самые маленькие коэффициенты.
(2) Приводим подобные слагаемые во 2-м и 3-м уравнениях.
(3) Почленно складываем 2-е и 3-е уравнение, при этом, получая равенство ![]() , из которого следует, что
, из которого следует, что ![]()
(4) Подставляем ![]() во второе (или третье) уравнение, откуда находим, что
во второе (или третье) уравнение, откуда находим, что ![]()
(5) Подставляем ![]() и
и ![]() в первое уравнение, получая
в первое уравнение, получая ![]() .
.
Если возникли трудности с методами решения системы отработайте их на уроке Как решить систему линейных уравнений?
После решения системы всегда полезно сделать проверку – подставить найденные значения ![]() в каждое уравнение системы, в результате всё должно «сойтись».
в каждое уравнение системы, в результате всё должно «сойтись».
Почти приехали. Коэффициенты ![]() найдены, при этом:
найдены, при этом:
![]()
Чистовое оформление задание должно выглядеть примерно так:
![]()
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
![]()
![]()
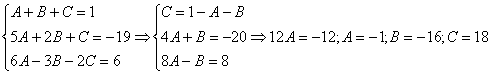

Как видите, основная трудность задания состояла в том, чтобы составить (правильно!) и решить (правильно!) систему линейных уравнений. А на завершающем этапе всё не так сложно: используем свойства линейности неопределенного интеграла и интегрируем. Обращаю внимание, что под каждым из трёх интегралов у нас «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле.
Проверка. Дифференцируем ответ:
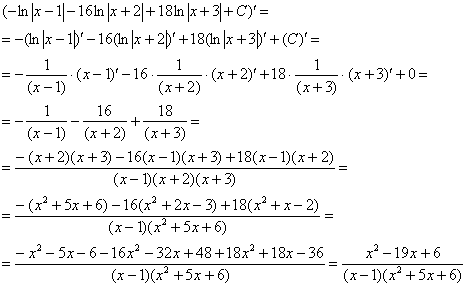
Получена исходная подынтегральная функция, значит, интеграл найден правильно.
В ходе проверки пришлось приводить выражение к общему знаменателю, и это не случайно. Метод неопределенных коэффициентов и приведение выражения к общему знаменателю – это взаимно обратные действия.
Пример 2
Найти неопределенный интеграл.
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Вернемся к дроби из первого примера: ![]() . Нетрудно заметить, что в знаменателе все множители однотипные. Возникает вопрос, а что делать, если дана, например, такая дробь:
. Нетрудно заметить, что в знаменателе все множители однотипные. Возникает вопрос, а что делать, если дана, например, такая дробь: ![]() ? Здесь в знаменателе у нас степени, или, по-математически кратные множители. Кроме того, есть неразложимый на множители квадратный трехчлен
? Здесь в знаменателе у нас степени, или, по-математически кратные множители. Кроме того, есть неразложимый на множители квадратный трехчлен ![]() (легко убедиться, что дискриминант уравнения
(легко убедиться, что дискриминант уравнения ![]() отрицателен, поэтому на множители трехчлен никак не разложить). Что делать? Разложение в сумму элементарных дробей будет выглядеть наподобие
отрицателен, поэтому на множители трехчлен никак не разложить). Что делать? Разложение в сумму элементарных дробей будет выглядеть наподобие ![]() с неизвестными коэффициентами
с неизвестными коэффициентами ![]() вверху или как-то по-другому?
вверху или как-то по-другому?
Пример 3
Представить функцию ![]() в виде суммы элементарных дробей с неизвестными коэффициентами.
в виде суммы элементарных дробей с неизвестными коэффициентами.
Шаг 1. Проверяем, правильная ли у нас дробь
Старшая степень числителя: 2
Старшая степень знаменателя: 8
![]() , значит, дробь является правильной.
, значит, дробь является правильной.
Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Очевидно, что нет, всё уже разложено. Квадратный трехчлен ![]() не раскладывается в произведение по указанным выше причинам. Гуд. Работы меньше.
не раскладывается в произведение по указанным выше причинам. Гуд. Работы меньше.
Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей.
В данном случае, разложение имеет следующий вид:
![]()
Смотрим на наш знаменатель: ![]()
При разложении дробно-рациональной функции в сумму элементарных дробей можно выделить три принципиальных момента:
1) Если в знаменателе находится «одинокий» множитель в первой степени (в нашем случае ![]() ), то вверху ставим неопределенный коэффициент (в нашем случае
), то вверху ставим неопределенный коэффициент (в нашем случае ![]() ). Примеры 1, 2 состояли только из таких «одиноких» множителей.
). Примеры 1, 2 состояли только из таких «одиноких» множителей.
2) Если в знаменателе есть кратный множитель ![]() , то раскладывать нужно так:
, то раскладывать нужно так:
![]() – то есть последовательно перебрать все степени «икса» от первой до энной степени. В нашем примере два кратных множителя:
– то есть последовательно перебрать все степени «икса» от первой до энной степени. В нашем примере два кратных множителя: ![]() и
и ![]() , еще раз взгляните на приведенное мной разложение и убедитесь, что они разложены именно по этому правилу.
, еще раз взгляните на приведенное мной разложение и убедитесь, что они разложены именно по этому правилу.
3) Если в знаменателе находится неразложимый многочлен второй степени (в нашем случае ![]() ), то при разложении в числителе нужно записать линейную функцию с неопределенными коэффициентами (в нашем случае
), то при разложении в числителе нужно записать линейную функцию с неопределенными коэффициентами (в нашем случае ![]() с неопределенными коэффициентами
с неопределенными коэффициентами ![]() и
и ![]() ).
).
На самом деле, есть еще 4-й случай, но о нём я умолчу, поскольку на практике он встречается крайне редко.
Пример 4
Представить функцию ![]() в виде суммы элементарных дробей с неизвестными коэффициентами.
в виде суммы элементарных дробей с неизвестными коэффициентами.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Строго следуйте алгоритму!
Если Вы разобрались, по каким принципам нужно раскладывать дробно-рациональную функцию в сумму, то сможете разгрызть практически любой интеграл рассматриваемого типа.
Пример 5
Найти неопределенный интеграл.
![]()
Шаг 1. Очевидно, что дробь является правильной: ![]()
Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Можно. Здесь сумма кубов ![]() . Раскладываем знаменатель на множители, используя формулу сокращенного умножения
. Раскладываем знаменатель на множители, используя формулу сокращенного умножения ![]()
![]()
Шаг 3. Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
Обратите внимание, что многочлен ![]() неразложим на множители (проверьте, что дискриминант отрицательный), поэтому вверху мы ставим линейную функцию
неразложим на множители (проверьте, что дискриминант отрицательный), поэтому вверху мы ставим линейную функцию ![]() с неизвестными коэффициентами, а не просто одну буковку.
с неизвестными коэффициентами, а не просто одну буковку.
Приводим дробь к общему знаменателю:
![]()
![]()
Составим и решим систему:
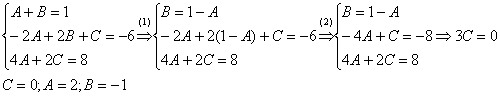
(1) Из первого уравнения выражаем ![]() и подставляем во второе уравнение системы (это наиболее рациональный способ).
и подставляем во второе уравнение системы (это наиболее рациональный способ).
(2) Приводим подобные слагаемые во втором уравнении.
(3) Почленно складываем второе и третье уравнения системы.
Все дальнейшие расчеты, в принципе, устные, так как система несложная.
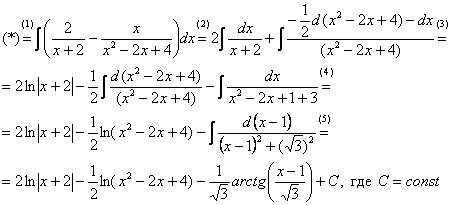
(1) Записываем сумму дробей в соответствии с найденными коэффициентами ![]() .
.
(2) Используем свойства линейности неопределенного интеграла. Что произошло во втором интеграле? С этим методом Вы можете ознакомиться в последнем параграфе урока Интегрирование некоторых дробей.
(3) Еще раз используем свойства линейности. В третьем интеграле начинаем выделять полный квадрат (предпоследний параграф урока Интегрирование некоторых дробей).
(4) Берём второй интеграл, в третьем – выделяем полный квадрат.
(5) Берём третий интеграл. Готово.
А вот вам еще пара примеров для самостоятельного решения, один похожий, другой – труднее.
Пример 6
Найти неопределенный интеграл.
![]()
Пример 7
Найти неопределенный интеграл.
![]()
Интегрирование неправильной дробно-рациональной функции
Перейдем к рассмотрению случая, когда старшая степень числителя больше либо равна старшей степени знаменателя.
Пример 8
Найти неопределенный интеграл.
![]()
Совершенно очевидно, что данная дробь является неправильной: ![]()
Основной метод решения интеграла с неправильной дробно-рациональной функций – это деление числителя на знаменатель. Алгоритм деления многочленов столбиком рассматривался на уроке Сложные пределы, и сейчас мы закрепим навыки.
Сначала рисуем «заготовку» для деления:
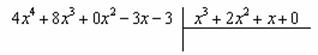
ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами
Теперь маленькая задачка, на какой множитель нужно умножить ![]() , чтобы получить
, чтобы получить ![]() ? Очевидно, что на
? Очевидно, что на ![]() :
:
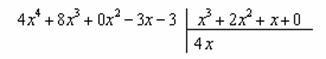
Далее умножаем ![]() сначала на
сначала на ![]() , потом – на
, потом – на ![]() , потом – на
, потом – на ![]() , потом – на 0 и записываем результаты слева:
, потом – на 0 и записываем результаты слева:
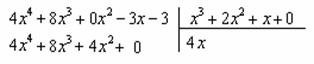
Проводим черточку и производим вычитание (из верха вычитаем низ):
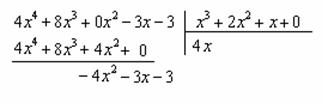
Старшая степень остатка ![]() равна двум, старшая степень делителя
равна двум, старшая степень делителя ![]() – больше, она равна трём, значит, больше разделить не удастся. Если бы изначально у нас был в числителе многочлен пятой степени, то алгоритм деления увеличился бы на один шаг.
– больше, она равна трём, значит, больше разделить не удастся. Если бы изначально у нас был в числителе многочлен пятой степени, то алгоритм деления увеличился бы на один шаг.
Итак, наше решение принимает следующий вид:
![]()
Делим числитель на знаменатель:
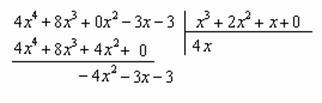
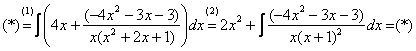
(1) Что дало деление? Много хорошего: теперь у нас два слагаемых, первое – интегрируется совсем просто, а второе – правильная дробь, которую мы решать уже умеем.
После деления всегда желательно выполнять проверку.
В рассматриваемом примере можно привести к общему знаменателю ![]() , и в результате получится в точности исходная неправильная дробь
, и в результате получится в точности исходная неправильная дробь ![]()
(2) От первого слагаемого сразу берем интеграл. Знаменатель дроби раскладываем на множители
Дальше всё идет по накатанной схеме:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
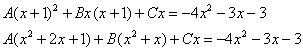
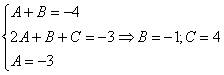
![]()
Готово.
И, наконец, заключительный пример для самостоятельного решения. Он очень интересен, рекомендую всем!
Пример 9
Найти неопределенный интеграл.
![]()
Только что обратил внимание, что во всех примерах урока в ходе решения систем у нас получались «хорошие» целые коэффициенты ![]() . По той причине, что почти все интегралы я взял из сборника Рябушко. На практике же
. По той причине, что почти все интегралы я взял из сборника Рябушко. На практике же, когда автор методички придумает какой-нибудь корявый интеграл, часто будут появляться разные нехорошести.
Таким образом, если в ходе решения интеграла от дробно-рациональной функции у Вас получаются дробные значения коэффициентов ![]() , то в этом нет ничего страшного, ситуация даже обыденна.
, то в этом нет ничего страшного, ситуация даже обыденна.
Желаю успехов!
Решения и ответы:
Пример 2. Решение:
![]()
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
![]()
![]()
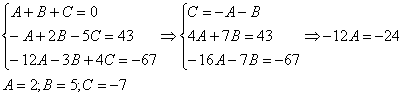
Комментарий: в правой части у нас нет слагаемого с ![]() , поэтому в первом уравнении системы ставим справа ноль.
, поэтому в первом уравнении системы ставим справа ноль.
![]()
Пример 4. Решение:
![]()
Шаг 1. Проверяем, правильная ли у нас дробь
Старшая степень числителя: 6
Старшая степень знаменателя: 8
![]() , значит, дробь является правильной.
, значит, дробь является правильной.
Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители. Множитель ![]() разложить нельзя, а вот
разложить нельзя, а вот ![]() – можно:
– можно:
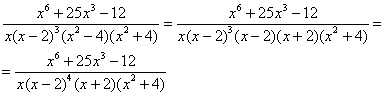
Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей.
В данном случае, разложение имеет следующий вид:
![]()
Пример 6. Решение:
![]()
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
![]()
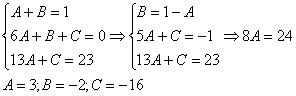

Пример 7. Решение:
![]()
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
![]()
![]()
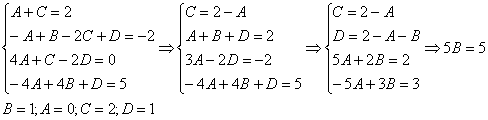
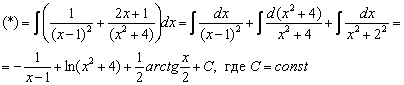
Пример 9. Решение:
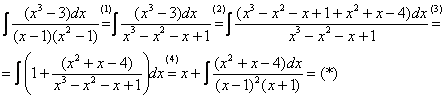
(1) Здесь неправильная дробь, поскольку старшие степени числителя и знаменателя равны: 3 = 3. Для того чтобы разделить числитель на знаменатель придётся временно раскрыть скобки в знаменателе.
(2)-(3) Теперь можно разделить ![]() на знаменатель
на знаменатель ![]() , но делать этого… я не буду. Можно поступить хитрее. Используем прием, который рассмотрен в первом параграфе урока Интегрирование некоторых дробей.
, но делать этого… я не буду. Можно поступить хитрее. Используем прием, который рассмотрен в первом параграфе урока Интегрирование некоторых дробей.
(4) От первого слагаемого сразу берем интеграл. Знаменатель оставшейся, уже правильной, дроби снова записываем в виде произведения множителей. Тут я немного подсократил разложение, надеюсь, всем понятно, что ![]()
Далее накатанная колея…
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
![]()
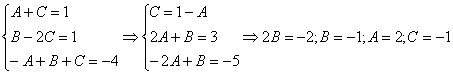
![]()
Вы выполнили проверку? – мож где ошибочка вышла ;)
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright