Производная по направлению и градиент функции

Уже в начале первой статьи о дифференцировании функции двух переменных я коротко рассказал о смысле частных производных 1-го порядка и подвёл вас к теме сегодняшнего урока. Итак, что же такое производная по направлению? На самом деле с данным понятием вы знакомы ещё с 1-го семестра, поскольку производную функции одной переменной смело можно назвать производной по направлению – ведь она характеризует скорость изменения функции в направлении оси .

И эта суть с учётом бОльшего разнообразия направлений распространяется на производные функций нескольких переменных, в частности, на производные функции . Геометрически функция двух переменных чаще всего представляет собой поверхность, и значения «зет» у нас чётко ассоциируются с высотой. Таким образом, с позиций геометрии скорость изменения данной функции – есть скорость изменения высоты. При этом совершенно понятно, что «негоризонтальная» поверхность изменчива – в каких-то направлениях она крутА, в каких-то полога, а где-то таки «равнина». И производная по направлению как раз призвана охарактеризовать «ландшафт местности» (скорость изменения функции) в различных точках по различным направлениям. В этой связи возникает первый вопрос:

а КАКИМ СПОСОБОМ вообще можно задать какое-то конкретное направление?

Вспомним забавную модель урока Предел функции двух переменных, в которой мы перемещаемся по комнате в плоскости декартовой системы , а прямо над нами «зависло одеяло», заданное функцией . Давайте встанем в некоторую точку области определения. В зависимости от выбора точки нам доступен бесконечно малый «шажок» в некоторых или, что вероятнее, во всех направлениях. Направление традиционно обозначается исходящим из точки лучом , лежащим в плоскости . Сам луч можно определить с помощью угла (между ним и осью либо ), а ещё лучше – с помощью вектора.

Вопрос второй:

как узнать скорость изменения функции 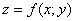в каком-либо направлении?

С помощью производной по направлению . Как вариант, в обозначении можно использовать букву «эф»: .

Если в точке существует производная по направлению луча (исходящего из точки и лежащего в плоскости ), то её можно рассчитать по следующей формуле:

, где:

– частные производные 1-го порядка в точке ;
– направляющие косинусы (координаты вектора единичной длины), однозначно определяющие данное направление.

Примечание: Производная по направлению, конечно же, не обязана существовать во всех возможных направлениях (представьте, например, «край одеяла»). Со строгими условиями её существования можно ознакомиться в учебной литературе.

На практике популярна более компактная запись: .

– это ЧИСЛО, характеризующее скорость изменения функции, причём:

– если , то функция в точке по данному направлению возрастает (поверхность «идёт в гору»);

– если , то функция в точке по данному направлению убывает («склон» поверхности);

– если , то функция в точке по данному направлению постоянна (поверхность параллельна плоскости ).

Геометрический смысл производной по направлению по существу напоминает геометрический смысл «обычной» производной. Представьте плоскость, проходящую через луч «эль» перпендикулярно плоскости . Данная плоскость «высекает» из поверхности пространственную линию , которой, очевидно, принадлежит точка . Производная по направлению численно равна тангенсу угла между касательной к линии в точке и плоскостью :

Примечание: также можно сказать, что – это угол между касательной к линии в точке и её ортогональной проекцией на плоскость , т.е. направлением луча (см. Пример 3, пункт «д» статьи Основные задачи на прямую и плоскость).

Более того, само обозначение символизирует отношение приращения функции («высоты») к бесконечно малому «шажку» по направлению луча «эль». Таким образом, чем больше по модулю, тем больше крутизна поверхности в данной точке по данному направлению. Крутизну можно выразить непосредственно через угол:

, после чего данная характеристика приобретает простой обывательский смысл («подъём в гору под углом 30 градусов» и т.п.). Впрочем, в геодезии приняты другие стандарты.

Как видите, всё очень и очень напоминает производную функции одной переменной – с тем отличием, что направлений стало гораздо больше, и по одну руку может быть «скала», а по другую – «пропасть». Кстати, все ли понимают, почему мы делаем именно бесконечно малые «шаги» по различным направлениям? Дело в том, что существует поверхности, «рельеф» некоторых меняется невероятно быстро – на 1 квадратном сантиметре могут запросто умещаться миллионы «гор» и «ущелий», да и того больше. Поэтому для корректного описания «местности» и используются бесконечно малые величины

После небольшого экскурса в теорию вернёмся к самой формуле , из которой выведем скорость изменения функции в двух хорошо знакомых направлениях.

Рассмотрим исходящий из точки луч , параллельный оси (либо совпавший с ней) и направленный в сторону её острия. Очевидно, что данный луч однозначно определяется единичным вектором . Таким образом, (напоминаю, что координаты вектора единичной длины – это и есть соответствующие направляющие косинусы) и общая формула чудесным образом упрощается:

То есть, частная производная «по икс» в точке характеризует скорость изменения функции в направлении острия оси (параллельно данной оси).

Самостоятельно проведите рассуждения для луча и сделайте вывод о том, что .

Теоретическая часть урока начинает плавно перетекать в практику, и первые задачи будут посвящены «трёхмерным аналогам» примеров статьи о смысле производной:

Пример 1

Найти производную функции в точке по направлению вектора

А теперь давайте немного разомнёмся и немного походим по комнате. Предположим, что под нами плоскость . Да-да, всё верно – сейчас мы перемещаемся ПО САМОЙ поверхности. На уроке Предел функции двух переменных нам помогал один волшебный персонаж, но сегодня настал черёд самостоятельно исследовать поверхности – чтобы как следует прочувствовать тему =)

Что с высотой? Очевидно, что в каком бы направлении мы ни пошли – высота будет оставаться неизменной. Таким образом, сразу понятно, что в любой точке и по любому направлению скорость изменения функции равна нулю.

Однако, несмотря на известный ответ и всю простоту задачи, со всей ответственностью отнесёмся к её решению:

Вычислим скорость изменения функции по направлению исходящего из точки луча , который определяется вектором . Используем рабочую формулу:

Найдём частные производные 1-го порядка:

В результате получены две константы, а именно, два нуля. Что это значит? Это значит, что частные производные равны нулю В ЛЮБОЙ точке области определения функции (вся плоскость ), в частности и в точке :

Примечание: формально частные производные можно расписать в виде и выполнить подстановку координат точки :

Полученные результаты подтверждают тот факт, что откуда бы и по какому бы направлению мы ни передвигались – наша высота будет сохраняться постоянной:

В принципе, здесь следует записать ответ, но ради отработки общего алгоритма решения найдём направляющие косинусы предложенного направления. По существу, требуется найти вектор единичной длины, который сонаправлен с вектором . Задача нахождения такого вектора подробно рассмотрена в самом конце статьи Скалярное произведение векторов. Воспользуемся готовой формулой:

Легко проверить, что любой другой ненулевой сонаправленный вектор приводится к этому же «эталону». Протестируем, например, вектор :

К слову, не лишним будет убедиться, что его длина действительно равна единице:

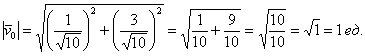
Эквивалентный способ проверки основан на известном равенстве :

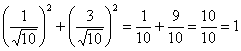
Собственно, финальный расчёт:

Ответ:

Можно использовать обозначение либо , подчёркивая, что производная по направлению найдена именно в точке . Однако упущение невелико, поскольку это и так ясно из контекста решения.

Легко понять, что проведённые выкладки справедливы и для любой другой «горизонтальной» плоскости, то есть производная функции в любой точке и по любому направлению равна нулю. Ну а сейчас самое время покинуть душные квартиры и выйти склон зелёного холма, где безмятежно пригревает майское солнышко. …Хотя кто знает, возможно, вы там и находитесь – ведь с развитием гаджетов люди стали получать знания в самых неожиданных местах =)

Но, так или иначе – добро пожаловать на природу:

Пример 2

Найти производную функции в точке по направлению:

1) координатных осей (параллельно им);
2) вектора ;
3) вектора ;
4) градиента.

Решение: итак, выберите произвольную точку «зелёного холма» и осмотритесь по сторонам. Теперь переместитесь в какую-нибудь другую точку плоскости и снова оцените «местность»:
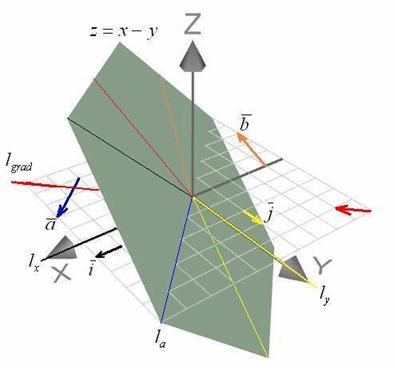
Производная по направлению характеризует крутизну поверхности в данном направлении

…кой-какие обозначения я не проставил из эстетических соображений, ну да ладно, не извращаться же со слоями в Фотошопе…

Что можно сказать о «ландшафте»? Во всех своих точках плоскость имеет постоянный наклон по всем направлениям, то есть, с точки зрения наклона – без разницы, где мы находимся. Проверим это аналитически:

Как и в предыдущем примере, производные-константы подразумевают тот факт, что в ЛЮБОЙ точке плоскости XOY, а значит и в точке (которую я выбрал исключительно для удобства построения чертежа), эти значения сохраняются постоянными:

Таким образом:
– и данный результат как раз убедительно подтверждает то, что скорость изменения функции зависит только от направления.

1) Найдём производную по направлению луча , совпадающего с положительной полуосью . Тут даже с направляющими косинусами возиться не надо – как было установлено выше, производная по данному направлению равна частной производной по «икс» в точке :

Для лучшего понимания я изобразил «чёрную дорожку», по которой мы будем «подниматься вверх по склону» и, исходя из геометрического смысла производной, очень легко отыскать конкретное значение «чёрного» угла: .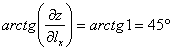

И ещё раз подчёркиваю независимость выбора исходной точки – если мы выберем любую другую «начальную точку путешествия» и начнём двигаться в направлении вектора , то «угол подъёма» будет точно таким же.

Аналогичная история с положительным направлением оси :

Отрицательный знак производной говорит об убывании функции в направлении координатного вектора . Иными словами, тут нас ожидает «желтая дорожка» вниз по склону под «жёлтым» углом градусов.

2) Вычислим производную по направлению луча . Для этого отработанным приёмом найдём единичный вектор , сонаправленный с вектором :
– координаты которого и являются направляющими косинусами данного направления:

Да, не забываем о проверке:
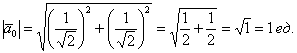, ч.т.п.

По правилам хорошего тона запишем вычисления подробно:

И действительно, синяя «дорожка» проходит на неизменной высоте прямо в плоскости .

Аналогично – если мы «выйдем» из любой другой точки плоскости по направлению того же вектора , то наша высота (скорость изменения функции) будет оставаться постоянной.

3) Найдём производную по направлению вектора :

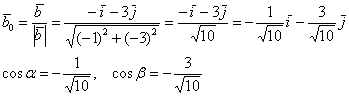
Проверим результат с помощью равенства :

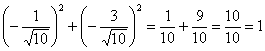
Вычислим производную по направлению луча , который «спрятался» под плоскостью :

Таким образом, подъём по «оранжевой дороге» осуществляется под углом

4) Градиент

Понятие градиента можно сформулировать по-разному. Начнём с локального определения, а именно, с градиента функции в отдельно взятой точке:

Градиентом функции в точке называется направленный отрезок , отложенный от точки , который показывает направление и скорость наискорейшего роста функции в данной точке.

Если совсем просто, то куда «смотрит» градиент – там и самый крутой «подъём в гору»

Распространённые обозначения: либо , причём здесь уже нельзя записывать просто (точнее, эта запись приобретает несколько другой смысл).

В нашем случае: .

И теперь заостряю внимание: градиент в точке – это вектор несвободный. По той причине, что характеризует поведение функции именно в данной точке, а не где-то ещё. Поэтому, следует отложить от начала координат. Однако он тоже оказывается под плоскостью , и «красный» вектор на чертеже, которым я обозначил общее направление – это на самом деле градиент в другой точке:

Взаимосвязь производной по направлению с градиентом:

Производная по некоторому направлению в точке – это проекция градиента в данной точке на данное направление:
, откуда, согласно известным геометрическим выкладкам (см. ссылку выше), получается весьма полезная практическая формула:

, где:

– длина градиента;
– угол между градиентом и данным направлением.

В свою очередь из этой формулы следует, что производная по направлению достигает максимального значения при , то есть когда – направление совпадает с направлением градиента.

В нашей задаче производная по направлению градиента:
и максимальный «красный» угол подъёма:

Заметьте, что полученный результат – это отличное средство дополнительного контроля решения: если по другому направлению получился бОльший угол, то нужно искать ошибку.

Как всегда, в лучших своих традициях я аккуратно встроил теоретический материал в развёрнутое практическое задание, и после увлекательной прогулки настало время подвести итог:

Ответ:

Если что-то осталось недопонятым, то, вероятнее всего, у вас пробелы в теории производной функции одной переменной и/или основах аналитической геометрии. Особенно много сегодня требуется геометрических знаний. Спокойствие и только спокойствие – всё можно наверстать буквально в ближайший час, после чего вернуться на эту страницу и перечитать начало статьи ещё раз.

Ну а мы продолжаем рассматривать тематические задачи, и оставшиеся примеры будут значительно короче. Но расслабляться ни в коем случае не следует, поскольку впереди ещё немало нового и интересного материала:

Пример 3

Дана функция , точка и вектор . Требуется найти:
а) производную функции в точке по направлению вектора ;
б) градиент функции в данной точке.

Классика жанра – найти производную по какому-нибудь направлению и градиент.

Закрепляем алгоритм решения:

а) Обозначим через исходящий из точки по направлению вектора луч и воспользуемся стандартной формулой:

Найдём частные производные 1-го порядка:

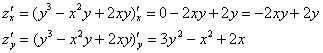
Тут не помешает «прозвонить» равенство , благо, смешанные производные 2-го порядка отыскиваются с пол тычка.

А вот сейчас наступает действительно ответственный момент – это «реальное» вычисление частных производных 1-го порядка в точке . Всегда проявляйте ПОВЫШЕНОЕ ВНИМАНИЕ на данном этапе:

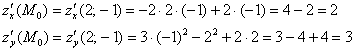
Полезный приём: несмотря на кажущееся отсутствие хорошей проверки, я всё-таки придумал небольшое ноу-хау, которое с высокой эффективностью позволяет избегать вычислительных ошибок. Ухищрение состоит в следующем: когда вам предложена задача с неприятными и плохо проверяемыми вычислениями, то сначала СОСРЕДОТОЧЕННО прорешайте её на черновике и отложите листок в сторону. Далее переключаемся на другие дела, после чего черновое решение благополучно забывается. Спустя некоторое время (полчаса - час, а ещё лучше – день) так же ВНИМАТЕЛЬНО оформляем чистовое решение и сверяемся с черновиком. Почти 100% – ошибка «не пройдёт».

На очереди нахождение единичного вектора, сонаправленного с вектором :

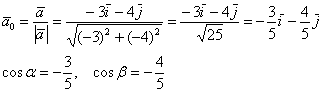
Контроль: , в чём и требовалось убедиться.

На завершающем этапе тоже проявляем внимание, правда, здесь уже гораздо меньше шансов что-то «прозевать»:

И конечно, не забываем о геометрическом смысле результата: отрицательный знак производной сообщает нам об убывании функции в данном направлении, т.е. при бесконечно малом «шажке» из точки по направлению луча «эль» крутизна «склона» поверхности составит .

Особо подчёркиваю, что в отличие от Примеров № 1, 2 оговорка о «бесконечно малом шажке» становится необходима, ибо многие поверхности – это «не плоскости плоские», а «волны волнистые», и в соседней, пусть даже очень близкой точке производная по тому же направлению в общем случае будет другой.

Кстати, в условии запросто может спрашиваться НЕ о производной по направлению, а о крутизне поверхности – и в этом случае расчёт угла станет обязательным завершающим шагом решения.

2) Второй пункт совсем прост:

Однако и тут снова следует проявить аккуратность – условие задачи вполне может запрашивать НЕ градиент, а «наибольшую скорость роста функции в точке ». Тогда находим производную по направлению градиента:
, которая и является мерилом этой скорости.

А если же требуется найти «наибольшую крутизну поверхности в точке », то в ответе указываем НЕ градиент и НЕ его длину, а угол .

Завершая этот содержательный разбор полётов, расскажу о более широком понятии градиента. В более широком смысле под градиентом понимают векторную функцию , которая каждой точке области определения функции (где существует градиент) ставит в соответствие вектор, показывающий направление максимального роста функции в данной точке.

Так, например, в нашем случае можно составить векторную функцию и для десятка-другого точек построить целую «карту» направленных отрезков, которая безо всякого трёхмерного чертежа достаточно хорошо охарактеризует «поведение» поверхности в интересующих нас направлениях.

Отсюда становится окончательно понятно, почему градиент в точке – это несвободный вектор, отложенный именно от конкретной точки.

Молодцы, что осилили =) ...теперь и теория поля будет нипочём!

Ответ:

Пара типовиков для самостоятельного решения:

Пример 4

Найти производную функции в точке по направлению вектора и максимальную крутизну поверхности в данной точке.

Слишком просто? В простых задачах и ошибаются! …ну что же, сами виноваты – задачка позанятнее:)))

Пример 5

Найти производную функции в точке в направлении, составляющем угол с градиентом функции в этой точке.

Если возникли затруднения, пожалуйста, вернитесь к вышеизложенному материалу. Примерный образец чистового оформления решений в конце урока.

На практике довольно часто встречаются задания, в которых направление задаётся другими способами:

Пример 6

Найти производную функции в точке :
а) в направлении, составляющем угол с положительным направлением оси ;
б) в направлении биссектрисы 2-го координатного угла.

То есть, направления заданы через углы. Учимся с ними разбираться:

Решение: частные производные в точке понадобятся в обоих пунктах и поэтому в первую очередь их и найдём:

Ну а что тут такого? Числа как числа.

а) Обозначим через луч, исходящий из точки и образующий угол с положительным направлением оси . Очевидно, что данный луч лежит в 1-й координатной четверти (правой верхней) и образует угол в с осью . Картина очень простая, но если таки мутноватая, выполните чертёж.

Формула производной по направлению, естественно, та же:

И главный вопрос – как найти направляющие косинусы? Я предлагаю следующую цепочку рассуждений, которая мне показалась наиболее простой:

Пусть направляющий вектор луча отложен от начала координат. Совершенно понятно, что этот вектор тоже наклонен к оси под углом 30 градусов.

Угол – это угол между вектором и положительной полуосью . То есть, угол сразу «готов к употреблению» – даже обозначения совпали (в условии вполне могла быть и другая буква, например, ).

Угол – это угол между вектором и положительной полуосью . С «бетой» никаких проблем: поскольку угол между координатными осями составляет 90 градусов, то или .

Вычислим направляющие косинусы:

Впрочем, чего тут вычислять – эти значения вкладывались в наши головы долгие школьные годы. Но на всякий случай ссылка на тригонометрическую таблицу.

Контроль: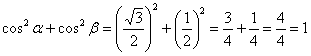
Дотошные естествоиспытатели могут изобразить на чертеже вектор 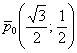и воочию убедиться, что он направлен туда, куда надо.

Искомая производная по направлению:

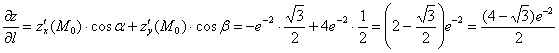
…это ещё божий одуванчик, бывает гораздо хуже.

б) Вычислим производную в направлении биссектрисы 2-го координатного угла. Напоминаю, что координатные четверти нумеруются против часовой стрелки, и очевидно, речь идёт о биссектрисе, которая делит пополам левую верхнюю четверть.

Мало-мальски подготовленные люди легко подберут направляющий вектор этого направления, напрашивается вектор , и сразу найдут направляющие косинусы:

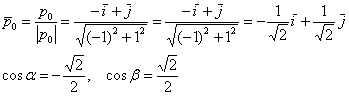
Такой вариант решения вполне приемлем, однако «подарочный» угол, кратный 45 градусам, встречается далеко не каждый день, и поэтому мы отработаем универсальную схему решения. Пусть вектор , задающий биссектрису 2-го координатного угла, отложен от начала координат (как вы уже поняли, именно в таком положении проще всего высмотреть нужные углы):
(угол между вектором и положительной (!) полуосью );
(угол между вектором и положительной полуосью ).
Таким образом:

Обозначим буквой луч, который исходит из точки в направлении биссектрисы 2-го координатного угла. Вычислим производную по данному направлению:

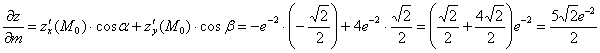
Ответ:

На практике так подробно, конечно, расписывать не нужно и решение следующей задачи поможет вам понять ориентировочный минимум комментариев:

Пример 7

Найти производную функции в точке :
а) в направлении, составляющем угол с положительным направлением оси ;
б) в направлении биссектрисы 4-го координатного угла.

И в заключение этого параграфа хочу отметить, что помимо геометрии, рассматриваемый математический инструментарий широко применяется в различных физических задачах – примеров настолько много, что от физики могут взвыть даже некоторые физики =)
В этой связи я сохраню мудрое молчание, …впрочем, ненадолго =)

Производная по направлению и градиент функции трёх переменных

Грубо говоря, добавляется одно измерение и одно слагаемое. Рассмотрим функцию трёх переменных и точку , принадлежащую её области определения.

Если в точке существует производная по направлению пространственного луча (исходящего из точки ), то её можно рассчитать по следующей формуле:

, где:

– частные производные функции трёх переменных в точке ;
– направляющие косинусы данного направления (они же соответствующие координаты направляющего вектора единичной длины).

Градиентом функции в точке называется направленный отрезок , отложенный от точки , который указывает направление наибыстрейшего возрастания данной функции в данной точке.

И обещанный физический пример: рассмотрим функцию трёх переменных , которая характеризует температуру некоего пространственного тела в каждой его точке . Тогда производная по тому или иному направлению в некоторой точке тела будет показывать скорость нагревания/охлаждения тела в соответствующих направлениях, а вектор – указывать направление наибыстрейшего роста температуры в этой точке.

Вот такой вот удачный и понятный пример – не какие-нибудь плохо представляемые электрические поля.

Закрепим формулы несколькими задачами:

Пример 8

Найти производную функции в точке по направлению вектора

Не тушуемся, это пространственный вектор:

Алгоритм решения остаётся прежним. Вычислим частные производные 1-го порядка в точке . Вот уж где точно нужен глаз да глаз:

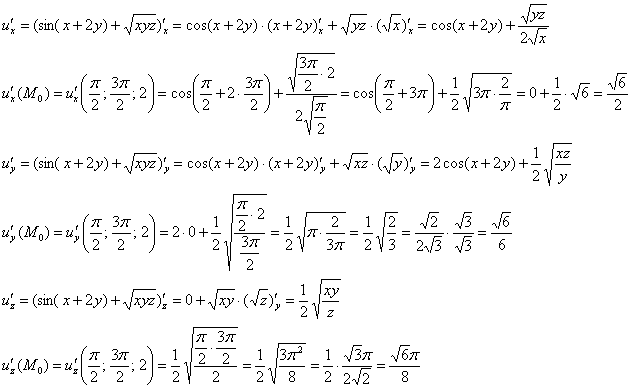
Найдем направляющие косинусы данного направления:

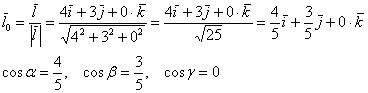
Контроль:

И завершающий шаг:

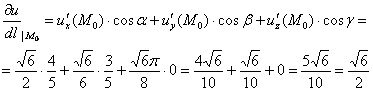
Ответ:

Пара символических заданий для самостоятельного решения:

Пример 9

Найти производную функции в точке по направлению, составляющему с положительными координатными полуосями равные углы.

Пример 10

Найти направление и величину наибыстрейшего возрастания функции в точке .

Особых комментариев я не оставлял, поскольку всё очень похоже на примеры 1-й части урока.

Аналогичным образом производная по направлению и градиент определяются и для функций бОльшего количества переменных.

Всех поздравляю! – сегодня мы не только познакомились с новым материалом, но и обобщили понятие производной, после чего ~~забудем о ней, как о кошмарном сне~~ можно смело приступать к изучению интегралов, разновидностей коих – великое множество...
…чувствую-чувствую, что взгрустнулось – вот и решил приободрить =)

Желаю вам выбора удачных направлений, которые, кстати, далеко не во всех точках жизни направлены по градиенту.

Спасибо за внимание и до скорых встреч!

Решения и ответы:

Пример 4: Решение: вычислим частные производные 1-го порядка в точке :

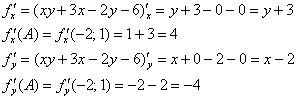
Найдём направляющие косинусы:

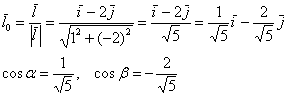
Искомая производная по направлению:

Найдём градиент функции в точке и вычислим его длину:

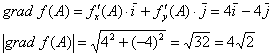
Таким образом, максимальная крутизна поверхности в точке :

Ответ:

Пример 5: Решение: вычислим частные производные 1-го порядка в точке :

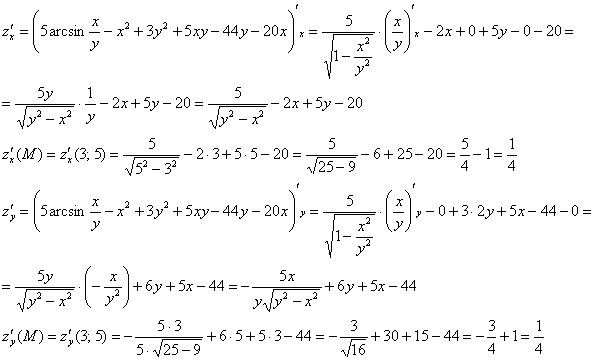
Составим градиент функции в точке и вычислим его длину:

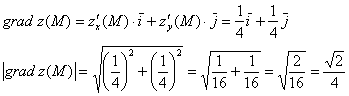
Искомая производная по направлению:

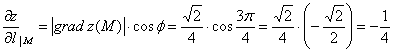
Ответ:

Пример 7: Решение: вычислим частные производные 1-го порядка в точке :

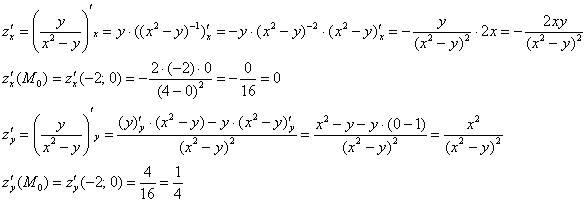
а) Вычислим производную по направлению , составляющему угол с положительным направлением оси . Рассмотрим единичный вектор , определяющий это направление. Очевидно, что . Таким образом:

Искомая производная по направлению:

б) Рассмотрим единичный вектор , определяющий направление биссектрисы 4-го координатного угла. Очевидно, что его углы с положительными полуосями и соответственно равны (можно взять – ориентация угла не имеет значения) и . Таким образом:

В результате производная по данному направлению:

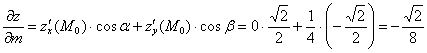
Ответ:

Пример 9: Решение: вычислим частные производные 1-го порядка в точке :

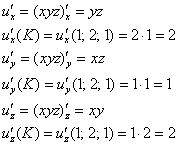
Найдём направляющие косинусы предложенного направления. Используем равенство:

Так как , то:

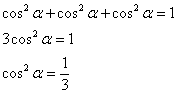
И поскольку луч расположен в 1-м октанте:

Искомая производная по направлению:

Ответ:

Пример 10: Решение: вычислим частные производные 1-го порядка в точке :

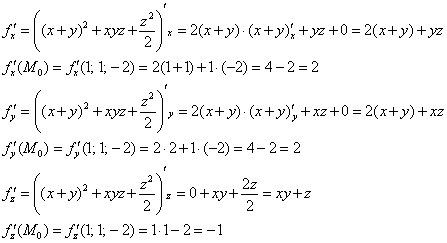
Направление наибыстрейшего роста функции в точке задаёт вектор градиента в данной точке:

Вычислим величину наибыстрейшего роста функции:

Ответ:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?