


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
12. Проверка статистических гипотез
Продолжаем проверять статистические гипотезы – всё новые и новые, новые и новые, до полного насыщения! Исправляя оплошность (запамятовал), хочу порекомендовать эту увлекательную тему в качестве основного или дополнительного материала для вашего научного проекта (курсовика, диплома, диссертации) или прикладного исследования. Причём, самому широкому кругу читателей, в том числе экономистам, социологам, психологам – всем, кто работает со статистическими данными. Здесь и научная новизна, и практическая значимость, и широкий простор для творчества! И несложные вычисления, что немаловажно. ! И сразу дисклеймер предупреждение: в рамках сайта я рассматриваю лишь учебные задачи, поэтому при выборе статических методов для серьёзного научного труда лучше обратиться к другим источникам.
Как вы знаете (а если нет, то ссылка выше), все статистические гипотезы делятся на два вида:
I) Гипотеза о законе распределения статистической совокупности. Этому виду гипотез посвящен следующий урок – Критерий согласия Пирсона.
II) Вторая большая группа гипотез касается числовых характеристик стат. совокупностей, закон распределения которых уже известен:
– Гипотеза о генеральной средней нормального распределения – именно с неё мы и начали разминку;
– Гипотеза о равенстве генеральных средних двух распределений – 4 случая, все разберём!
– Гипотеза о генеральной дисперсии нормального распределения;
– Гипотеза о равенстве ген. дисперсий двух нормальных распределений;
– Гипотеза о вероятности события;
– Сравнение вероятностей двух биномиальных распределений.
Существуют и другие статистические гипотезы, с которыми можно ознакомиться, например, в учебном пособии В. Е. Гмурмана (поздние издания). Кроме того, в курсе корреляционно-регрессионного анализа я рассмотрю статистические гипотезы о значимости линейного коэффициента корреляции, коэффициентов уравнения регрессии и самого уравнения (коэффициента детерминации).
Вникаем, решаем и получаем удовольствие!
Гипотеза о равенстве генеральных средних двух распределений
Постановка задачи: из двух генеральных совокупностей извлечены выборки объёмов ![]() и
и ![]() и найдены их выборочные средние:
и найдены их выборочные средние: ![]() и
и ![]() соответственно. Требуется на уровне значимости
соответственно. Требуется на уровне значимости ![]() проверить гипотезу
проверить гипотезу ![]() о равенстве генеральных средних против одной из следующих конкурирующих гипотез:
о равенстве генеральных средних против одной из следующих конкурирующих гипотез: ![]() ,
, ![]() или
или ![]() . Как и в гипотезе о значении генеральной средней, в первом случае строится левосторонняя критическая область, во втором – правосторонняя и в третьем – двусторонняя.
. Как и в гипотезе о значении генеральной средней, в первом случае строится левосторонняя критическая область, во втором – правосторонняя и в третьем – двусторонняя.
При этом возможны следующие вариации задачи:
а) выборки независимы, генеральные совокупности распределены нормально и известны их дисперсии 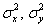 .
.
Тогда для проверки нулевой гипотезы используют статистический критерий 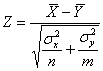 , где
, где ![]() – случайные значения выборочных средних
– случайные значения выборочных средних
Критическая область однозначно определяется критическим значением ![]() , которое отыскивается из соотношения
, которое отыскивается из соотношения ![]() для односторонней области и
для односторонней области и ![]() – для двусторонней, где
– для двусторонней, где ![]() – выбранный уровень значимости, а
– выбранный уровень значимости, а ![]() – функция Лапласа. Не поленюсь и снова нарисую все три случая, критическая область изображена красным цветом:
– функция Лапласа. Не поленюсь и снова нарисую все три случая, критическая область изображена красным цветом:
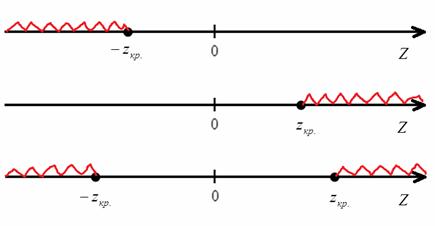
Далее на основании выборочных данных рассчитывается наблюдаемое значение критерия:
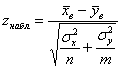
Если ![]() в критическую область НЕ попадает, то гипотезу
в критическую область НЕ попадает, то гипотезу ![]() на уровне значимости
на уровне значимости ![]() принимаем. Если же попадает, то нулевая гипотеза отвергается в пользу альтернативной гипотезы
принимаем. Если же попадает, то нулевая гипотеза отвергается в пользу альтернативной гипотезы ![]() .
.
Пример 40
По выборке объема ![]() найден средний вес изделий
найден средний вес изделий ![]() г изделий, изготовленных на первом станке; по выборке объема
г изделий, изготовленных на первом станке; по выборке объема ![]() найден средний вес изделий
найден средний вес изделий ![]() г изделий, изготовленных на втором станке. Известны генеральные дисперсии
г изделий, изготовленных на втором станке. Известны генеральные дисперсии ![]() . Требуется на уровне значимости 0,01 проверить нулевую гипотезу
. Требуется на уровне значимости 0,01 проверить нулевую гипотезу ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() . Предполагается, что генеральные совокупности распределены нормально, а выборки независимы.
. Предполагается, что генеральные совокупности распределены нормально, а выборки независимы.
...я, конечно, не знаю, у каких современных станков могут быть такие конские дисперсии, тут, скорее, речь о двух бабулях, которые пекут одинаковые пирожки дедовским методом :) И нужно выяснить, одинаковый ли у них выхлоп или первая бабушка более щедрая.
Решаем: по условию, известны генеральные дисперсии, поэтому для проверки гипотезы о равенстве генеральных средних используем критерий 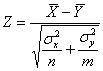 .
.
Для конкурирующей гипотезы ![]() строится правостороння критическая область. Критическое значение найдём из соотношения
строится правостороння критическая область. Критическое значение найдём из соотношения ![]() . По условию,
. По условию, ![]() :
:
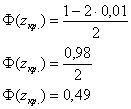
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем, что этому значению функции соответствует аргумент ![]() . Таким образом, при
. Таким образом, при ![]() нулевая гипотеза принимается, а при
нулевая гипотеза принимается, а при ![]() отвергается:
отвергается:

На чистовике эти чертежи выполнять не обязательно – они нужны, чтобы вы лучше видели ситуацию.
По выборочным данным вычислим наблюдаемое значение критерия:
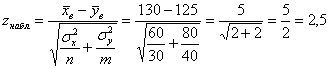
![]() , поэтому на уровне значимости 0,01 гипотезу
, поэтому на уровне значимости 0,01 гипотезу ![]() отвергаем. Иными словами, выборочные средние
отвергаем. Иными словами, выборочные средние ![]() статистически значимо отличаются друг от друга, и это отличие вряд ли объяснимо случайными факторами. А объяснимо оно именно различием генеральных средних.
статистически значимо отличаются друг от друга, и это отличие вряд ли объяснимо случайными факторами. А объяснимо оно именно различием генеральных средних.
Но это ещё не значит, что нужно покупать пирожки у «иксовой» бабули, они ведь могут оказаться менее вкусными :)
Ответ: на уровне значимости 0,01 нулевую гипотезу отвергаем.
И еще раз повторим, что это значит. Это значит, что с вероятностью 1% мы совершили ошибку первого рода (отвергли правильную гипотезу).
Следующая задача для самостоятельного решения:
Пример 41
Из продукции двух автоматических линий извлечены по 50 гвоздей и вычислены их выборочные средние длины ![]() и
и ![]() мм. Нормативная погрешность линий есть нормальная случайная величина с дисперсией
мм. Нормативная погрешность линий есть нормальная случайная величина с дисперсией ![]() . На уровне значимости 0,05 проверить гипотезу о равенстве генеральных средних
. На уровне значимости 0,05 проверить гипотезу о равенстве генеральных средних ![]() против конкурирующих гипотез: а)
против конкурирующих гипотез: а) ![]() , б)
, б) ![]() .
.
Краткое решение и ответ в конце урока, особую аккуратность проявите в обозначениях – в аналогичных задачах они бывают разными.
Та же гипотеза, другая ситуация:
б) независимые выборки достаточно большие 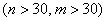 , генеральные дисперсии неизвестны, причём ген. совокупности могут иметь и другое распределение (не нормальное)
, генеральные дисперсии неизвестны, причём ген. совокупности могут иметь и другое распределение (не нормальное)
Условие ![]() , к слову, желательно и в предыдущем пункте.
, к слову, желательно и в предыдущем пункте.
В этом случае можно использовать похожий, но приближенный критерий 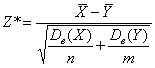 , где
, где ![]() – случайные значения выборочных средних, а
– случайные значения выборочных средних, а ![]() – соответствующие выборочные дисперсии.
– соответствующие выборочные дисперсии.
Исправлением дисперсий тут можно пренебречь (т.к. выборки большие), но лично я бы исправил. Впрочем, результаты такой проверки всё равно будут менее «авторитетными».
Ситуация более тяжелая:
в) это малые независимые выборки 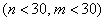 , ген. совокупности распределены нормально и дисперсии их не известны
, ген. совокупности распределены нормально и дисперсии их не известны
В этом случае выборочные дисперсии дают плохую оценку генеральных дисперсий, поэтому критерий предыдущего пункта не годится. Но если предположить или доказать, что генеральные дисперсии одинаковы (хотя и не известны), то для проверки гипотезы ![]() можно использовать следующий критерий:
можно использовать следующий критерий:
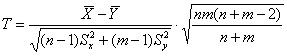 , где
, где ![]() – случайные значения выборочных средних, а
– случайные значения выборочных средних, а ![]() – соответствующие исправленные выборочные дисперсии. Эта случайная величина распределена по закону Стьюдента с
– соответствующие исправленные выборочные дисперсии. Эта случайная величина распределена по закону Стьюдента с ![]() степенями свободы.
степенями свободы.
Пример 42
Из двух партий деталей, изготовленных одинаковыми станками, извлечены выборки объемами ![]() и
и ![]() деталей. По результатам исследования найдены
деталей. По результатам исследования найдены ![]() мм,
мм, ![]() мм и
мм и ![]() мм,
мм, ![]() мм. Предполагая, что погрешность изготовления есть нормальная случайная величина, проверить на уровне значимости
мм. Предполагая, что погрешность изготовления есть нормальная случайная величина, проверить на уровне значимости ![]() гипотезу
гипотезу ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() .
.
В этом тяжелом случае нам удалось раздобыть всего лишь 10 и 15 гвоздей, но ситуацию спасает то, что станки одинаковые, поэтому можно смело допустить, что их погрешности (ген. дисперсии) одинаковы. Кроме того, можно проверить гипотезу о равенстве генеральных дисперсий, до которой мы ещё доберёмся.
Решение: полагая, что генеральные дисперсии одинаковы, используем критерий 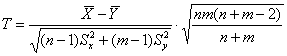 .
.
Поскольку конкурирующая гипотеза имеет вид ![]() , то критическая область двусторонняя. Найдём критическое значение. Для уровня значимости
, то критическая область двусторонняя. Найдём критическое значение. Для уровня значимости ![]() и числа степеней свободы
и числа степеней свободы ![]() по таблице или с помощью Калькулятора (Пункт 10в) определяем:
по таблице или с помощью Калькулятора (Пункт 10в) определяем:
![]()
При ![]() нулевая гипотеза принимается, а вне этого интервала – отвергается:
нулевая гипотеза принимается, а вне этого интервала – отвергается:
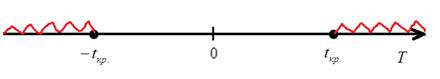
Вычислим наблюдаемое значение критерия:
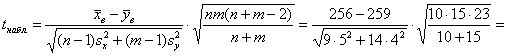
![]() – полученное значение попало в область принятия гипотезы.
– полученное значение попало в область принятия гипотезы.
Таким различие выборочных средних ![]() статистически не значимо и объяснимо влиянием случайных факторов (погрешностью станков и тем, что в саму выборку попали случайные гвозди).
статистически не значимо и объяснимо влиянием случайных факторов (погрешностью станков и тем, что в саму выборку попали случайные гвозди).
Ответ: на уровне значимости 0,05 гипотезу ![]() принимаем.
принимаем.
Задача для самостоятельного решения будет в параграфе Гипотеза о равенстве двух генеральных дисперсий, поскольку для того, чтобы пользоваться равенством ген. дисперсий, строго говоря и по меньшей мере, его нужно ещё проверить статистически.
И ещё один случай:
г) ген. совокупности распределены нормально, ген. дисперсии неизвестны, выборки зависимы
Здесь рассматриваются выборки одинакового объёма, варианты которых попарно зависимы. Что это значит? Пример: возьмём 50 помидоров и измерим их диаметр линейкой: ![]() . Затем в том же порядке – штангенциркулем:
. Затем в том же порядке – штангенциркулем: ![]() . Совершенно понятно, что соответствующие результаты будут хоть чуть-чуть, но различны:
. Совершенно понятно, что соответствующие результаты будут хоть чуть-чуть, но различны: ![]() , следовательно, выборочные средние – тоже:
, следовательно, выборочные средние – тоже: ![]() . И возникает вопрос: значимо или незначимо это отличие?
. И возникает вопрос: значимо или незначимо это отличие?
В случае зависимых выборок гипотеза о равенстве генеральных средних сводится к уже разобранной гипотезе о значении генеральной средней. Представим, что описанные выше попарные опыты проводятся много-много раз. Тогда речь заходит о случайной величине ![]() – случайной разнице между случайными значениями
– случайной разнице между случайными значениями ![]() выборочных средних. И мы проверяем гипотезу о том, что генеральная средняя (матожидание) этой разницы равна нулю
выборочных средних. И мы проверяем гипотезу о том, что генеральная средняя (матожидание) этой разницы равна нулю ![]() против очевидной альтернативы
против очевидной альтернативы ![]() или
или ![]() либо
либо ![]() .
.
Технику решения рассмотрим на конкретном примере, социологическая задача, и никаких гвоздей:
Пример 43
Физическая подготовка 9 спортсменов была проведена при поступлении в спортивную школу, а затем после недели тренировок. Итоги проверки в баллах оказались следующими:

(в 1-й строке число баллов при поступлении, во 2-й – после недели тренировок)
Требуется на уровне значимости 0,05 установить, значимо или незначимо улучшилась физическая подготовка спортсменов, в предположении, что число баллов распределено нормально.
И предположение это небезосновательно, т. к. человеческие характеристики, как правило, распределены нормально.
Решение: проверим гипотезу о том, что матожидание случайной величины ![]() (разницы между случайными средними) равно нулю
(разницы между случайными средними) равно нулю ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() (т.к. улучшение физической формы выражается бОльшим «игрековым» значением и отрицательной разностью).
(т.к. улучшение физической формы выражается бОльшим «игрековым» значением и отрицательной разностью).
Так как генеральная дисперсия этой случайной величины не известна, то используем знакомый критерий ![]() , где
, где ![]() – случайная разница между выборочными средними и
– случайная разница между выборочными средними и ![]() – соответствующее исправленное стандартное отклонение. Напоминаю, что этот критерий имеет распределение Стьюдента с количеством степеней свободы
– соответствующее исправленное стандартное отклонение. Напоминаю, что этот критерий имеет распределение Стьюдента с количеством степеней свободы ![]() .
.
Для уровня значимости ![]() и
и ![]() найдём критическое значение левосторонней критической области (по нижней строке таблицы или на Калькуляторе - Пункт 10в):
найдём критическое значение левосторонней критической области (по нижней строке таблицы или на Калькуляторе - Пункт 10в):
![]()
При ![]() нулевую гипотезу принимаем, а при
нулевую гипотезу принимаем, а при ![]() – отвергаем:
– отвергаем:
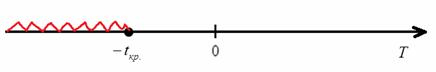
Для нахождения наблюдаемого значения критерия ![]() нужно рассчитать выборочные характеристики. Вычислим разности между вариантами
нужно рассчитать выборочные характеристики. Вычислим разности между вариантами ![]() , их квадраты
, их квадраты ![]() и суммы:
и суммы:
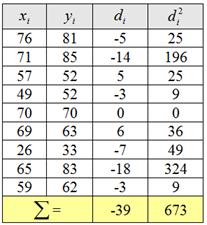
Вычислим выборочную среднюю разницу:
![]()
Вычислим исправленное стандартное отклонение, не сторонник я «ускоренных» формул, но здесь она удобна:

Таким образом:
![]() , поэтому на уровне значимости 0,05 нет оснований отвергать гипотезу
, поэтому на уровне значимости 0,05 нет оснований отвергать гипотезу ![]() .
.
В данном случае это более удачная формулировка, нежели «гипотезу принимаем».
Таким образом, средняя разница ![]() между вариантами
между вариантами ![]() (физ. форма до тренировки) и соответствующими вариантами
(физ. форма до тренировки) и соответствующими вариантами ![]() (физ. форма после тренировки) статистически незначима.
(физ. форма после тренировки) статистически незначима.
Ответ: на уровне значимости 0,05 нет оснований утверждать, что после недельной тренировки физическая форма спортсменов значимо улучшилась.
Продолжаем тему самостоятельно:
Пример 44
Две химические лаборатории исследовали 8 проб на допинг одним и тем же методом. Получены следующие результаты (процент содержания некоторого вещества в соответствующих пробах):

Требуется на уровне значимости 0,05 определить, значимо или незначимо различаются средние результаты анализов, в предположении, что они распределены нормально.
Иными словами, определите, не занесли ли в какую-нибудь лабораторию деньги :)
Как обычно, все числа уже в Экселе; продублирую также ссылки на таблицу критических точек распределению Стьюдента и Калькулятор (Пункт 10в).
С другими гипотезами всё проще:
Гипотеза о генеральной дисперсии нормального распределения
Она по своей сути похожа на гипотезу о генеральной средней: есть основания полагать, что генеральная дисперсия ![]() нормальной совокупности равна некоторому значению
нормальной совокупности равна некоторому значению ![]() . По результатам выборки объёма
. По результатам выборки объёма ![]() найдена исправленная выборочная дисперсия
найдена исправленная выборочная дисперсия ![]() и возникает вопрос: она значимо отличается от
и возникает вопрос: она значимо отличается от ![]() или нет? Таким образом, на уровне значимости
или нет? Таким образом, на уровне значимости ![]() требуется проверить гипотезу
требуется проверить гипотезу ![]() – о том, что генеральная дисперсия действительно равна своему гипотетическому значению.
– о том, что генеральная дисперсия действительно равна своему гипотетическому значению.
Для проверки этой гипотезы используют критерий ![]() , где
, где ![]() – случайное значение исправленной дисперсии. Данная случайная величина имеет распределение хи-квадрат с количеством степеней свободы
– случайное значение исправленной дисперсии. Данная случайная величина имеет распределение хи-квадрат с количеством степеней свободы ![]() и принимает лишь неотрицательные значения.
и принимает лишь неотрицательные значения.
Критическая область зависит от вида конкурирующей гипотезы, а критические значения можно определить по соответствующей таблице либо с помощью Калькулятора (Пункт 11б).
1) Для гипотезы ![]() строится левосторонняя область, критическое значение равно
строится левосторонняя область, критическое значение равно ![]() .
.

2) Для гипотезы ![]() строится правосторонняя область, критическое значение равно
строится правосторонняя область, критическое значение равно ![]() .
.

3) И для гипотезы ![]() строится двусторонняя критическая область, левая и правая критические точки определяются по формулам
строится двусторонняя критическая область, левая и правая критические точки определяются по формулам ![]() ,
, ![]()

Если наблюдаемое значение критерия ![]() попадает в критическую область, то гипотеза
попадает в критическую область, то гипотеза ![]() на уровне значимости
на уровне значимости ![]() отвергается.
отвергается.
Классическая задача по теме – это задача о точности какого-нибудь прибора, станка или метода измерения:
Пример 45
Допустимая погрешность измерительного прибора по паспорту составляет ![]() . В результате 10 измерений найдено фактическое значение погрешности
. В результате 10 измерений найдено фактическое значение погрешности ![]() . Требуется на уровне значимости 0,05 проверить, соответствуют ли экспериментальный результат заявленной точности прибора.
. Требуется на уровне значимости 0,05 проверить, соответствуют ли экспериментальный результат заявленной точности прибора.
Или, попросту говоря, не лажает ли этот прибор.
Решение: полагая, что погрешность измерений распределена нормально, проверим гипотезу о том, что генеральная дисперсия действительно равна ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() . Это, кстати, самый популярный вид альтернативной гипотезы – когда есть превышение нормы, и требуется проверить, случайно оно или нет.
. Это, кстати, самый популярный вид альтернативной гипотезы – когда есть превышение нормы, и требуется проверить, случайно оно или нет.
Используем критерий ![]() , где
, где ![]() – случайное значение исправленной дисперсии.
– случайное значение исправленной дисперсии.
Найдём правостороннюю критическую область. Для уровня значимости ![]() и количества степеней свободы
и количества степеней свободы ![]() по таблице критических точек распределения хи-квадрат или с помощью Калькулятора (Пункт 11б) определяем критическое значение:
по таблице критических точек распределения хи-квадрат или с помощью Калькулятора (Пункт 11б) определяем критическое значение:
![]()
При ![]() нулевая гипотеза принимается, а при
нулевая гипотеза принимается, а при ![]() – отвергается:
– отвергается:

Вычислим наблюдаемое значение критерия:
![]() , поэтому на уровне значимости 0,05 нет оснований отвергать гипотезу
, поэтому на уровне значимости 0,05 нет оснований отвергать гипотезу ![]() . Таким образом, выборочный более высокий результат
. Таким образом, выборочный более высокий результат ![]() с большой вероятностью обусловлен случайностью.
с большой вероятностью обусловлен случайностью.
Возможно, у вас сложилось впечатление, что значения 5 и 6,2 различаются существенно, но это иллюзия – ведь дисперсия имеет квадратичную размерность, и стандартные отклонения действительно довольно близкИ друг к другу: ![]() .
.
Ответ: на уровне значимости 0,05 точность прибора соответствует норме.
Самостоятельно:
Пример 46
Партия изделий принимается, если дисперсия контролируемого размера значимо не превышает 0,2. Исправленная выборочная дисперсия, найденная по выборке объема ![]() , оказалась равной
, оказалась равной ![]() . Можно ли принять партию на уровне значимости 0,05?
. Можно ли принять партию на уровне значимости 0,05?
Таблица здесь не годится, поэтому пользуемся Калькулятором (Пункт 11б). За неимением Экселя используйте приближенную формулу Уилсона-Гильферти:
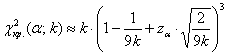 , где
, где ![]() отыскивается из соотношения
отыскивается из соотношения ![]() .
.
Сейчас для интереса проверил – погрешность составила всего одну сотую!
Гипотеза о равенстве генеральных дисперсий двух нормальных распределений
Две средние мы уже сравнивали, очередь за дисперсиями. Из двух нормальных ген. совокупностей извлечены независимые выборки объёмом ![]() и
и ![]() и найдены их исправленные дисперсии:
и найдены их исправленные дисперсии: ![]() и
и ![]() соответственно. Совершенно понятно, что эти значения случайны и отличны друг от друга. Но возникает вопрос: значимо или незначимо это отличие? Для ответа на этот вопрос на уровне значимости
соответственно. Совершенно понятно, что эти значения случайны и отличны друг от друга. Но возникает вопрос: значимо или незначимо это отличие? Для ответа на этот вопрос на уровне значимости ![]() проверяется гипотеза о равенстве генеральных дисперсий
проверяется гипотеза о равенстве генеральных дисперсий ![]() . Если она будет принята, то различие между выборочными значениями
. Если она будет принята, то различие между выборочными значениями ![]() объяснимо случайными факторами.
объяснимо случайными факторами.
Для проверки этой гипотезы используют критерий ![]() , где
, где ![]() – бОльшая исправленная дисперсия, а
– бОльшая исправленная дисперсия, а ![]() – мЕньшая.
– мЕньшая.
Данная случайная величина имеет распределение Фишера-Снедекора (так называемое F-распределение) со степенями свободы ![]() , если
, если ![]() или
или ![]() , если
, если ![]() . То есть, степень свободы
. То есть, степень свободы ![]() соответствует выборке с бОльшей исправленной дисперсией.
соответствует выборке с бОльшей исправленной дисперсией.
В качестве альтернативы рассматривают одну из следующих гипотез:
1) ![]() (если
(если ![]() ) либо
) либо ![]() (если
(если ![]() ). Для этой гипотезы строят правостороннюю критическую область:
). Для этой гипотезы строят правостороннюю критическую область:

Критическое значение ![]() можно найти по таблице критических значений F-распределения, а ещё лучше – с помощью стандартной функции Экселя, используйте тот же Калькулятор (Пункт 12).
можно найти по таблице критических значений F-распределения, а ещё лучше – с помощью стандартной функции Экселя, используйте тот же Калькулятор (Пункт 12).
2) ![]() – для этой гипотезы строится двусторонняя критическая область:
– для этой гипотезы строится двусторонняя критическая область:

Однако для решения нашей задачи достаточно найти лишь правое критическое значение ![]() .
.
Дело в том, что ![]() , и поэтому случайное значение
, и поэтому случайное значение ![]() (бОльшее единицы) заведомо не может попасть в левый кусок критической области.
(бОльшее единицы) заведомо не может попасть в левый кусок критической области.
Далее на основании выборочных данных рассчитывается наблюдаемое значение критерия ![]() , и если оно попадает в критическую область (
, и если оно попадает в критическую область (![]() для обоих случаев), то гипотеза
для обоих случаев), то гипотеза ![]() отвергается. Если
отвергается. Если ![]() , то принимается.
, то принимается.
Рассматриваемая гипотеза часто возникает, когда требуется сравнить точность двух приборов, инструментов, станков, двух методов исследования. И сейчас мы разберём эту стандартную задачу:
Пример 47
Некоторая физическая величина измерена ![]() и
и ![]() раз двумя различными способами. По результатам измерений найдены соответствующие погрешности
раз двумя различными способами. По результатам измерений найдены соответствующие погрешности ![]() . Требуется на уровне значимости 0,05 проверить, одинаковую ли точность обеспечивают эти способы измерений.
. Требуется на уровне значимости 0,05 проверить, одинаковую ли точность обеспечивают эти способы измерений.
Ситуации тут могут быть разные: это измерение двумя однотипными инструментами (например, двумя линейками), или инструментами разными (например, линейкой и штангенциркулем), или речь вообще идёт о двух методах измерения (например, с зажмуренным левым и правым глазом).
И возникает вопрос: различие между ![]() случайно или обусловлено тем, что какой-то способ точнее?
случайно или обусловлено тем, что какой-то способ точнее?
Решение: полагая, что погрешности измерений распределены нормально, проверим гипотезу ![]() о том, что точность двух способов одинакова против конкурирующей гипотезы
о том, что точность двух способов одинакова против конкурирующей гипотезы ![]() (она правдоподобнее, нежели
(она правдоподобнее, нежели ![]() ).
).
Для проверки гипотезы используем критерий ![]() , где
, где ![]() – бОльшая исправленная дисперсия, а
– бОльшая исправленная дисперсия, а ![]() – мЕньшая.
– мЕньшая.
Найдём критическое значение ![]() . Степень свободы
. Степень свободы ![]() должна соответствовать выборке с бОльшей дисперсией, следовательно,
должна соответствовать выборке с бОльшей дисперсией, следовательно, ![]() и
и ![]() . По соответствующей таблице либо с помощью Калькулятора (Пункт 12) находим:
. По соответствующей таблице либо с помощью Калькулятора (Пункт 12) находим:
![]()
При ![]() нулевая гипотеза принимается, а при
нулевая гипотеза принимается, а при ![]() (в критической области) – отвергается.
(в критической области) – отвергается.
Вычислим наблюдаемое значение критерия:
![]() , поэтому на уровне значимости 0,05 нет оснований отвергать гипотезу
, поэтому на уровне значимости 0,05 нет оснований отвергать гипотезу ![]() . Иными словами, различие выборочных значений
. Иными словами, различие выборочных значений ![]() обусловлено случайными факторами, но прежде всего, малым количеством опытов.
обусловлено случайными факторами, но прежде всего, малым количеством опытов.
Так, если бы было проведено в 10 раз больше измерений ![]() и получены те же самые погрешности, то
и получены те же самые погрешности, то ![]() , и гипотеза о равенстве ген. дисперсий уже отвергается. То есть здесь расхождение между
, и гипотеза о равенстве ген. дисперсий уже отвергается. То есть здесь расхождение между ![]() уже нельзя объяснить случайностью, а объяснимо оно именно тем, что второй способ менее точный (справедлива гипотеза
уже нельзя объяснить случайностью, а объяснимо оно именно тем, что второй способ менее точный (справедлива гипотеза ![]() ).
).
Ответ: на уровне значимости 0,05 точность способов измерения одинакова.
Творческая задача для самостоятельного решения, случай из жизни:
Пример 48
Две группы студентов-первокурсников написали контрольную по математическому анализу со следующими результатами:
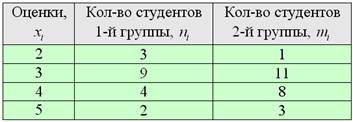
Предполагая, что успеваемость студентов распределена нормально, на уровне значимости 0,1:
1) Проверить гипотезу ![]() – о том, что группы однородны по составу (в плане соотношения лучше и хуже успевающих студентов) против конкурирующей гипотезы
– о том, что группы однородны по составу (в плане соотношения лучше и хуже успевающих студентов) против конкурирующей гипотезы ![]() ,
,
и в случае однородности групп обещанный пунктик:
2) Проверить гипотезу ![]() – об одинаковой успеваемости групп против гипотезы о том, что одна из групп более слабая.
– об одинаковой успеваемости групп против гипотезы о том, что одна из групп более слабая.
Вспоминаем, что такое дискретный вариационный ряд и как рассчитываются его характеристики. Не позволяй душе лениться! – в жизни пригодится, все числа уже в Экселе.
Ну что, порешаем ещё задачки? …конечно, порешаем! – ведь я маньяк в лучшем смысле этого слова:
Гипотеза о вероятности события
Пусть в достаточно большом количестве ![]() независимых испытаний некоторое случайное событие появилось
независимых испытаний некоторое случайное событие появилось ![]() раз, и есть основание полагать, что вероятность
раз, и есть основание полагать, что вероятность ![]() появления этого события (в каждом испытании) равна некоторому значению
появления этого события (в каждом испытании) равна некоторому значению ![]() . Возникает вопрос: значимо или незначимо отличается относительная частота
. Возникает вопрос: значимо или незначимо отличается относительная частота ![]() от этого гипотетического значения?
от этого гипотетического значения?
Для проверки гипотезы ![]() используют критерий
используют критерий 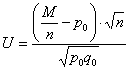 , где
, где ![]() , а
, а ![]() – случайное количество испытаний, в которых событие появилось. При этом для качественного результата должно выполняться неравенство
– случайное количество испытаний, в которых событие появилось. При этом для качественного результата должно выполняться неравенство ![]() .
.
Далее технически всё похоже на гипотезу о генеральной средней. Для конкурирующей гипотезы ![]() строится левосторонняя критическая область, для
строится левосторонняя критическая область, для ![]() – правосторонняя и для
– правосторонняя и для ![]() – двусторонняя:
– двусторонняя:
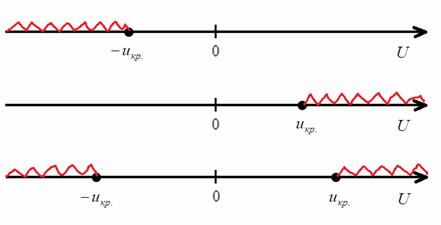
Критическое значение отыскивается из соотношения ![]() для односторонней области и
для односторонней области и ![]() – для двусторонней, где
– для двусторонней, где ![]() – выбранный уровень значимости, а
– выбранный уровень значимости, а ![]() – функция Лапласа.
– функция Лапласа.
Если наблюдаемое значение критерия 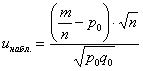 попадает в критическую область, то гипотеза
попадает в критическую область, то гипотеза ![]() отвергается.
отвергается.
Пример 49
В результате длительных наблюдений установлено, что вероятность полного выздоровления больного, принимавшего лекарство ![]() , равна 0,8. Новое лекарство
, равна 0,8. Новое лекарство ![]() назначено 800 больным, причём 660 из них полностью выздоровели. Можно ли считать новое лекарство значимо эффективнее лекарства
назначено 800 больным, причём 660 из них полностью выздоровели. Можно ли считать новое лекарство значимо эффективнее лекарства ![]() на пятипроцентном уровне значимости?
на пятипроцентном уровне значимости?
Итак, в результате использования нового лекарство получена относительная частота полного выздоровления ![]() и возникает вопрос: этот результат случаен или лекарство
и возникает вопрос: этот результат случаен или лекарство ![]() действительно эффективнее? Проясним эту ситуацию статистическим методом:
действительно эффективнее? Проясним эту ситуацию статистическим методом:
Решение: на уровне значимости ![]() проверим гипотезу
проверим гипотезу ![]() о том, что новое лекарство имеет такую же эффективность против конкурирующей гипотезы
о том, что новое лекарство имеет такую же эффективность против конкурирующей гипотезы ![]() , что оно более эффективно. Используем критерий
, что оно более эффективно. Используем критерий 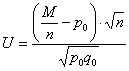 , где
, где ![]() – случайное количество пациентов из
– случайное количество пациентов из ![]() , которые полностью выздоровеют.
, которые полностью выздоровеют.
Критическое значение правосторонней критической области найдём из соотношения ![]() , в данном случае
, в данном случае
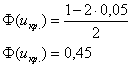
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*), определяем, что этому значению функции соответствует аргумент ![]() .
.
При ![]() нулевая гипотеза принимает, а при
нулевая гипотеза принимает, а при ![]() – отвергается:
– отвергается:
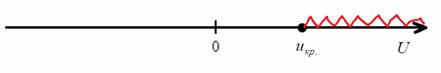
Вычислим ![]() и наблюдаемое значение критерия:
и наблюдаемое значение критерия:
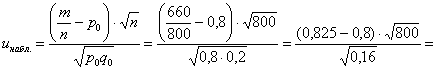
![]() , поэтому на уровне значимости 0,05 гипотезу
, поэтому на уровне значимости 0,05 гипотезу ![]() отвергаем в пользу конкурирующей гипотезы
отвергаем в пользу конкурирующей гипотезы ![]() . Таким образом, выборочный результат
. Таким образом, выборочный результат ![]() вряд ли объясним случайностью.
вряд ли объясним случайностью.
Ответ: на пятипроцентном уровне значимости новое лекарство эффективнее лекарства ![]() .
.
Самостоятельно:
Пример 50
Завод рассылает рекламные каталоги возможным заказчикам. Как показал опыт, вероятность того, что организация, получившая каталог, закажет рекламируемое изделие, равна 0,08. Завод разослал 1000 каталогов новой улучшенной формы и получил 98 заказов. Можно ли считать, что новая форма рекламы значимо эффективнее?
Примите уровень значимости ![]() и проверьте это предположение.
и проверьте это предположение.
И заключительный параграф этой интереснейшей статьи:
Сравнение вероятностей двух биномиальных распределений
На самом деле о вероятности биномиального распределения речь уже шла в предыдущей гипотезе, и теперь перед нами стоит задача сравнить вероятности двух биномиальных распределений.
Пусть в двух генеральных совокупностях проводятся независимые испытания, в каждом из которых событие ![]() может появиться – с неизвестной вероятностью
может появиться – с неизвестной вероятностью ![]() в первой совокупности и с неизвестной вероятностью
в первой совокупности и с неизвестной вероятностью ![]() – во второй. По выборочным сериям испытаний объёмами
– во второй. По выборочным сериям испытаний объёмами ![]() и
и ![]() найдены соответствующие относительные частоты:
найдены соответствующие относительные частоты:
![]() , где
, где ![]() – фактическое число появлений события
– фактическое число появлений события ![]() в 1-й и во 2-й выборке.
в 1-й и во 2-й выборке.
Требуется оценить, значимо или незначимо отличаются друг от друга относительные частоты. Незначимое отличие объяснимо случайными факторами и справедливостью гипотезы ![]() .
.
Для проверки этой гипотезы используют критерий:
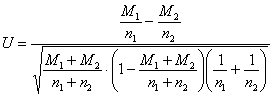 , где
, где ![]() – случайное количество появлений события
– случайное количество появлений события ![]() в 1-й и во 2-й выборке соответственно.
в 1-й и во 2-й выборке соответственно.
В качестве альтернативы рассматривают гипотезу ![]() либо
либо ![]() . Критические области строятся точно так же, как и в предыдущем пункте! Кстати, почему здесь можно использовать лапласовские соотношения? А дело в том (кто помнит), что при достаточно большой выборке биномиальное распределение близкО к нормальному.
. Критические области строятся точно так же, как и в предыдущем пункте! Кстати, почему здесь можно использовать лапласовские соотношения? А дело в том (кто помнит), что при достаточно большой выборке биномиальное распределение близкО к нормальному.
Возвращаемся к нашим помидорам:
Пример 51
От двух поставщиков в магазин поступило ![]() и
и ![]() однотипных изделий. В первой партии оказалось
однотипных изделий. В первой партии оказалось ![]() бракованных изделий, а во второй –
бракованных изделий, а во второй – ![]() . Требуется на уровне значимости 0,05 оценить, одинаково ли хороши поставщики.
. Требуется на уровне значимости 0,05 оценить, одинаково ли хороши поставщики.
Очевидно, что здесь существуют вполне конкретные вероятности ![]() – того, что магазин получит бракованное изделие от 1-го и 2-го поставщика соответственно. И эти вероятности нам не известны. Однако в нашем распоряжении есть выборочные данные – относительные частоты:
– того, что магазин получит бракованное изделие от 1-го и 2-го поставщика соответственно. И эти вероятности нам не известны. Однако в нашем распоряжении есть выборочные данные – относительные частоты:
![]()
И возникает вопрос: эта разница случайна или нет?
Решение: на уровне значимости ![]() проверим гипотезу
проверим гипотезу ![]() о том, что поставщики равноценны против конкурирующей гипотезы
о том, что поставщики равноценны против конкурирующей гипотезы ![]() .
.
Критическое значение двусторонней критической области найдём из соотношения ![]() . В данном случае:
. В данном случае:
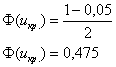
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем ![]() . При
. При ![]() нулевая гипотеза принимается, а при
нулевая гипотеза принимается, а при ![]() – отвергается:
– отвергается:

Вычислим наблюдаемое значение критерия:
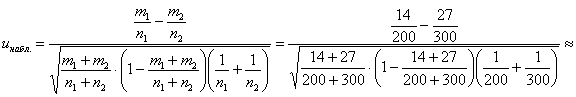
![]() – полученное значение попало в область принятия гипотезы
– полученное значение попало в область принятия гипотезы ![]() , таким образом, различие относительных частот
, таким образом, различие относительных частот ![]() , скорее всего, случайно.
, скорее всего, случайно.
Ответ: на уровне значимости 0,05 нет оснований отдавать предпочтение какому-то одному из поставщиков
Как говорится, что там помидоры, что там.
И почётное право завершить этот урок предоставляется героям, которые помогали нам на протяжении всего курса тервера, ну а может и некоторые читатели уже взялись за оружие:))
Пример 52
Два стрелка совершили по 50 выстрелов в цель. Первый стрелок поразил цель 41 раз, а второй – 36. Можно ли на уровне значимости 0,1 утверждать, что первый стрелок более меткий?
Решение и ответ совсем близко.
Но и это ещё не всё! На очереди важнейшая и очень распространённая гипотеза о законе распределения генеральной совокупности.
До скорых встреч!
Решения и ответы:
Пример 41. Решение: по условию, известны генеральные дисперсии, поэтому для проверки гипотезы используем критерий 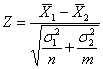 .
.
а) Для гипотезы ![]() строим левостороннюю критическую область. Критическое значение найдём из соотношения
строим левостороннюю критическую область. Критическое значение найдём из соотношения ![]() . Для уровня значимости
. Для уровня значимости ![]() :
:
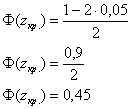
По таблице значений функции Лапласа определяем ![]() . Таким образом, при
. Таким образом, при ![]() нулевую гипотезу принимаем, а при
нулевую гипотезу принимаем, а при ![]() (в критической области) – отвергаем:
(в критической области) – отвергаем:
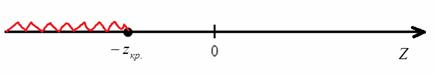
Вычислим наблюдаемое значение критерия:
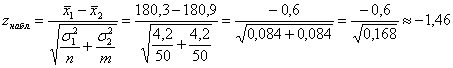
![]() , поэтому на уровне значимости 0,05 нулевую гипотезу принимаем.
, поэтому на уровне значимости 0,05 нулевую гипотезу принимаем.
б) Для гипотезы ![]() строим двустороннюю критическую область:
строим двустороннюю критическую область:

Критическое значение найдём из соотношения ![]() :
:
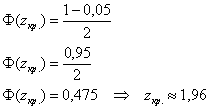
Наблюдаемое значение критерия ![]() попало в область принятия гипотезы
попало в область принятия гипотезы ![]() , поэтому на уровне значимости 0,05 нулевую гипотезу принимаем.
, поэтому на уровне значимости 0,05 нулевую гипотезу принимаем.
Ответ: в обоих случаях гипотезу ![]() принимаем.
принимаем.
Напоминаю, что это не 100%-ное доказательство гипотезы, т.к. существует ![]() -вероятность того, что мы приняли неверную гипотезу (совершили ошибку второго рода).
-вероятность того, что мы приняли неверную гипотезу (совершили ошибку второго рода).
Пример 44. Решение: рассмотрим случайную величину ![]() , где
, где ![]() – случайные значения выборочных средних, и проверим гипотезу
– случайные значения выборочных средних, и проверим гипотезу ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() . Поскольку генеральная дисперсия этой случайной величины не известна, то используем критерий
. Поскольку генеральная дисперсия этой случайной величины не известна, то используем критерий ![]() , распределённый по закону Стьюдента с количеством степеней свободы
, распределённый по закону Стьюдента с количеством степеней свободы ![]() .
.
Для уровня значимости ![]() и
и ![]() по таблице критических точек распределения Стьюдента находим критическое значение для двусторонней критической области:
по таблице критических точек распределения Стьюдента находим критическое значение для двусторонней критической области:
![]()
Таким образом, при ![]() нулевую гипотезу принимаем, и вне этого интервала (в критической области) отвергаем:
нулевую гипотезу принимаем, и вне этого интервала (в критической области) отвергаем:
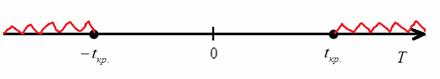
Найдём наблюдаемое значение критерия. Для этого нужно вычислить выборочную среднюю разницу ![]() между выборочными средними
между выборочными средними ![]() и
и ![]() и соответствующую дисперсию
и соответствующую дисперсию ![]() . Заполним расчётную таблицу:
. Заполним расчётную таблицу:
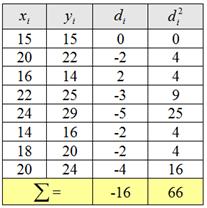
Таким образом:

Наблюдаемое значение критерия:
![]() – полученное значение попало в критическую область, поэтому на уровне значимости 0,05 гипотезу
– полученное значение попало в критическую область, поэтому на уровне значимости 0,05 гипотезу ![]() отвергаем.
отвергаем.
Ответ: на уровне значимости 0,05 результаты лабораторий отличны друг от друга.
Пример 46. Решение: полагая, что погрешности размера выпускаемых изделий распределены нормально, проверим гипотезу ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() . Используем критерий
. Используем критерий ![]() .
.
Так как в конкурирующей гипотезе речь идёт о бОльших значениях дисперсии, то критическая область будет правосторонней. Найдём критическое значение. Для уровня значимости ![]() и количества степеней свободы
и количества степеней свободы ![]() с помощью MS Excel находим критическое значение:
с помощью MS Excel находим критическое значение:
![]()
При ![]() нулевая гипотеза принимается, а при
нулевая гипотеза принимается, а при ![]() – отвергается.
– отвергается.
Вычислим наблюдаемое значение критерия:
![]() , поэтому на уровне значимости 0,05 гипотезу
, поэтому на уровне значимости 0,05 гипотезу ![]() отвергаем.
отвергаем.
Иными словами, выборочный результат ![]() статистически значимо отличается от нормативного значения 0,2, и оборудование, на котором производятся изделия, нуждается в регулировке. Скорее всего.
статистически значимо отличается от нормативного значения 0,2, и оборудование, на котором производятся изделия, нуждается в регулировке. Скорее всего.
Ответ: на уровне значимости 0,05 партию изделий принять нельзя.
Пример 48. Решение: Заполним расчётную таблицу:
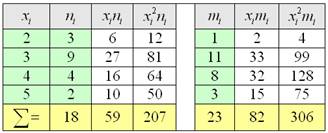
Вычислим выборочные характеристики. Средний балл:
![]()
Выборочные дисперсии:
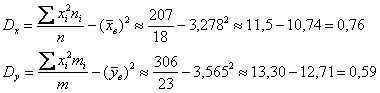
Исправленные дисперсии:
![]()
1) На уровне значимости 0,1 проверим гипотезу ![]() против конкурирующей гипотезы
против конкурирующей гипотезы ![]() . Используем критерий
. Используем критерий ![]() , где
, где ![]() – бОльшая исправленная дисперсия, а
– бОльшая исправленная дисперсия, а ![]() – меньшая.
– меньшая.
Найдём правое критическое значение двусторонней критической области. Для уровня значимости ![]() и числа степеней свободы
и числа степеней свободы ![]() с помощью MS Excel находим:
с помощью MS Excel находим:
![]()
Вычислим наблюдаемое значение критерия:
![]() , поэтому на уровне значимости 0,1 гипотезу
, поэтому на уровне значимости 0,1 гипотезу ![]() принимаем. Таким образом, группы однородны (в плане соотношения лучше и хуже успевающих студентов).
принимаем. Таким образом, группы однородны (в плане соотношения лучше и хуже успевающих студентов).
Замечание: здесь, конечно, речь идёт не о строгом, а о примерном равенстве генеральных дисперсий.
2) На уровне значимости 0,1 проверим гипотезу ![]() против гипотезы
против гипотезы ![]() о том, что 1-я группа учится слабее. Исследуемые совокупности достаточно малы
о том, что 1-я группа учится слабее. Исследуемые совокупности достаточно малы ![]() и их генеральные дисперсии неизвестны, но в предыдущем пункте статистически обосновано незначимое различие ген. дисперсий. Поэтому для проверки гипотезы можно использовать критерий
и их генеральные дисперсии неизвестны, но в предыдущем пункте статистически обосновано незначимое различие ген. дисперсий. Поэтому для проверки гипотезы можно использовать критерий 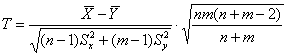 , где
, где ![]() – случайные значения выборочных средних, а
– случайные значения выборочных средних, а ![]() – соответствующие исправленные выборочные дисперсии.
– соответствующие исправленные выборочные дисперсии.
Поскольку конкурирующая гипотеза имеет вид ![]() , то критическая область будет левосторонней. Для уровня значимости
, то критическая область будет левосторонней. Для уровня значимости ![]() и числа степеней свободы
и числа степеней свободы ![]() найдём критическое значение односторонней области:
найдём критическое значение односторонней области:
![]() (Калькулятор - Пункт 10в)
(Калькулятор - Пункт 10в)
При ![]() нулевая гипотеза отвергается, а при
нулевая гипотеза отвергается, а при ![]() – принимается:
– принимается:
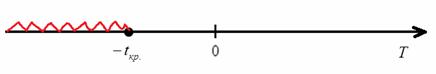
Вычислим наблюдаемое значение критерия:
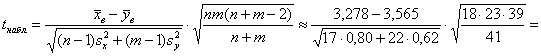
 , поэтому на уровне значимости 0,1 нет оснований отвергать гипотезу
, поэтому на уровне значимости 0,1 нет оснований отвергать гипотезу ![]() .
.
Таким образом, по результатам контрольной работы нельзя утверждать, что различие между средними оценками ![]() обусловлено тем, что 1-я группа более слабая. Для проверки этого предположения требуется дальнейший мониторинг за успеваемостью.
обусловлено тем, что 1-я группа более слабая. Для проверки этого предположения требуется дальнейший мониторинг за успеваемостью.
Ответ: на уровне значимости 0,1 нет оснований отвергнуть нулевые гипотезы.
Пример 50. Решение: на уровне значимости ![]() проверим гипотезу
проверим гипотезу ![]() о том, новая рекламная кампания имеет такую же эффективность против конкурирующей гипотезы
о том, новая рекламная кампания имеет такую же эффективность против конкурирующей гипотезы ![]() . Используем критерий
. Используем критерий 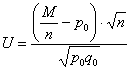 , где
, где ![]() , а
, а ![]() – случайное кол-во заказов, которое может поступить в результате рассылки 1000 новых каталогов.
– случайное кол-во заказов, которое может поступить в результате рассылки 1000 новых каталогов.
Найдём критическое значение правосторонней критической области:
![]() , по таблице значений функции Лапласа определяем
, по таблице значений функции Лапласа определяем ![]() . При
. При ![]() нулевую гипотезу принимаем, а при
нулевую гипотезу принимаем, а при ![]() – отвергаем.
– отвергаем.
Вычислим наблюдаемое значение критерия:
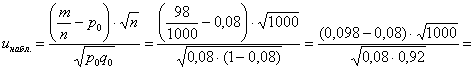
![]() , поэтому на уровне значимости
, поэтому на уровне значимости ![]() гипотезу
гипотезу ![]() отвергаем.
отвергаем.
Ответ: на уровне значимости 0,05 новая форма рекламы значимо эффективнее.
Пример 52. Решение: на уровне значимости ![]() проверим гипотезу
проверим гипотезу ![]() против гипотезы
против гипотезы ![]() о том, что 1-й стрелок стреляет точнее.
о том, что 1-й стрелок стреляет точнее.
Найдём критическое значение правосторонней критической области:
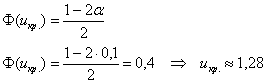
При ![]() нулевую гипотезу принимаем, а при
нулевую гипотезу принимаем, а при ![]() – отвергаем.
– отвергаем.
Вычислим наблюдаемое значение критерия:
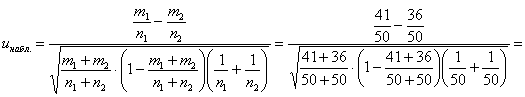
![]() , следовательно, на уровне значимости 0,1 нет оснований отвергать гипотезу
, следовательно, на уровне значимости 0,1 нет оснований отвергать гипотезу ![]() .
.
Ответ: на уровне значимости 0,1 нет оснований считать, что 1-й стрелок более меткий.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright