Как привести уравнение линии второго порядка
к каноническому виду?

Задача приведения уравнения линии 2-го порядка к каноническому виду следовала за нами практически с самого начала изучения темы и сейчас мы окончательно разберёмся, как общее уравнение линии второго порядка (здесь и далее подразумевается, что не равны одновременно нулю) свести к одному из девяти канонических случаев.

В статьях об эллипсе, гиперболе и параболе, а также на практикуме Задачи с линиями второго порядка очень подробно отработан частный случай уравнения, когда коэффициент :

Пожалуйста, внимательно посмотрите на своё уравнение, которое вам нужно привести к каноническому виду – есть ли в нём слагаемое, которое содержит произведение ?

Если такого слагаемого нет, то вам хватит материалов перечисленных выше уроков.

Если же такое слагаемое есть – то не хватит =)

Как многие подметили, члены общего уравнения «отвечают» за параллельный перенос линии, который имеет место, когда хотя бы один из коэффициентов отличен от нуля. И логично предположить, что ненулевое слагаемое «отвечает» за поворот линии. Исключение составляет угол в 90 градусов (а также любой кратный ему угол, например ), при повороте на который мы отделываемся лёгким испугом, укладываясь в рамки хорошо отшлифованного частного случая .

Уравнение с ненулевым коэффициентом «бэ» неприятно тем, что в общем случае его невозможно привести к каноническому виду с помощью обычных средств алгебры: переноса слагаемых, их группировки, вынесений за скобки, выделения полных квадратов и прочей школьной самодеятельности. Поэтому на помощь приходится привлекать более мощные методы решения.

Рассмотрим в качестве примера уравнение . Какие будут идеи? …Да ладно с ними, с идеями, тут даже не понятно, какую линию оно задаёт. Эллипс? Гиперболу? Параболу? Что-то другое из классификации?

Немного потраченного времени, и вы научитесь довольно легко находить ответы на эти вопросы, в частности, без особых проблем сможете определить, что данное уравнение определяет эллипс с полуосями , который расположен центром в точке и повёрнут относительного своего канонического положения на отрицательный угол, составляющий примерно :
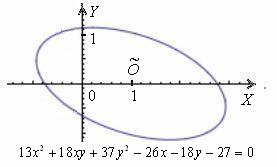
Эллипс в неканоническом положении
Мысленно возьмите эллипс в руки, поверните его на любой угол и переместите в произвольное место плоскости. Новому положению эллипса будет соответствовать совершенно другое уравнение, и если вам предъявить его без чертежа, то никто в жизнь не догадается, что оно определяет тот же самый эллипс. Именно поэтому и появилась задача приведения уравнения к каноническому виду – чтобы независимо от расположения линии выяснить, что это за зверь и каким нравом он обладает.

На предыдущих уроках я рассматривал два способа приведения. Применительно к нашему примеру:

1) Повернём эллипс на (против часовой стрелки) вокруг точки и осуществим его параллельный перенос центром в начало координат. В результате получится нужное уравнение .

2) Перейдём к прямоугольной системе координат , которая получается путём поворота исходной системы координат на вокруг начала координат и её параллельного переноса центром в точку . Таким образом, в новой системе координат уравнение данного эллипса запишется в каноническом виде: .

Прошу прощения за невысокое качество и точность чертежей данной статьи:
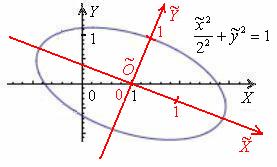
Поворот и параллельный перенос прямоугольной системы координат
Навскидку второй способ кажется вычурным и неуклюжим, однако, если немного призадуматься, то он более корректен. И толстый намёк на это уже проскочил чуть выше: куда бы мы ни переместили данную линию, какую бы систему координат ни выбрали – эллипс останется тем же самым эллипсом с полуосями , своими фокусами и другими индивидуальными характеристиками.

У многих читателей в пределах досягаемости находится учебник по высшей математике. Пусть это будет его каноническое положение в исходной системе координат. Книгу можно положить на стол, на стул, на кровать, под кровать, в мусорное ведро – да куда угодно. Но учебник останется при этом тем же самым учебником.

То есть с позиций математики, координатная сетка относительна и вторична по отношению к тому или иному объекту. Следовательно, вполне логично и правомерно тревожить именно систему координат, а не «уникальный» эллипс, учебник или что-то ещё. Конечно, с точки зрения физики положение тела имеет большое значение,… …пожалуй, сверну комментарий, а то сейчас набегут любители философии и устроят дискуссию =)

Суть преамбулы состоит в том, что на данном уроке мы будем приводить уравнение линии 2-го порядка путём перехода к новой прямоугольной системе координат, в которой уравнение исследуемой линии примет канонический вид.

Существует несколько практических методов приведения уравнения линии к каноническому виду, причём, некоторые из них являются достаточно трудными. Я постараюсь составить максимально простой конспект, доступный человеку с любым уровнем подготовки.

Все линии 2-го порядка можно разделить на две большие группы:

1) центральные линии, обладающие единственным центром (точкой) симметрии (эллипс, мнимый эллипс, гипербола, пара мнимых или действительных пересекающихся прямых);

2) нецентральные линии, у которых центры симметрии отсутствуют (парабола) либо их бесконечно много (пара действительных или мнимых параллельных прямых, пара совпавших прямых).

Итак, вы счастливый обладатель общего уравнения с ненулевым коэффициентом . С чего начать? На первом шаге целесообразно выяснить, к какой группе относится линия. Для этого нужно мысленно либо на черновике составить и вычислить определитель . Если , то перед нами уравнение центральной линии, если же – то нецентральной.

Для уравнения :
, значит, оно определяет центральную линию.

Зачем это нужно? Чтобы подобрать наиболее выгодный способ решения. Конечно, если ваш преподаватель требует строго придерживаться определённого шаблона, то ничего не поделать…. Тем не менее, я постараюсь провести вас самой комфортной и короткой тропинкой через дебри.

Для приведения уравнения центральной линии, по моему мнению, лучше всего использовать метод инвариантов. Но, к сожалению, он перестаёт работать в нецентральном случае, поэтому на помощь придётся привлечь достаточно трудоёмкий универсальный способ решения либо ортогональное преобразование квадратичной формы (однако тут уже нужно ориентироваться в другой теме). Сначала разберём одно, затем другое, и даже если вам нужно разобраться только с нецентральной линией, постарайтесь не пропускать первый параграф, поскольку вся информация взаимосвязана:

Приведение уравнения центральной линии. Метод инвариантов

Во-первых, разберёмся с термином. Инвариант – это величина, которая остаётся неизменной при тех или иных преобразованиях.

Простейший пример геометрического инварианта – это длина отрезка относительно его параллельного переноса. В результате данного преобразовании меняются координаты концов отрезка, но его длина остаётся неизменной (инвариантной).

В частности, длина и ширина учебника по высшей математике (который можно положить на стол, на стул, на кровать, под кровать, в мусорное ведро) – это инварианты относительно перемещения книги в пространстве. А вот если ненавистный томик… чего студент боится больше всего? …матана порвать в клочья, то его размеры уже перестанут быть инвариантами относительно этих механических повреждений =) Но инвариантом останется сам математический анализ. Так что рви, не рви, а осваивать его придётся =)

Однако вернёмся к нашему демонстрационному уравнению . Очевидно, что можно выбрать бесконечно много других прямоугольных систем координат и получить бесконечно много разных уравнений вида , которые задают один и тот же эллипс. И возникает вопрос: а есть ли у этого множества уравнений что-то одинаковое, характерное только для данной линии? Иными словами, есть ли инварианты?

Да, есть! Если уравнение линии 2-го порядка задано общим видом в некоторой прямоугольной системе координат, то инвариантами относительно поворота и параллельного переноса прямоугольной системы координат являются следующие ЧИСЛА:

– сумма коэффициентов при

старый знакомец:

и ещё один определитель:

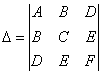
Рассмотрим общее уравнение линии 2-го порядка и поставим задачу подобрать новую прямоугольную систему координат ТАК, чтобы уравнение данной линии приняло вид (который элементарно сводится к канонической форме). Заметим попутно логичную вещь – коэффициенты итогового уравнения, «отвечающие» за поворот и параллельный перенос равны нулю:

Поскольку инварианты (числа) НЕ ЗАВИСЯТ от коэффициентов того или иного уравнения, которым задана конкретная исследуемая линия, то справедливыми являются следующие равенства:

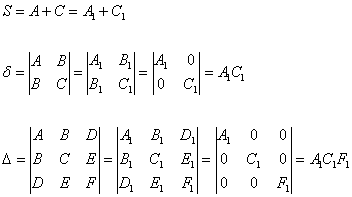
откуда следует простой и изящный алгоритм решения нашей задачи:

1) Из исходного уравнения находим числа .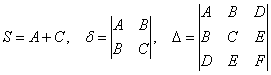
2) Решаем систему 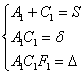и записываем уравнение , которое легко приводится к каноническому виду. При этом координаты нового начала координат отыскиваются как решение системы линейных уравнений 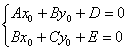, а угол «альфа» поворота новой системы координат относительно старой системы координат – из уравнения . В случае угол равен либо , либо , и это недостаток формулы. Но это не беда. Потому что есть другая формула: .

Таким образом, решение нашей задачи укладывается в стройную и понятную схему, доступную даже школьнику. Выясним же, наконец, как из потрёпанного уравнения получается канонический эллипс :

Пример 1

Привести уравнение линии второго порядка к каноническому виду

Найти начало соответствующей системы координат и угол её поворота

Решение: перейдём к новой прямоугольной системе координат , в которой уравнение данной линии примет вид .

На первом шаге из исходного уравнения находим коэффициенты .
В тетради это удобно сделать следующим образом:

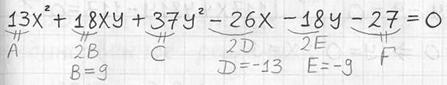
Здесь важно не потерять «минусы», а также не забыть разделить пополам нужные числа. Кроме того, некоторые слагаемые уравнения могут отсутствовать, и тогда соответствующие коэффициенты будут равны нулю – не спешим и не путаемся!

В нашем случае всё на месте и, соответственно, все коэффициенты ненулевые:

Вычислим инварианты:

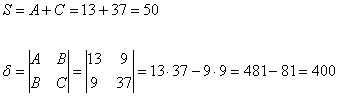
Последний определитель выгодно раскрыть с помощью элементарного преобразования, прибавив к третьей строке первую строку:

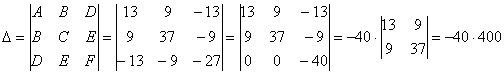
Инварианты найдёны, составим и решим систему:

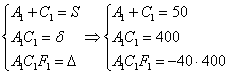
Из последних двух уравнений сразу просматривается значение коэффициента :
поскольку , то, подставляя это произведение в 3-е уравнение, получаем:

Но его обычно оставляют на закуску, тут важно разобраться с другими коэффициентами. Есть длинный путь, и есть короткий путь.

Путь длинный: из 1-го уравнения выражаем – подставляем во второе уравнение:

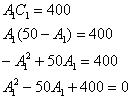
Решим квадратное уравнение:

В результате получается два комплекта симметричных корней:

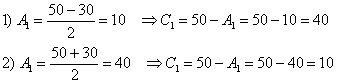
Путь короткий, к которому я рекомендую пристреляться, в том числе, и чайникам. Это подбор корней. Смотрим на первые два уравнения системы: 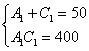. Прикидку можно делать либо по первому уравнению, либо по второму, кому как удобнее. Лично я привык ориентироваться по сумме коэффициентов. Правдоподобных вариантов здесь не так и много:
0 и 50
10 и 40 – удовлетворяет и первому и второму уравнению
20 и 30
30 и 20
40 и 10 – симметричная пара корней
50 и 0

Как видите, на подходящую пару чисел мы «натыкаемся» практически сразу. В силу симметричности уравнений решением будут являться и «зеркальные» значения 40 и 10.

Таким образом, в нашем распоряжении оказывается два набора корней:

Не забываем выполнить проверку, подставив значения первого (можно второго) комплекта в левую часть каждого уравнения системы:

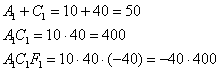
Получены соответствующие правые части исходных уравнений, что и требовалось проверить.

Теперь мысленно либо на черновике следует выяснить, какое решение приведёт нас к желаемому результату.

Подставляем в уравнение :

Техника завершающих преобразований хорошо знакома из предыдущих уроков об эллипсе, гиперболе и параболе:

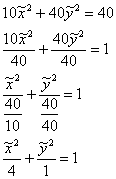
– эллипс с центром в точке , большой полуосью , малой полуосью .

Такой фразы будет достаточно – нас никто не спрашивал про фокусы, эксцентриситет и другие характеристики линии.

Всё вышло удачно с первой попытки. Если в уравнение подставить второй набор корней , то получится неканоническая запись того же эллипса – повернутого на 90 градусов. Случай такого поворота я рассмотрел ещё в ознакомительных материалах про эллипс.

Координаты начала новой системы координат найдём как решение системы:

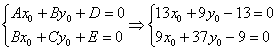
Первое уравнение умножим на 9, второе уравнение умножим на 13 и из 2-го уравнения почленно вычтем 1-е (проще способа не видно):

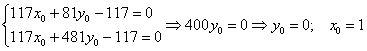
Таким образом:

Найдём угол поворота новой системы координат относительно старой:

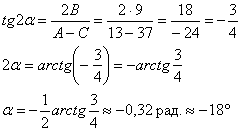
Или по второй, более лёгкой, но почему-то менее распространённой формуле:

В том случае если по условию необходимо выполнить чертёж – выполняем чертёж, приведённый в начале урока. Впрочем, мне нетрудно скопипастить:
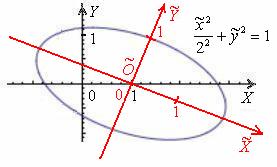
Итоговый чертёж задачи
Ввиду сложности чертежа вполне допустимо его схематичное оформление, однако всё-таки постарайтесь, чтобы рисунок был похож на правду.

В лайт-варианте можно изобразить только систему координат и эллипс в горизонтальном положении, но тогда могут возникнуть вопросы у преподавателя. Да, и ещё момент – при таких раскладах координаты центра запишутся в новой системе координат: , что вызовет дополнительную путаницу.

Ответ: – эллипс с полуосями – в системе координат с началом в точке , повёрнутой относительно исходной системы координат на угол .

Это мы рассмотрели так называемый эллиптический случай, когда коэффициенты – отличны от нуля и одного знака (оба положительны либо оба отрицательны), т. е. когда их произведение .

Но при таком раскладе может получиться не только эллипс. Если все три коэффициента одного знака, то получится мнимый эллипс. Условно говоря, если бы мы в рассмотренной задаче получили уравнение , то пришли бы к уравнению . Причём, весь алгоритм и порядок оформления остались бы прежними + приятный бонус – отсутствие чертежа, поскольку мнимый эллипс остаётся разве что мнить =)

Ещё одна разновидность эллиптического случая – нулевой свободный член: , предвестником которого является нулевой третий инвариант . И действительно, из 3-го уравнения системы следует, что если и , то нулю может быть равен только коэффициент «эф первое». Условно говоря, в нашей задаче получилось бы уравнение , которое легко сводится к пункту № 6 классификации линий 2-го порядка: – пара мнимых пересекающихся прямых с единственной действительной точкой их пересечения – с нулевыми координатами новой системы координат .

Предлагаю самостоятельно ознакомиться с гиперболическим случаем:

Пример 2

Привести уравнение линии второго порядка к каноническому виду

Найти начало соответствующей системы координат, угол её поворота и выполнить чертёж.

После краткого образца решения есть важные дополнительные комментарии.

Во второй части статьи рассмотрим параболический случай , где по очевидной причине метод инвариантов становится непригодным:

Приведение нецентральной линии к каноническому виду

Сейчас мы освоим универсальный метод решения, который приближен к соответствующему теоретическому материалу стандартного курса аналитической геометрии. Таким образом, разобранные ниже задачи помогут сориентироваться не только в практике, но и лучше понять теорию.

Классический алгоритм приведения уравнения к каноническому виду вкратце состоит в следующем:

На первом шаге выясняется угол поворота исходной линии относительно своего канонического положения и осуществляется поворот исходной системы координат на данный угол. В результате в новой прямоугольной системе координат уравнение исследуемой линии записывается в виде:

На втором шаге выделяются полные квадраты (при необходимости), и проводится параллельный перенос системы координат началом в нужную точку . После чего в итоговой прямоугольной системе координат получается уравнение , от которого до канонической формы рукой подать.

Должен отметить неудачные обозначения со штрихами, но так принято практически во всех учебниках, и сейчас я буду придерживаться стандарта (ну, или почти придерживаться), поскольку немалой части аудитории нужно сдавать теорию. Штрихи, как вы поняли, к производным функциям никакого отношения не имеют. В предыдущем параграфе я намеренно использовал обозначения вместо и чтобы не привить «чайникам» отвращение к теме.

Таким образом, универсальный способ приведения к линии 2-го порядка к каноническому виду предполагает два последовательных преобразования прямоугольной системы координат – поворот и параллельный перенос:

Как, наверное, все уже догадались и горестно вздохнули, удобный метод инвариантов позволял получить то же самое одним махом:

Но в параболическом случае мы вынуждены выехать с тихой просёлочной дороги метода инвариантов на оживлённую автостраду общего способа решения:

Пример 3

Привести уравнение линии второго порядка к каноническому виду

Выполнить чертёж.

Решение: в первую очередь выясним тип линии. Вычислим определитель, составленный из коэффициентов :

, значит, у нас нецентральная линия и это может быть или парабола, или пара параллельных прямых (действительных либо мнимых), или пара совпавших прямых.

1) Осуществим поворот исходной системы координат и переход к новой системе координат ТАК, чтобы получить уравнение вида (без слагаемого, «отвечающего» за поворот).

Искомый угол поворота найдём по формуле:
или

Внимание! Данная формула справедлива только для параболического случая ().

В нашем примере: .

Вообще говоря, очевиден корень , но здесь есть одна тонкость. Наверняка многие обратили внимание на тот факт, что если линию 2-го порядка (например, гиперболу) повернуть на 180 градусов, то она совпадёт сама с собой. Исключение составляет капризная парабола, ветви которой развернутся в противоположную сторону. А парабола у нас вполне может нарисоваться, поэтому, необходимо взять на заметку ещё один угол: , или, что то же самое: .

Продолжаем:

Если осуществляется поворот прямоугольной системы координат на произвольный угол «альфа» и переход к новой системе координат , то формулы перехода от старых координат к новым координатам аналитически выражается следующей системой:

, где «альфа» – угол данного поворота.

Из тригонометрических формул нетрудно выразить синус и косинус через известный нам тангенс, однако выражения получаются не однозначными:

И сложившейся ситуации вполне прагматичным решением будет привлечь на помощь метод научного тыка. Не теряя времени, начинаем работать непосредственно с углом «альфа» и используем формулы . В результате дальнейших действий может получиться неканоническое уравнение (а это возможно в единственном случае – когда исследуемое уравнение задаёт параболу и та оказывается развёрнутой в другую сторону). Тогда следует рассмотреть противоположный угол поворота системы координат, при этом значение тангенса угла останется тем же самым: , но формулы сменят знаки:
.

Итак, для угла выбираем первый комплект формул:

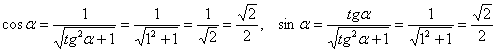
Подставим найденные (к слову, табличные) значения в аналитические выражения поворота :

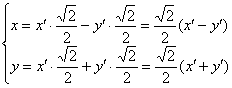
Теперь подставим и в исходное уравнение :

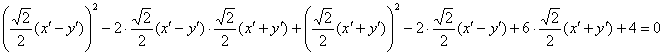
Нет причин в ужасе закрывать глаза ладонями – это ещё далеко не самое страшное, что может встретиться. Аккуратно-внимательно используем формулы сокращённого умножения, раскрываем скобки, приводим подобные слагаемые. И НЕ ТЕРЯЕМ ШТРИХИ:

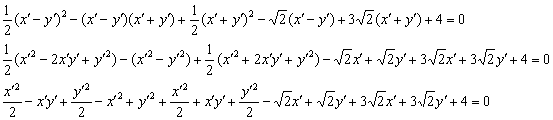
Очень многое взаимоуничтожается, и в первую очередь, конечно же, «убирается» поворот (слагаемое, содержащее произведение ):

По всем признакам получается как раз парабола. Сократим каждое слагаемое на 2 и перебросим некоторые из них в правую часть:

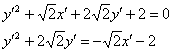
Перед слагаемым, содержащим «икс штрих», нарисовался знак минус, и это плохо. Для лучшего понимания я проиллюстрирую выполненные действия готовым чертежом:
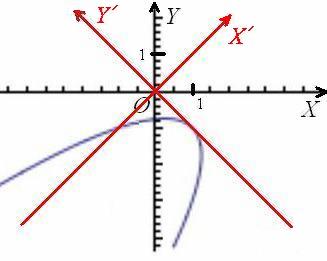
Парабола оказалась в неканоническом положении после поворота системы координат
В результате поворота исходной системы координат вокруг точки на 45 градусов, мы перешли от уравнения к уравнению в новой системе координат . Но загвоздка состоит в том, что ветви параболы направлены «в противоход» оси (наклоните головы влево на 45 градусов), о чём нам и сообщил знак «минус» при переменной нового уравнения.

Таким образом, выясняется, что поворот исходной системы координат следовало осуществить на угол . Ну что делать, не повезло, парабола запросто могла ведь «смотреть и в нужную сторону»….

Начинаем всё сначала. Тангенс правильного «кандидата» тоже равен единице, и мы подставляем значение в резервный комплект формул:

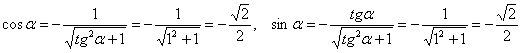
Подставим значения в уравнения поворота:

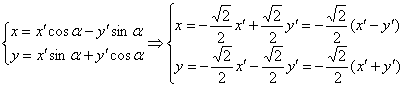
И, наконец, подставим в исходное уравнение :

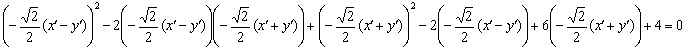
В качестве некоторой компенсации за наши мучения, для уравнения нецентральной линии существует эксклюзивная фишка, которую можно использовать как в целях самопроверки, так и по причине банальной лени. В результате рассматриваемой подстановки сумма упрощается до , где – старый знакомый инвариант. Таким образом, громоздкая сумма первых трёх слагаемых 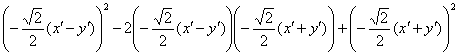превратится в :

Но при оформлении, конечно, желательно всё расписать подробно, как мы это сделали в ходе предыдущей неудачной попытки.

Доводим уравнение до кондиции:

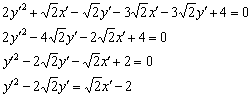
Ну вот, так бы сразу:
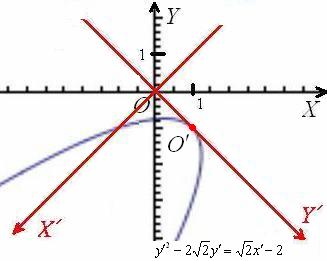
Корректный угол поворота
Проведём очередную разминку и заодно спасём от онемения пятую точку. Пожалуйста, встаньте лицом к монитору и наклонитесь вправо на 90 градусов. Теперь поверните голову ещё на 45 градусов в том же направлении и полюбуйтесь почти канонической параболой.

2) Осталось откалибровать уравнение до канонического вида параллельным переносом системы координат. Это значительно проще. Выделяем полный квадрат:

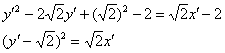
Таким образом, вершина параболы расположена в точке – ВНИМАНИЕ, это координаты точки в новой системе координат . В позе страуса с наклоном головы вправо на 135 градусов можно отчётливо разглядеть, что у вершины параболы именно такие координаты!

Путём параллельного переноса системы координат началом в точку перейдём к новой системе координат . Аналитически данное действие выражается заменами , в результате которых получается долгожданное каноническое уравнение:

Выполним окончательный чертёж. Оси совпали, но это воля случая:
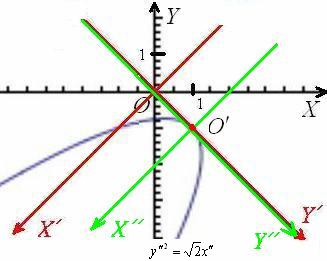
Поворот и параллельный перенос системы координат позволил привести уравнение к каноническому виду
Страусы одобряют =)

Ответ: данная линия представляет собой параболу, каноническое уравнение которой получается путём поворота системы координат вокруг своего начала на и её дальнейшим параллельным переносом в точку .

Существует ли способ проще? Существует! Изучайте квадратичные формы и урок об их ортогональном преобразовании, на котором решение этой задачи получилось заметно короче!

Также интересно отметить, что для параболы метод инвариантов, хоть и не работает, но тоже позволяет найти её каноническое уравнение. Во-первых, полезно запомнить характеристический признак: уравнение линии 2-го порядка, инварианты которого удовлетворяют условиям , задаёт параболу и только её.

Представьте, что вы видите уравнение в первый раз. Да… с оттенком черного юмора получилась фраза =) Выпишем коэффициенты и вычислим инварианты:

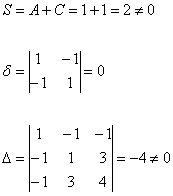
, следовательно, данное уравнение определяет именно параболу, а не какую-то другую линию.

И, во-вторых, найденные инварианты позволяют найти фокальный параметр параболы по формуле:

Таким образом:

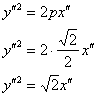
Желающие могут использовать данный путь для самопроверки или даже в качестве основного решения в критической ситуации – когда не получается найти уравнение параболы стандартным способом, но жизненно важно родить хоть что-то. Кроме того, нетрудно найти угол поворота, а там, глядишь, и прокатит.

Следующий пример для самостоятельной разработки:

Пример 4

Привести уравнение линии второго порядка к каноническому виду
, , ну и для желающих потренироваться я на кошках есть бессмертная классика: .

Выполнить чертёж, на котором отразить все преобразования системы координат.

Краткий алгоритм решения с повторением важных моментов чуть ниже, а примерный образец оформления задачи – в конце урока.

Следует отметить, что на практике достаточно популярна урезанная версия задачи. Случай, когда нужно выполнять только параллельный перенос, досконально изучен на предыдущих уроках, но бывает и так, что требуется осуществить только поворот системы координат.

Так, например, в уравнении отсутствуют слагаемые, «отвечающие» за параллельный перенос. Угол поворота системы координат находится элементарно: , и, более того, с помощью «ускорителя» легко узнать итоговое уравнение:

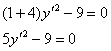
– две параллельные прямые. Ещё раз подчёркиваю, что полученное уравнение имеет место в новой системе координат , повёрнутой относительно исходной системы на угол , и, соответственно, прямые будут параллельны новой оси .

Полезно знать, что вырожденное уравнение параболического типа несложно выразить в явном виде и в исходной системе координат, поскольку проходят тривиальные алгебраические преобразования. Например:

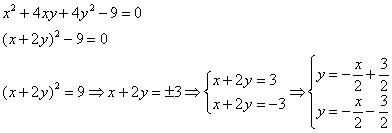
Полученный результат удобно использовать для самопроверки и выполнения чертежа.

Что касается инвариантов, то дела тут обстоят хуже. Если для параболы мы ещё смогли вытянуть некоторую информацию из инвариантов, то здесь будем созерцать малополезный набор .

Систематизируем порядок действий в параболическом случае::

1) Из формулы или находим угол поворота исходной системы координат :

2) Для данного угла «альфа» рассчитываем . При этом проводим максимальные упрощения: выносим из-под корней всё, что можно вынести, и избавляемся от многоэтажных дробей, если таковые образовались.

3) Подставляем найденные значения в формулы поворота .

4) Подставляем найденные выражения поворота в исходное уравнение , внимательно раскрываем все скобки и приводим подобные слагаемые, в результате чего в новой системе координат должно получиться уравнение вида , где .

4*) Примерно в 15% случаев (с нецентральной линией) может получиться уравнение, которое определяет параболу, развёрнутую относительно своего канонического положения (положительного направления оси ) на 180 градусов. Тогда следует вернуться к Пункту 2 алгоритма, рассмотреть противоположный угол поворота и использовать формулы , не забывая, что само значение тангенса осталось таким же: .

5) В полученном уравнении выделяем полный квадрат (если необходимо), в результате чего должно получиться уравнение вида , где – некоторые константы. И, наконец, после параллельного переноса системы координат началом в точку (замен и перехода к окончательной системе координат ) наша цель достигнута:

6) Чертёж. Повторюсь, что во многих случаях пойдёт и схематическая версия, поскольку рисовать линии 2-го порядка под градусом – занятие нелёгкое.

И в заключение коротко об общем алгоритме решения, который годится для всех случаев, и из которого, собственно, следуют все рассмотренные выше схемы:

1) По уравнению составляем характеристическое уравнение , где , – старые знакомые инварианты.

2) Решаем квадратное уравнение и находим его корни . При любых раскладах это будут действительные корни.

3) Данные корни определяют два угла поворота системы координат, вычисляем их тангенсы:

Теперь нам нужно выбрать нужный угол (тот, который приведёт к каноническому виду). Выбор осуществляем на черновике, методом «практического тыка». Опытные читатели могут провести анализ в уме или даже сразу «увидеть» желаемый вариант.

4) Начинаем с 1-го угла. Берём значение и рассчитываем косинус и синус этого угла: . Найденные значения подставляем в формулы поворота: .

5) Подставляем и в исходное уравнение и проводим упрощения. Если всё сделано правильно, то должно получиться уравнение вида:
в системе

Но это может оказаться неканоническое уравнение, и тогда пункты 4, 5 следует проделать для второго угла. Кроме того, в случае с параболой есть ещё одна заморочка с углами, которую я подробно осветил в Примере 3.

6) В уравнении выделяем полные квадраты: и с помощью замен (параллельного переноса системы в точку ) переходим к уравнению в системе . Образец сего действия неоднократно встречался ранее, в частности, в том же Примере 3.

7) Доводим уравнение до ума – чтобы получилось одно из девяти канонических уравнений.

Основная трудность общего способа состоит в его длительности и трудоёмкости, но любители сложностей могут потягать им Примеры № 1, 2. Ну а некоторые оказываются любителями поневоле :) – на первом курсе Физмата мне «повезло» с билетом по аналитической геометрии и я где-то 3 часа мучался с поворотом линии 2-го порядка, решая задачу в общем виде. Поэтому сейчас было бы просто кощунственно скрыть от вас эти знания!

Успехов!

Решения и ответы:

Пример 2. Решение: приведём данной линии к каноническому виду в новой системе координат .

Из уравнения находим коэффициенты:

Вычислим инварианты:

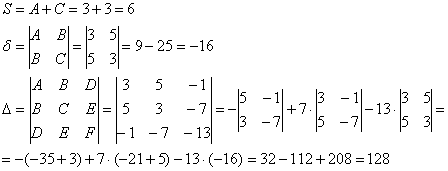
Примечание: последний определитель выгоднее раскрыть по 3-й строке либо 3-му столбцу.

Составим и решим систему:

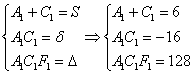
Из 1-го уравнения выражаем – подставляем во второе уравнение:

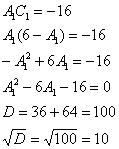
Таким образом, получаются две пары корней:

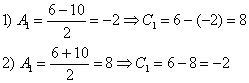
Примечание: решение несложно найти и подбором.

Подставим в третье уравнение системы:

Подставляем (сначала мысленно либо на черновике!) значения в уравнение :

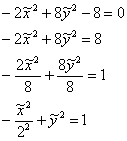
В результате получена неканоническая запись гиперболы (см. материалы параграфа о повороте гиперболы), т.е. первый набор корней нас не устраивает.

Подставляем второй комплект корней :

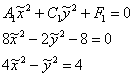
– гипербола с центром в точке , действительной полуосью , мнимой полуосью .

Примечание: опытный читатель сразу выберет 2-й комплект корней – из тех соображений, что у итогового уравнения коэффициент при должен оказаться положительным.

Координаты начала новой системы координат найдём из решения системы:

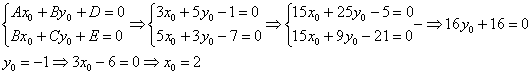
Таким образом:

Найдём угол поворота новой системы координат относительно старой.
Так как , то формула не даёт однозначного ответа об угле поворота. Поэтому используем формулу:

Выполним чертёж:

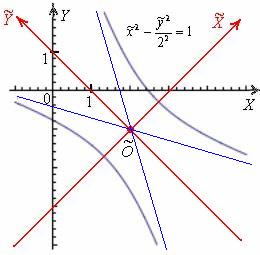
Ответ: – каноническая гипербола с полуосями в системе координат с началом в точке (координаты старой системы), повёрнутой относительно исходной системы координат на угол .

Дополнительная информация: гиперболический случай выражается аналитическим условием ( и имеют разные знаки). Если инвариант , то коэффициент , и гипербола вырождается в две пересекающиеся прямые (пункт № 5 классификации). В нашем примере гипотетически получилось бы уравнение: – двух пересекающихся прямых , которые, кстати, представляют собой асимптоты рассмотренной гиперболы (изображены синим цветом на чертеже).

Пример 4. Решение: сначала выяснить тип линии. Для этого вычислим определитель, составленный из коэффициентов :
, значит, данное уравнение задаёт нецентральную линию.

Осуществим поворот прямоугольной системы координат и переход к новой системе координат так, чтобы получить уравнение вида , где .

Найдём искомый угол поворота:

Если , то:

Подставим в формулы поворота:

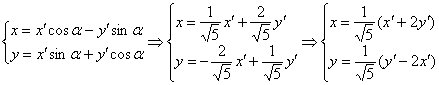
Подставим и в исходное уравнение :

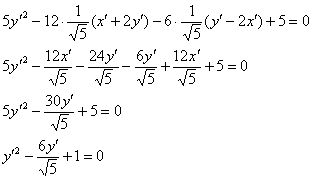
Выделим полный квадрат:

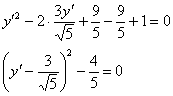
Осуществим параллельный перенос системы координат началом в точку . Проведём замену и запишем уравнение линии в новой системе координат :

– пара прямых , параллельных оси .
Выполним чертёж:

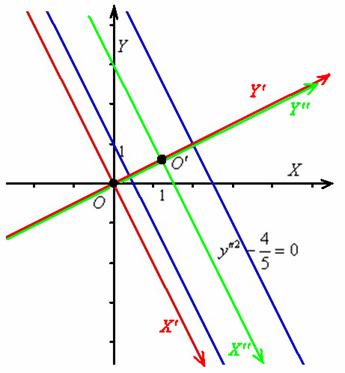
Ответ: данная линия представляет собой пару параллельных прямых, каноническое уравнение которых получается путём поворота системы координат вокруг своего начала на угол и её дальнейшим параллельным переносом в точку .