


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Свойства определителя. Понижение порядка определителя
На втором уроке мы узнаем основные свойства определителя, а также научимся приёмам их эффективного вычисления. Если вы слабо ориентируетесь в теме, пожалуйста, начните с одной из древнейших статей сайта – Как вычислить определитель? Она поможет не только чайникам, но даже тем, кто впервые услышал слово «определитель». Минуло два года с тех пор, когда на сайте было всего десять страничек, и вот, после моего долгого-долгого путешествия в мир матана, всё возвращается на круги своя.
Представьте, что вам нужно вычислить определитель третьего порядка, разложив его по элементам строки (столбца). Хотя чего тут представлять – нужно же =) Над ним можно сидеть 5 минут, а можно 2-3 минуты. Или даже в районе одной минуты. Время, которое вы потратите, зависит не только от вашего опыта, но и от знаний свойств определителей. Не редкость, когда процесс решения вполне реально сократить до считанных секунд, а иногда и сразу увидеть результат! «Ерунда, чего экономить на спичках, и так всё решим», – скажут некоторые. Допустим. И не допустим оплошностей ;-) Но как быть с достаточно распространённым на практике определителем 4-го порядка? Воевать с этим перцем придётся уже 10-20 минут. И это будет даже не бой, а бойня, поскольку очень велика вероятность вычислительной ошибки, которая «завернёт» вас на второй круг решения. А если определитель пятого порядка? Спасёт только понижение порядка определителя. Да, такие примеры тоже встречаются в контрольных работах.
Материалы данной страницы позволят значительно улучшить вашу технику решения определителей и упростят дальнейшее освоение высшей математики.
Эффективные методы вычисления определителя
В первую очередь коснёмся не свойств определителя, а как раз методов его рационального вычисления. Эти приёмы решения лежат на поверхности и понятны многим, но всё-таки остановимся на них подробнее. Предполагается, что читатель уже умеет достаточно уверенно раскрывать определитель третьего порядка. Как известно, данный определитель можно раскрыть 6 стандартными способами: по любой строке или любому столбцу. Казалось бы, без разницы, ведь ответ получится один и тот же. Но все ли способы одинаково легкИ? Нет. В большинстве случаев есть менее выгодные пути и более выгодные пути решения.
Рассмотрим определитель 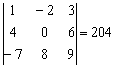 , который я обильно покрыл татуировками ещё на первом уроке. В той статье мы подробно, с картинками разложили его по первой строке. Первая строка – это хорошо и академично, однако нельзя ли быстрее достичь результата? В определителе есть ноль, и, раскрывая его по второй строке либо по второму столбцу, вычислений заметно поубавится!
, который я обильно покрыл татуировками ещё на первом уроке. В той статье мы подробно, с картинками разложили его по первой строке. Первая строка – это хорошо и академично, однако нельзя ли быстрее достичь результата? В определителе есть ноль, и, раскрывая его по второй строке либо по второму столбцу, вычислений заметно поубавится!
Разложим определитель по второму столбцу:
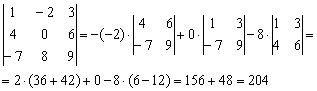
На практике нулевые элементы игнорируются, и запись решения принимает более компактный вид:
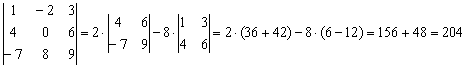
Задание 1
Раскройте данный определитель по второй строке, используя укороченную запись.
Решение в конце урока.
Если в строке (либо столбце) два нуля, то это вообще настоящий подарок. Рассмотрим определитель 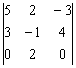 . Здесь два нуля в третьей строке, по ней и раскрываем:
. Здесь два нуля в третьей строке, по ней и раскрываем:
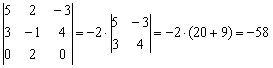
Вот и всё решение!
Особый случай, когда определитель имеет так называемый ступенчатый или треугольный вид, например:  – в таком определителе все числа, расположенные ниже главной диагонали, равны нулю.
– в таком определителе все числа, расположенные ниже главной диагонали, равны нулю.
Разложим его по первому столбцу:
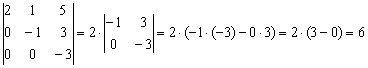
В практических заданиях удобно руководствоваться следующим правилом – ступенчатый определитель равен произведению чисел его главной диагонали:
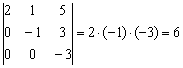
Аналогичный принцип справедлив и для ступенчатых определителей других порядков, например:
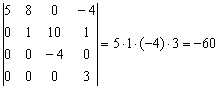
Треугольные определители появляются в некоторых задачах линейной алгебры, и их решение чаще всего оформляют именно так.
А если в строке (столбце) определителя находятся одни нули? Ответ, думаю, понятен. Мы ещё вернёмся к этому вопросу в свойствах определителя.
Теперь представим, что долгожданные баранки не положены в новогодний подарок. Так давайте же распотрошим нехорошего Санта-Клауса!
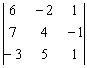
Здесь нет нулей, но всё равно существует способ облегчить себе жизнь. Данный определитель оптимальнее разложить по третьему столбцу, поскольку там самые маленькие числа. При этом запись решения принимает весьма лаконичный вид:
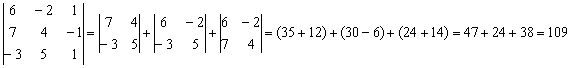
Резюмируя параграф, сформулируем золотое правило вычислений:
Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где:
1) нулей побольше;
2) числа поменьше.
Естественно, это справедливо и для определителей высших порядков.
Небольшой пример для закрепления материала:
Задание 2
Вычислить определитель, раскрыв его по строке либо столбцу, используя при этом наиболее рациональный способ
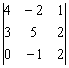
Это пример для самостоятельного решения, оптимальное решение и ответ – в конце урока.
И ещё один важный совет: не комплексуйте! Не нужно «зацикливаться» на традиционном разложении по первой строке либо первому столбцу. Как короче – так и решайте!
Свойства определителя
Насчитывается порядка десяти свойств определителя (смотрите учебники, справочники), однако реальное прикладное значение имеют только некоторые из них. И сейчас я попытаюсь в подробной и доступной форме поделиться практическим опытом использования данных свойств.
Рассмотрим старых знакомых первого урока: матрицу 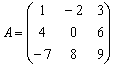 и её определитель
и её определитель 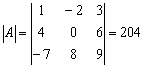 .
.
На всякий случай повторю элементарное различие между понятиями: матрица – это таблица элементов, а определитель – это число.
При транспонировании матрицы величина её определителя не меняется
Транспонируем матрицу:
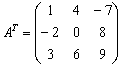
Примечание: действие подробно разобрано на уроке Действия с матрицами.
Согласно свойству, определитель транспонированной матрицы равен тому же значению: 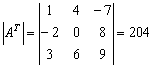 . Желающие могут убедиться в этом самостоятельно.
. Желающие могут убедиться в этом самостоятельно.
В ходу и более простецкая формулировка данного свойства: если транспонировать определитель, то его величина не изменится.
Запишем оба определителя рядышком и проанализируем один важный момент:
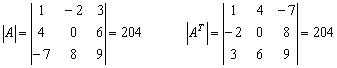
В результате транспонирования первая строка стала первым столбцом, вторая строка – вторым столбцом, третья строка – третьим столбцом. Строки стали столбцами, а результат не изменился. Из чего следует важный факт: строки и столбцы определителя равноправны. Иными словами, если какое-нибудь свойство справедливо для строки, то аналогичное свойство справедливо и для столбца! В действительности с этим мы уже давно столкнулись – ведь определитель можно раскрыть как по строке, так равноправно и по столбцу.
Не нравятся числа в строках? Транспонируйте определитель! Возникает только один вопрос, зачем? Практический смысл рассмотренного свойства невелик, но его полезно закинуть в багаж знаний, чтобы лучше понимать другие задачи высшей математики. Например, сразу становится ясно, почему при исследовании векторов на компланарность их координаты можно записать как в строки определителя, так и в столбцы.
Если две строки (или два столбца) определителя поменять местами,
то определитель сменит знак
! Помните, речь идёт об определителе! В самой матрице переставлять ничего нельзя!
Сыграем в кубик-рубик с определителем 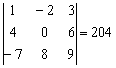 .
.
Поменяем первую и третью строку местами:
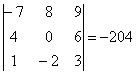
Определитель сменил знак.
Теперь в полученном определителе переставим вторую и третью строки:
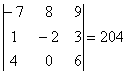
Определитель ещё раз изменил знак.
Переставим второй и третий столбец:
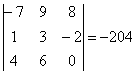
То есть, любая парная перестановка строк (столбцов) влечёт изменение знака определителя на противоположный.
Игры играми, но на практике такие действия лучше не использовать. Толку от них особого нет, а вот запутаться и допустить ошибку несложно. Однако приведу одну из немногих ситуаций, когда в этом действительно есть смысл. Предположим, что в ходе решения некоторого примера у вас нарисовался определитель со знаком «минус»:
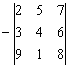
Раскроем его, скажем, по первой строке:
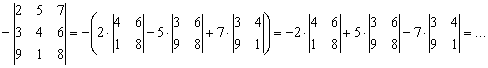
Очевидное неудобство состоит в том, что пришлось выполнять лишние реверансы – ставить большие скобки, а затем их раскрывать (кстати, крайне не рекомендую выполнять подобные действия «за один присест» устно).
Чтобы избавиться от «минуса», рациональнее поменять местами любые две строки или любые два столбца. Переставим, например, первую и вторую строки:
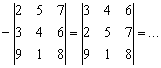
Теперь впереди помех нет, можно ехать дальше. Заядлых гонщиков ждёт кирпич: 29.
Выглядит стильно, но в большинстве случаев с отрицательным знаком целесообразнее разбираться другим способом (читайте дальше).
Рассмотренное действие опять же помогает лучше понять, например, некоторые свойства векторного произведения векторов или смешанного произведения векторов.
А вот это уже более интересно:
Из строки (столбца) определителя можно вынести общий множитель
!!! Внимание! В правиле речь идёт об ОДНОЙ строке или об ОДНОМ столбце определителя. Пожалуйста, не путайте с матрицами, в матрице множитель выносится/вносится у ВСЕХ чисел сразу.
Начнём с частного случая правила – вынесения «минус единицы» или просто «минуса».
Встречаем очередного пациента: 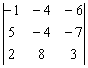 .
.
В данном определителе слишком много минусов и неплохо бы сократить их количество.
Вынесем –1 из первой строки:
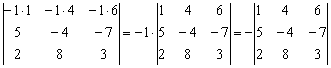
Или короче:
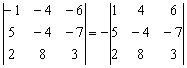
Минус перед определителем, как уже демонстрировалось – не есть удобно. Смотрим на вторую строку определителя и замечаем, что минусов там тоже многовато.
Вынесем «минус» из второй строки:
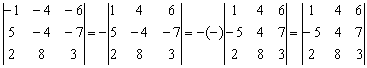
Что можно сделать ещё? Все числа второго столбца делятся на 4 без остатка. Вынесем 4 из второго столбца:
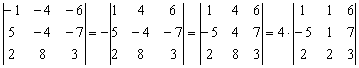
Справедливо и обратное правило – множитель можно не только вынести, но и внести, причём, в ЛЮБУЮ строку или в ЛЮБОЙ столбец определителя.
Ради шутки умножим на 4 третью строку определителя:
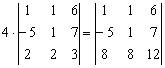
Дотошные умы могут убедиться в равенстве исходного 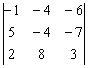 и полученного
и полученного 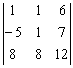 определителей (верный ответ: –216).
определителей (верный ответ: –216).
На практике часто выполняют внесение минуса. Рассмотрим определитель 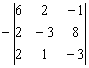 . Отрицательный знак перед определителем можно внести в ЛЮБУЮ строку или в ЛЮБОЙ столбец. Самым лучшим кандидатом является третий столбец, в него и внесём минус:
. Отрицательный знак перед определителем можно внести в ЛЮБУЮ строку или в ЛЮБОЙ столбец. Самым лучшим кандидатом является третий столбец, в него и внесём минус:
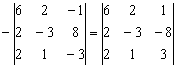
Также замечаем, что все числа первого столбца делятся на 2 без остатка, но стОит ли выносить «двойку»? Если вы собираетесь понижать порядок определителя (о чём пойдет речь в заключительном разделе), то, безусловно, стОит. Но если раскрывать определитель по строке (столбцу), то «двойка» впереди только удлинит запись решения.
Однако если множитель велик, например, 13, 17 и т.п., то его, конечно, по-любому выгоднее вынести. Познакомимся с маленьким монстром: ![]() . Из первой строки вынесем –11, из второй строки вынесем –7:
. Из первой строки вынесем –11, из второй строки вынесем –7:
![]()
Вы скажете, вычисления и так быстро щёлкаются на обычном калькуляторе? Это правда. Но, во-первых, его может не оказаться под рукой, а во-вторых, если дан определитель 3-го или 4-го порядка с большими числами, то и стучать по кнопкам уже не сильно захочется.
Задание 3
Вычислить определитель с помощью вынесения множителей из строк и столбцов 
Это пример для самостоятельного решения.
Ещё пара полезных правил:
Если две строки (столбца) определителя пропорциональны
(как частный случай – одинаковы), то данный определитель равен нулю
Здесь пропорциональны соответствующие элементы первой и второй строки:
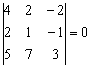
Иногда говорят, что строки определителя линейно зависимы. Так как при транспонировании величина определителя не меняется, то из линейной зависимости строк следует и линейная зависимость столбцов.
В пример можно вложить геометрический смысл – если считать, что в строках записаны координаты векторов пространства, то первые два вектора с пропорциональными координатами будут коллинеарны, а значит, все три вектора – линейно зависимы, то есть компланарны.
В следующем примере пропорциональны три столбца (и, к слову, три строки тоже):
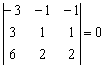
Здесь второй и третий столбец одинаковы, это частный случай – когда коэффициент пропорциональности равен единице
Перечисленные свойства вполне можно использовать на практике. Но помните, повышенный уровень знаний иногда наказуем ;-) Поэтому, возможно, лучше раскрывать такие определители обычным способом (зная наперёд, что получится ноль).
Следует отметить, что обратное в общем случае неверно – если определитель равен нулю, то из этого ещё не следует, что его строки (столбцы) пропорциональны. То есть линейная зависимость строк/столбцов может быть и не явной.
Существуют и более очевидный признак, когда сразу можно сказать, что определитель нулевой:
Определитель с нулевой строкой (столбцом) равен нулю
Пример: 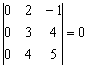
«Любительская» проверка элементарна, раскроем определитель по первому столбцу:
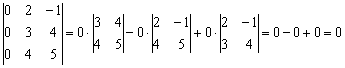
Впрочем, результат не изменится, если раскрыть определитель по любой строке или любому столбцу.
Выжимаем второй стакан апельсинового сока:
Какие свойства определителей полезно знать?
1) Величина определителя не меняется при транспонировании. Свойство запоминаем.
2) Любая парная перестановка строк (столбцов) меняет знак определителя на противоположный. Свойство тоже запоминаем и стараемся не использовать во избежание путаницы.
3) Из строки (столбца) определителя можно вынести множитель (и внести его обратно). Используем там, где это выгодно.
4) Если строки (столбцы) определителя пропорциональны, то он равен нулю. Определитель с нулевой строкой (столбцом) равен нулю.
На протяжении урока неоднократно наблюдалась элементарная закономерность – чем больше в строке (столбце) нулей, тем легче вычислить определитель. Возникает вопрос, а нельзя ли нули организовать специально с помощью какого-нибудь преобразования? Можно! Познакомимся ещё с одним очень мощным свойством:
Понижение порядка определителя
Очень хорошо, если вы уже разобрались с методом Гаусса и имеете опыт решения систем линейных уравнений этим способом. Фактически сформулированное ниже свойство дублирует одно из элементарных преобразований.
Чтобы нагулять аппетит раздавим маленького лягушонка:
![]()
К строке определителя можно прибавить другую строку, умноженную на ненулевое число. При этом величина определителя не изменится
Пример: в определителе ![]() получим ноль слева вверху.
получим ноль слева вверху.
Для этого вторую строку мысленно либо на черновике умножим на 3: (–3, 6) и к первой строке прибавим вторую строку, умноженную на 3:
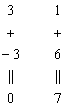
Результат записываем в первую строку:
![]()
Проверка: ![]()
Теперь в том же определителе ![]() получим ноль справа внизу. Для этого ко второй строке прибавим первую строку, умноженную (мысленно) на –2 (смотрим и считаем снизу вверх):
получим ноль справа внизу. Для этого ко второй строке прибавим первую строку, умноженную (мысленно) на –2 (смотрим и считаем снизу вверх):
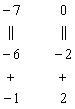
Результат записываем во вторую строку:
![]()
Обратите внимание: при элементарном преобразовании меняется ТА строка, к которой прибавляЮТ.
Сформулируем зеркальное правило для столбцов:
К столбцу определителя можно прибавить другой столбец, умноженный на ненулевое число. При этом величина определителя не изменится
Возьмём за лапки животное ![]() и, используя данное преобразование, получим ноль слева вверху. Для этого мысленно либо на черновике умножим второй столбец на –3:
и, используя данное преобразование, получим ноль слева вверху. Для этого мысленно либо на черновике умножим второй столбец на –3: ![]() и к первому столбцу прибавим второй столбец, умноженный на –3:
и к первому столбцу прибавим второй столбец, умноженный на –3:
![]()
Результат запишем в первый столбец:
![]()
И, наконец, в определителе ![]() получим ноль справа внизу. Для этого ко второму столбцу прибавим первый столбец, умноженный (мысленно) на 2 (смотрим и считаем справа налево):
получим ноль справа внизу. Для этого ко второму столбцу прибавим первый столбец, умноженный (мысленно) на 2 (смотрим и считаем справа налево):
![]()
Результат помещаем во второй столбец:
![]()
При элементарном преобразовании меняется ТОТ столбец, к которому прибавляЮТ.
Постарайтесь качественно переварить нижеследующий пример.
Отправим в суп подросшее земноводное:
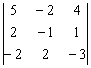
Задача состоит в том, чтобы с помощью элементарных преобразований понизить порядок определителя до второго порядка.
С чего начать? Сначала в определителе нужно выбрать число-«мишень». В качестве «мишени» почти всегда выступает единица либо –1. Смотрим на определитель и замечаем, что здесь даже выбор есть. Пусть числом-«мишенью» будет элемент ![]() :
:
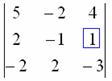
Примечание: смысл двойных подстрочных индексов можно узнать в статье Правило Крамера. Матричный метод. В данном случае индексы элемента ![]() говорят нам о том, что он располагается во второй строке, третьем столбце.
говорят нам о том, что он располагается во второй строке, третьем столбце.
Идея состоит в том, чтобы получить два нуля в третьем столбце:
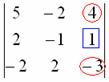
Либо получить два нуля во второй строке:
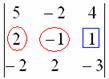
Во второй строке числа поменьше (не забываем золотое правило), поэтому выгоднее взять именно её. А третий столбец с числом-«мишенью» останется неизменным:
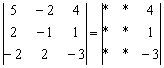
Ко второму столбцу прибавляем третий столбец:
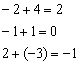
Тут и умножать ничего не пришлось.
Результат записываем во второй столбец:
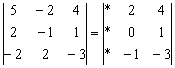
К первому столбцу прибавляем третий столбец, умноженный (мысленно) на –2:
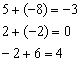
Результат записываем в первый столбец, раскладываем определитель по второй строке:
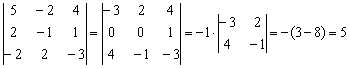
Как мы понизили порядок определителя? Получили два нуля во второй строке.
Решим пример вторым способом, организуем нули в третьем столбце:
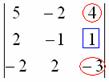
Вторая строка с числом-«мишенью» останется неизменной:
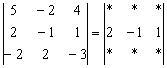
К первой строке прибавим вторую строку, умноженную (мысленно) на –4:
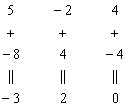
Результат записываем в первую строку:
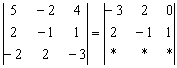
К третьей строке прибавим вторую строку, умноженную (мысленно) на 3 (смотрим и считаем снизу вверх):
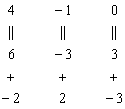
Результат записываем в третью строку, определитель раскрываем по третьему столбцу:
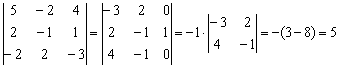
Заметьте, что нет никакой необходимости переставлять строки или столбцы. Элементарные преобразования прекрасно работают как слева направо, так и справа налево. Как сверху вниз, так и снизу вверх.
Задание 4
Вычислить тот же определитель 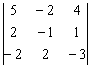 , выбрав в качестве числа-«мишени» элемент
, выбрав в качестве числа-«мишени» элемент ![]() . Понизить его порядок двумя способами: получив нули во второй строке и получив нули во втором столбце.
. Понизить его порядок двумя способами: получив нули во второй строке и получив нули во втором столбце.
Это пример для самостоятельного решения. Полное решение и краткие комментарии в конце урока.
Иногда в определителе отсутствует единица либо –1, например: 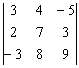 . В этом случае «мишень» следует организовать с помощью дополнительного элементарного преобразования. Сделать это можно чаще всего несколькими способами. Например: к первой строке прибавим вторую строку, умноженную –1:
. В этом случае «мишень» следует организовать с помощью дополнительного элементарного преобразования. Сделать это можно чаще всего несколькими способами. Например: к первой строке прибавим вторую строку, умноженную –1:
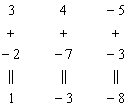
Результат записываем в первую строку:
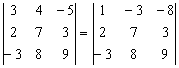
! Внимание: НЕ НУЖНО из первой строки вычитать вторую строку, это значительно увеличивает вероятность ошибки. Только складываем! Поэтому к первой строке прибавляем вторую строку, умноженную –1. Именно так!
Единица получена, чего и требовалось достичь. Далее можно получить два нуля в первой строке либо в первом столбце. Желающие могут довести решение до конца (верный ответ: –176).
Стоит отметить, что готовая «мишень» чаще всего присутствует в исходном определителе, а уж для определителя 4-го порядка и выше дополнительное преобразование крайне маловероятно.
Порубим на гуляш несколько крупных жаб:
Задача
Решить систему линейных уравнений по формулам Крамера
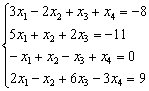
Ничего страшного, если вы ещё не успели ознакомиться с методом Крамера, в этом случае можно просто посмотреть, как понижается порядок у определителя «четыре на четыре». Да и само правило станет понятно, если чуть-чуть вникнуть в ход решения.
Решение: сначала вычислим главный определитель системы:

Есть возможность пойти стандартным путём, разложив данный определитель по строке либо столбцу. Вспоминая алгоритм первого урока, и, используя придуманную мной матрицу знаков 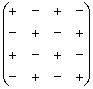 , раскроем определитель, например, по «классической» первой строке:
, раскроем определитель, например, по «классической» первой строке:
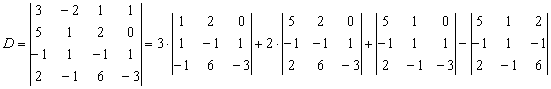
Не вижу вашего энтузиазма =) Безусловно, можно посидеть минут десять и аккуратно-внимательно родить правильный ответ. Но беда в том, что в дальнейшем предстоит вычислить ещё 4 определителя четвёртого порядка. Поэтому единственный разумный выход – понизить порядок определителя.
Единиц в определителе много, и наша задача выбрать лучший вариант. Вспоминаем золотое правило: в строке (столбце) нулей должно быть побольше, и числа – поменьше. По этой причине вполне подходит вторая строка либо четвёртый столбец. Четвёртый столбец выглядит привлекательнее, причём, там есть две единицы. В качестве «мишени» выбираем элемент ![]() :
:

Первая строка не изменится. И вторая тоже – там уже необходимый ноль:
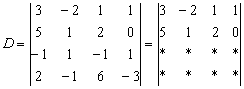
К третьей строке прибавим первую строку, умноженную на –1 (смотрим и считаем снизу вверх):
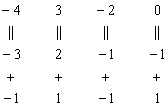
! Внимание ещё раз: Не нужно из третьей строки вычитать первую строку. Только складываем!
Результат записываем в третью строку:
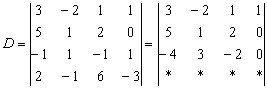
К четвёртой строке прибавим первую строку, умноженную на 3 (смотрим и считаем снизу вверх):
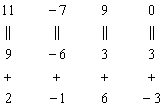
Результат записываем в четвёртую строку:
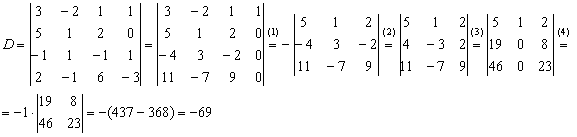
(1) Раскрываем определитель по четвёртому столбцу. Не забываем, что к элементу ![]() нужно добавить «минус» (см. матрицу знаков).
нужно добавить «минус» (см. матрицу знаков).
(2) Порядок определителя понижен до 3-го. В принципе, его можно разложить по строке (столбцу), но лучше отработаем свойства определителя. Вносим минус во вторую строку.
(3) Ко второй строке прибавим первую строку, умноженную на 3. К третьей строке прибавим первую строку, умноженную на 7.
(4) Раскрываем определитель по второму столбцу, тем самым ещё понижая его порядок до двух.
Заметьте, как сократилось решение! Главное, немного «набить руку» на элементарных преобразованиях, и такая возможность представится прямо сейчас. К тому же в вашем распоряжении есть калькулятор, который считает определители (в частности, его можно найти на странице Математические формулы и таблицы). С помощью калькулятора легко контролировать выполняемые действия. Получили определитель  на первом шаге – и сразу проверили, равен ли он исходному определителю.
на первом шаге – и сразу проверили, равен ли он исходному определителю.
Итак, ![]() , значит, система имеет единственное решение.
, значит, система имеет единственное решение.
Вычислим определитель  .
.
Появился ещё один ноль и очень вкусно выглядит третья строка. При этом в качестве «мишени» выгоднее выбрать элемент ![]() , получив нули в третьей строке:
, получив нули в третьей строке:
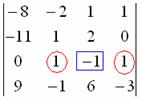
Тут даже умножать ничего не надо:
Ко второму столбцу прибавим третий столбец: 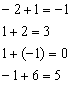 .
.
И к 4-му столбцу прибавим третий столбец: 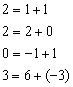 (смотрим и считаем справа налево)
(смотрим и считаем справа налево)
Решаем дальше:
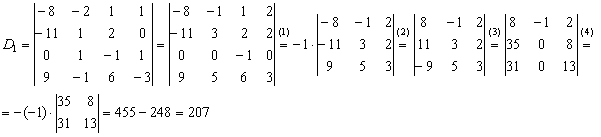
(1) Раскрываем определитель по третьей строке. Порядок определителя понижен до трёх.
(2) Вносим «минус» в первый столбец.
(3) Ко второй строке прибавим первую строку, умноженную на 3. К третьей строке прибавим первую строку, умноженную на 5.
(4) Раскрываем определитель по второму столбцу, понижая порядок определителя до двух.
По формулам Крамера:
![]()
Вычислим определитель  .
.
Так получается, что в рассматриваемых определителях у нас есть нули, в произвольной же задаче их может и не быть. Поэтому для разнообразия оставим нули в покое и раскроем определитель не очень выгодным способом. Выберем элемент ![]() и получим нули в первой строке:
и получим нули в первой строке:

Поехали:
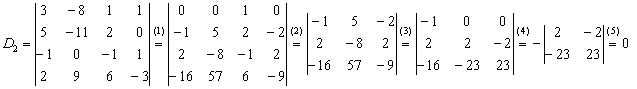
(1) К первому столбцу прибавим третий столбец, умноженный на –3. Ко второму столбцу прибавим третий столбец, умноженный на 8. К четвёртому столбцу прибавим третий столбец, умноженный на –1.
(2) Раскрываем определитель по первой строке. Порядок определителя понижен до трёх.
(3) Ко второму столбцу прибавим первый столбец, умноженный на 5. К третьему столбцу прибавим первый столбец, умноженный на –2.
(4) Раскрываем определитель по первой строке. Порядок определителя понижен до двух.
(5) Столбцы определителя пропорциональны, значит, он равен нулю.
По формулам Крамера:
![]()
Задание 5
Самостоятельно вычислить определители 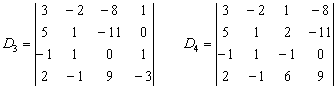
и найти ![]()
Концовка решения и ответ на дне страницы. Ваш путь решения может отличаться от моего пути решения, важно, чтобы совпали ответы.
Выбор строки или столбца для преобразований нередко обусловлен не только числами, но и удобством решения с субъективной точки зрения. Кому-то удобнее решать по строкам, а кому-то по столбцам. У чайников особенно популярен выбор «мишени» в первой строке, поскольку процесс будет напоминать метод Гаусса.
Замечательный получается у нас комплексный обед, и пришло время десерта:

Это уже даже не жаба, это сам Годзилла. Возьмём заготовленный стакан апельсинового сока и посмотрим, как понижается порядок определителя. Алгоритм, думаю, понятен: с пятого порядка понижаем до четвёртого, с четвёртого – до третьего и с третьего – до второго:
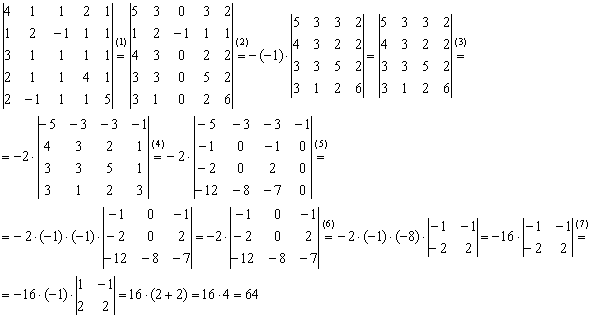
(1) К первой, третьей, четвертой и пятой строкам прибавим вторую строку.
(2) Раскрываем определитель по 3-му столбцу. Порядок определителя понизился до четырёх.
(3) Из 4-го столбца выносим 2. Первую строку умножаем на –1, и чтобы определитель не изменился, ставим перед ним «минус». Данное преобразование выполнено в целях упростить дальнейшие вычисления.
(4) Ко второй и третьей строкам прибавим первую строку. К четвертой строке прибавим первую строку, умноженную на 3.
(5) Раскрываем определитель по 4-му столбцу. Порядок понижен до трёх.
(6) Раскрываем определитель по 2-му столбцу. Порядок понижен до двух.
(7) Выносим «минус» из 1-го столбца.
Всё вышло проще, чем казалось, у всех монстров есть слабые места!
Неутомимые читатели могут попробовать решить определитель пятого порядка каким-нибудь другим способом, благо, единиц в нём тьма.
Заходите, завтра в меню крокодилы!
Решения и ответы:
Задание 1: Решение:
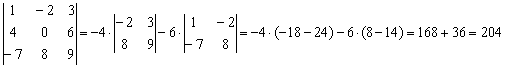
Задание 2: Решение: определитель выгоднее вычислить по третьей строке:
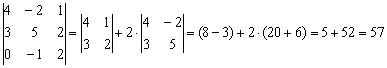
Разложение по первому столбцу менее рационально – там числа больше, и вычисления чуть более громоздкие.
Задание 3: Решение:
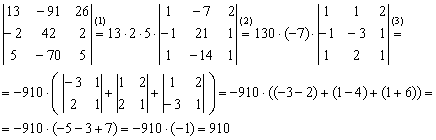
(1) Из первой строки вынесли 13, из второй строки вынесли 2, из третьей строки вынесли 5.
(2) Из второго столбца вынесли –7.
(3) Разложили определитель по первому столбцу.
Задание 4: Решение: Понизим порядок определителя, получив нули во второй строке:
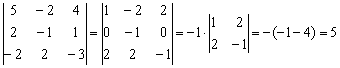
К первому столбцу прибавили второй столбец, умноженный на 2. К третьему столбцу прибавили второй столбец. Определитель раскрыли по второй строке.
Понизим порядок определителя, получив нули во втором столбце:
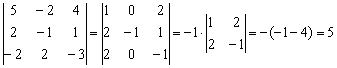
К первой строке прибавили вторую строку, умноженную на –2. К третьей строке прибавили вторую строку, умноженную на 2. Определитель раскрыли по второму столбцу.
Задание 5: Решение:
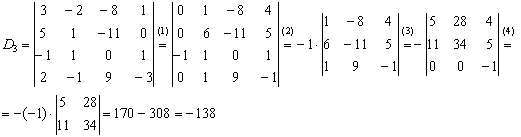
(1) К первой строке прибавим третью строку, умноженную на 3. Ко второй строке прибавим третью строку, умноженную на 5. К 4-й строке прибавим третью строку, умноженную на 2.
(2) Раскрываем определитель по первому столбцу.
(3) Ко второму столбцу прибавим третий столбец, умноженный на 9. К первому столбцу прибавим третий столбец.
(4) Раскрываем определитель по третьей строке.
![]()
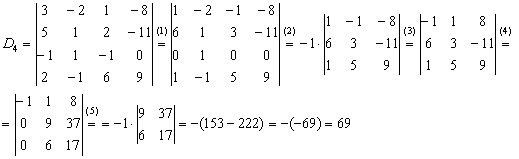
(1) К первому столбцу прибавим второй столбец. К третьему столбцу прибавим второй столбец
(2) Раскрываем определитель по третьей строке.
(3) Вносим «минус» в первую строку.
(4) Ко второй строке прибавим первую строку, умноженную на 6. К третьей строке прибавим первую строку
(5) Раскрываем определитель по первому столбцу.
![]()
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright