


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Уравнение прямой на плоскости.
Направляющий вектор прямой. Вектор нормали
Прямая линия на плоскости – это одна из простейших геометрических фигур, знакомая вам ещё с младших классов, и сегодня мы научимся обращаться с ней методами аналитической геометрии. Поэтому, уважаемые чайники, сначала разогрейте тему векторов, иначе понимание материала будет неполным. О прямой я уже вкратце напомнил в статье о графиках функций, и сейчас всё будет по-серьёзному… или не очень :)
Для подготовленных читателей горячие ссылки:
- Уравнение прямой с угловым коэффициентом
- Как составить уравнение прямой с угловым коэффициентом?
- Общее уравнение прямой
- Направляющий вектор прямой
- Как составить уравнение прямой по точке и направляющему вектору?
- Как найти направляющий вектор по общему уравнению прямой?
- Как составить уравнение прямой по двум точкам?
- Вектор нормали прямой
- Как составить уравнение прямой по точке и вектору нормали?
- Уравнение прямой в отрезках
- Параметрические уравнения прямой
- Простейшие задачи с прямой
и мы начинаем.
Уравнение прямой с угловым коэффициентом
Всем известный «школьный» вид уравнения прямой ![]() называется уравнением прямой с угловым коэффициентом
называется уравнением прямой с угловым коэффициентом ![]() . Например, если прямая задана уравнением
. Например, если прямая задана уравнением ![]() , то её угловой коэффициент:
, то её угловой коэффициент: ![]() . Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:
. Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:
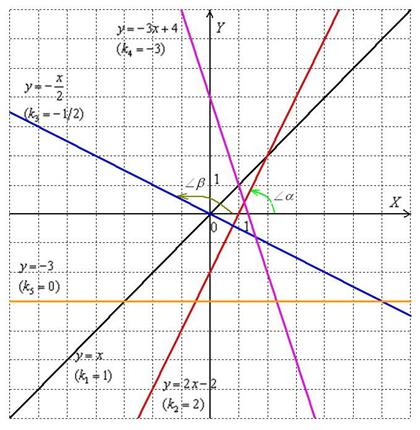
Нетрудно показать, что угловой коэффициент прямой равен тангенсу угла между положительным направлением оси ![]() и данной прямой:
и данной прямой: ![]() , причём угол
, причём угол ![]() «откручивается» против часовой стрелки.
«откручивается» против часовой стрелки.
Чтобы не загромождать чертёж, я нарисовал углы только для двух прямых. Рассмотрим «красную» прямую ![]() и её угловой коэффициент
и её угловой коэффициент ![]() . Согласно вышесказанному:
. Согласно вышесказанному: ![]() (угол «альфа» обозначен зелёной дугой). Для «синей» прямой
(угол «альфа» обозначен зелёной дугой). Для «синей» прямой ![]() с угловым коэффициентом
с угловым коэффициентом ![]() справедливо равенство
справедливо равенство ![]() (угол «бета» обозначен болотной дугой). А если известен тангенс угла, то легко найти и сам угол с помощью обратной функции – арктангенса, тригонометрическая таблица или калькулятор в руки. Монстры даже помнят некоторые значения :)
(угол «бета» обозначен болотной дугой). А если известен тангенс угла, то легко найти и сам угол с помощью обратной функции – арктангенса, тригонометрическая таблица или калькулятор в руки. Монстры даже помнят некоторые значения :)
Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс. При этом возможны следующие случаи:
1) Если угловой коэффициент отрицателен: ![]() , то линия, грубо говоря, идёт сверху вниз. Примеры – синяя и малиновая прямые на чертеже.
, то линия, грубо говоря, идёт сверху вниз. Примеры – синяя и малиновая прямые на чертеже.
2) Если угловой коэффициент положителен: ![]() , то линия идёт снизу вверх. Примеры – чёрная и красная прямые на чертеже.
, то линия идёт снизу вверх. Примеры – чёрная и красная прямые на чертеже.
3) Если угловой коэффициент равен нулю: ![]() , то уравнение
, то уравнение ![]() принимает вид
принимает вид ![]() , и соответствующая прямая параллельна оси
, и соответствующая прямая параллельна оси ![]() . Пример – жёлтая прямая.
. Пример – жёлтая прямая.
4) Для семейства прямых ![]() , параллельных оси
, параллельных оси ![]() (на чертеже нет примера, кроме самой оси
(на чертеже нет примера, кроме самой оси ![]() ), углового коэффициента не существует (тангенс 90 градусов не определён).
), углового коэффициента не существует (тангенс 90 градусов не определён).
Чем больше угловой коэффициент по модулю, тем круче идёт график прямой.
Например, рассмотрим две прямые ![]() . Здесь
. Здесь ![]() , поэтому прямая
, поэтому прямая ![]() имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.
имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.
В свою очередь, прямая ![]() более крутА, чем прямые
более крутА, чем прямые ![]() .
.
Обратно: чем меньше угловой коэффициент по модулю, тем прямая является более пологой.
Для прямых ![]() справедливо неравенство
справедливо неравенство ![]() , таким образом, прямая
, таким образом, прямая ![]() более полога. Детская горка, чтобы не насадить себе синяков и шишек.
более полога. Детская горка, чтобы не насадить себе синяков и шишек.
Зачем это нужно?
Продлить ваши мучения Знания вышеперечисленных фактов позволяет немедленно увидеть свои ошибки, в частности, ошибки при построении графиков – если на чертеже получилось «явно что-то не то». Желательно, чтобы вам сразу было понятно, что, например, прямая ![]() весьма крутА и идёт снизу вверх, а прямая
весьма крутА и идёт снизу вверх, а прямая ![]() – очень полога, близко прижата к оси
– очень полога, близко прижата к оси ![]() и идёт сверху вниз.
и идёт сверху вниз.
В геометрических задачах часто фигурируют несколько прямых, и поэтому их, вестимо, принято обозначать, а-таки не раскрашивать.
Обозначения: прямые обозначаются маленькими латинскими буквами: ![]() . Популярный вариант – обозначение одной и той же буквой с натуральными подстрочными индексами. Например, те пять прямых, которые мы только что рассмотрели, можно обозначить через
. Популярный вариант – обозначение одной и той же буквой с натуральными подстрочными индексами. Например, те пять прямых, которые мы только что рассмотрели, можно обозначить через ![]() .
.
Поскольку любая прямая однозначно определяется двумя точками, то её можно обозначать данными точками: ![]() и т. д. Обозначение
и т. д. Обозначение ![]() совершенно очевидно подразумевает, что точки
совершенно очевидно подразумевает, что точки ![]() принадлежат прямой
принадлежат прямой ![]() .
.
Пора немного размяться.
Как составить уравнение прямой с угловым коэффициентом?
Если известна точка ![]() , принадлежащая некоторой прямой, и угловой коэффициент
, принадлежащая некоторой прямой, и угловой коэффициент ![]() этой прямой, то уравнение данной прямой выражается формулой:
этой прямой, то уравнение данной прямой выражается формулой:
![]()
Пример 1
Составить уравнение прямой с угловым коэффициентом ![]() , если известно, что точка
, если известно, что точка ![]() принадлежит данной прямой.
принадлежит данной прямой.
Решение: уравнение прямой составим по формуле ![]() . В данном случае:
. В данном случае:
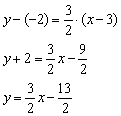
Ответ: ![]()
Проверка выполняется элементарно. Во-первых, смотрим на полученное уравнение ![]() и убеждаемся, что наш угловой коэффициент
и убеждаемся, что наш угловой коэффициент ![]() на своём месте. Во-вторых, координаты точки
на своём месте. Во-вторых, координаты точки ![]() должны удовлетворять данному уравнению. Подставим их в уравнение:
должны удовлетворять данному уравнению. Подставим их в уравнение:
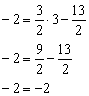
Получено верное равенство, значит, точка ![]() удовлетворяет полученному уравнению.
удовлетворяет полученному уравнению.
Вывод: уравнение найдено правильно.
Более хитрый пример для самостоятельного решения:
Пример 2
Составить уравнение прямой, если известно, что её угол наклона к положительному направлению оси ![]() составляет
составляет ![]() , и точка
, и точка ![]() принадлежит данной прямой.
принадлежит данной прямой.
Если возникли затруднения, перечитайте теоретический материал. Точнее больше практический, многие доказательства я пропускаю.
Прозвенел последний звонок, отгремел выпускной бал, и за воротами родной школы нас поджидает, собственно, аналитическая геометрия. Шутки закончились…. А может быть только начинаются =)
Общее уравнение прямой
Ностальгически машем ручкой привычному ![]() и знакомимся с общим уравнением прямой. Поскольку в аналитической геометрии в ходу именно оно.
и знакомимся с общим уравнением прямой. Поскольку в аналитической геометрии в ходу именно оно.
Общее уравнение прямой имеет вид: ![]() , где
, где ![]() – некоторые числа. При этом коэффициенты
– некоторые числа. При этом коэффициенты ![]() одновременно не равны нулю, так как уравнение теряет смысл.
одновременно не равны нулю, так как уравнение теряет смысл.
Оденем в костюм и галстук уравнение с угловым коэффициентом ![]() . Сначала перенесём все слагаемые в левую часть:
. Сначала перенесём все слагаемые в левую часть:
![]()
Слагаемое с «иксом» нужно поставить на первое место:
![]()
В принципе, уравнение уже имеет вид ![]() , но по правилам математического этикета коэффициент первого слагаемого (в данном случае
, но по правилам математического этикета коэффициент первого слагаемого (в данном случае ![]() ) должен быть положительным. Меняем знаки:
) должен быть положительным. Меняем знаки:
![]()
Готово.
Запомните эту техническую особенность! Первый коэффициент (чаще всего ![]() ) делаем положительным!
) делаем положительным!
В аналитической геометрии уравнение прямой почти всегда будет задано в общей форме. Ну а при необходимости его легко привести к «школьному» виду с угловым коэффициентом ![]() (за исключением прямых, параллельных оси ординат).
(за исключением прямых, параллельных оси ординат).
Направляющий вектор прямой
Зададимся вопросом, что достаточно знать, чтобы построить прямую? Две точки. Но об этом детском случае позже, сейчас властвуют палочки со стрелочками. У каждой прямой есть вполне определённый наклон, к которому легко «приспособить» вектор.
Вектор, который параллелен прямой, называется направляющим вектором данной прямой. Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – не важно).
Направляющий вектор будем обозначать следующим образом: ![]() .
.
Сразу небольшая ремарка: при появлении трудностей в понимании терминов, пожалуйста, прочитайте (или перечитайте) статью Векторы для чайников.
Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости. Поэтому дополнительно нужно знать некоторую точку ![]() , которая принадлежит прямой.
, которая принадлежит прямой.
Как составить уравнение прямой по точке и направляющему вектору?
Если известна некоторая точка ![]() , принадлежащая прямой, и направляющий вектор
, принадлежащая прямой, и направляющий вектор ![]() этой прямой
этой прямой ![]() , то уравнение данной прямой можно составить по формуле:
, то уравнение данной прямой можно составить по формуле:
![]()
Иногда его называют каноническим уравнением прямой.
Что делать, когда одна из координат ![]() равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты не могут равняться нулю, так как нулевой вектор не задаёт конкретного направления.
равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты не могут равняться нулю, так как нулевой вектор не задаёт конкретного направления.
Пример 3
Составить уравнение прямой по точке ![]() и направляющему вектору
и направляющему вектору ![]()
Решение: уравнение прямой составим по формуле ![]() . В данном случае:
. В данном случае:
![]()
С помощью свойств пропорции избавляемся от дробей:
![]()
И приводим уравнение к общему виду:
![]()
Ответ: ![]()
Чертежа в таких примерах, как правило, делать не нужно, но понимания ради:
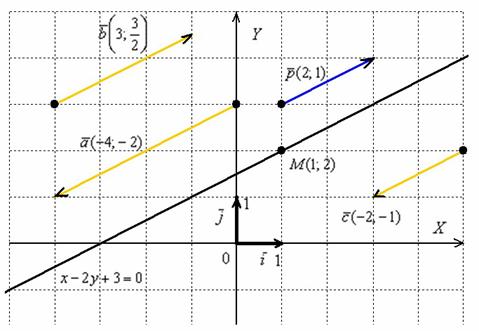
На чертеже мы видим исходную точку ![]() , исходный направляющий вектор
, исходный направляющий вектор ![]() (его можно отложить от любой точки плоскости) и построенную прямую
(его можно отложить от любой точки плоскости) и построенную прямую ![]() . Кстати, во многих случаях построение прямой удобнее всего осуществлять как раз с помощью уравнения с угловым коэффициентом. Наше уравнение
. Кстати, во многих случаях построение прямой удобнее всего осуществлять как раз с помощью уравнения с угловым коэффициентом. Наше уравнение ![]() легко преобразовать к виду
легко преобразовать к виду ![]() и без проблем подобрать ещё одну точку для построения прямой.
и без проблем подобрать ещё одну точку для построения прямой.
Как отмечалось в начале параграфа, у прямой бесконечно много направляющих векторов, и все они коллинеарны. Для примера я нарисовал три таких вектора: ![]() . Какой бы направляющий вектор мы не выбрали, в результате всегда получится одно и то же уравнение прямой
. Какой бы направляющий вектор мы не выбрали, в результате всегда получится одно и то же уравнение прямой ![]() .
.
Составим уравнение прямой по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
![]()
Разруливаем пропорцию:
![]()
Делим обе части на –2 и получаем знакомое уравнение: ![]()
Желающие могут аналогичным образом протестировать векторы ![]() или любой другой коллинеарный вектор.
или любой другой коллинеарный вектор.
Теперь решим обратную задачу:
как найти направляющий вектор по общему уравнению прямой?
Очень просто:
если прямая задана общим уравнением ![]() , то вектор
, то вектор ![]() является направляющим вектором данной прямой.
является направляющим вектором данной прямой.
Примеры нахождения направляющих векторов прямых:
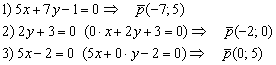
Утверждение позволяет найти лишь один направляющий вектор из бесчисленного множества, но нам больше и не нужно. Хотя, в ряде случаев координаты направляющих векторов целесообразно сократить:
Так, уравнение ![]() задаёт прямую, которая параллельна оси
задаёт прямую, которая параллельна оси ![]() , и координаты полученного направляющего вектора
, и координаты полученного направляющего вектора ![]() удобно разделить на –2, получая в точности базисный вектор
удобно разделить на –2, получая в точности базисный вектор ![]() в качестве направляющего вектора. Логично.
в качестве направляющего вектора. Логично.
Аналогично, уравнение ![]() задаёт прямую, параллельную оси
задаёт прямую, параллельную оси ![]() , и, разделив координаты вектора
, и, разделив координаты вектора ![]() на 5, получаем в качестве направляющего вектора орт
на 5, получаем в качестве направляющего вектора орт ![]() .
.
Читателям с низким уровнем подготовки рекомендую постоянно выполнять чертежи, чтобы лучше понимать мои объяснения.
Теперь выполним проверку Примера 3. Решение уехало вверх, поэтому напоминаю, что в нём мы составили уравнение прямой ![]() по точке
по точке ![]() и направляющему вектору
и направляющему вектору ![]()
Во-первых, по уравнению прямой ![]() восстанавливаем её направляющий вектор:
восстанавливаем её направляющий вектор: ![]() – всё нормально, получили исходный вектор (в ряде случаев может получиться коллинеарный исходному вектор, и это обычно несложно заметить по пропорциональности соответствующих координат).
– всё нормально, получили исходный вектор (в ряде случаев может получиться коллинеарный исходному вектор, и это обычно несложно заметить по пропорциональности соответствующих координат).
Во-вторых, координаты точки ![]() должны удовлетворять уравнению
должны удовлетворять уравнению ![]() . Подставляем их в уравнение:
. Подставляем их в уравнение:
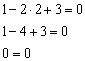
Получено верное равенство, чему мы очень рады.
Вывод: задание выполнено правильно.
Пример 4
Составить уравнение прямой по точке ![]() и направляющему вектору
и направляющему вектору ![]()
Это пример для самостоятельного решения. Решение и ответ в конце урока. Крайне желательно сделать проверку по только что рассмотренному алгоритму. Старайтесь всегда (если это возможно) выполнять проверку на черновике. Глупо допускать ошибки там, где их 100%-но можно избежать.
В том случае, если одна из координат направляющего вектора нулевая, поступают очень просто:
Пример 5
Составить уравнение прямой по точке ![]() и направляющему вектору
и направляющему вектору ![]() .
.
Решение: формула ![]() не годится, так как знаменатель правой части равен нулю. Выход есть! Используя свойства пропорции, перепишем формулу в виде
не годится, так как знаменатель правой части равен нулю. Выход есть! Используя свойства пропорции, перепишем формулу в виде ![]() , и дальнейшее покатилось по глубокой колее:
, и дальнейшее покатилось по глубокой колее:
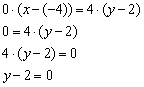
Ответ: ![]()
Проверка:
1) Восстановим направляющий вектор прямой ![]() :
:
![]() – полученный вектор коллинеарен исходному направляющему вектору.
– полученный вектор коллинеарен исходному направляющему вектору.
2) Подставим координаты точки ![]() в уравнение
в уравнение ![]() :
:
![]()
Получено верное равенство
Вывод: задание выполнено правильно.
Возникает вопрос, зачем маяться с формулой ![]() , если существует универсальная версия
, если существует универсальная версия ![]() , которая сработает в любом случае? Причин две. Во-первых, формула в виде дроби
, которая сработает в любом случае? Причин две. Во-первых, формула в виде дроби ![]() гораздо лучше запоминается. А во-вторых, недостаток универсальной формулы
гораздо лучше запоминается. А во-вторых, недостаток универсальной формулы ![]() состоит в том, что заметно повышается риск запутаться при подстановке координат.
состоит в том, что заметно повышается риск запутаться при подстановке координат.
Пример 6
Составить уравнение прямой по точке ![]() и направляющему вектору
и направляющему вектору ![]() .
.
Это пример для самостоятельного решения.
Вернёмся к «школьному» способу:
как составить уравнение прямой по двум точкам?
Если известны две точки ![]() , то уравнение прямой, проходящей через данные точки, можно составить по формуле:
, то уравнение прямой, проходящей через данные точки, можно составить по формуле:
![]()
На самом деле это разновидность формулы ![]() и вот почему: если известны две точки
и вот почему: если известны две точки ![]() , то вектор
, то вектор ![]() будет направляющим вектором данной прямой. На уроке Векторы для чайников мы рассматривали простейшую задачу – как найти координаты вектора по двум точкам. Согласно данной задаче, координаты направляющего вектора:
будет направляющим вектором данной прямой. На уроке Векторы для чайников мы рассматривали простейшую задачу – как найти координаты вектора по двум точкам. Согласно данной задаче, координаты направляющего вектора: ![]()
Примечание: точки можно «поменять ролями» и использовать формулу ![]() . Такое решение будет равноценным.
. Такое решение будет равноценным.
Пример 7
Составить уравнение прямой по двум точкам ![]() .
.
Решение: используем формулу:
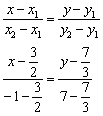
Причёсываем знаменатели:
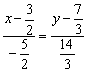
И перетасовываем колоду:
![]()
Именно сейчас удобно избавиться от дробных чисел. В данном случае нужно умножить обе части на 6:
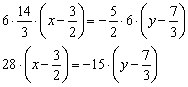
Раскрываем скобки и доводим уравнение до ума:
![]()
Ответ: ![]()
Проверка очевидна – координаты исходных точек должны удовлетворять полученному уравнению:
1) Подставим координаты точки ![]() :
:
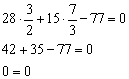
Верное равенство.
2) Подставим координаты точки ![]() :
:
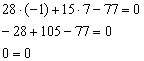
Верное равенство.
Вывод: уравнение прямой составлено правильно.
Если хотя бы одна из точек не удовлетворяет уравнению, ищите ошибку.
Стоит отметить, что графическая проверка в данном случае затруднительна, поскольку построить прямую ![]() и посмотреть, принадлежат ли ей точки
и посмотреть, принадлежат ли ей точки ![]() , не так-то просто.
, не так-то просто.
Отмечу ещё пару технических моментов решения. Возможно, в данной задаче выгоднее воспользоваться зеркальной формулой ![]() и, по тем же точкам
и, по тем же точкам ![]() составить уравнение:
составить уравнение:
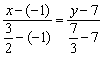
Таки дробей поменьше. Если хотите, можете довести решение до конца, в результате должно получиться то же самое уравнение.
Второй момент состоит в том, чтобы посмотреть на итоговый ответ и прикинуть, нельзя ли его ещё упростить? Например, если получилось уравнение ![]() , то здесь целесообразно сократить на двойку:
, то здесь целесообразно сократить на двойку: ![]() – уравнение будет задавать ту же самую прямую. Впрочем, это уже тема разговора о взаимном расположении прямых.
– уравнение будет задавать ту же самую прямую. Впрочем, это уже тема разговора о взаимном расположении прямых.
Получив ответ ![]() в Примере 7, я на всякий случай, проверил, не делятся ли ВСЕ коэффициенты уравнения на 2, 3 или 7. Хотя, чаще всего подобные сокращения осуществляются ещё по ходу решения.
в Примере 7, я на всякий случай, проверил, не делятся ли ВСЕ коэффициенты уравнения на 2, 3 или 7. Хотя, чаще всего подобные сокращения осуществляются ещё по ходу решения.
Пример 8
Составить уравнение прямой, проходящей через точки ![]() .
.
Это пример для самостоятельного решения, который как раз позволит лучше понять и отработать технику вычислений.
Аналогично предыдущему параграфу: если в формуле ![]() один из знаменателей (координата направляющего вектора) обращается в ноль, то переписываем её в виде
один из знаменателей (координата направляющего вектора) обращается в ноль, то переписываем её в виде ![]() . И снова заметьте, как неуклюже и запутанно она стала выглядеть. Не вижу особого смысла приводить практические примеры, поскольку такую задачу мы уже фактически прорешали (см. № 5, 6).
. И снова заметьте, как неуклюже и запутанно она стала выглядеть. Не вижу особого смысла приводить практические примеры, поскольку такую задачу мы уже фактически прорешали (см. № 5, 6).
Вектор нормали прямой (нормальный вектор)
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), причём все векторы нормали прямой будут коллинеарными (сонаправленными или нет – без разницы).
Разборки с ними будут даже проще, чем с направляющими векторами:
если прямая задана общим уравнением ![]() в прямоугольной системе координат, то вектор
в прямоугольной системе координат, то вектор ![]() является вектором нормали данной прямой.
является вектором нормали данной прямой.
Если координаты направляющего вектора ![]() приходится аккуратно «вытаскивать» из уравнения, то координаты вектора нормали
приходится аккуратно «вытаскивать» из уравнения, то координаты вектора нормали ![]() достаточно просто «снять».
достаточно просто «снять».
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
![]()
Приведу примеры с теми же уравнениями, что и для направляющего вектора:
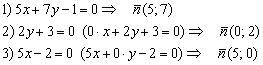
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Если известен вектор нормали, то однозначно определено и направление самой прямой – это «жёсткая конструкция» с углом в 90 градусов.
Как составить уравнение прямой по точке и вектору нормали?
Если известна некоторая точка ![]() , принадлежащая прямой, и вектор нормали
, принадлежащая прямой, и вектор нормали ![]() этой прямой, то уравнение данной прямой выражается формулой:
этой прямой, то уравнение данной прямой выражается формулой:
![]()
Тут всё обошлось без дробей и прочих нежданчиков. Такой вот у нас нормальный вектор. Любите его. И уважайте =)
Пример 9
Составить уравнение прямой по точке ![]() и вектору нормали
и вектору нормали ![]() . Найти направляющий вектор прямой.
. Найти направляющий вектор прямой.
Решение: используем формулу:
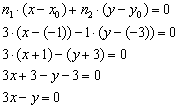
Общее уравнение прямой получено, выполним проверку:
1) «Снимаем» координаты вектора нормали с уравнения ![]() :
: ![]() – да, действительно, получен исходный вектор из условия (либо должен получиться коллинеарный исходному вектор).
– да, действительно, получен исходный вектор из условия (либо должен получиться коллинеарный исходному вектор).
2) Проверим, удовлетворяет ли точка ![]() уравнению
уравнению ![]() :
:
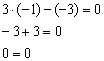
Верное равенство.
После того, как мы убедились в том, что уравнение составлено правильно, выполним вторую, более лёгкую часть задания. Вытаскиваем направляющий вектор прямой: ![]()
Ответ: ![]()
На чертеже ситуация выглядит следующим образом:
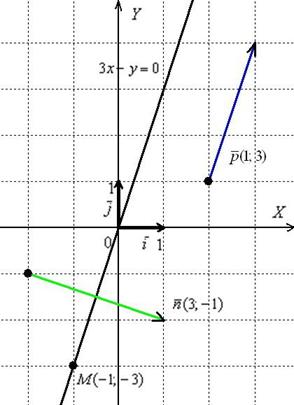
В целях тренировки аналогичная задача для самостоятельного решения:
Пример 10
Составить уравнение прямой по точке ![]() и нормальному вектору
и нормальному вектору ![]() . Найти направляющий вектор прямой.
. Найти направляющий вектор прямой.
Заключительный раздел урока будет посвящен менее распространённым, но тоже важным видам уравнений прямой на плоскости.
Уравнение прямой в отрезках
Уравнение прямой в отрезках имеет вид ![]() , где
, где ![]() – ненулевые константы. Некоторые типы уравнений нельзя представить в таком виде, например, прямую пропорциональность
– ненулевые константы. Некоторые типы уравнений нельзя представить в таком виде, например, прямую пропорциональность ![]() (так как свободный член
(так как свободный член ![]() равен нулю и единицу в правой части никак не получить).
равен нулю и единицу в правой части никак не получить).
Это, образно говоря, «технический» тип уравнения. Обыденная задача состоит в том, чтобы общее уравнение прямой ![]() представить в виде уравнения прямой в отрезках
представить в виде уравнения прямой в отрезках ![]() . Чем оно удобно? Уравнение прямой в отрезках позволяет быстро найти точки пересечения прямой с координатными осями, что бывает очень важным в некоторых задачах высшей математики.
. Чем оно удобно? Уравнение прямой в отрезках позволяет быстро найти точки пересечения прямой с координатными осями, что бывает очень важным в некоторых задачах высшей математики.
Найдём точку пересечения прямой с осью ![]() . Обнуляем «игрек», и уравнение принимает вид
. Обнуляем «игрек», и уравнение принимает вид ![]() . Нужная точка получается автоматически:
. Нужная точка получается автоматически: ![]() .
.
Аналогично с осью ![]() – точка, в которой прямая пересекает ось ординат.
– точка, в которой прямая пересекает ось ординат.
Действия, которые я только что подробно разъяснил, выполняются устно.
Пример 11
Дана прямая ![]() . Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.
. Составить уравнение прямой в отрезках и определить точки пересечения графика с координатными осями.
Решение: приведём уравнение к виду ![]() . Сначала перенесём свободный член в правую часть:
. Сначала перенесём свободный член в правую часть:
![]()
Чтобы получить справа единицу, разделим каждый член уравнения на –11:
![]()
Делаем дроби трёхэтажными:
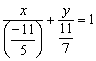
Точки пересечения прямой с координатными осями всплыли на поверхность:
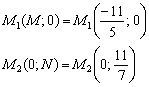
Ответ: 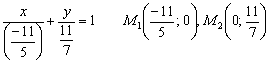
Осталось приложить линеечку и провести прямую.
Но я лучше в очередной раз напрягу Эксель:
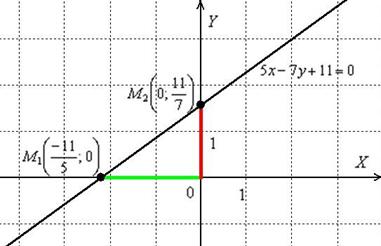
Легко усмотреть, что данная прямая однозначно определяется красным и зелёным отрезками, отсюда и название – «уравнение прямой в отрезках».
Конечно, точки ![]() не так трудно найти и из уравнения
не так трудно найти и из уравнения ![]() , но задача всё равно полезная. Рассмотренный алгоритм потребуется для нахождения точек пересечения плоскости с координатными осями, для приведения уравнения линии второго порядка к каноническому виду и в некоторых других задачах. Поэтому пара прямых для самостоятельного решения:
, но задача всё равно полезная. Рассмотренный алгоритм потребуется для нахождения точек пересечения плоскости с координатными осями, для приведения уравнения линии второго порядка к каноническому виду и в некоторых других задачах. Поэтому пара прямых для самостоятельного решения:
Пример 12
Составить уравнение прямой в отрезках и определить точки её пересечения с координатными осями.
а) ![]()
б) ![]()
Решения и ответы в конце урока. Не забывайте, что при желании всё можно начертить.
Уравнение прямой в параметрической форме,
и как его составить
Параметрические уравнения прямой больше актуальны для прямых в пространстве, но без «плоского» случая наш конспект бы осиротел.
Если известна некоторая точка ![]() , принадлежащая прямой, и направляющий вектор
, принадлежащая прямой, и направляющий вектор ![]() этой прямой, то параметрические уравнения данной прямой задаются системой:
этой прямой, то параметрические уравнения данной прямой задаются системой:
![]()
Что такое функция, заданная параметрически, я уже объяснял в статье Производная неявной и параметрически заданной функций. Но всё равно немного повторюсь в следующей демонстрационной задаче:
Пример 13
Составить параметрические уравнения прямой по точке ![]() и направляющему вектору
и направляющему вектору ![]()
Решение закончилось, не успев начаться:
![]()
Параметр «тэ» может принимать любые значения от «минус» бесконечности до «плюс» бесконечности, и каждому значению параметра соответствует конкретная точка плоскости. Например, если ![]() , то получаем точку
, то получаем точку ![]() .
.
Обратная задача: как проверить, будет ли точка ![]() условия принадлежать данной прямой?
условия принадлежать данной прямой?
Подставим координаты точки ![]() в полученные параметрические уравнения:
в полученные параметрические уравнения:
![]()
Из обоих уравнений следует, что ![]() , то есть система совместна и имеет единственное решение.
, то есть система совместна и имеет единственное решение.
Рассмотрим более содержательные задания:
Пример 14
Составить параметрические уравнения прямой ![]()
Решение: по условию прямая задана в общем виде. Для того чтобы составить параметрические уравнения прямой, нужно знать её направляющий вектор и какую-нибудь точку, принадлежащую данной прямой.
Найдём направляющий вектор: ![]()
Теперь нужно найти какую-нибудь точку, принадлежащую прямой (подойдёт любая), в этих целях общее уравнение удобно переписать в виде уравнения с угловым коэффициентом: ![]()
Напрашивается, конечно, точка ![]()
Составим параметрические уравнения прямой:
![]()
Ответ: ![]()
И напоследок небольшая творческая задача для самостоятельного решения.
Пример 15
Составить параметрические уравнения прямой, если известна принадлежащая ей точка ![]() и вектор нормали
и вектор нормали ![]()
Задачу можно оформить не единственным способом. Одна из версий решения и ответ в конце урока.
Существуют другие, более экзотические способы задать прямую, но то, что уже рассмотрено, хватит за глаза и за уши. Следующая статья, которую я рекомендую, называется Простейшие задачи с прямой на плоскости. В ней рассматриваются вещи, которые позволят окончательно укрепить ваш геометрический фундамент.
Желаю успехов!
Решения и ответы:
Пример 2. Решение: найдём угловой коэффициент:
![]()
Уравнение прямой составим по точке ![]() и угловому коэффициенту
и угловому коэффициенту ![]() :
:
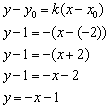
Ответ: ![]()
Пример 4. Решение: уравнение прямой составим по формуле:
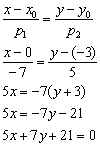
Ответ: ![]()
Пример 6. Решение: используем формулу:
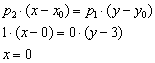
Ответ: ![]() (ось ординат)
(ось ординат)
Пример 8. Решение: составим уравнение прямой по двум точкам:
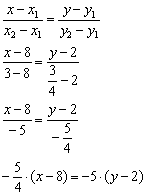
Умножаем обе части на –4:
![]()
И делим на 5:
![]()
Ответ: ![]()
Пример 10. Решение: используем формулу:
![]()
Сокращаем на –2:
![]()
Направляющий вектор прямой: ![]()
Ответ: ![]()
Пример 12. Решение:
а) Преобразуем уравнение:
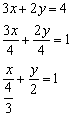
Таким образом:
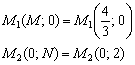
Ответ: 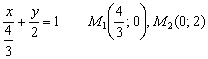
б) Преобразуем уравнение:
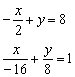
Таким образом:
![]()
Ответ: ![]()
Пример 15. Решение: сначала составим общее уравнение прямой по точке ![]() и вектору нормали
и вектору нормали ![]() :
:
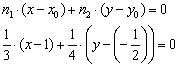
Умножаем на 12:
![]()
Умножаем ещё на 2, чтобы после раскрытия второй скобки избавиться от дроби:
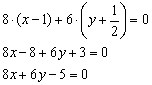
Направляющий вектор прямой: ![]()
Параметрические уравнения прямой составим по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
: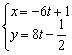
Ответ: 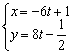
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright