


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Задачи с дифференциальными уравнениями
Ну а как иначе? Если есть дифференциальные уравнения, то должны быть и задачи с ними! Они встречаются в математике (само собой), физике, химии, других науках и, разумеется, соответствующих примеров великое множество – пятилетки не хватит, чтобы все их разобрать. Но этого и не нужно – сегодня наша цель освоить общие принципы решения таких задач, хотя,… штук 50-то всяко осилим)
Начнём с самого главного: вот видим мы текст задачи. Как определить, что её нужно решать с помощью ИМЕННО дифференциального уравнения? Очень просто. Поскольку корнями диффуров являются функции, то по условию так или иначе потребуется найти:
функцию / уравнение / линию / кривую / закон / зависимость и т. д.
В большинстве тематических задач фигурируют дифференциальные уравнения первого порядка, с них и начнём. Как вы прекрасно знаете, в оные уравнения обязательно входит первая производная, и поэтому для освоения урока нужно понимать (очевидно-невероятно), что такое производная. Впрочем, уважаемые студенты, пощады не ждите – я вам обязательно напомню =) И моя беспощадность такова, что мы займёмся этим прямо сейчас:
Задача 1
Кривая проходит через точку ![]() и обладает тем свойством, что угловой коэффициент касательной в любой её точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности
и обладает тем свойством, что угловой коэффициент касательной в любой её точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности ![]() . Найти уравнение этой кривой.
. Найти уравнение этой кривой.
Пожалуйста, типичный признак – условие запрашивает у нас уравнение кривой, а значит, задача решается с помощью дифференциального уравнения.
Решение: на первом шаге нужно это самое уравнение составить. Рассмотрим произвольную точку ![]() , принадлежащую искомой кривой. Заметьте, что этой хитрой фразой мы учитываем ВСЕ точки разыскиваемой линии.
, принадлежащую искомой кривой. Заметьте, что этой хитрой фразой мы учитываем ВСЕ точки разыскиваемой линии.
Выполним схематический чертёж, на котором изобразим некоторую кривую ![]() , произвольную точку
, произвольную точку ![]() и касательную
и касательную ![]() , проведённую к графику функции в данной точке:
, проведённую к графику функции в данной точке:
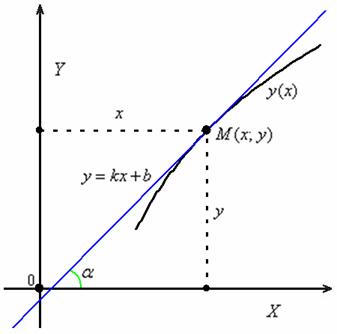
Теперь вспоминаем, что угловой коэффициент ![]() касательной равен тангенсу её угла наклона и равен значению производной в точке
касательной равен тангенсу её угла наклона и равен значению производной в точке ![]() :
:
![]()
Или, если короче: ![]()
По условию, угловой коэффициент касательной ![]() в любой точке
в любой точке ![]() кривой пропорционален квадрату ординаты («игрековой» координаты) точки касания:
кривой пропорционален квадрату ординаты («игрековой» координаты) точки касания:
![]() , где
, где ![]() – коэффициент пропорциональности.
– коэффициент пропорциональности.
(значок «тильда» обозначает пропорциональность)
В данной задаче ![]() . Таким образом, получаем следующее дифференциальное уравнение:
. Таким образом, получаем следующее дифференциальное уравнение:
![]() , которое, понятно, нужно решить :)
, которое, понятно, нужно решить :)
Перед нами ДУ с разделяющимися переменными:
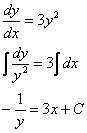
Общее решение: ![]()
В результате мы получили целое семейство функций, удовлетворяющих критерию задачи. Но в условии есть уточнение: кривая проходит через точку ![]() . Решим задачу Коши, т. е. найдём соответствующее частное решение. Здесь удобно непосредственно подставить в общее решение координаты
. Решим задачу Коши, т. е. найдём соответствующее частное решение. Здесь удобно непосредственно подставить в общее решение координаты ![]() точки:
точки:
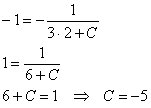
Таким образом, уравнение, искомой кривой:
![]()
Ответ: ![]()
Выполним проверку. Она проводится стандартно + желательный анализ, связанный с содержательным смыслом задачи.
Прежде всего, убедимся, что график полученной функции действительно проходит через точку ![]() :
:
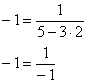
![]() – получено верное равенство, что и требовалось проверить.
– получено верное равенство, что и требовалось проверить.
Найдём производную:
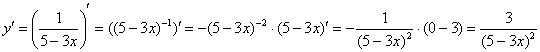
Подставим ![]() и
и ![]() в уравнение
в уравнение ![]() :
:
![]()
![]() – таким образом, частное решение найдено верно.
– таким образом, частное решение найдено верно.
Но это ещё не всё – ведь мы могли неправильно составить само дифференциальное уравнение! И поэтому будет не лишним вернуться условию, согласно которому, любая точка кривой ![]() должна обладать следующим свойством: производная функции в точке (угловой коэффициент касательной) равна утроенному квадрату «игрековой» координаты данной точки. Рассмотрим ту же точку
должна обладать следующим свойством: производная функции в точке (угловой коэффициент касательной) равна утроенному квадрату «игрековой» координаты данной точки. Рассмотрим ту же точку ![]() и вычислим:
и вычислим:
![]()
С другой стороны, утроенный квадрат «игрековой» координаты точки ![]() :
:
![]() , отлично.
, отлично.
Желающие могут протестировать любую другую точку, принадлежащую кривой ![]() , например точку
, например точку ![]() , и убедиться в справедливости только что проверенного критерия. Это, кстати, легко сделать устно.
, и убедиться в справедливости только что проверенного критерия. Это, кстати, легко сделать устно.
Вот теперь-то задача «закрыта наглухо». Ну а то, что схематический чертёж далёк от графика гиперболы ![]() – совершенно не страшно, чертёж лишь помогает разобраться в условии. И строить его, к слову, в простых случаях совсем не обязательно ;) И в самом деле – этого же не требовалось….
– совершенно не страшно, чертёж лишь помогает разобраться в условии. И строить его, к слову, в простых случаях совсем не обязательно ;) И в самом деле – этого же не требовалось….
Пара типовых задач для самостоятельного решения:
Задача 2
Угловой коэффициент касательной к каждой точке кривой обратно пропорционален абсциссе точки касания с коэффициентом пропорциональности ![]() . Составить уравнение данной кривой, если известно, что она проходит через точку
. Составить уравнение данной кривой, если известно, что она проходит через точку ![]()
Как раз аналогичный пример, в котором вполне можно обойтись без чертежа. Напоминаю, что обратная пропорциональность устроена по принципу «чем больше – тем меньше» – это зависимость… где-то я о ней вроде упоминал…, да, нашёл – в статье о гиперболе. Впрочем, многие помнят этот материал со школы.
И тут ещё хочу предупредить о возможной «накладке» с обозначениями: в «реальных» примерах коэффициент пропорциональности очень часто обозначают буквой ![]() , что, конечно, не есть хорошо.
, что, конечно, не есть хорошо.
Примерный образец чистового оформления задания в конце урока.
Чуть потруднее:
Задача 3
Найти кривую, для которой тангенс угла наклона ее касательной в любой её точке в 2 раза больше тангенса угла наклона прямой, проходящей через ту же точку и начало координат.
А вот здесь уже чертёж не помешает – рассматриваем прямоугольный треугольник, на всякий пожарный: тангенс – это отношение противолежащего катета к прилежащему катету. Впрочем, «картинку» этой задачи опять же несложно «обработать в уме». Но в образце решения я не поленился и выполнил схематический чертёж. И таки догадайтесь, как правильно записать ответ – проанализируйте полученное решение на соответствие условию задачи ;)
Как видите, задачки вроде бы элементарные, а «подводных камней» в них хватает. И перед тем как перейти от «чистой математики» к приложениям (по физике, химии и т. д.) я рассмотрю пару «настоящих» примеров.
Во многих случаях вам придётся столкнуться с задачей из сборника А.П. Рябушко (Часть 2, ИДЗ 11.4, Задача № 4) или из сборника Кузнецова. Или же с какой-то похожей задачей.
Первый источник отличается меньшей сложностью, и что особо приятно, каждая из 30 задач снабжена правильным ответом. Однако здесь нужно помнить, что решение диффура обычно можно записать несколькими способами, и формально результаты могут не совпасть.
Примеры из задачника Л.А. Кузнецова (Раздел V Дифференциальные уравнения, Задача 9) более трудны, но зато по Интернету давным-давно «гуляют» готовые решения всех вариантов. Может быть, найдёте и свою задачу! Однако не спешите радоваться «халяве» и бездумно переписывать материалы – неточностей там хватает.
Гораздо выгоднее ОДИН РАЗ РАЗОБРАТЬСЯ в технике решения таких задач!
Я подробно остановлюсь на заданиях из вариантов 11-20 сборника Кузнецова, которые, как показывает практика, вызывают наибольшие затруднения у студентов, и разберу пример 12-го варианта, который, кстати, в указанном выше источнике вообще решён неправильно:
Задача 4
Найти линию, проходящую через точку ![]() , если отрезок любой ее касательной между точкой касания и осью
, если отрезок любой ее касательной между точкой касания и осью ![]() делится в точке пересечения с осью абсцисс в отношении
делится в точке пересечения с осью абсцисс в отношении ![]() (считая от оси
(считая от оси ![]() ).
).
Прежде всего, снова обратим внимание на то, что по условию требуется найти линию, следовательно, участь наша – дифференциальное уравнение. И, кроме того, речь идёт о касательной, которая, как вы уже вспомнили, определяется через производную.
Решение: должен предупредить, что здесь опять возникают «накладки» с обозначениями, и я буду придерживаться собственной версии оформления, которая показалась мне наиболее удобной. Сначала рассмотрим некоторую конкретную точку ![]() , принадлежащую искомой линии, и соответствующую касательную. Выполним схематический чертёж. Из условия задачи следует, что точка
, принадлежащую искомой линии, и соответствующую касательную. Выполним схематический чертёж. Из условия задачи следует, что точка ![]() пересечения касательной с осью
пересечения касательной с осью ![]() лежит строго между точек
лежит строго между точек ![]() и
и ![]() . Это принципиальный момент! – так бывает далеко не всегда. И, конечно, нужно постараться, чтобы отрезок
. Это принципиальный момент! – так бывает далеко не всегда. И, конечно, нужно постараться, чтобы отрезок ![]() был примерно в 2 раза длиннее отрезка
был примерно в 2 раза длиннее отрезка ![]() :
:
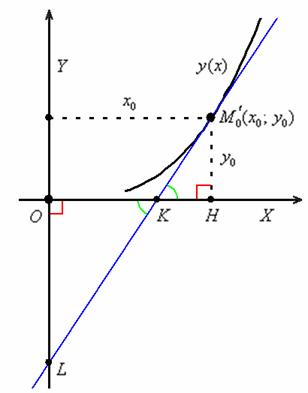
Первое, что приходит в голову – это найти длины отрезков ![]() и составить уравнение по формуле
и составить уравнение по формуле ![]() . Так решать можно…, но лучше не нужно. Вспоминаем школу: треугольники
. Так решать можно…, но лучше не нужно. Вспоминаем школу: треугольники ![]() и
и ![]() подобны по двум углам (обозначены красными и зелёными дугами), а значит, соответствующие стороны этих треугольников пропорциональны:
подобны по двум углам (обозначены красными и зелёными дугами), а значит, соответствующие стороны этих треугольников пропорциональны:
![]()
Грубо говоря, нижний треугольник в 2 раза больше, чем верхний.
В чём фишка? Фишка состоит в том, что длины отрезков ![]() найти значительно проще! Тем более, точки
найти значительно проще! Тем более, точки ![]() уже известны, и по существу, осталось найти «иксовую» координату точки
уже известны, и по существу, осталось найти «иксовую» координату точки ![]() . Находим:
. Находим:
Уравнение касательной к графику функции в точке ![]() имеет вид
имеет вид ![]() , и чтобы найти, где она пересекает ось абсцисс, нужно решить соответствующую систему линейных уравнений:
, и чтобы найти, где она пересекает ось абсцисс, нужно решить соответствующую систему линейных уравнений:
![]() , откуда выражаем «иксовую» координату точки «ка»:
, откуда выражаем «иксовую» координату точки «ка»:
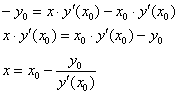
Таким образом: 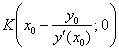
Для удобства запишу рабочие точки по порядку: 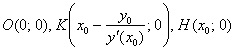
Теперь вернёмся к следующему моменту: изначально мы рассматривали некоторую конкретную точку ![]() , и сейчас настал черёд перейти к произвольной точке
, и сейчас настал черёд перейти к произвольной точке ![]() разыскиваемой линии. Проведём замены
разыскиваемой линии. Проведём замены ![]() :
:
![]()
! Примечание: этим приёмом я избежал технической «накладки» с буквами: сначала переменные ![]() обозначали, то, что они обычно обозначает, а после замен стали символизировать координаты произвольной точки
обозначали, то, что они обычно обозначает, а после замен стали символизировать координаты произвольной точки ![]() , принадлежащей искомой кривой.
, принадлежащей искомой кривой.
Длины отрезков ![]() можно найти по стандартной формуле длины отрезка, но опять – зачем нам нагромождения корней? Длина отрезка
можно найти по стандартной формуле длины отрезка, но опять – зачем нам нагромождения корней? Длина отрезка ![]() , очевидно, равна модулю его «иксовой» координаты (по той причине, что она может быть и отрицательна – отобразите чертёж симметрично относительно оси
, очевидно, равна модулю его «иксовой» координаты (по той причине, что она может быть и отрицательна – отобразите чертёж симметрично относительно оси ![]() ):
):
![]()
Длину второго отрезка найдём как разность «иксовых» координат точек ![]() и
и ![]() , которую из тех же соображений заключим под знак модуля:
, которую из тех же соображений заключим под знак модуля:
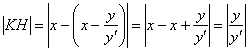
В соответствии с обоснованной выше пропорцией ![]() , составим дифференциальное уравнение. Удобнее сразу записать так:
, составим дифференциальное уравнение. Удобнее сразу записать так:
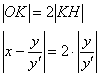
Сначала раскроем левый модуль:
![]()
При избавлении от правого модуля дробь может получиться как положительной, так и отрицательной, и поэтому всё так и останется:
![]()
В результате у нас получилось два дифференциальных уравнения:
![]()
Условию задачи удовлетворяет первое уравнение. Почему? Давайте посмотрим на чертёж: на нём координаты точек ![]() положительны, и для этого частного расположения точек мы получаем непосредственно уравнение
положительны, и для этого частного расположения точек мы получаем непосредственно уравнение ![]() (проведите рассуждения без модулей). Теперь мысленно отобразите чертёж симметрично относительно оси
(проведите рассуждения без модулей). Теперь мысленно отобразите чертёж симметрично относительно оси ![]() . Координаты точек
. Координаты точек ![]() станут отрицательными, и в результате «зеркальных» выкладок мы придём к уравнению
станут отрицательными, и в результате «зеркальных» выкладок мы придём к уравнению ![]() , т. е. к тому же самому уравнению, которое и соответствует геометрической ситуации нашей задачи (в нижней полуплоскости получаются 2 аналогичных случая).
, т. е. к тому же самому уравнению, которое и соответствует геометрической ситуации нашей задачи (в нижней полуплоскости получаются 2 аналогичных случая).
Вообще, при оформлении практической задачи обо всех этих тонкостях лучше аккуратно умолчать =) и сразу приступить к решению нужного уравнения:
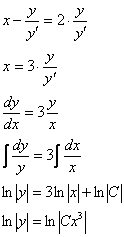
Общее решение: ![]()
По условию, линия должна проходить через точку ![]() . Решим задачу Коши:
. Решим задачу Коши:
![]()
Ответ: ![]() – искомая линия.
– искомая линия.
Как я отмечал выше, задачу можно разрулить и через «очевидное» отношение ![]() , но вычисления получатся просто хардкорными, а результат тот же самый – короткое равенство с двумя модулями.
, но вычисления получатся просто хардкорными, а результат тот же самый – короткое равенство с двумя модулями.
Желающие могут выполнить чертёж в масштабе 1ед. = 2 тетрадные клетки – изобразить кубическую параболу, удобную касательную и всё измерить линеечкой =) Улыбка улыбкой, но это, кстати, может пригодиться, если вы запутаетесь в модулях и будете сомневаться, какой диффур выбрать. Так или иначе, чертёж довольно прост:
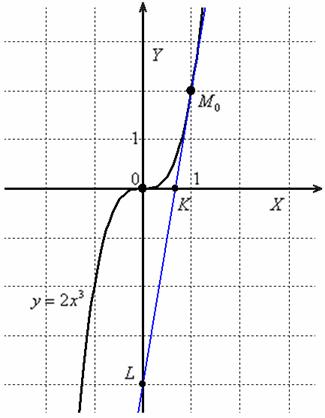
И в самом деле: ![]() . Аналогичное соотношение справедливо для любой касательной за исключением касательной в точке
. Аналогичное соотношение справедливо для любой касательной за исключением касательной в точке ![]() (оси абсцисс).
(оси абсцисс).
Примечание: здесь не возникает противоречия с условием задачи, в котором предполагается, что касательная пересекает координатные оси в разных точках.
А теперь разберём побочный диффур, который нарисовался в ходе решения:
Общее решение: ![]()
Решим задачу Коши для точки ![]() :
:
![]()
Таким образом, получаем гиперболу ![]() . Следует заметить, что здесь тоже выполнено соотношение
. Следует заметить, что здесь тоже выполнено соотношение ![]() , нарисую «на скорую руку» одну ветку:
, нарисую «на скорую руку» одну ветку:
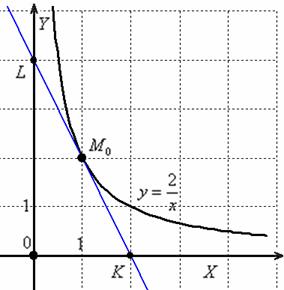
Однако геометрическая ситуация совершенно другая – касательная пересекает координатные оси по разные стороны от точки касания.
Для этого случая условие можно сформулировать несколько по-другому: Найти линию, проходящую через точку ![]() , если отрезок любой ее касательной, заключенный между осями координат, делится в точке касания в отношении
, если отрезок любой ее касательной, заключенный между осями координат, делится в точке касания в отношении ![]() . И такому расположению касательной посвящены задачи 16-20 сборника Кузнецова.
. И такому расположению касательной посвящены задачи 16-20 сборника Кузнецова.
Энтузиасты могут прорешать эту, более простую задачу по трафарету. И, конечно, в ней тоже не надо находить длины отрезков ![]() и
и ![]() – намного выгоднее снова рассмотреть подобные треугольники (которые расположены один над другим и так оказалось, что вообще равны). Интересно, что в ходе решения опять появятся два диффура, из которых потребуется выбрать «правильный».
– намного выгоднее снова рассмотреть подобные треугольники (которые расположены один над другим и так оказалось, что вообще равны). Интересно, что в ходе решения опять появятся два диффура, из которых потребуется выбрать «правильный».
Для самостоятельного решения также предлагаю ещё одно задание:
Задача 5
Найти линию, проходящую через точку ![]() и обладающую тем свойством, что в любой её точке
и обладающую тем свойством, что в любой её точке ![]() нормальный вектор
нормальный вектор ![]() с концом на оси
с концом на оси ![]() имеет длину, равную
имеет длину, равную ![]() , и отрезок
, и отрезок ![]() образует острый угол с положительным направлением оси
образует острый угол с положительным направлением оси ![]() .
.
Систематизируем схему решения:
1) Во избежание неразберихи с «иксом» и «игреком» рассматриваем некоторую конкретную точку ![]() , принадлежащую искомой прямой. Вообще говоря, можно сразу работать с произвольной точкой
, принадлежащую искомой прямой. Вообще говоря, можно сразу работать с произвольной точкой ![]() , но тогда «глобальные» переменные придётся обозначить как-нибудь по-другому, например, через
, но тогда «глобальные» переменные придётся обозначить как-нибудь по-другому, например, через ![]() .
.
2) Составляем уравнение нормали, проходящей через точку ![]() .
.
3) Находим координаты точки ![]() пересечения нормали с осью ординат.
пересечения нормали с осью ординат.
4) Находим длину вектора ![]() . А вот здесь уже без корня обойтись трудно.
. А вот здесь уже без корня обойтись трудно.
5) Теперь переходим к рассмотрению произвольной точки ![]() , т. е. выполняем замены
, т. е. выполняем замены ![]() . Этот шаг можно выполнить и чуть раньше (до нахождения длины вектора).
. Этот шаг можно выполнить и чуть раньше (до нахождения длины вектора).
6) Составляем и решаем дифференциальное уравнение. В ходе решения используем информацию о том, что отрезок ![]() образует острый угол с положительным направлением оси
образует острый угол с положительным направлением оси ![]() .
.
Однако здесь существует и более короткое решение, которым поделилась одна из читательниц сайта. В своё время (когда создавалась статья) из моего поле зрения выпала эта элементарная возможность, и поэтому в конце урока я, конечно же, добавил 2-й способ. Постарайтесь его увидеть! И спасибо за ваши письма – они действительно помогают улучшить учебные материалы.
Я не сторонник различного рода справочников, но для решения практических задач могут пригодиться следующие готовые формулы:
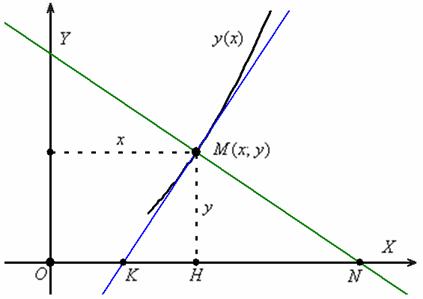
Длина отрезка касательной: ![]()
Подкасательная: ![]()
Длина отрезка нормали: ![]()
Поднормаль: ![]()
Но всё же старайтесь их выводить по ходу решения той или иной задачи.
Поскольку сайт посвящен математике, то бОльшую часть урока заняла математика =), но, разумеется, я не могу обойти стороной многочисленные прикладные задачи, которые рассматриваются даже в школе. Их часто (и может быть даже корректнее) называют задачами, которые ПРИВОДЯТ к понятию дифференциального уравнения. Отличительной особенностью этих задач (как правило) является тот факт, что условие опирается на сам СМЫСЛ производной, то есть речь в нём идёт о скорости изменения некоторого показателя.
Физика, химия,… да чего тут занудничать – биология:
Задача 6
Требуется составить дифференциальное уравнение динамики развития некоторого биологического вида и найти решение этого уравнения.
Состояние популяции можно охарактеризовать массой ![]() этой популяции (весом всего стада), причем масса является функцией времени
этой популяции (весом всего стада), причем масса является функцией времени ![]() . Считая, что скорость роста биомассы пропорциональна биомассе популяции с коэффициентом пропорциональности
. Считая, что скорость роста биомассы пропорциональна биомассе популяции с коэффициентом пропорциональности ![]() , найти массу стада в момент времени
, найти массу стада в момент времени ![]() , если известно её значение
, если известно её значение ![]() при
при ![]() .
.
…Надо сказать, автор задачи не стал мучить студентов-зоотехников и расписал всё подробнейшим образом. Давайте, тем не менее, остановимся на характерных признаках, позволяющих определить, что тут замешано дифференциальное уравнение:
– во-первых, нам явно придётся отыскать функцию ![]() массы стада, зависящую от времени;
массы стада, зависящую от времени;
– и, во-вторых, в условии прямо сказано о скорости роста этой самой массы.
А за скорость роста у нас отвечает производная функция, в данном случае функция ![]()
На самом деле решение очень простое и напоминает оно 1-ю задачу урока. По условию, скорость изменения массы стада пропорциональна этой массе:
![]()
В большинстве практических задач коэффициент пропорциональности равен константе, но вот здесь он представляет собой функцию: ![]() . Впрочем, это не имеет особого значения:
. Впрочем, это не имеет особого значения:
![]()
Разделяем и властвуем:
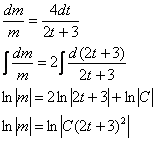
Общее решение: ![]()
По условию, в момент времени ![]() биомасса составляет
биомасса составляет ![]() . Решим задачу Коши:
. Решим задачу Коши:
![]()
Таким образом, закон изменения массы популяции:
![]()
Шустрая, однако, популяция – прямо какое-то стадо кроликов… или даже саранчи. …Хотя в задаче ничего не сказано о размерности величин. И поэтому, кстати, здесь будет корректно говорить о единицах времени и единицах массы.
Найдём то, что требовалось найти:
![]() – масса стада в момент времени
– масса стада в момент времени ![]()
Ответ: ![]()
…Наверное, вы ждёте - не дождетесь задач по физике…. Спешу обнадёжить вас принципом «антиРабиновича»: Дождётесь! =) Но перед этим примем йаду таблеточку:
Задача 7
Таблетка массой 0,5 г брошена в стакан воды. Скорость растворения таблетки пропорциональна массе таблетки. Через какое время растворится 99% вещества, если известно, что через 10 минут растворилось 80%?
Это очень простая… и не простая задача ;) Постарайтесь самым тщательным образом разобраться в решении, задач в подобном техническом исполнении намного больше стакана – их пруд пруди. И кто позабыл – свойства степеней и логарифмов в помощь.
К сожалению, нельзя объять необъятное, и около 10 готовых задач по физике я загрузил в библиотеку, в основном, там задачи по механике. Физика не является моим профильным предметом, но вроде получилось неплохо….
Что касается дифуров 2-го и более высоких порядков, то на практике они встречаются намного реже. Здесь можно отметить задачи на 2-й закон Ньютона (через ДУ, допускающее понижение порядка – см. по ссылке выше), а также задачу о свободных и вынужденных колебаниях (линейные ОДУ и НДУ 2-го порядка). Теоретический материал по последней задаче можно посмотреть здесь.
Спасибо за внимание – надеюсь, урок был полезен, и теперь вы сможете справиться с любой тематической задачей!
Решения и ответы:
Задача 2. Решение: рассмотрим произвольную точку ![]() , принадлежащую искомой кривой. По условию, угловой коэффициент касательной к кривой в данной точке:
, принадлежащую искомой кривой. По условию, угловой коэффициент касательной к кривой в данной точке:
![]()
Учитывая, что ![]() и
и ![]() , получаем следующее дифференциальное уравнение:
, получаем следующее дифференциальное уравнение:
![]()
Разделяем переменные и интегрируем:

Общее решение: ![]() .
.
Найдём кривую, которая проходит через точку ![]() . Решим задачу Коши:
. Решим задачу Коши:
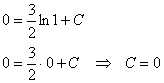
Ответ: ![]()
Задача 3. Решение: рассмотрим произвольную точку ![]() , принадлежащую искомой кривой, и соответствующую касательную:
, принадлежащую искомой кривой, и соответствующую касательную:
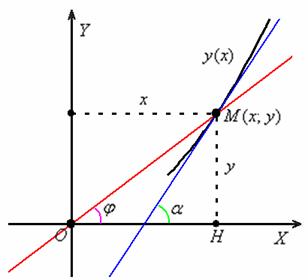
Согласно геометрическому смыслу производной: ![]() .
.
Проведём прямую ![]() и рассмотрим прямоугольный треугольник
и рассмотрим прямоугольный треугольник ![]() . По определению тангенса:
. По определению тангенса:
![]()
По условию задачи:
![]()
Таким образом, получаем следующее дифференциальное уравнение:
![]()
Разделяем переменные и интегрируем:
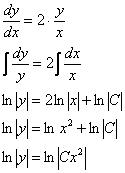
Общее решение: ![]()
Поскольку уравнение ![]() (ось абсцисс) не удовлетворяет условию задачи, то значение
(ось абсцисс) не удовлетворяет условию задачи, то значение ![]() следует исключить из множества решений.
следует исключить из множества решений.
Ответ: семейство парабол: ![]()
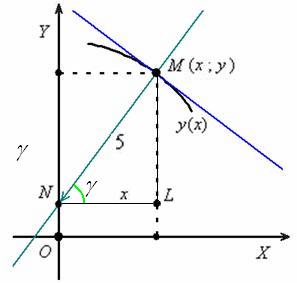
Задача 5. Решение: рассмотрим некоторую точку ![]() , принадлежащую искомой линии. Выполним схематический чертёж:
, принадлежащую искомой линии. Выполним схематический чертёж:
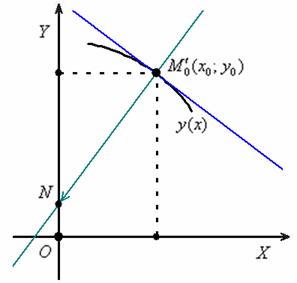
Составим уравнение нормали, проходящей через точку ![]() :
:
![]()
Найдём точку ![]() пересечения нормали с осью ординат:
пересечения нормали с осью ординат:
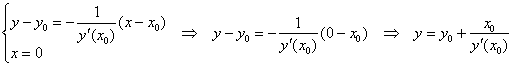
Таким образом: 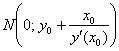
Вычислим длину вектора:
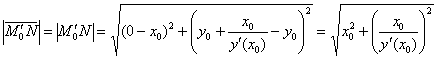
Рассмотрим произвольную точку ![]() , принадлежащую искомой кривой:
, принадлежащую искомой кривой:
![]()
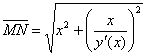
По условию:
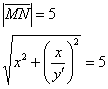
Возведём обе части в квадрат и выполним дальнейшие преобразования:

Так как отрезок ![]() образует острый угол с положительным направлением оси
образует острый угол с положительным направлением оси ![]() , то выбираем верхнюю полуокружность:
, то выбираем верхнюю полуокружность:
![]()
Решим задачу Коши для точки ![]() :
:
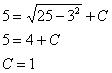
Ответ: ![]()
Второй способ решения: пусть точка ![]() , принадлежит искомой кривой:
, принадлежит искомой кривой:
Рассмотрим прямоугольный треугольник ![]() . По теореме Пифагора:
. По теореме Пифагора:
![]()
Таким образом, тангенс угла наклона нормали:
![]()
У перпендикулярных прямых угловые коэффициенты взаимнообратны и противоположны по знаку (см. статью Задачи с прямой), поэтому тангенс угла наклона касательной:
![]()
Разделяем переменные и интегрируем:

Решим задачу Коши для точки ![]() :
:
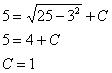
Ответ: ![]()
Задача 7. Решение: рассмотрим функцию ![]() изменения массы таблетки. В соответствии с условием:
изменения массы таблетки. В соответствии с условием:
![]() (коэффициент пропорциональности пока не известен)
(коэффициент пропорциональности пока не известен)
Разделяем переменные и интегрируем:

Примечание: здесь выполнено преобразование ![]() с последующим переобозначением константы:
с последующим переобозначением константы: ![]() .
.
В начальный момент времени масса таблетки составляла 0,5 г. Решим задачу Коши:
![]()
В результате: ![]()
Известно, что через 10 минут растворилось 80% таблетки, т. е. осталось ![]() г твёрдого вещества. Найдём значение параметра:
г твёрдого вещества. Найдём значение параметра:
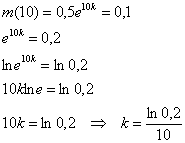
Таким образом: ![]() – закон изменения массы (растворения) таблетки.
– закон изменения массы (растворения) таблетки.
Найдём, через какое время растворится 99% таблетки. Поскольку твёрдого вещества останется ![]() г, то:
г, то:
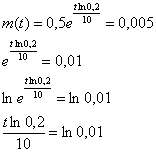
![]() мин.
мин.
Ответ: примерно через 28,6 мин
И в этой задаче один из читателей предположил, что полученное ДУ не учитывает полную растворимость таблетки. На самом деле учитывает. Случаю полной растворимости соответствует масса одной молекулы (если это однородное вещество), но такая точность нужна разве что в квантовой лаборатории :) В большинстве прикладных задач за полную растворимость достаточно принять, например, 99,9% растворённого вещества.
Спасибо за вашу любознательность и за ваши письма!
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright