


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Однородные системы линейных алгебраических уравнений
В рамках уроков метод Гаусса и Несовместные системы/системы с общим решением мы рассматривали неоднородные системы линейных уравнений, где свободный член (который обычно находится справа) хотя бы одного из уравнений был отличен от нуля.
И сейчас, после хорошей разминки с рангом матрицы, мы продолжим шлифовать технику элементарных преобразований на однородной системе линейных уравнений.
По первым абзацам материал может показаться скучным и заурядным, однако данное впечатление обманчиво. Помимо дальнейшей отработки технических приёмов будет много новой информации, поэтому, пожалуйста, постарайтесь не пренебрегать примерами данной статьи.
Что такое однородная система линейных уравнений?
Ответ напрашивается сам собой. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:
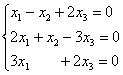
Совершенно ясно, что однородная система всегда совместна, то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое тривиальное решение ![]() . Тривиальное, для тех, кто совсем не понял смысл прилагательного, значит, беспонтовое. Не академично, конечно, но зато доходчиво =) …Чего ходить вокруг да около, давайте выясним, нет ли у данной системы каких-нибудь других решений:
. Тривиальное, для тех, кто совсем не понял смысл прилагательного, значит, беспонтовое. Не академично, конечно, но зато доходчиво =) …Чего ходить вокруг да около, давайте выясним, нет ли у данной системы каких-нибудь других решений:
Пример 1
Решить однородную систему линейных уравнений
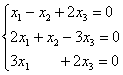
Решение: чтобы решить однородную систему нужно записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь не имеет смысла записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:

(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3.
(2) К третьей строке прибавили вторую строку, умноженную на –1.
Делить третью строку на 3 не имеет особого смысла.
В результате элементарных преобразований получена эквивалентная однородная система 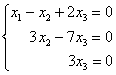 , и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.
, и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.
Ответ: ![]()
Сформулируем очевидный критерий: однородная система линейных уравнений имеет только тривиальное решение, если ранг матрицы системы (в данном случае 3) равен количеству переменных (в данном случае ![]() – 3 шт.).
– 3 шт.).
Разогреваемся и настраиваем свой радиоприёмник на волну элементарных преобразований:
Пример 2
Решить однородную систему линейных уравнений
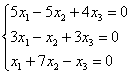
Из статьи Как найти ранг матрицы? вспоминаем рациональный приём попутного уменьшения чисел матрицы. В противном случае вам придётся разделывать крупную, а частенько и кусачую рыбу. Примерный образец оформления задания в конце урока.
Нули – это хорошо и удобно, однако на практике гораздо более распространен случай, когда строки матрицы системы линейно зависимы. И тогда неизбежно появление общего решения:
Пример 3
Решить однородную систему линейных уравнений
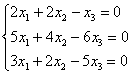
Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду. Первое действие направлено не только на получение единичного значения, но и на уменьшение чисел в первом столбце:
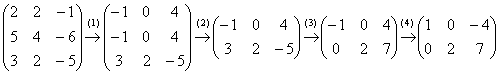
(1) К первой строке прибавили третью строку, умноженную на –1. Ко второй строке прибавили третью строку, умноженную на –2. Слева вверху я получил единицу с «минусом», что зачастую намного удобнее для дальнейших преобразований.
(2) Первые две строки одинаковы, одну из них удалили. Честное слово, не подгонял решение – так получилось. Если выполнять преобразования шаблонно, то линейная зависимость строк обнаружилась бы чуть позже.
(3) К третьей строке прибавили вторую строку, умноженную на 3.
(4) У первой строки сменили знак.
В результате элементарных преобразований получена эквивалентная система:
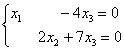
Алгоритм работает точно так же, как и для неоднородных систем. Переменные ![]() , «сидящие на ступеньках» – главные, переменная
, «сидящие на ступеньках» – главные, переменная ![]() , которой не досталось «ступеньки» – свободная.
, которой не досталось «ступеньки» – свободная.
Выразим базисные переменные через свободную переменную:
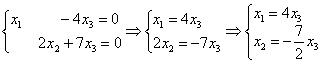
Ответ: общее решение: ![]()
Тривиальное решение входит в общую формулу, и записывать его отдельно излишне.
Проверка выполняется тоже по обычной схеме: полученное общее решение нужно подставить в левую часть каждого уравнения системы и получить законный ноль при всех подстановках.
На этом можно было бы тихо-мирно закончить, но решение однородной системы уравнений часто требуется представить в векторной форме с помощью фундаментальной системы решений. Пожалуйста, временно забудьте об аналитической геометрии, поскольку сейчас речь пойдёт о векторах в алгебраическом смысле, который я немного приоткрыл в статье про ранг матрицы и окончательно расписал на уроке о линейных преобразованиях. Терминологии тушеваться не нужно, всё довольно просто:
Фундаментальная система решений однородной системы уравнений
Фундаментальная система решений – это множество линейно независимых векторов ![]() , каждый из которых является решением однородной системы, кроме того, решением также является линейная комбинация данных векторов
, каждый из которых является решением однородной системы, кроме того, решением также является линейная комбинация данных векторов ![]() , где
, где ![]() – произвольные действительные числа.
– произвольные действительные числа.
Количество векторов ![]() фундаментальной системы рассчитывается по формуле:
фундаментальной системы рассчитывается по формуле:
![]()
Однако в практических заданиях гораздо удобнее ориентироваться на следующий признак: количество векторов ![]() фундаментальной системы равно количеству свободных переменных.
фундаментальной системы равно количеству свободных переменных.
Представим общее решение Примера № 3 ![]() в векторной форме. Свободная переменная в данном случае одна, поэтому фундаментальная система решений состоит из единственного вектора
в векторной форме. Свободная переменная в данном случае одна, поэтому фундаментальная система решений состоит из единственного вектора ![]() . Как его найти? Для этого свободной переменной нужно придать произвольное ненулевое значение. Проще всего, конечно же, выбрать
. Как его найти? Для этого свободной переменной нужно придать произвольное ненулевое значение. Проще всего, конечно же, выбрать ![]() и получить:
и получить: ![]() .
.
Координаты вектора ![]() должны удовлетворять каждому уравнению системы, и будет не лишним в этом убедиться.
должны удовлетворять каждому уравнению системы, и будет не лишним в этом убедиться.
Ответ следует записать в виде линейной комбинации векторов фундаментальной системы. В нашей ситуации линейная комбинация состоит из одинокого слагаемого. Общее решение однородной системы я буду обозначать через вектор ![]() (подстрочный индекс расшифровывается «Общее Однородной»).
(подстрочный индекс расшифровывается «Общее Однородной»).
Ответ: общее решение: ![]() , где
, где ![]() (любое вещественное число)
(любое вещественное число)
Придавая параметру ![]() различные действительные значения, можно получить бесконечно много частных решений, например, если
различные действительные значения, можно получить бесконечно много частных решений, например, если ![]() , то вектор частного решения однородного уравнения («Частное Однородной») равен:
, то вектор частного решения однородного уравнения («Частное Однородной») равен:
![]() , то есть набор переменных
, то есть набор переменных ![]() удовлетворяет каждому уравнению системы.
удовлетворяет каждому уравнению системы.
Это мы рассмотрели традиционный способ построения фундаментальной системы в так называемом нормальном виде – когда свободным переменным придаются исключительно единичные значения. Но правила хорошего математического тона предписывают избавляться от дробей, если это возможно. Поэтому в данном случае можно взять ![]() и из общего решения системы
и из общего решения системы ![]() получить вектор с целыми координатами:
получить вектор с целыми координатами: ![]()
И тогда ответ запишется в эквивалентной форме:
![]() , где
, где ![]() (любое вещественное число)
(любое вещественное число)
Оба варианта ответа правильны, однако чайникам я всё-таки рекомендую классику жанра.
Поблагодарим задачник Рябушко за предоставленные примеры и перейдём к более основательным системам:
Пример 4
Решить однородную систему линейных уравнений
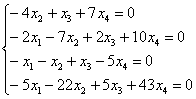
Ответ записать с помощью фундаментальной системы решений
Самостоятельно, plz. Примерный образец оформления в конце урока.
Закинем в копилку знаний ещё один полезный факт:
Взаимосвязь решений неоднородной
и соответствующей однородной системы уравнений
Представьте двух близких родственниц: неоднородную систему (у которой хотя бы один свободный член отличен от нуля) и такую же систему – только с нулевыми свободными членами (то бишь, однородную систему). Нетрудно предположить, что если системы отличаются лишь столбцом свободных членов, то между их решениями должна существовать тесная связь. И это действительно так! Материал целесообразнее рассмотреть на конкретной задаче, которая, как и все другие, взята из реальной контрольной работы:
Пример 5
Дана система линейных алгебраических уравнений
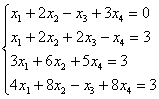
Требуется:
1) найти общее решение;
2) используя результат предыдущего пункта, найти общее решение соответствующей однородной системы и записать его в векторной форме.
Решение: по условию, дана обычная неоднородная система уравнений, и первая часть не отличается новизной:
1) Запишем расширенную матрицу системы (не зеваем нолик в третьей строке) и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на –3. К четвёртой строке прибавили первую строку, умноженную на –4.
(2) Последние три строки одинаковы, две из них удалили.
Обратным ходом метода Гаусса получим общее решение:
![]() – базисные переменные;
– базисные переменные;
![]() – свободные переменные.
– свободные переменные.
Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
![]() – подставим в 1-е уравнение:
– подставим в 1-е уравнение:
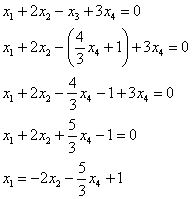
Общее решение неоднородной системы обозначим через ![]() («Общее Неоднородной»).
(«Общее Неоднородной»).
Ответ: ![]()
2) Во второй части задания требуется найти общее решение ![]() такой же, только однородной системы
такой же, только однородной системы 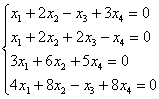 , причём, по условию, требуется использовать ответ предыдущего пункта.
, причём, по условию, требуется использовать ответ предыдущего пункта.
Выполнять элементарные преобразования заново, разумеется, не нужно.
Правило: общее решение неоднородной системы ![]() равно сумме общего решения соответствующей однородной системы
равно сумме общего решения соответствующей однородной системы ![]() и какого-либо частного решения неоднородной системы
и какого-либо частного решения неоднородной системы ![]() :
:
![]()
Откуда легко выражается общее решение нашей однородной системы:
![]()
Найдём какое-нибудь частное решение ![]() неоднородной системы. Проще всего взять нулевые значения свободных переменных
неоднородной системы. Проще всего взять нулевые значения свободных переменных ![]() :
:
![]()
Таким образом, общее решение соответствующей однородной системы:
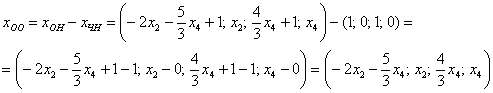
Представим ![]() в векторной форме. Поскольку у нас две свободные переменные, то фундаментальная система решений будет состоять из двух векторов.
в векторной форме. Поскольку у нас две свободные переменные, то фундаментальная система решений будет состоять из двух векторов.
Пойдём классическим путём:
Рассмотрим пару значений свободных переменных ![]() и получим первый вектор:
и получим первый вектор:
![]() – координаты данного вектора удовлетворяют каждому уравнению однородной системы (всегда желательна проверка!).
– координаты данного вектора удовлетворяют каждому уравнению однородной системы (всегда желательна проверка!).
Теперь рассматриваем пару ![]() и получаем второй вектор:
и получаем второй вектор:
![]() – координаты данного вектора также удовлетворяют каждому уравнению однородной системы (тоже проверяем!).
– координаты данного вектора также удовлетворяют каждому уравнению однородной системы (тоже проверяем!).
И вообще – любая линейная комбинация векторов фундаментальной системы ![]() , где
, где ![]() – произвольные действительные числа, является решением данной системы:
– произвольные действительные числа, является решением данной системы:
Ответ: ![]() , где
, где ![]()
Иными словами, если взять два любых вещественных числа, например, ![]() , то получится вектор частного решения однородной системы:
, то получится вектор частного решения однородной системы:
![]() , то есть набор
, то есть набор ![]() удовлетворяет каждому уравнению однородной системы.
удовлетворяет каждому уравнению однородной системы.
Если хотите избежать дробей, то при нахождении вектора ![]() следует выбрать значения
следует выбрать значения ![]() и получить второй вектор в виде:
и получить второй вектор в виде:
![]()
В этом случае ответ запишется в эквивалентной форме:
![]() , где
, где ![]()
Порядком многих я, наверное, подзапутал, но коль скоро задание не придумано, то его нельзя было обойти стороной.
Более распространённая тема для самостоятельного решения:
Пример 6
Дана однородная система
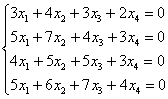
Найти общее решение и записать ответ с помощью векторов фундаментальной системы. В образце решения завершающим элементарным преобразованием я уже потихоньку начинаю приобщать вас к методу Гаусса-Жордана.
Чтобы окончательно закрепить алгоритм, разберём финальное задание:
Пример 7
Решить однородную систему, ответ записать в векторной форме.
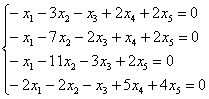
Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) У первой строки сменили знак. Ещё раз заостряю внимание на неоднократно встречавшемся приёме, который позволяет существенно упростить следующее действие.
(1) Ко 2-й и 3-й строкам прибавили первую строку. К 4-й строке прибавили первую строку, умноженную на 2.
(3) Последние три строки пропорциональны, две из них удалили.
В результате получена стандартная ступенчатая матрица, и решение продолжается по накатанной колее:
![]() – базисные переменные;
– базисные переменные;
![]() – свободные переменные.
– свободные переменные.
Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
![]() – подставим в 1-е уравнение:
– подставим в 1-е уравнение:
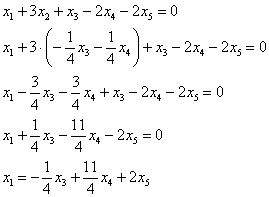
Таким образом, общее решение:
![]()
Поскольку в рассматриваемом примере три свободные переменные, то фундаментальная система содержит три вектора.
Подставим тройку значений ![]() в общее решение и получим вектор
в общее решение и получим вектор ![]() , координаты которого удовлетворяют каждому уравнению однородной системы. И снова повторюсь, что крайне желательно проверять каждый полученный вектор – времени займет не так много, а от ошибок убережёт стопроцентно.
, координаты которого удовлетворяют каждому уравнению однородной системы. И снова повторюсь, что крайне желательно проверять каждый полученный вектор – времени займет не так много, а от ошибок убережёт стопроцентно.
Для тройки значений ![]() находим вектор
находим вектор
![]()
И, наконец, для тройки ![]() получаем третий вектор:
получаем третий вектор:
![]()
Ответ: ![]() , где
, где ![]()
Желающие избежать дробных значений могут рассмотреть тройки ![]() и получить ответ в эквивалентном виде:
и получить ответ в эквивалентном виде:
![]()
К слову о дробях. Посмотрим на полученную в задаче матрицу ![]() и зададимся вопросом – нельзя ли упростить дальнейшее решение? Ведь здесь мы сначала выразили через дроби базисную переменную
и зададимся вопросом – нельзя ли упростить дальнейшее решение? Ведь здесь мы сначала выразили через дроби базисную переменную ![]() , потом через дроби базисную переменную
, потом через дроби базисную переменную ![]() , и, надо сказать, процесс это был не самый простой и не самый приятный.
, и, надо сказать, процесс это был не самый простой и не самый приятный.
Второй вариант решения:
Идея состоит в том, чтобы попытаться выбрать другие базисные переменные. Посмотрим на матрицу и заметим две единицы в третьем столбце. Так почему бы не получить ноль вверху? Проведём ещё одно элементарное преобразование:
![]()
(4) К первой строке прибавили вторую строку, умноженную на –1.
Здесь базисные переменные ![]() легко и практически мгновенно выражаются через свободные переменные
легко и практически мгновенно выражаются через свободные переменные ![]() :
:
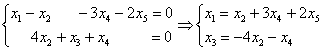
По существу, мы применили метод Гаусса-Жордана, который как раз и направлен на скорейшее получение базисного решения посредством дополнительных элементарных преобразований.
В результате общее решение: ![]()
Последовательно выбираем в качестве значений свободных переменных тройки
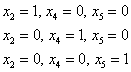
и подстановкой их в ![]() получаем соответствующие векторы фундаментальной системы:
получаем соответствующие векторы фундаментальной системы:
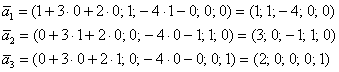
Не забываем проверить координаты каждого вектора!
Ответ: общее решение:
![]() , где
, где ![]() – действительные числа.
– действительные числа.
Как видите, второй способ гораздо проще и рациональнее, но для подобных изысков, конечно, надо обладать некоторым опытом.
Надеюсь, данная статья окончательно развеяла все страхи перед векторами, и теперь вы с огромным удовольствием откроете учебник по линейной алгебре, чтобы изучить теорию векторных пространств, линейных преобразований и другие не менее интересные вещи.
Желаю успехов!
Решения и ответы:
Пример 2. Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
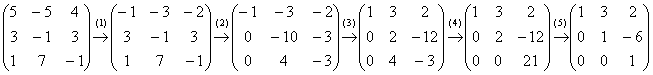 (1) К первой строке прибавили вторую строку, умноженную на –2.
(1) К первой строке прибавили вторую строку, умноженную на –2.
(2) Ко второй строке прибавили первую строку, умноженную на 3. К третьей строке прибавили первую строку.
(3) У первой строки сменили знак. Ко второй строке прибавили третью строку, умноженную на 3.
(4) К третьей строке прибавили вторую строку, умноженную на –2.
(5) Вторую строку разделили на 2, третью строку разделили на 21.
Ранг матрицы системы равен количеству переменных, значит, система имеет только тривиальное решение.
Ответ: ![]()
Пример 4. Решение: запишем матрицу системы и с помощью элементарных преобразований приведем её ступенчатому виду:
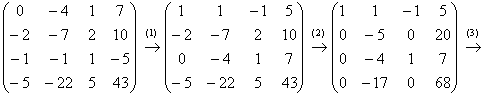
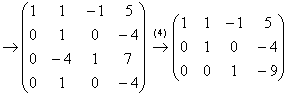
(1) У третьей строки сменили знак и переместили её на 1-е место.
(2) Ко 2-й и 4-й строкам прибавили первую строку, умноженную на 2 и 5 соответственно.
(3) Вторую строку разделили на –5, 4-ю строку разделили на –17.
(4) Вторая и 4-я строки одинаковы, последнюю строку удалили. К третьей строке прибавили вторую строку, умноженную на 4.
![]() – базисные переменные;
– базисные переменные;
![]() – свободная переменная.
– свободная переменная.
Выразим базисные переменные через свободную переменную.
Из последних двух уравнений:
![]() – подставим в первое уравнение:
– подставим в первое уравнение:
![]()
![]()
Таким образом, общее решение: ![]()
Найдем вектор фундаментальной системы решений. Для этого выберем в качестве значения свободной переменной ![]() :
:
![]()
Ответ: общее решение однородной системы уравнений:
![]() , где
, где ![]() (любое действительное число).
(любое действительное число).
Пример 6. Решение: запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
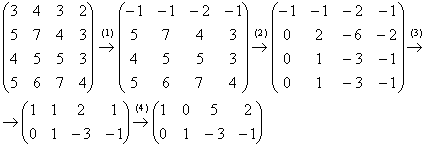
(1) К первой строке прибавили третью строку, умноженную на –1.
(2) Ко второй, третьей и четвертой строкам прибавили первую строку, умноженную на 5, 4 и 5 соответственно.
(3) Последние три строки пропорциональны, достаточно оставить только одну из них. У первой строки сменили знак.
(4) К первой строке прибавили вторую строку, умноженную на –1.
![]() – базисные переменные;
– базисные переменные;
![]() – свободные переменные.
– свободные переменные.
Выразим базисные переменные через свободные переменные:
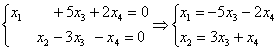
Таким образом, общее решение: ![]() .
.
Найдем векторы фундаментальной системы решений. Для этого последовательно выбираем в качестве значений свободных переменных следующие пары: ![]() и
и ![]() :
:
![]()
Ответ: общее решение: ![]() , где
, где ![]() – произвольные действительные числа.
– произвольные действительные числа.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright