Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

21. Проверка значимости коэффициента корреляции, коэффициентов
и уравнения линейной регрессии. Доверительные интервалы

На предыдущих уроках мы научились рассчитывать линейный коэффициент корреляции  и находить уравнение линейной регрессии . Однако не всё так просто. Дело в том, что эти результаты получены на основе выборочных данных (почти всегда) и возникает вопрос: а насколько достоверно они отражают реальную картину?

Ведь существует генеральная совокупность с генеральным линейным коэффициентом корреляции  («ро») и генеральным уравнением , и может статься, полученные по выборке значение  и уравнение  далеки от истины.

Ответить на этом вопрос нам помогут статистические гипотезы и доверительные интервалы. Сначала оглавление, затем примеры:

– Как проверить значимость выборочного линейного коэффициента корреляции?
– Как найти доверительный интервал для генерального коэффициента корреляции?
– Как проверить значимость коэффициентов уравнения линейной регрессии?
– Как найти доверительные интервалы для коэффициентов регрессии?
– Как проверить значимость выборочного уравнения линейной регрессии?
(значимость коэффициента детерминации)

  Да, и ещё видео есть (см. начало) по быстрому расчёту сего скарба в Экселе! Используйте для проверки подробного решения!

– Как найти доверительный интервал для точечного прогноза?

И сейчас мы быстренько разберёмся, что к чему. Опытные читатели могут сразу выбрать интересующий пункт, но я всё же рекомендую прочитать их по порядку, так как одно связано с другим:

Пример 71

По результатам Примера 67 найти всё перечисленное выше.

В той задаче нам была дана выборка из  студентов:
,
где  – количество прогулов студента (за некоторый период времени) и  – его суммарная успеваемость за этот период

По ходу решения мы получили выборочный коэффициент , что говорит о сильной обратной корреляционной зависимости успеваемости  от  количества прогулов . Кроме того, было найдено уравнение регрессии , которое показывает, что с увеличением количества прогулов на 1 единицу («икс») суммарная успеваемость падает в среднем на 6,0485  – примерно на 6 баллов.

Но насколько можно доверять полученным результатам?  Ведь перед нами выборка, причём, выборка малого объёма.

Решение, а точнее, небольшое исследование:

1) Проверим значимость выборочного коэффициента корреляции . Для этого рассмотрим нулевую гипотезу:

 – генеральный линейный коэффициент корреляции равен нулю, то есть успеваемость всех студентов не зависит от количества прогулов (линейно корреляционно).

Под словечком «всех» кроется изучаемая генеральная совокупность – можно рассмотреть студентов какого-то конкретного ВУЗа, либо студентов региона, либо студентов-приматов целой страны, либо вообще всех студентов на планете. Но здесь явно нет претензий на масштаб (выборка всего лишь 8 человек) – предположим, что исследуется успеваемость студентов вашего факультета.

В качестве альтернативной гипотезы стандартно рассматривают противоположное утверждение  – о том, что линейная корреляционная зависимость успеваемости от количества прогулов существует. При этом направление зависимости (прямая или обратная) не принимается во внимание, поскольку категоричному утверждению о равенстве нулю логично противопоставить и положительные значения . Ну а вдруг это факультет вундеркиндов, где прогулы только повышают успеваемость?

Заметьте заодно, что это один из немногих случаев, когда нулевая гипотеза является менее правдоподобной, нежели альтернативная.

Алгоритм проверки гипотезы работает по стандартному трафарету, который мы неоднократно использовали ранее. Сначала нужно задать уровень значимости, коль скоро он не предложен в условии. Возьмём традиционное значение .

Для проверки гипотезы  на уровне значимости  используем статистический критерий 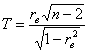, где  – объём выборки, а  – выборочный коэффициент корреляции. Напоминаю, что статистический критерий – есть величина случайная. Почему? В данном случае потому, что в разных выборках мы будем получать разные значения . Эта случайная величина имеет распределение Стьюдента с количеством степеней свободы , где «эм» – количество оцениваемых параметров. Здесь пациент один (коэффициент корреляции): , а посему .

Чтобы проверить нулевую гипотезу, нужно найти критическое значение   двусторонней критической области – для уровня значимости  и количества степеней свободы . В нашем случае  и:

 – это значение можно определить по таблице критических точек распределения Стьюдента (ориентируемся по верхней строке) либо с помощью соответствующей функции Экселя (пункт 10в).

! Примечание: во многих источниках используют понятие квантиля распределения, который рассчитывается для вероятности ,  но чтобы не разводить путаницу я буду придерживаться прежней схемы решения.

Теперь нужно вычислить наблюдаемое значение критерия . Если оно попадёт в область принятия гипотезы  (незаштрихованный участок на рисунке ниже), то на уровне значимости  нет оснований отвергать гипотезу . Если же   ( либо   – красный штрих), то нулевая гипотеза отвергается:

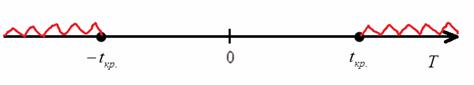
Проводим вычисления:
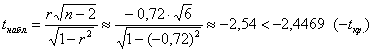, таким образом, на уровне значимости  гипотезу  отвергаем в пользу гипотезы .

Иными словами, выборочное значение  оказалось статически значимым и вряд ли объяснимо случайными факторами (малой выборкой, например).

При этом с вероятностью 0,05 мы совершили ошибку первого рода, то есть отвергли правильную гипотезу. Как видите, эта вероятность мала, а посему, уважаемые студенты, поменьше прогуливайте занятия, ибо статистическая проверка всего лишь по 8 студентам – и то – убедительно подтвердила падение успеваемости.

2) Теперь определим доверительный интервал для генерального линейного коэффициента корреляции .

Очевидно, что генеральный коэффициент  может быть как меньше, так и больше выборочного результата . И задача состоит в том, чтобы найти интервал , который с заранее заданной доверительной вероятностью (надёжностью)  накроет истинное значение генерального коэффициента :

Выберем популярное значение .

И тут развилка. Если выборка малА (ориентировочно ), то целесообразно использовать то же распределение Стьюдента с количеством степеней свободы . Это наш случай, и точность оценки в нём рассчитывается по формуле:

Для уровня доверительной вероятности  и количества степеней свободы  находим коэффициент доверия: , например, с помощью Расчётного макета (пункт 10б).

! Примечание: также можно использовать значение  и пункт 10в макета.

Таким образом:

и получается следующий интервал:

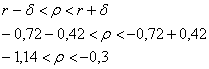
Поскольку коэффициент корреляции не может превосходить по модулю единицу, то левое значение корректируем:

 – итак, с вероятностью  данный интервал накрывает генеральный коэффициент корреляции .

Да, оценка весьма грубА, но, так или иначе, задание выполнено. И, как вы правильно догадались, виновником такого результата является слишком малый объём выборки. Это хорошо видно и по формуле:  – при увеличении  знаменатель растёт и, соответственно,  уменьшается.

Из формулы также нетрудно понять, что чем ближе выборочный коэффициент по модулю к единице, тем точнее будет оценка. Так, для  и того же значения  получается интервал , что уже очень и очень неплохо.

Интервал можно сузить, уменьшив доверительную вероятность , однако это неприемлемо для серьезного статистического исследования. Поэтому остаётся лишь увеличивать объём выборки, и случай  я разберу в следующей задаче. Там всё занятнее, но зато точнее.

3) Проверим значимость коэффициентов выборочного уравнения линейной регрессии . Иными словами, можно ли доверять значениям  или они далеки от соответствующих  коэффициентов генерального уравнения ?

Наиболее важным является коэффициент «а» при факторной переменной, с него и начнём. По исходным данным  (количество прогулов) и  (соответствующая суммарная успеваемость) заполним следующую расчётную таблицу:

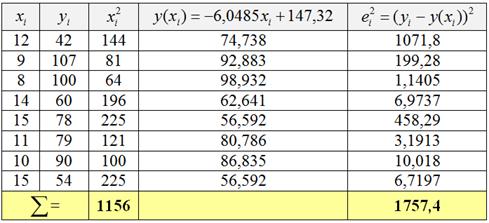
Примечание: если Пример 67 решён 1-м способом, то квадраты  и их сумма  уже найдены и в этом случае 3-й столбец не нужен. Он также не потребуется, если вам нужно проверить лишь коэффициент «а» (при факторной переменной «икс»).

В 4-м слева столбце с помощью выборочного уравнения регрессии  рассчитываем среднеожидаемую успеваемость студентов для эмпирических значений . Так, при количестве прогулов  среднеожидаемая успеваемость составит . И, наконец, в правом столбце находим квадраты  отклонений   эмпирических значений  успеваемости от соответствующих среднеожидаемых значений  , вычисленных по уравнению регрессии. Например: . О том, как быстро проводить подобные вычисления в Экселе, я неоднократно рассказывал ранее, посмотрИте хотя бы недавний ролик.

Теперь проверка, выберем тот же уровень значимости .   Рассмотрим нулевую гипотезу  – о том, что соответствующий коэффициент генерального уравнения  равен нулю. По сути это означает отсутствие линейной корреляционной зависимости между показателями.

И здесь тоже используется категоричная альтернатива  – гипотеза о том, что линейная корреляционная зависимость успеваемости от количества прогулов существует. Вновь обратите внимание, что направление гипотетической зависимости (прямая или обратная) не принимается во внимание, проверяется лишь тот факт – есть она или нет.

Для проверки гипотезы  на уровне значимости  используем статистический критерий , где  – выборочное значение коэффициента, а  – стандартная ошибка коэффициента «а». Случайная величина  имеет распределение Стьюдента с количеством степеней свободы , где  – количество оцениваемых параметров. Параметр у нас один (коэффициент «а»), поэтому .

Для уровня значимости  и количества степеней свободы  по соответствующей таблице либо с помощью Экселя (пункт 10в) находим критическое значение двусторонней области .

Если наблюдаемое значение критерия окажется в «красной» области ( либо ), то нулевая гипотеза отвергается в пользу альтернативной; если же , то оснований отвергать её на данном уровне значимости – нет.

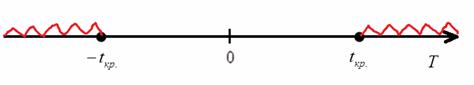
Наблюдаемое значение критерия найдём по формуле:

Выборочный коэффициент известен , а вот с его стандартной ошибкой придётся потрудиться:
, где  – среднее квадратическое отклонение признака-фактора (найдено в Примере 67), а «эс етое» – стандартная ошибка регрессии, которая отыскивается по формуле:
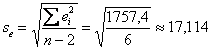  (сумма в числителе рассчитана в таблице выше).

В результате:
 и наблюдаемое значение критерия:

, таким образом, на уровне значимости  гипотезу  отвергаем в пользу гипотезы .

Иными словами, выборочное значение  оказалось статически значимым и вряд ли объяснимо случайными факторами, малой выборкой, например.

И внимательный читатель заметил, что здесь мы получили те же самые значения  и , что и в первом пункте! То есть, проверка значимости коэффициента при факторной переменной («икс») эквивалентна проверке значимости коэффициента корреляции. Что неудивительно, ведь оба коэффициента характеризуют линейную корреляционную зависимость, да вспОмните хотя бы формулу , в которой одно связано с другим.

Таким образом, если проверен один коэффициент, то фактически проверен и другой. Впрочем, в вашей задаче может требоваться и то и другое. И третье, и четвёртое, и пятое :)

Следует добавить, что в некоторых задачах в качестве нулевой гипотезы выдвигают , где  – ненулевое значение. В этом случае наблюдаемое значение критерия рассчитывается по формуле , а в остальном решение будет таким же.

Но это ещё не всё. Проверим значимость коэффициента . Давайте, кстати, посмотрим на уравнение  и вспомним смысл этого коэффициента: если студент не прогулял ни одного занятия , то  – есть в точности среднеожидаемая успеваемость такого монстра :)

В качестве нулевой гипотезы рассматриваем совсем уж невероятный случай  о равенстве нулю коэффициента генерального уравнения  (этакий факультет эльфов, которые посещают все занятия, но никто вообще ничего не понимает :)).

В качестве альтернативной гипотезы рассмотрим  – о том, что не все из них эльфы.

Решение будет «под кальку».  Для проверки гипотезы  на уровне значимости  используем статистический критерий , где  – выборочное значение коэффициента, а  – его стандартная ошибка. Эта случайная величина имеет то же  распределение Стьюдента с количеством степеней свободы , и для  уровня значимости  мы определили .

Знакомая картинка с областью отвержения (красный цвет) и областью принятия нулевой гипотезы:

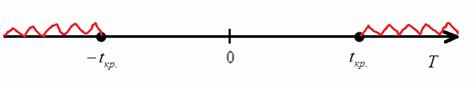
Вычислим стандартную ошибку коэффициента «бэ» (сумма квадратов найдена в таблице выше):
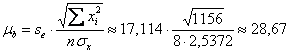, как вариант, её можно рассчитать через стандартную ошибку коэффициента «а»:
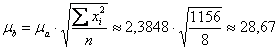, что несколько проще.

Вычислим наблюдаемое значение критерия:
, таким образом, на уровне значимости  гипотезу  отвергаем в пользу гипотезы .

То есть, выборочное значение  статически значимо отличается от нуля, что естественно.

В некоторых задачах рассматривают нулевую гипотезу , где , и тогда наблюдаемое значение критерия рассчитывается по формуле .

4) Найдём доверительные интервалы для генеральных коэффициентов  и . Это просто. Но оценка получится очень грубой, в частности потому, что выборка весьма малА.

Для первого коэффициента используем формулу:

Всё найдено в предыдущем пункте, осталось провести простецкие вычисления:

 – таким образом, с доверительной вероятностью   данный интервал накроет истинное значение генерального коэффициента .

И аналогичная формула для второго коэффициента:

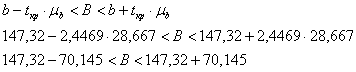
 – таким образом, с доверительной вероятностью   данный интервал накроет истинное значение генерального коэффициента

5) Проверим статистическую значимость всего выборочного уравнения  – можно ли с высокой степенью доверять этому результату или он далёк от генерального уравнения ? …Ну, после пунктов 1 и 3 доверять, очевидно, можно :) Но проблема состоит в том, что в разных задачах вам могут быть предложены разные пункты, и поэтому я разбираю каждый из них.

На самом деле поставленный вопрос эквивалентен вопросу о проверке значимости выборочного коэффициента детерминации , который мы, естественно, тоже рассчитали в Примере 67. «Естественно», потому что  – есть ключевой показатель. А именно, в рамках построенной линейной модели успеваемость на 51,74% зависит от количества прогулов. Оставшаяся часть вариации успеваемости (48,26%) обусловлена другими причинами, которые не учитываются уравнением . В статье об индексе детерминации и корреляции я подробно обосную вышесказанное, ну а пока возвращаемся к делам нашим практическим.

Поскольку , то проверка должна быть эквивалентна проверке значимости коэффициента корреляции (пункт 1). И это действительно так. Проверим гипотезу:

 – о том, что генеральный коэффициент детерминации равен нулю, иными словами количество прогулов вообще никак (на 0%) не влияет на успеваемость.

В качестве конкурирующей гипотезы рассмотрим логичное противопоставление  – о том, что такое влияние есть.

Для проверки гипотезы используем статистический критерий , где  – значение выборочного коэффициента детерминации (которое от исследования к исследованию случайно), а  – количество факторных (причинных) переменных. В нашей модели фактор один (успеваемость) , а посему критерий принимает вид . Эта случайная величина имеет распределение Фишера (-распределение) с количеством степеней свободы .

Для того же уровня значимости  и количества степеней свободы  по соответствующей таблице или с помощью расчётного макета (пункт 12) определяем критическое значение критерия:

Теперь вычислим наблюдаемое значение критерия. Если окажется что  (красный штрих) то гипотезу  на уровне значимости  отвергаем; если же , то отвергать её – оснований нет:

В нашей задаче:
, таким образом, на уровне значимости  гипотезу  отвергаем в пользу конкурирующей гипотезы .

Иными словами, выборочное значение  статистически значимо отлично от нуля, а значит, статистически значимо и выборочное уравнение .  Однако «статистически значимо» – это ещё не значит, что «отлично» или хотя бы «хорошо». Так, и оценки «троечника» ведь статистически значимо отличны от нуля :)

Вполне может статься, что зависимость близкА и к какой-нибудь нелинейной – если эмпирические точки располагаются примерно по параболе, гиперболе, экспоненте или вдоль какой-нибудь другой кривой. В этом случае мы получим низкое значение линейного коэффициента детерминации и его статическую незначимость, а значит, и незначимость всей линейной модели. То есть, линейная модель будет неудовлетворительно описывать ситуацию. Подбор оптимальной кривой и нелинейные модели…– уже на ваших экранах!

Возвращаясь к взаимосвязи коэффициентов  легко убедиться в том, что  – есть в точности критическое значение двусторонней области пункта 1, а  – есть в точности наблюдаемое значение того пункта.

Таким образом, для линейной однофакторной модели эквивалентными являются следующие проверки:

– проверка значимости коэффициента корреляции;
– проверка значимости коэффициента факторной переменной уравнения регрессии;
– проверка значимость коэффициента детерминации.

И если проверено что-то одно, то по существу, проверено и второе и третье. Но, повторюсь, в вашей задаче вас могут заставить «пропахать» все три пункта.

И в заключение параграфа хочу добавить, что рассмотренный критерий Фишера работает и в многофакторных линейных моделях. ...Я, наконец, добрался до двухфакторной модели :) …на 13-й год развития сайта.

И на десерт:

6) Точечный прогноз и доверительный интервал прогноза.

Для чего нужно полученное уравнение ? Ну, конечно же, хочется что-нибудь спрогнозировать. Оценим суммарную успеваемость   при  прогулах:
 баллов.

Но это лишь точечный прогноз, вычисленный к тому же по выборочному уравнению. А ведь существует генеральное уравнение регрессии  и, следовательно, генеральное прогнозируемое значение успеваемости  при . И наша задача состоит в том, чтобы найти доверительный интервал:

  – который с заранее заданной доверительной вероятностью  (например) накроет истинное значение .

Используем формулу , где  – коэффициент доверия, а  – стандартная ошибка точечного прогноза.

Для уровня доверительной вероятности  и количества степеней свободы  находим коэффициент доверия  (Макет, пункт 10б).

Стандартную ошибку точечного прогноза вычислим по формуле:
, где  – стандартная ошибка регрессии (вычислена в пункте 3),  – выборочное среднее значение признака-фактора (вычислено в ходе решения Примера 67),  (вычислена там же, 2-й способ решения).

АККУРАТНО подставляем все значения и ВНИМАТЕЛЬНО считаем:

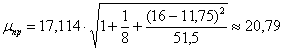
Таким образом,  и искомый доверительный интервал:

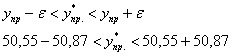
левое значение естественно округлим до нуля:
 – данный интервал с вероятностью  накрывает истинное генеральное значение  прогноза успеваемости при  прогулах.

И оценка, конечно, опять получилась грубой, надежда, короче, для прогульщиков :) Но статистика, она неумолима – повезло раз, повезло два и может даже три, а потом….
Иными словами, при увеличении объема выборки наступает неизбежная закономерность.

И я рад, что вы читаете эти строки! Это нужно отметить. Аналогичной задачей, в которой исходные данные сведены в комбинационную таблицу:

Пример 72

По результатам Примера 69 на уровне значимости :

– проверить значимость выборочного линейного коэффициента корреляции;
– найти доверительный интервал для генерального коэффициента корреляции;
– проверить значимость коэффициентов уравнения линейной регрессии;
– найти доверительные интервалы для коэффициентов регрессии;
– проверить значимость выборочного уравнения линейной регрессии;
– найти доверительный интервал для прогнозного значения признака-результата, который соответствует .

В подобных ситуациях я традиционно предлагаю решить задачу самостоятельно, но здесь будет много новых моментов, а посему решаю сам. Итак, в Примере 69 по 40 предприятиям региона:

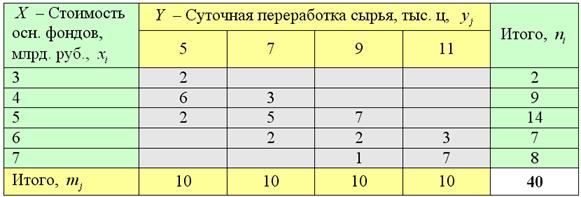
нами была установлена  – сильная прямая линейная корреляционная зависимость суточной переработки сырья от стоимости основных фондов, а также найдено выборочное уравнение регрессии , которое показывает, что  при увеличении стоимости основных фондов на 1 млрд. руб. суточная переработка сырья увеличивается в среднем на 1,61 тысяч центнеров.

…Все вникли в условие? Ещё раз перечитайте входные данные… Отлично! – поехали:

1) Проверим значимость выборочного коэффициента корреляции , а именно, рассмотрим гипотезу   против конкурирующей гипотезы  . Нулевая гипотеза говорит нам о том, что генеральный коэффициент корреляции (который, в принципе, можно рассчитать по ВСЕМ предприятиям региона), равен нулю, то есть линейная корреляционная зависимость отсутствует. И альтернатива утверждает, что эта зависимость (переработки сырья от стоимости фондов) существует.

Для проверки гипотезы  на уровне значимости  используем статистический критерий 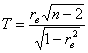, где  – объём выборки, а  – выборочный коэффициент корреляции

Для уровня значимости  и количества степеней свободы  с помощью соответствующей функции Экселя (пункт 10в) определяем критическое значение двусторонней области:

Если окажется, что наблюдаемое значение критерия попадает в интервал , то оснований отвергать нулевую гипотезу – нет:

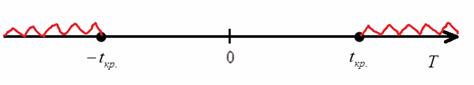
Проводим вычисления:
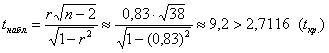, таким образом, на уровне значимости  гипотезу  отвергаем в пользу гипотезы .

Иными словами, выборочное значение  статически значимо и вряд ли объяснимо случайными факторами, при этом с вероятностью 0,01 мы совершили ошибку первого рода, то есть отвергли правильную гипотезу (когда линейной зависимости на самом деле нет, но мы это отвергли).

2) Определим доверительный интервал для генерального линейного коэффициента корреляции . Поскольку выборка достаточно велика , то целесообразно использовать так называемое преобразование Фишера. Не вдаваясь в его содержательную суть, приведу формальный технический алгоритм.

Преобразуем выборочный коэффициент корреляции по формуле:
, это значение можно подсчитать на калькуляторе либо с помощью специальной функции Экселя (да, разработчики позаботились): =ФИШЕР(r).

Вычислим стандартную ошибку коэффициента «зет»:

Для уровня доверительной вероятности   из соотношения  найдем коэффициент доверия :
 – определяем с помощью таблицы значений функции Лапласа либо по Макету (пункт 5*).

Вычислим нижнюю границу доверительного интервала:

и его верхнюю границу:

Теперь нужно вернуться в размерность нашей задачи с помощью обратного преобразования Фишера:

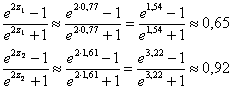
В Экселе эти значения легко рассчитать с помощью функции =ФИШЕРОБР( ) – для нижнего конца  и для верхнего конца .

Таким образом, искомый доверительный интервал:

 – с вероятностью  накрывает генеральный коэффициент корреляции .

Следует заметить, что интервал получился довольно широким – по той причине, что мы задали суровую надёжность. Если её уменьшить, например, до , то получится более симпатичный результат: .

Рассмотренный метод хорошо работает, если выборка достаточно великА (20-30 наблюдений, по крайне мере) и коэффициент корреляции близок по модулю к единице.

3) Проверим статистическую значимость коэффициентов выборочного уравнения . Проверка будет трафаретной, но с некоторыми техническими новинками и хитростями.

Сначала коэффициент при факторной («иксовой» переменной) . Выдвигаем нулевую гипотезу  о том, что соответствующий  коэффициент генерального уравнения  равен нулю (т.е. линейной корреляционной зависимости не существует). В качестве конкурирующей гипотезы рассматриваем противоположное утверждение .

Чтобы проверить гипотезу  на уровне значимости  используем тот же критерий , где  – выборочное значение коэффициента, а  – его стандартная ошибка.

Для уровня значимости  и количества степеней свободы  с помощью соответствующей функции Экселя (пункт 10в) находим критическое значение двусторонней области .

Не поленюсь, для наглядности снова скопирую рисунок с областью отвержения (красный цвет) и областью принятия нулевой гипотезы:

Наблюдаемое значение критерия найдём по формуле . И здесь вместо того, чтобы выполнять кропотливые вычисления по аналогии с предыдущей задачей, выгоднее использовать тот факт, что проверка значимости коэффициента корреляции равносильна проверке коэффициента при факторной переменной.

Вычислим стандартную ошибку коэффициента «а»:

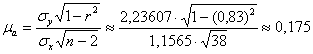
и наблюдаемое значение:
, поэтому на уровне значимости  гипотезу  отвергаем в пользу гипотезы .
Примечание: поскольку , то фактически мы провели те же вычисления, что и в первом пункте.

Вывод: коэффициент  статистически значим.

Для проверки значимости коэффициента  выдвигаем гипотезу  о равенстве нулю соответствующего коэффициента генерального уравнения . Конкурирующая гипотеза стандартна:

Критерий аналогичен: , где  – выборочное значение коэффициента, а  – стандартная ошибка этого коэффициента.

Уровню значимости  и количеству степеней свободы  соответствует то же значение  и те же области:

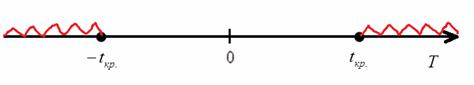
Стандартную ошибку коэффициента «бэ» рассчитаем через стандартную ошибку коэффициента «а»:
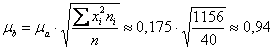  (сумма  найдена в Примере 69)

Вычислим наблюдаемое значение критерия:
 – данное значение попало в область принятия гипотезы , поэтому на уровне значимости  нет оснований отвергать гипотезу .

Вывод: коэффициент  статистически не значим и его отличное от нуля значение, вероятнее всего, обусловлено статистической погрешностью выборки.

Таким образом, генеральное уравнение регрессии с высокой вероятностью имеет вид  и самый что ни на есть реалистичный смысл: если стоимость фондов равна нулю , то суточная переработка сырья тоже нулевая.…Хотя, может статься, при нулевой балансовой стоимости сырьё начинают потихоньку разворовывать, и отрицательное значение  вовсе не случайно :) Кроме шуток, следует заметить, что на каких-то предприятиях это может и так, но статистическая проверка показала, что данный факт не характерен для всей генеральной совокупности.

4) Найдём доверительные интервалы для генеральных коэффициентов  и .

Для коэффициента при факторной переменной:

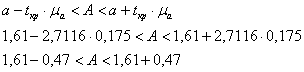
 – данный интервал с доверительной вероятностью  накрывает истинное значение генерального коэффициента .

Обратите внимание, что интервальная оценка получилась гораздо более качественной, нежели в предыдущем примере – вот что значит бОльший объём выборки. Но интервал, конечно, всё равно широк.

И доверительный интервал для свободного члена:

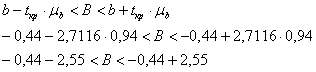
 – данный интервал с вероятностью   накрывает истинное значение генерального коэффициента

Да, оценка тривиальна, но примечательно, что ноль вошёл в эту область, и интервал получился почти симметричным относительно нуля.

5) Проверим статистическую значимость всего выборочного уравнения , а значит, выборочного коэффициента детерминации .

Напоминаю, что эта проверка эквивалентна проверкам пунктов 1 и 3, и её технический алгоритм ничем не отличается от предыдущей задачи.

Проверим гипотезу  – о том, что генеральный коэффициент детерминации равен нулю, то есть,  стоимость основных фондов вообще никак (на 0%) не влияет на суточную переработку сырья. И естественная альтернатива  , состоящая в том, что такое влияние есть.

Для проверки гипотезы используем случайную величину (статистический критерий) , которая имеет распределение Фишера (-распределение) с количеством степеней свободы .

Для уровня значимости  и количества степеней свободы  с помощью соответствующей функции Экселя (пункт 12) определяем критическое значение критерия:

Если окажется, что наблюдаемое значение критерия  (красный цвет), то гипотезу  на уровне значимости  отвергаем, если , то отвергать её – оснований нет:

В нашем случае:
, таким образом, на уровне значимости  гипотезу  отвергаем в пользу конкурирующей гипотезы .

Вывод: выборочное уравнение  и коэффициент детерминации  статически значимы. Линейная корреляционная модель подобрана удачно (для описания зависимости суточной переработки сырья от стоимости основных фондов).

6) С помощью выборочного уравнения получим точечный прогноз суточной переработки сырья при стоимости основных фондов в  млрд. руб.:

 тыс. ц.

Определим доверительный интервал  , который с доверительной вероятностью   накроет истинное прогнозное значение , полученное с помощью генерального уравнения . И, как мы выяснили, кстати, свободный член этого уравнения, с точки зрения статистики, равен нулю .

Используем формулу , где  – коэффициент доверия, а  – стандартная ошибка точечного прогноза.

И этот коэффициент доверия нам уже хорошо известен из предыдущих пунктов:  – для доверительной вероятности  и количества степеней свободы .

Стандартную ошибку точечного прогноза вычислим по формуле:
, и здесь её нужно немного видоизменить.

Стандартную ошибку регрессии выразим из формулы  предыдущей задачи: ,  а сумму в знаменателе – из формулы для вычисления дисперсии :

, откуда следует:

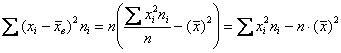
И главное тут ничего не напутать, сейчас вычислю это на калькуляторе, затем перепроверю в Экселе:

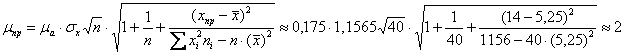
Таким образом,  и искомый доверительный интервал:

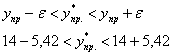
– данный интервал с вероятностью  накрывает истинное генеральное прогнозное значение  суточной переработки сырья при стоимости основных фондов в  млрд. руб.

Готово, молодцы!

И я жду вас на следующем уроке, где мы подробно разберём математическую суть регрессионной модели.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте