Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Гипергеометрическое распределение вероятностей

Пожалуй, второе по распространённости после биномиального распределения, в котором нет ничего гиперсложного. Да и сложного тоже. С гипергеометрическим законом распределения вероятностей мы неоднократно сталкивались ранее и фактически полностью построили в Примере 12 урока о классическом определении вероятности. Сформулируем задачу в общем виде и вспомним этот пример:

Пусть в совокупности из  объектов содержатся  объектов, обладающие некоторым признаком. Из этой совокупности случайным образом и без возвращения извлекается  объектов. Тогда случайная величина  – количество «особых» объектов в выборке – распределена по гипергеометрическому закону.

В ящике находится  деталей, среди которых  бракованных. Наудачу извлекаются  детали. Найти вероятность того, что:
а) обе детали будут качественными;
б) одна деталь будет качественной, а одна – бракованной;
в) обе детали бракованны

По сути дела, здесь фигурирует случайная величина  – количество бракованных деталей в выборке. Прорешаем данную задачу под другим углом зрения, а именно, найдём закон распределения этой случайной величины, которая, очевидно, может принять одно из следующих значений: . Соответствующие вероятности  определяются правилами и формулами комбинаторики и классическим определением вероятности.

Сначала вычислим количество всех возможных наборов из 2 деталей. Две детали можно выбрать  способами. Дальнейшие действия удобно занумеровать:

0)  (в выборке нет бракованных деталей)
 способами можно извлечь 2 качественные детали.
По классическому определению:  – вероятность того, среди 2 извлечённых деталей не будет бракованных.

1)
 способами можно извлечь 1 качественную деталь и 1 бракованную.
По тому же определению:  – вероятность того, среди 2 извлечённых деталей будет 1 бракованная.

2) И, наконец,
 способами можно извлечь 2 бракованные детали.
 – вероятность того, что обе извлечённые детали будут бракованными.

Таким образом, закон распределения количества бракованных деталей в выборке:

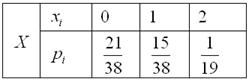
Контроль:

Следует отметить, что «зеркальная» случайная величина  – количество качественных деталей в выборке, тоже имеет гипергеометрическое распределение. Догадайтесь с одного раза, как выглядит её закон распределения. НО, к этому вопросу нельзя подходить формально! Самостоятельно разберите такую ситуацию:

Задание

Из ящика с 19 стандартными и 1 нестандартной деталью, наудачу извлекается 2 детали. Составить закон распределения случайной величины  – количества стандартных деталей в выборке.

Решение и ответ в конце урока.

…Разминка прошла успешно? Отлично! Теперь разберём более содержательную задачу, в которой я расскажу вам об общих формулах и полезных технических приёмах решения. Как в передаче «Что? Где? Когда?» выносят чёрные ящики, так в теории вероятностей предлагают урны с шарами :)

Задача

Из урны, содержащей 6 белых и 4 черных шара, случайным образом и без возвращения извлекают 3 шара.

! Примечание: оговорка «без возвращения» является важной, но её часто опускают, подразумевая этот факт по умолчанию

Составить закон распределения случайной величины  – числа черных шаров среди взятых. Найти математическое ожидание и дисперсию этой случайной величины. Построить многоугольник и функцию распределению. Вычислить вероятность того, что в выборке будет не менее двух чёрных шаров. Вычислить .

Как говорится, весь джентльменский набор. Кстати, если не нравятся шары, можете представить, что это белые и чёрные котята или…, не знаю, например, красные и чёрные карты.

Решение: поскольку в условии речь идёт о выборке объектов из совокупности и о количестве «особенных» объектов в этой выборке, то предложенная случайная величина имеет гипергеометрическое распределение вероятностей. Составим её закон распределения.

Обозначим исходные данные стандартными буквами:

 – размер совокупности;
  – количество черных шаров в совокупности («особенный» признак);
 размер выборки.

Очевидно, что случайная величина  (кол-во чёрных шаров в выборке)  принимает следующие значения:

Следует заметить, что этих значений может быть и меньше. В каких случаях? В случае если , то есть, если во всей совокупности чёрных шаров МЕНЬШЕ, чем размер выборки. Так, например, если в урне всего 2 чёрных шара, то значение  отпадёт. И противоположная ситуация – когда в урне недостаточно белых шаров (меньше размера выборки), так, если там 9 чёрных и 1 белый шар, то в выборке обязательно окажутся хотя бы два чёрных шара, т. е. отпадают значения , .

Для вычисления гипергеометрических вероятностей существует формула , но я вам крайне советую вникать в смысл выполняемых действий. Сначала вычислим знаменатель дроби:
 способами можно выбрать 3 шара из 10. Данное значение нам потребуется при вычислении каждой вероятности :

0)  (в выборке нет чёрных шаров)
 способами можно выбрать 0 чёрных и 3 белых шара.
По классическому определению:
 – вероятность того, что в выборке будет 0 черных шаров.

Результаты лучше записывать в трёх видах: несокращённой обыкновенной дробью, сокращённой обыкновенной дробью и десятичной дробью (с 3-4-5 знаками после запятой). Это упростит решение, и скоро будет понятно, как.

Кроме того, вероятности выгодно знать заранее. Для этого можно использовать экселевскую функцию =ГИПЕРГЕОМЕТ(x; n; M; N) или сразу воспользоваться готовым расчётным макетом (Пункт 8).

Едем дальше:

1)
 способами можно выбрать 1 чёрный и 2 белых шара.
 – вероятность того, что в выборке окажется 1 чёрный шар.

2)
 способами можно выбрать 2 чёрных и 1 белый шар.
 – вероятность того, что в выборке окажется 2 чёрных шара.

3)
 способами можно выбрать 3 чёрных и 0 белых шаров.
 – вероятность того, что в выборке будет 3 чёрных шара.

Таким образом, количество чёрных шаров в выборке распределено по следующему закону:

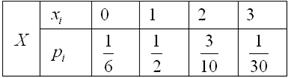
Вероятности по возможности записываем обыкновенными дробями!

Контроль: , ч.т.п.

В крайнем случае можно использовать десятичные дроби (когда обыкновенные сильно наворочены), единственное, нужно следить, чтобы сумма округлённых значений равнялась единице и при необходимости «подгонять» некоторые вероятности. Однако помните, что это уже будет не точным ответом!

Но десятичные значения, безусловно, удобны для построения многоугольника распределения:

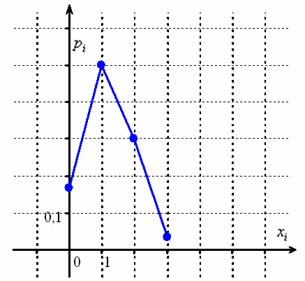
Математическое ожидание и дисперсию гипергеометрического распределения можно вычислить в обход общего алгоритма – по специальным формулам:

 – среднее количество чёрных шаров в выборке (при многократном повторении таких выборок).

 – мера рассеяния количества чёрных шаров относительно матожидания.

Составим функцию распределения вероятностей. И здесь как раз пригодятся несокращённые обыкновенные дроби. Вычислим накопленные частоты:

 – десятичные значения нужны для ручного построения графика.

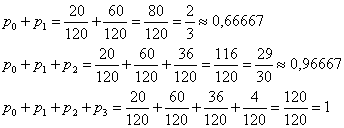
Таким образом, искомая функция:

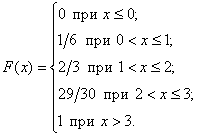
– её значения тоже записываем обыкновенными дробями! Дабы соблюсти точность.

Строим график:

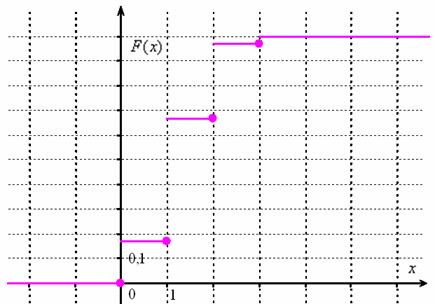
Выходим на финишную прямую. Вычислим  – вероятность того, что в выборке будет не менее двух чёрных шаров. Это можно сделать не единственным способом. Прямым суммированием вероятностей несовместных исходов:

или с помощью функции распределения и штатной формулы :

Напомню, что здесь существуют критично важные тонкости (см. по ссылке выше).

И, наконец, рассчитываем стандартную вероятность  того, что значение случайной величины  отклонится от математического ожидания не более чем на одно среднее квадратическое отклонение:

Готово.

Основная трудность гг-распределений состоит в технике вычислений – в них нужно грамотно управляться с дробями, которые частенько получаются страшноватыми. Ну, и конечно, не забываем о том, КАКАЯ ИМЕННО дана случайная величина. Так, в разобранном задании может быть предложено  – количество белых шаров в выборке, и тогда решение примет «зеркальный» характер.

Дополнительные примеры по теме можно найти в pdf-сборнике, и я поздравляют вас с освоением основных дискретных распределений. Но, само собой, существуют и другие их виды, которые не вошли в этот курс.

Далее по фарватеру непрерывная случайная величина.

Нескучного чтения!

Решение и ответ на задание:

 способами можно извлечь две детали.
Случайная величина  может принять одно из следующих значений: .
Примечание: значение  невозможно, т.к. в ящике только 1 нестандартная деталь.
Составим закон распределения этой случайной величины:
1)
 способами можно извлечь 1 стандартную и 1 нестандартную деталь.
По классическому определению:
2)
 способами можно извлечь 2 стандартные детали.

Контроль:

Ответ: закон распределения количества стандартных деталей в данной выборке:

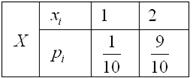
Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте