Линейные преобразования для «чайников»

На двух ближайших уроках я вкратце расскажу вам ещё об одном разделе высшей алгебры, который касается линейных преобразований… и тут сразу, заметьте, напрашивается добавить «преобразований чего-то». Тема обширная, тема интересная, и моя скромная задача состоит в том, чтобы в доступной форме донести до читателя её основы. В этой связи статья будет посвящена не только абстрактным алгебраическим вопросам, но и наполнена богатым геометрическим содержанием. Кроме того, сегодня мы обобщим такое важное понятие как вектор, имеющий к сему содержанию лишь частное отношение.

Есть ли среди вас начинающие изучать высшую математику? …хотя, чего тут спрашивать, конечно же, есть… – не смогли ведь пройти мимо заголовка! …Ну вот вы мне и попались, голубчики =) Для эффективного изучения материала нужно знать основы алгебры, аналитической геометрии, а также уметь выполнять действия с матрицами. На самом деле всё довольно просто, но если у вас возникнут вопросы (или уже встретился какой-то непонятный термин), то, пожалуйста, воспользуйтесь ссылками.

Обобщение понятия вектора. Векторное пространство

Ожидание казни хуже самой казни и поэтому лучше сразу почувствовать леденящий холодок настоящей алгебры =) Начнём с обещанного разбора полётов, а именно с понятия вектора. Давайте вспомним, что мы о нём знаем. Палочка со стрелочкой, знакомая ещё из школы. В высшей математике эта палочка «поднялась» до свободного вектора плоскости и пространства. Хорошо…. Далее слово «вектор» встретилось нам в ходе изучения матриц. Так, например, матрицу «один на два» мы называем вектором-строкой, а матрицу «три на один» – вектором-столбцом. Это векторы? Да, это векторы! Причём эти векторы сами по себе не имеют никакого отношения к геометрии. В своих статьях по алгебре я неоднократно оговаривался, что «данный вектор нужно понимать в алгебраическом смысле» и на уроке о ранге матрицы привёл краткую теоретическую справку по этому поводу: вектор – это упорядоченный набор чисел (обычно действительных)… и далее по тексту. А вот это уже более близко к истине: здесь, скажем, двумерный вектор понимается именно как упорядоченная пара чисел, которую, в частности можно интерпретировать, как координаты геометрического вектора. Или как решение системы линейных уравнений (см., например, статью об однородных системах). Или ещё как-нибудь.

Но и это частность! На самом деле в определённом контексте векторами являются матрицы, многочлены, функции и т.д. …и даже наши «обычные» действительные числа! А почему нет? Пожалуйста: множество векторов (никаких геометрических ассоциаций!), имеющих в наборе одно действительное число .

Так что же такое вектор? Что объединяет все эти случаи?

Предположим, что для всех элементов некоторого множества определены операции их сложения и умножения на скаляр , причём результаты этих операций (полученные элементы) тоже принадлежат данному множеству. Если при этом выполнены следующие восемь аксиом (см. по ссылке), то рассматриваемые элементы называются векторами (никаких ассоциаций!!), а всё их множество – векторным или линейным пространством

Обратите внимание на обозначения: абстрактный вектор чаще всего записывают жирной буквой – чтобы не возникало путаницы с различными «конкретными» векторами. Для векторного пространства стандартно используется буква .

Итак, какие бы «частные семейства» векторов мы ни взяли (геометрические, матричные, строковые и т.д.) – для каждой из этих алгебраических структур справедливо следующее:

– все элементы рассматриваемого множества можно складывать и умножать на скаляр (далее работаем с действительными числами), причём результаты этих операций тоже принадлежат данному множеству.

– для операций сложения и умножения выполнены аксиомы векторного пространства.

И здесь следует отметить, что термины «сложение» и «умножение» тоже носят общий символический смысл – в зависимости от природы того или иного векторного пространства эти операции определяются по-разному.

В курсе линейной алгебры проводится скрупулезная проверка различных множеств на предмет того, образуют ли они линейное пространство. И если удастся определить сложение и умножение на скаляр медведей на велосипеде и доказать для данных операций выполнение указанных 8 аксиом, то векторами будут и эти объекты =)

А теперь к основной теме урока:

Что такое линейное преобразование?

Если в линейном пространстве каждому вектору по некоторому правилу поставлен в соответствие вектор этого же пространства, то говорят, что в данном пространстве задана векторная функция векторного аргумента: (во избежание разночтений с другими математическими записями скобки нередко опускают: ).

Данная функция называется линейным преобразованием, если для неё выполнены пресловутые свойства линейности, с которыми вы ещё не раз столкнётесь в ходе изучения высшей математики:

,
, где – произвольные векторы данного пространства, а – действительное число.

Линейное преобразование также называют линейным оператором.

Следующий пример оброс не только бородой, но и волосами на спине: рассмотрим линейное пространство векторов-строк вида , в котором определены операция сложения и умножения вектора на число .

Никакой геометрии!!! – то, что я сформулировал в статье о ранге матрицы, называется
-мерным арифметическим векторным пространством, и сейчас мы имеем дело с частным арифметическим пространством размерности 2.

Докажем, что функция векторного аргумента является линейным преобразованием. Доказательство состоит в проверке свойств линейности:

Здесь мы воспользовались дистрибутивностью умножения на скаляр относительно сложения векторов (одна из аксиом векторного пространства)

А здесь – аксиомой ассоциативности умножения на скаляр, коммутативностью (перестановочностью) самих действительных чисел (аксиома поля) и снова той же аксиомой ассоциативности.

Читателям, которым предстоит изучать теорию высшей алгебры, следует привыкнуть к таким доказательствам. Беспощадно формально, но, как сказали бы древние римляне, Dura algebra sed algebra =)

Таким образом, – это линейное преобразование.

Разумеется, далеко не всякий оператор является линейным, и в других источниках информации можно найти массу примеров, как на удачную, так и неудачную проверку различных преобразований на линейность. И со строгостью доказательств на практике обычно всё попроще, …хотя, тут от преподавателя зависит – и по-хорошему, в математике ещё нужно обосновать, почему «ноль не равен единице».

Ну а сейчас мы спускаемся на землю грешную и переходим к геометрическому смыслу линейных преобразований. Пусть – это множество геометрических векторов плоскости. Для простоты рассмотрим привычный ортонормированный базис и прямоугольную систему координат .

Если задан какой-либо базис, то линейное преобразование удобнее представить в матричном виде. Как записать оператор в виде матрицы? На этот счёт существует общее правило: чтобы записать матрицу линейного преобразования в -мерном базисе нужно последовательно и строго по порядку применять данный оператор к базисным векторам, а результаты заносить в столбцы матрицы (слева направо).

Наш случай элементарен: сначала применим линейное преобразование к первому базисному вектору: и запишем результат в 1-й столбец: . Затем «обрабатываем» 2-й орт: и заносим полученные координаты во 2-й столбец:

– матрица линейного преобразования в базисе .

Протестируем построенную матрицу с помощью вектора . Для этого «уложим» его координаты в вектор-столбец и выполним следующее матричное умножение:
– в результате «на выходе» получены координаты вектора , что и требовалось проверить.

Поскольку любая точка плоскости однозначно определяется её радиус-вектором ( – начало координат), то матрица преобразования, по существу, применима и к координатам точек. И далее для простоты я буду говорить, что, например, точка :
– перешла в точку .

Наверное, все уже поняли, что делает этот оператор. Мысленно представьте произвольный треугольник на плоскости. После применения рассматриваемого линейного преобразования данный треугольник увеличится в два раза. Такие треугольники (имеющие равные соответствующие углы), как многие помнят из школы, называются подобными. Да и сам оператор носит такое же название:

Линейное преобразование называется преобразованием подобия или гомотетией, причём:

– если , то речь идёт об однородном растяжении (увеличении) объектов плоскости в раз;
– если – то о сжатии (уменьшении) в раз;
– если , то преобразование тождественно (ничего не меняет).

И если меньше нуля, то дополнительно к растяжению / сжатию / неизменности векторы меняют направление, а точки отображаются симметрично относительно начала координат.

При имеет место так называемое нулевое преобразование.

Следует отметить, что на прикладном и «любительском» уровне линейные преобразования чаще всего как раз и ассоциируются именно с геометрическими преобразованиями. Рассмотрим ещё несколько популярных примеров по теме, и, чтобы разнообразить серые геометрические будни, мысленно нарисуем на координатной плоскости кошачью морду. Можно и не мысленно =)

…Представили? Нарисовали? Отлично!

Преобразование растягивает объекты плоскости по направлению вектора (горизонтали) в 2 раза, после чего кот Леопольд радует нас своей широкой-широкой улыбкой!

…хотя у многих, наверное, не кот… да и не факт, что с улыбкой… – как говорится, у каждого в голове своя морда =)

И в самом деле, преобразуем точку :
– «иксовая» координата увеличилась в 2 раза, а «игрековая» – не изменилась.

Преобразование сожмёт кота по горизонтали в 3 раза. Желающие могут по ходу объяснений ~~приготовить мясорубку~~ тестировать для рассматриваемых матриц различные векторы и точки. Читателям с маломальскими навыками матричного умножения не составит особого труда делать это устно.

Преобразование вытянет все ненулевые объекты плоскости по направлению вектора (по вертикали) в полтора раза. Это будет очень удивлённый кот....

Дополнительные знаки «минус» приведут к зеркальному отображению объектов (относительно оси ординат либо начала координат).

– образно говоря, «челюсть налево, лоб направо». Это преобразование называется перекосом или сдвигом плоскости в направлении вектора (в данном случае).

– данное преобразование поворачивает векторы системы против часовой стрелки на угол .

И, наконец, венчает все эти метаморфозы ещё один лохматый пример:
преобразование переводит единичный квадрат с вершинами в параллелограмм с вершинами .

А тут уж дело случая – может получиться, как комната смеха, так и комната страха – зависит от того или иного преобразования.

Из вышесказанного нетрудно понять, что в базисе любой квадратной матрице «два на два» соответствует некоторое линейное преобразование, и наоборот любому линейному преобразованию соответствует своя матрица «два на два». И данный факт справедлив вообще для любого аффинного базиса , причём одно и то же линейное преобразование в разных базисах будет иметь в общем случае разные матрицы (что следует из самого принципа формирования этих матриц).

По аналогичной схеме можно рассмотреть векторы нашего трёхмерного пространства, с тем отличием, что преобразований будет больше, преобразования будут веселее. И, разумеется, линейные преобразования «работают» в векторных пространствах бОльшей размерности, однако там они уже далеки от геометрии.

Разминаемся:

Пример 1

В некотором аффинном базисе задано линейное преобразование . Найти образ точки . Используя обратное преобразование, выполнить проверку.

Решение: потихоньку нагружаю вас терминологией: образ – это то, что должно получиться в результате преобразования. В данном случае, очевидно, должна получиться некоторая точка . Исходная точка , соответственно, является прообразом.

! Надеюсь, все понимают, что штрихи в данном контексте не имеют никакого отношения к производным.

Образы векторов и точек мы уже неоднократно находили выше:

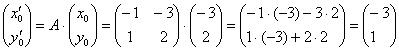
Таким образом, линейное преобразование перевело точку в точку .

Теперь найдём матрицу обратного преобразования, которое превращает образы векторов и точек обратно в их прообразы. Для этого запишем простейшее матричное уравнение (где – координатный столбец прообразов, а – образов) и для его разрешения относительно умножим обе части на обратную матрицу слева:

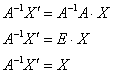
«Развернём» уравнение в привычном порядке:

Обратную матрицу можно найти через алгебраические дополнения либо методом Гаусса-Жордана, но здесь я рекомендую первый способ, поскольку он позволит быстро выяснить, а существует ли матрица вообще.

Заряжаем стандартный алгоритм. Сначала вычислим определитель:
, значит, матрица линейного преобразования обратима. С содержательной точки зрения это означает, что обратное линейное преобразование существует и задаётся оно в точности матрицей .

Здесь и далее я не буду подробно расписывать процесс нахождения обратной матрицы. Итак, в результате стандартных действий находим и выясняем, во что превратится найденная точка :

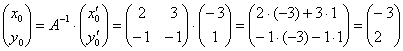– получены координаты исходной точки , что и требовалось проверить.

Ответ:

Следует отметить, что обратное преобразование осуществимо далеко не всегда. Так бывает, например, при проектировании векторов на координатные оси или при тривиальном нулевом преобразовании. В таких случаях определитель матрицы прямого оператора равен нулю и обратной матрицы не существует.

Творческая задача для самостоятельного решения:

Пример 2

В результате применения оператора в некотором базисе получены образы . Найти прообразы данных векторов.

Краткое решение и ответ в конце урока. Обратите внимание, что формулировка данной задачи вовсе не утверждает, что речь идёт именно о геометрических векторах. Как оно, собственно, и бывает в большинстве типовых заданий, которые для полного комфорта оформляются малопонятной клинописью:

Пример 3

Даны два линейных преобразования:

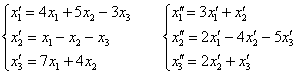
Спокойно, спокойно, сейчас во всём разберёмся…

Средствами матричного исчисления найти преобразование, выражающее через .

Решение: и как раз первое, что здесь можно сказать – это отсутствие информации о характере векторов 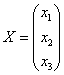. Известно только, что они заданы в некотором базисе, ибо матрица линейного преобразования НЕ МОЖЕТ существовать без базиса (т.к. она порождается базисными векторами). Сам базис нам тоже не известен, но для решения задачи информация о нём и не нужна.

Тем не менее, для пущего понимания предположим, что все дела происходят в обычной декартовой системе координат . И, чтобы не прослыть живодёром, я рассмотрю 3D-модель кота Леопольда =)

Запишем матрицу левого преобразования: 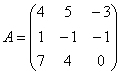. Данное преобразование переводит векторы 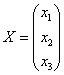в образы 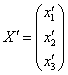. Систему, кстати, удобнее переписать в виде уже знакомого матричного уравнения:
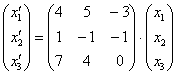или, если короче: .

Данный оператор определённым образом преобразует все векторы (а значит и точки) пространства. Геометрически это означает, что кот Леопольд, оказывается, например, сплющенным (не знаю, не проверял).

Теперь ВНИМАТЕЛЬНО записываем матрицу второго преобразования: 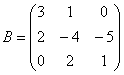(здесь существует немалый риск поставить ноль не там где нужно). Данное преобразование переводит векторы 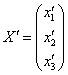в образы 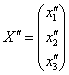, в результате чего «сплющенный кот», скажем, растягивается вдоль какой-нибудь плоскости.

Аналогично – запишем преобразование в матричном виде:
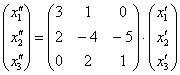или:

По условию, нужно найти результирующее (композиционное) преобразование, которое нам сразу даст «сплющенного и растянутого Леопольда». Подставим в уравнение :

Всё оказалось до безобразия просто – главное, матрицы перемножить в правильном порядке. Вычислим матрицу композиционного преобразования:

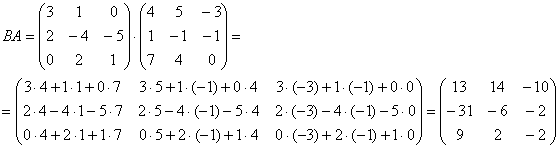
Если вы позабыли само матричное умножение, обратитесь к статье Свойства матричных операций, где я подробнейшим образом разобрал этот случай.

В результате:

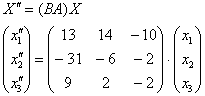
Осуществим матричное умножение в правой части:

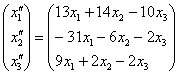
Две матрицы равны, если равны их соответствующие элементы. Таким образом, итоговое преобразование, выражающее координаты векторов-образов через координаты векторов-прообразов, запишется в виде следующей системы:

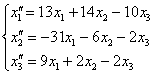
Выполним проверку. Для этого подставим уравнения , левой системы (см. условие) в правую часть каждого уравнения 2-й системы:

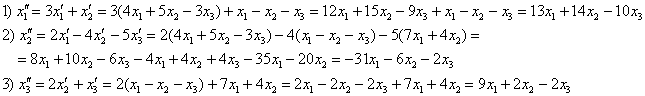
Что и требовалось проверить.

Этот способ, кстати, можно было бы рискнуть взять и за основной, если бы итоговое преобразование не требовалось найти средствами матричного исчисления

Ответ: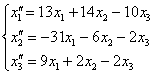

Как пользоваться этой системой? Очень просто – берём например, вектор 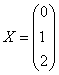и тупо подставляем его координаты:
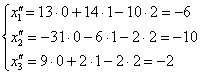– таким образом, он превратился в вектор .

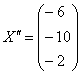Более академичный способ – использование матричного уравнения .

Энтузиасты могут смоделировать деформацию кота Леопольда с помощью специализированного программного обеспечения и отправить мне картинку, которую я обязательно опубликую. Мне и самому интересно, что же там с ним на самом деле произошло =) И такой энтузиаст нашёлся! – Леопольд,… выходи в 3d 8^)! Он и в самом деле оказался довольно сильно «сплюснутым и растянутым». Модель реализована в среде Wolfram Mathematica, вот картинка с другого ракурса, и это, к слову, уже дополнительное линейное преобразование. Выражаю особую благодарность всем, кто присылает свои решения, на сайте есть немало творческих задач и предложений, порой, даже жестоких :)

В том случае, если нужно «вернуть кота к первоначальному виду», следует найти обратную матрицу результирующего преобразования и воспользоваться уравнением .

«Плоский» случай для самостоятельного решения:

Пример 4

Даны два линейных преобразования в некотором базисе:

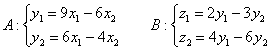
Найти образ вектора двумя способами:

1) путём последовательного применения преобразований и ;
2) с помощью композиционного оператора, выражающего координаты через .

Был велик соблазн вас запутать, но всё же я воздержался. Однако на практике нужно иметь в виду следующее:

– системы запросто могут быть переставлены местами;

– условие задачи может требовать выразить через и тогда потребуется дополнительно находить обратную матрицу результирующего преобразования;

В этой связи очень важно РАЗОБРАТЬСЯ в сути задания, и если что-то осталось недопонятым, обязательно перечитайте объяснения ещё раз – не лишним будет даже порисовать.

А сейчас переходим к вопросу, который назревал в течение всего урока:

Матрица линейного преобразования в различных базисах

В начале статьи мы выяснили происхождение матрицы линейного преобразования на примере оператора и ортонормированного базиса . Напоминаю: для того, чтобы записать матрицу линейного оператора в каком-либо базисе, нужно строго по порядку подействовать этим оператором на базисные векторы и полученные координаты занести в столбцы матрицы (слева направо). В результате «обработки» векторов нами была составлена матрица данного линейного преобразования в данном базисе.

Но ведь на «школьном» базисе свет клином не сошёлся! Ничто нам не мешает перейти к произвольному базису , где это же линейное преобразование, скорее всего, выразится другой матрицей. Но сам-то оператор не изменится – он будет по-прежнему увеличивать векторы плоскости в 2 раза. Таким образом, справедливо следующее утверждение, которое по существу уже было озвучено ранее:

одно и то же линейное преобразование в разных базисах в общем случае имеет РАЗНЫЕ матрицы.

И следующие две задачи как раз посвящены этому вопросу:

Пример 5

В базисе задано линейное преобразование . Найти матрицу данного преобразования в базисе , если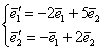

Решение: в условии задачи опять ничего не сказано о характере векторов, но для наглядности предположим, что данные базисы являются аффинными базисами плоскости. Как заметили внимательные читатели, предложенное линейное преобразование вытягивает все ненулевые объекты плоскости в направлении координатного вектора в 2 раза, и наша задача состоит в том, чтобы записать матрицу этого же преобразования в новом базисе . Для решения этого вопроса существует специальная формула:

, где – матрица перехода от базиса к базису .

Составляется она просто: берём вектор и «укладываем» коэффициенты его разложения (внимание!) в 1-й столбец матрицы: . Затем рассматриваем вектор и заносим коэффициенты его разложения во 2-й столбец:

Внимание! Базисные векторы, в данном случае векторы , следует «перебирать» строго по порядку!

Остальное дело техники. Находим обратную матрицу:

Произведение:

И, наконец, матрицу рассматриваемого линейного преобразования в новом базисе:

Пользуясь ассоциативностью матричного умножения, можно было сначала найти , а затем , но, в общем-то, это уже несущественные детали.

Ответ:

Ещё раз повторим смысл задания: само линейное преобразование не поменялось – оно по-прежнему растягивает ненулевые объекты плоскости вдоль «старого» вектора в 2 раза и не деформирует их в направлении вектора , но в новом базисе матрица данного преобразования уже другая. И вы видите её в ответе.

Очевидно, что найденная матрица задаёт обратное преобразование, т. е. выражает старые базисные векторы через новые. Аккуратно «транспонируем» столбцы матрицы в коэффициенты соответствующей системы: 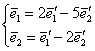. Таким образом, при желании всегда можно вернуться к старому базису: . Обратная формула следует из простых логических соображений, но её можно вывести и формально – разрешив матричное уравнение относительно .

Иногда матрицы и называют подобными.

Какой базис удобнее? Ну конечно, исходный , где матрица преобразования имеет вид , и сразу виднА характерная особенность этого преобразования. А что это за такой интересный базис, и как отыскать эту матрицу, вы узнаете на уроке о собственных векторах.

Трехмерный случай для самостоятельного решения:

Пример 6

Найти матрицу линейного преобразования в базисе , где , , , если она задана в базисе .

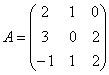
Пожалуйста, не путайте это задание с Примером № 3 – по первой оглядке здесь тоже какие-то похожие равенства, тоже штрихи, но смысл совершено другой. Если там шла речь о двух линейных преобразованиях и взаимосвязи координат векторов, то здесь – об одном и том же преобразовании и взаимосвязи векторов двух базисов.

Краткое решение и ответ совсем рядом.

И в завершении урока вернёмся к двумерному случаю и матрицам «два на два». Казалось бы, с геометрической точки зрения эти матрицы задают линейные преобразования плоскости и разговор закончен. Но на самом деле это не так – у матриц есть и другой геометрический смысл, с которым можно ознакомиться на уроке Переход к новому базису. Сначала я хотел включить пару соответствующих примеров в эту статью, но чуть позже решил, что материал будет уместнее опубликовать в разделе аналитической геометрии.

Ну и конечно, не забываем, что рассматриваемый материал касается не только геометрических векторов плоскости и пространства, но и вообще любых векторов.

Спасибо за внимание, жду вас на следующем, не менее увлекательном уроке о собственных числах и собственных векторах линейного преобразования.

Решения и ответы:

Пример 2 Решение: найдём матрицу обратного преобразования:
(см. урок. Как найти обратную матрицу)
Найдём прообразы:

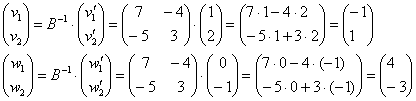
Ответ:

Пример 4. Решение: запишем матрицы преобразований:

1) Последовательно применим к вектору преобразования и :

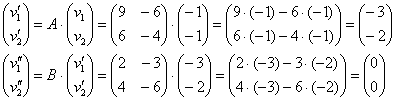
2) Найдём результирующее преобразование:

Таким образом:

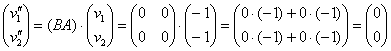
Ответ: (нулевой вектор)

Пример 6. Решение: используем формулу . Запишем матрицу перехода к новому базису:

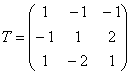
Найдём матрицу обратного перехода:

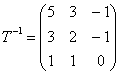
Вычислим:

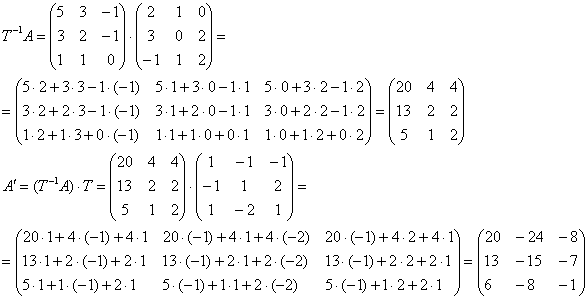
Ответ: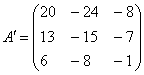

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?