Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Формула полной вероятности и формулы Байеса

На данном уроке мы рассмотрим важное следствие теорем сложения и умножения вероятностей и научимся решать типовые задачи по теме. Читателям, которые ознакомились со статьёй о зависимых событиях, будет проще, поскольку в ней мы уже по факту начали использовать формулу полной вероятности. Если Вы зашли с поисковика и/или неважно разбираетесь в теории вероятностей (ссылка на 1-й урок курса), то сначала рекомендую посетить указанные страницы.

Собственно, продолжаем. Рассмотрим зависимое событие , которое может произойти лишь в результате осуществления одной из несовместных гипотез , которые образуют полную группу. Пусть известны их вероятности  и соответствующие условные вероятности . Тогда вероятность наступления события  равна:

Эта формула получила название формулы полной вероятности. В учебниках она формулируется теоремой, доказательство которой элементарно: согласно алгебре событий,  (произошло событие  и после него наступило событие  или произошло событие  и после него наступило событие  или произошло событие  и после него наступило событие  или …. или произошло событие  и после него наступило событие ). Поскольку гипотезы  несовместны, а событие  – зависимо, то по теореме сложения вероятностей несовместных событий (первый шаг) и теореме умножения вероятностей зависимых событий (второй шаг):

Наверное, многие предчувствуют содержание первого примера =)

Куда ни плюнь – везде урна:

Задача 1

Имеются три одинаковые урны. В первой урне находятся 4 белых и 7 черных шаров, во второй – только белые и в третьей – только черные шары. Наудачу выбирается одна урна и из неё наугад извлекается шар. Какова вероятность того, что этот шар чёрный?

Решение: рассмотрим событие  – из наугад выбранной урны будет извлечён чёрный шар.  Данное событие может произойти или не произойти в результате осуществления одной из следующих гипотез:
 – будет выбрана 1-я урна;
 – будет выбрана 2-я урна;
 – будет выбрана 3-я урна.

Так как урна выбирается наугад, то выбор любой из трёх урн равновозможен, следовательно:

Обратите внимание, что перечисленные гипотезы образуют полную группу событий, то есть, по условию чёрный шар может появиться только из этих урн, а например, не прилететь с бильярдного стола. Проведём простую промежуточную проверку:
, ОК, едем дальше:

В первой урне 4 белых + 7 черных = 11 шаров, по классическому определению:
 – вероятность извлечения чёрного шара при условии, что будет выбрана 1-я урна.

Во второй урне только белые шары, поэтому в случае её выбора появление чёрного шара становится невозможным: .

И, наконец, в третьей урне одни чёрные шары, а значит, соответствующая условная вероятность извлечения чёрного шара составит  (событие достоверно).

По формуле полной вероятности:

 – вероятность того, что из наугад выбранной урны будет извлечен чёрный шар.

Ответ:

Разобранный пример снова наводит на мысль о том, как важно ВНИКАТЬ В УСЛОВИЕ. Возьмём те же задачи с урнами и шарами – при их внешней схожести способы решения могут быть совершенно разными: где-то требуется применить только классическое определение вероятности, где-то события независимы, где-то зависимы, а где-то речь о гипотезах. При этом не существует чёткого формального критерия для выбора пути решения – над ним почти всегда нужно думать. Как повысить свою квалификацию? Решаем, решаем и ещё раз решаем!

Задача 2

В тире имеются 5 различных по точности боя винтовок. Вероятности попада­ния в мишень для данного стрелка соответственно равны 0,5; 0,55; 0,7; 0,75 и 0,4. Чему равна вероятность попадания в мишень, если стрелок делает один выстрел из слу­чайно выбранной винтовки?

Краткое решение и ответ в конце урока.

В большинстве тематических задач гипотезы, конечно же, не равновероятны:

Задача 3

В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок производит один выстрел из наудачу взятой винтовки.

Решение: в этой задаче количество винтовок точно такое же, как и в предыдущей, но вот гипотезы всего две:
 – стрелок выберет винтовку с оптическим прицелом;
 – стрелок выберет винтовку без оптического прицела.
По классическому определению вероятности: .
Контроль:

Рассмотрим событие:  – стрелок поразит мишень из наугад взятой винтовки.
По условию: .

По формуле полной вероятности:

Ответ: 0,85

На практике вполне допустим укороченный способ оформления задачи, который вам тоже хорошо знаком:

Решение: по классическому определению:   – вероятности  выбора винтовки с оптическим и без оптического прицела соответственно.

По условию,  – вероятности попадания в мишень из соответствующих типов винтовок.

По формуле полной вероятности:
 – вероятность того, что стрелок поразит мишень из наугад выбранной винтовки.

Ответ: 0,85

Следующая задача для самостоятельного решения:

Задача 4

Двигатель работает в трёх режимах: нормальном, форсированном и на холостом ходу. В режиме холостого хода вероятность его выхода из строя равна 0,05, при нормальном режиме работы – 0,1, а при форсированном – 0,7. 70% времени двигатель работает в нормальном режиме, а 20% – в форсированном. Какова вероятность выхода из строя двигателя во время работы?

На всякий случай напомню – чтобы получить значения вероятностей проценты нужно разделить на 100. Будьте очень внимательны! По моим наблюдениям, условия задач на формулу полной вероятности частенько пытаются подзапутать; и я специально подобрал такой пример. Скажу по секрету – сам чуть не запутался =)

Решение в конце урока (оформлено коротким способом)

Задачи на формулы Байеса

Материал тесно связан с содержанием предыдущего параграфа. Пусть событие  наступило в результате осуществления одной из гипотез .  Как определить вероятность того, что имела место та или иная гипотеза?

При условии, что событие  уже произошло, вероятности гипотез переоцениваются по формулам, которые получили фамилию английского священника Томаса Байеса:

 – вероятность того, что имела место гипотеза ;
 – вероятность того, что имела место гипотеза ;
 – вероятность того, что имела место гипотеза ;
…
 – вероятность того, что имела место гипотеза .

На первый взгляд кажется полной нелепицей – зачем пересчитывать вероятности гипотез, если они и так известны? Но на самом деле разница есть:

 – это априорные (оцененные до испытания) вероятности.

 – это апостериорные (оцененные после испытания) вероятности тех же гипотез, пересчитанные в связи «со вновь открывшимися обстоятельствами » – с учётом того факта, что событие  достоверно произошло.

Рассмотрим это различие на конкретном примере:

Задача 5

На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии составляет 20%, а во второй – 10%. Наудачу взятое со склада изделие оказалось стандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии.

Первая часть решения состоит в использовании формулы полной вероятности. Иными словами, вычисления проводятся в предположении, что испытание ещё не произведено и событие «изделие оказалось стандартным» пока не наступило.

Рассмотрим две гипотезы:
 – наудачу взятое изделие будет из 1-й партии;
 – наудачу взятое изделие будет из 2-й партии.

Всего: 4000 + 6000 = 10000 изделий на складе. По классическому определению:
.

Контроль:  

Рассмотрим зависимое событие:  – наудачу взятое со склада изделие будет стандартным.

В первой партии 100% – 20% = 80% стандартных изделий, поэтому:  – вероятность того, что наудачу взятое на складе изделие будет стандартным при условии, что оно принадлежит 1-й партии.

Аналогично, во второй партии 100% – 10% = 90% стандартных изделий и  – вероятность того, что наудачу взятое на складе изделие будет стандартным при условии, что оно принадлежит 2-й партии.

По формуле полной вероятности:
 – вероятность того, что наудачу взятое на складе изделие будет стандартным.

Часть вторая. Пусть наудачу взятое со склада изделие оказалось стандартным. Эта фраза прямо прописана в условии, и она констатирует тот факт, что событие  произошло.

По формулам Байеса:

а)  – вероятность того, что выбранное стандартное изделие принадлежит 1-й партии;

б)  – вероятность того, что выбранное стандартное изделие принадлежит 2-й партии.

После переоценки гипотезы , разумеется, по-прежнему образуют полную группу:
 (проверка ;-))

Ответ:

Понять смысл переоценки гипотез нам поможет Иван Васильевич, которой снова сменил профессию и стал директором завода. Он знает, что сегодня 1-й цех отгрузил на склад 4000, а 2-й цех – 6000 изделий, и приходит удостовериться в этом. Предположим, вся продукция однотипна и находится в одном контейнере. Естественно, Иван Васильевич предварительно подсчитал, что изделие, которое он сейчас извлечёт для проверки, с вероятностью  будет выпущено 1-м цехом и с вероятностью  – вторым. Но после того как выбранное изделие оказывается стандартным, он восклицает: «Какой же классный болт! – его скорее выпустил 2-й цех». Таким образом, вероятность второй гипотезы переоценивается в лучшую сторону , а вероятность первой гипотезы занижается: . И эта переоценка небезосновательна – ведь 2-й цех произвёл не только больше изделий, но и работает в 2 раза лучше!

Вы скажете, чистый субъективизм? Отчасти – да, более того, сам Байес интерпретировал апостериорные вероятности как уровень доверия. Однако не всё так просто – в байесовском подходе есть и объективное зерно. Ведь вероятности того, что изделие будет стандартным (0,8 и 0,9 для 1-го и 2-го цехов соответственно) это предварительные (априорные) и средние оценки. Но, выражаясь философски – всё течёт, всё меняется, и вероятности в том числе. Вполне возможно, что на момент исследования более успешный 2-й цех повысил процент выпуска стандартных изделий (и/или 1-й цех снизил), и если проверить бОльшее количество либо все 10 тысяч изделий на складе, то переоцененные значения  окажутся гораздо ближе к истине.

Кстати, если Иван Васильевич извлечёт нестандартную деталь, то наоборот – он будет больше «подозревать» 1-й цех и меньше – второй. Предлагаю убедиться в этом самостоятельно:

Задача 6

На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии 20%, во второй – 10%. Наудачу взятое со склада изделие оказалось нестандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии.

Условие отличатся двумя буквами, которые я выделил жирным шрифтом. Задачу можно решить с «чистого листа», или воспользоваться результатами предыдущих вычислений. В образце я провёл полное решение, но чтобы не возникло формальной накладки с Задачей № 5, событие «наудачу взятое со склада изделие будет нестандартным» обозначено через .

Байесовская схема переоценки вероятностей встречается повсеместно, причём её активно эксплуатируют и различного рода мошенники. Рассмотрим ставшее нарицательным АО на три буквы, которое привлекает вклады населения, якобы куда-то их инвестирует, исправно выплачивает дивиденды и т.д. Что происходит? Проходит день за днём, месяц за месяцем и всё новые и новые факты, донесённые путём рекламы и «сарафанным радио», только повышают уровень доверия к финансовой пирамиде (апостериорная байесовская переоценка в связи с произошедшими событиями!). То есть, в глазах вкладчиков происходит постоянное увеличение вероятности того, что «это серьёзная контора»; при этом вероятность противоположной гипотезы («это очередные кидалы»), само собой, уменьшается и уменьшается. Дальнейшее, думаю, понятно. Примечательно, что заработанная репутация даёт организаторам время успешно скрыться от Ивана Васильевича, который остался не только без партии болтов, но и без штанов.

К не менее любопытным примерам мы вернёмся чуть позже, а пока на очереди, пожалуй, самый распространенный случай с тремя гипотезами:  

Задача 7

Электролампы изготавливаются на трех заводах. 1-й завод производит 30% общего количества ламп, 2-й – 55%, а 3-й – остальную часть. Продукция 1-го завода содержит 1% бракованных ламп, 2-го – 1,5%, 3-го – 2%. В магазин поступает продукция всех трех заводов. Купленная лампа оказалась с браком. Какова вероятность того, что она произведена 2-м заводом?

Заметьте, что в задачах на формулы Байеса в условии обязательно фигурирует некое произошедшее событие, в данном случае – покупка лампы.

Событий прибавилось, и решение удобнее оформить в «быстром» стиле.

Алгоритм точно такой же: на первом шаге находим вероятность того, что купленная лампа вообще окажется бракованной.

Пользуясь исходными данными, переводим проценты в вероятности:
 – вероятности того, что лампа произведена 1-м, 2-м и 3-м заводами соответственно.
Контроль:

Аналогично:  – вероятности изготовления бракованной лампы для соответствующих заводов.

По формуле полной вероятности:

 – вероятность того, что купленная лампа окажется с браком.

Шаг второй. Пусть купленная лампа оказалась бракованной (событие произошло)

По формуле Байеса:
 – вероятность того, что купленная бракованная лампа изготовлена вторым заводом

Ответ:

Почему изначальная вероятность 2-й гипотезы  после переоценки увеличилась ? Ведь второй завод производит средние по качеству лампы (первый – лучше, третий – хуже). Так почему же возросла апостериорная вероятность, что бракованная лампа именно со 2-го завода? Это объясняется уже не «репутацией», а размером. Так как завод № 2 выпустил самое большое количество ламп, то на него (по меньшей мере, субъективно) и пеняют: «скорее всего, эта бракованная лампа именно оттуда».

Интересно заметить, что вероятности 1-й и 3-й гипотез, переоценились в ожидаемых направлениях и сравнялись:

Контроль: , что и требовалось проверить.

К слову, о заниженных и завышенных оценках:

Задача 8

В студенческой группе 3 человека имеют высокий уровень подготовки, 19 человек – средний и 3 – низкий. Вероятности успешной сдачи экзамена для данных студентов соответственно равны: 0,95; 0,7 и 0,4. Известно, что некоторый студент сдал экзамен. Какова вероятность того, что:

а) он был подготовлен очень хорошо;
б) был подготовлен средне;
в) был подготовлен плохо.

Проведите вычисления и проанализируйте результаты переоценки гипотез.

Задача приближена к реальности и особенно правдоподобна для группы студентов-заочников, где преподаватель практически не знает способностей того или иного студента. При этом результат может послужить причиной довольно-таки неожиданных последствий (особенно это касается экзаменов в 1-м семестре). Если плохо подготовленному студенту посчастливилось с билетом, то преподаватель с большой вероятностью сочтёт его хорошо успевающим или даже сильным студентом, что принесёт неплохие дивиденды в будущем (естественно, нужно «поднимать планку» и поддерживать свой имидж). Если же студент 7 дней и 7 ночей учил, зубрил, повторял, но ему просто не повезло, то дальнейшие события могут развиваться в самом скверном ключе – с многочисленными пересдачами и балансировкой на грани вылета.

Что и говорить, репутация – это важнейший капитал, не случайно многие корпорации носят имена-фамилии своих отцов-основателей, которые руководили делом 100-200 лет назад и прославились своей безупречной репутацией.

Да, байесовский подход в известной степени субъективен, но… так устроена жизнь!

Закрепим материал заключительным индустриальным примером, в котором я расскажу о до сих пор не встречавшихся технических тонкостях решения:

Задача 9

Три цеха завода производят однотипные детали, которые поступают на сборку в общий контейнер. Известно, что первый цех производит в 2 раза больше деталей, чем второй цех, и в 4 раза больше третьего цеха. В первом цехе брак составляет 12%, во втором – 8%, в третьем – 4%. Для контроля из контейнера берется одна деталь. Какова вероятность того, что она окажется бракованной? Какова вероятность того, что извлечённую бракованную деталь выпустил 3-й цех?

Таки Иван Васильевич снова на коне =) Должен же быть у фильма счастливый конец =)

Решение: в отличие от Задач № 5-8 здесь в явном виде задан вопрос, который разрешается с помощью формулы полной вероятности. Но с другой стороны, условие немного «зашифровано», и разгадать этот ребус нам поможет школьный навык составлять простейшие уравнения. За «икс» удобно принять наименьшее значение:

Пусть  – доля деталей, выпускаемая третьим цехом.

По условию, первый цех производит в 4 раза больше третьего цеха, поэтому доля 1-го цеха составляет .

Кроме того, первый цех производит изделий в 2 раза больше, чем второй цех, а значит, доля последнего: .

Составим и решим уравнение:

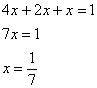
Таким образом:  – вероятности того, что извлечённая из контейнера деталь выпущена 1-м, 2-м и 3-м цехами соответственно.

Контроль: . Кроме того, будет не лишним ещё раз посмотреть на фразу «Известно, что первый цех производит изделий в 2 раза больше второго цеха и в 4 раза больше третьего цеха» и убедиться, что полученные значения вероятностей действительно соответствуют этому условию.

За «икс» изначально можно было принять долю 1-го либо долю 2-го цеха – вероятности выйдут такими же. Но, так или иначе, самый трудный участок пройден, и решение входит в накатанную колею:

Из условия находим:
 – вероятности изготовления бракованной детали для соответствующих цехов.

По формуле полной вероятности:
 – вероятность того, что наугад извлеченная из контейнера деталь окажется бракованной.

Вопрос второй: какова вероятность того, что извлечённую бракованную деталь выпустил 3-й цех? Данный вопрос предполагает, что деталь уже извлечена, и она оказалось бракованной. Переоцениваем гипотезу по формуле Байеса:
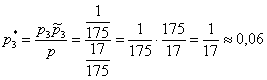 – искомая вероятность. Совершенно ожидаемо – ведь третий цех производит не только самую малую долю деталей, но и лидирует по качеству!

В данном случае пришлось упрощать четырёхэтажную дробь, что в задачах на формулы Байеса приходится делать довольно часто. Но для данного урока я как-то так случайно подобрал примеры, в которых многие вычисления можно провести без обыкновенных дробей.

Коль скоро в условии нет пунктов «а» и «бэ», то ответ лучше снабдить текстовыми комментариями:

Ответ:  – вероятность того, что извлечённая из контейнера деталь окажется бракованной;  – вероятность того, что извлечённую бракованную деталь выпустил 3-й цех.

Как видите, задачи на формулу полной вероятности и формулы Байеса достаточно простЫ, и, наверное, по этой причине в них так часто пытаются затруднить условие, о чём я уже упоминал в начале статьи.

Дополнительные примеры есть в файле с готовыми решениями на Ф.П.В. и формулы Байеса, кроме того, наверное, найдутся желающие более глубоко ознакомиться с данной темой в других источниках. А тема действительно очень интересная – чего только стОит один парадокс Байеса, который обосновывает тот житейский совет, что если у человека диагностирована редкая болезнь, то ему имеет смысл провести повторное и даже два повторных независимых обследования. Казалось бы, это делают исключительно от отчаяния… – а вот и нет! Но не будем о грустном.

Везения в главном!

Решения и ответы:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте