


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Производная функции, заданной неявно.
Производная параметрически заданной функции
В данной статье мы рассмотрим ещё два типовых задания, которые часто встречаются в контрольных работах по высшей математике. Для того чтобы успешно освоить материал, необходимо уметь находить производные хотя бы на среднем уровне. Научиться находить производные практически с нуля можно на двух базовых уроках Как найти производную? Примеры решений и Производная сложной функции. Если с навыками дифференцирования всё в порядке, тогда поехали.
Производная функции, заданной неявно
Или короче – производная неявной функции. Что такое неявная функция? Давайте сначала вспомним само определение функции одной переменной:
функция одной переменной ![]() – это правило, по которому каждому значению независимой переменной
– это правило, по которому каждому значению независимой переменной ![]() соответствует одно и только одно значение функции
соответствует одно и только одно значение функции ![]() .
.
Переменная ![]() называется независимой переменной или аргументом.
называется независимой переменной или аргументом.
Переменная ![]() называется зависимой переменной или функцией.
называется зависимой переменной или функцией.
До сих пор мы рассматривали функции, заданные в явном виде. Что это значит? Устроим разбор полётов на конкретных примерах.
Рассмотрим функцию ![]()
Здесь слева у нас одинокий «игрек», а справа – только «иксы» (ну и, понятно, числа, знаки). То есть функция ![]() в явном виде выражена через независимую переменную
в явном виде выражена через независимую переменную ![]() .
.
Рассмотрим другую функцию: ![]()
Тут переменные ![]() и
и ![]() расположены «вперемешку». Причем никакими алгебраическими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др. Перепишите равенство
расположены «вперемешку». Причем никакими алгебраическими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др. Перепишите равенство ![]() и попробуйте выразить «игрек» в явном виде:
и попробуйте выразить «игрек» в явном виде: ![]() . Можно крутить-вертеть уравнение часами, но у вас этого не получится.
. Можно крутить-вертеть уравнение часами, но у вас этого не получится.
Разрешите познакомить: ![]() – пример неявной функции.
– пример неявной функции.
В курсе математического анализа доказано, что неявная функция существует (однако не всегда), у неё есть график (точно так же, как и у «нормальной» функции). У неявной функции точно так же существует первая производная, вторая производная и т. д. Как говорится, все права секс-меньшинств соблюдены.
И на этом уроке мы научимся находить производную функции, которая задана неявно. Это не так сложно! Все правила дифференцирования, таблица производных элементарных функций остаются в силе. Разница будет в одном своеобразном моменте, который мы рассмотрим прямо сейчас.
Да, и сообщу хорошую новость – рассмотренные ниже задания выполняются по довольно жесткому и чёткому алгоритму без камня перед тремя дорожками.
Пример 1
Найти производную функции, заданной неявно ![]()
1) На первом этапе навешиваем штрихи на обе части:
![]()
2) Используем свойство линейности производной (первые два правила урока Как найти производную? Примеры решений):
![]()
3) Непосредственное дифференцирование.
Как дифференцировать ![]() и
и ![]() совершенно понятно. Что делать там, где под штрихами есть «игреки»?
совершенно понятно. Что делать там, где под штрихами есть «игреки»?
![]() – просто до безобразия, производная от функции равна её производной:
– просто до безобразия, производная от функции равна её производной: ![]() .
.
Как дифференцировать ![]()
Здесь у нас сложная функция. Почему? Вроде бы под синусом всего одна буква «игрек». Но, дело в том, что всего одна буква «игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (см. определение в начале урока). Таким образом, синус – внешняя функция, ![]() – внутренняя функция. Используем правило дифференцирования сложной функции
– внутренняя функция. Используем правило дифференцирования сложной функции ![]() . Согласно таблице производных, синус превращается в косинус, только вместо «икс» у нас буковка «игрек»:
. Согласно таблице производных, синус превращается в косинус, только вместо «икс» у нас буковка «игрек»:
![]()
Произведение дифференцируем по формуле ![]() :
:
![]()
Обратите внимание, что ![]() – тоже сложная функция, любой «игрек с наворотами» – сложная функция:
– тоже сложная функция, любой «игрек с наворотами» – сложная функция:
![]()
Само оформление решения должно выглядеть примерно так:
![]()
![]()
если есть скобки, то раскрываем их:
![]()
4) В левой части собираем слагаемые, в которых есть «игрек штрих». В правую часть – переносим всё остальное:
![]()
5) В левой части выносим производную ![]() за скобки:
за скобки:
![]()
6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:
![]()
Производная найдена. Готово.
Интересно отметить, что в неявном виде можно записать и «обычную» функцию. Например, функцию ![]() можно переписать так:
можно переписать так: ![]() . И продифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная,
. И продифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная, ![]() – эта функция задана в неявном виде, но здесь можно выразить «игрек» и представить функцию в явном виде. Под словами же «неявная функция» чаще понимают «классическую» неявную функцию, когда «игрек» выразить нельзя.
– эта функция задана в неявном виде, но здесь можно выразить «игрек» и представить функцию в явном виде. Под словами же «неявная функция» чаще понимают «классическую» неявную функцию, когда «игрек» выразить нельзя.
Ещё более общее название – это неявное уравнение, которое может неявно задавать сразу две или даже бОльшее количество функций, так, например, уравнение окружности ![]() неявно задаёт функции
неявно задаёт функции ![]() ,
, ![]() , которые определяют полуокружности. Но, в рамках данной статьи, мы не будем делать особого различия между терминами и нюансами, это была просто информация для общего развития.
, которые определяют полуокружности. Но, в рамках данной статьи, мы не будем делать особого различия между терминами и нюансами, это была просто информация для общего развития.
Второй способ решения
Внимание! Со вторым способом можно ознакомиться только в том случае, если Вы умеете уверенно находить частные производные. Начинающие изучать математический анализ и чайники, пожалуйста, не читайте и пропустите этот пункт, иначе в голове будет полная каша.
Найдем производную неявной функции ![]() вторым способом.
вторым способом.
Переносим все слагаемые в левую часть:
![]()
И рассматриваем функцию двух переменных:
![]()
Тогда нашу производную можно найти по формуле ![]()
Найдем частные производные:
![]()
![]()
Таким образом:
![]()
Второй способ решения позволяет выполнить проверку. Но оформлять им чистовой вариант задания нежелательно, поскольку частные производные осваивают позже, и студент, изучающий тему «Производная функции одной переменной», знать частные производные как бы еще не должен.
Рассмотрим еще несколько примеров.
Пример 2
Найти производную функции, заданной неявно ![]()
Навешиваем штрихи на обе части:
![]()
Используем правила линейности:
![]()
Находим производные:
![]()
![]()
Раскрываем все скобки:
![]()
Собираем все слагаемые с ![]() в левой части, остальные – в правой:
в левой части, остальные – в правой:
![]()
В левой части выносим ![]() за скобку:
за скобку:
![]()
Окончательный ответ:
![]()
Пример 3
Найти производную функции, заданной неявно ![]()
Полное решение и образец оформления в конце урока.
Не редкость, когда после дифференцирования приходится иметь дело с дробями. В таких случаях от дробей нужно избавляться. Рассмотрим ещё два примера.
Пример 4
Найти производную функции, заданной неявно ![]()
Заключаем обе части под штрихи и слева используем правило суммы:
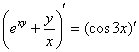
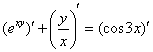
Дифференцируем, используя правило дифференцирования сложной функции ![]() и правило дифференцирования частного
и правило дифференцирования частного 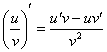 :
:
![]()
![]()
![]()
Раскрываем скобки:
![]()
Теперь нам нужно избавиться от дроби. Это можно сделать и позже, но рациональнее сделать сразу же. В знаменателе дроби находится ![]() . Умножаем каждое слагаемое каждой части на
. Умножаем каждое слагаемое каждой части на ![]() . Если подробно, то выглядеть это будет так:
. Если подробно, то выглядеть это будет так:
![]()
![]()
Иногда после дифференцирования появляется 2-3 дроби. Если бы у нас была еще одна дробь, например, ![]() , то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на
, то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на ![]()
Далее алгоритм работает стандартно, после того, как все скобки раскрыты, все дроби устранены, слагаемые, где есть «игрек штрих» собираем в левой части, а в правую часть помещаем всё остальное:
![]()
В левой части выносим ![]() за скобку:
за скобку:
![]()
Окончательный ответ:
![]()
Пример 5
Найти производную функции, заданной неявно ![]()
Это пример для самостоятельного решения. Единственное, в нём, перед тем как избавиться от дроби, предварительно удобно избавиться от трёхэтажности самой дроби. Полное решение и ответ в конце урока.
О том, как найти производную 2-го, 3-го и более высоких порядков от неявно заданной функции, читайте в статье Производные высших порядков.
Производная параметрически заданной функции
Не напрягаемся, в этом параграфе тоже всё достаточно просто. Можно записать общую формулу параметрически заданной функции, но, для того, чтобы было понятно, я сразу запишу конкретный пример. В параметрической форме функция задаётся двумя уравнениями: ![]() . Частенько уравнения записывают не под фигурными скобками, а последовательно:
. Частенько уравнения записывают не под фигурными скобками, а последовательно: ![]() ,
, ![]() .
.
Переменная ![]() называется параметром и может принимать значения от «минус» бесконечности до «плюс» бесконечности. Рассмотрим, например, значение
называется параметром и может принимать значения от «минус» бесконечности до «плюс» бесконечности. Рассмотрим, например, значение ![]() и подставим его в оба уравнения:
и подставим его в оба уравнения: ![]() . Или по человечески: «если икс равен четырем, то игрек равно единице». На координатной плоскости можно отметить точку
. Или по человечески: «если икс равен четырем, то игрек равно единице». На координатной плоскости можно отметить точку ![]() , и эта точка будет соответствовать значению параметра
, и эта точка будет соответствовать значению параметра ![]() . Аналогично можно найти точку для любого значения параметра «тэ». Как и для «обычной» функции, для параметрически заданной функции все права тоже соблюдены: можно построить график, найти производные и т. д. Кстати, если есть надобность построить график параметрически заданной функции, можете воспользоваться моей программой.
. Аналогично можно найти точку для любого значения параметра «тэ». Как и для «обычной» функции, для параметрически заданной функции все права тоже соблюдены: можно построить график, найти производные и т. д. Кстати, если есть надобность построить график параметрически заданной функции, можете воспользоваться моей программой.
Как найти производную параметрически заданной функции? В простых случаях, как наш, есть возможность представить функцию в явном виде. Выразим из первого уравнения параметр: ![]() – и подставим его во второе уравнение:
– и подставим его во второе уравнение: ![]() . После чего дифференцируем по обычной схеме.
. После чего дифференцируем по обычной схеме.
В более «тяжелых» случаях такой фокус не прокатывает. Но это не беда, потому что для нахождения производной параметрической функции существует формула:
![]()
Находим производную от «игрека по переменной тэ»:
![]()
Все правила дифференцирования и таблица производных справедливы, естественно, и для буквы ![]() , таким образом, какой-то новизны в самом процессе нахождения производных нет. Просто мысленно замените в таблице все «иксы» на букву «тэ».
, таким образом, какой-то новизны в самом процессе нахождения производных нет. Просто мысленно замените в таблице все «иксы» на букву «тэ».
Находим производную от «икса по переменной тэ»:
![]()
Теперь только осталось подставить найденные производные в нашу формулу:
![]()
Готово. Производная, как и сама функция, тоже зависит от параметра ![]() .
.
Что касается обозначений, то в формуле вместо записи ![]() можно было просто записать
можно было просто записать ![]() без подстрочного индекса, поскольку это «обычная» производная «по икс». Но в литературе всегда встречается вариант
без подстрочного индекса, поскольку это «обычная» производная «по икс». Но в литературе всегда встречается вариант ![]() , поэтому я не буду отклоняться от стандарта.
, поэтому я не буду отклоняться от стандарта.
Пример 6
Найти производную функции, заданной параметрически 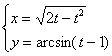
Используем формулу ![]()
В данном случае:
![]()
![]()
Таким образом:
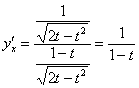
Особенностью нахождения производной параметрической функции является тот факт, что на каждом шаге результат выгодно максимально упрощать. Так, в рассмотренном примере при нахождении ![]() я раскрыл скобки под корнем (хотя мог этого и не делать). Велик шанс, что при подстановке
я раскрыл скобки под корнем (хотя мог этого и не делать). Велик шанс, что при подстановке ![]() и
и ![]() в формулу многие вещи хорошо сократятся. Хотя встречаются, конечно, примеры и с корявыми ответами.
в формулу многие вещи хорошо сократятся. Хотя встречаются, конечно, примеры и с корявыми ответами.
Пример 7
Найти производную функции, заданной параметрически 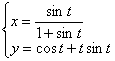
Это пример для самостоятельного решения.
В статье Простейшие типовые задачи с производной мы рассматривали примеры, в которых требовалось найти вторую производную функции. Для параметрически заданной функции тоже можно найти вторую производную, и находится она по следующей формуле: ![]() . Совершенно понятно, что для того чтобы найти вторую производную, нужно сначала найти первую производную.
. Совершенно понятно, что для того чтобы найти вторую производную, нужно сначала найти первую производную.
Пример 8
Найти первую и вторую производные функции, заданной параметрически 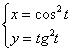
Сначала найдем первую производную.
Используем формулу ![]()
В данном случае:
![]()
![]()
Подставляем найденные производные в формулу. В целях упрощений используем тригонометрическую формулу ![]() :
:
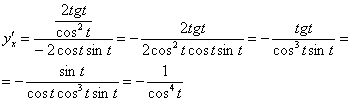
Я заметил, что в задаче на нахождение производной параметрической функции довольно часто в целях упрощений приходится использовать тригонометрические формулы. Помните их или держите под рукой, и не пропускайте возможность упростить каждый промежуточный результат и ответы. Зачем? Сейчас нам предстоит взять производную от ![]() , и это явно лучше, чем находить производную от
, и это явно лучше, чем находить производную от ![]() .
.
Найдем вторую производную.
Используем формулу: ![]() .
.
Посмотрим на нашу формулу. Знаменатель ![]() уже найден на предыдущем шаге. Осталось найти числитель – производную по переменной «тэ» от первой производной:
уже найден на предыдущем шаге. Осталось найти числитель – производную по переменной «тэ» от первой производной:
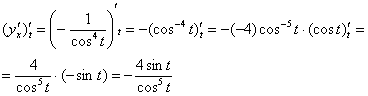
И по формуле:
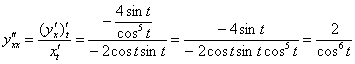
Готово.
Для закрепления материала предлагаю еще пару примеров для самостоятельного решения.
Пример 9
Найти ![]() и
и ![]() функции, заданной параметрически
функции, заданной параметрически 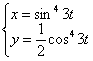
Пример 10
Найти ![]() и
и ![]() функции, заданной параметрически
функции, заданной параметрически 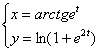
Надеюсь, это занятие было полезным, и Вы теперь с лёгкостью сможете находить производные, если функция задана неявно или параметрически.
Желаю успехов!
Решения и ответы:
Пример 3. Решение:
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом: ![]()
Пример 5. Решение:
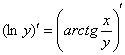
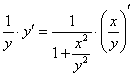
![]()
![]()
![]()
![]()
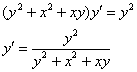
Пример 7. Решение: используем формулу ![]()
В данном случае:
![]()
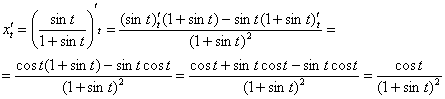
Таким образом:
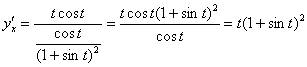
Пример 9. Решение: найдем первую производную.
Используем формулу: ![]() . В данном случае:
. В данном случае:
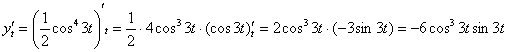
![]()
![]()
Вторую производную найдём по формуле ![]() .
.
![]()
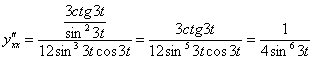
Пример 10. Решение: используем формулу: ![]() . В данном случае:
. В данном случае:
![]()
![]()
Таким образом:
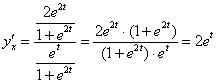
Вторая производная:
![]()
![]()
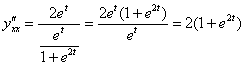
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright